基于系统生物学的白介素—6的建模信号转导模拟分析

齐云峰 孙添添 韩艳雪

[摘要]白介素-6，全名白细胞介素-6，是一种多功能细胞因子，能诱导细胞增殖分化。胞内受体和蛋白磷酸化调节在IL-6信号转导中起重大作用。在本研究中采用系统生物学建模工具COPASI，进行IL-6的建模信号转导模拟分析。通过扰动pp2初始浓度，发现pp2对IL-6信号转导有抑制作用呈负相关。通过扰动gp130初始浓度，发现受体gp130与IL-6的信号转导弱正相关。通过协同扰动受体gp130与pp2初始浓度，发现对于IL-6的信号转导来说最适宜的受体浓度为模型初始浓度，而pp2浓度升高抑制IL-6的信号转导。

[关键词]白介素-6 数学模拟 糖蛋白130 信号转导

[中图分类号]Q94 [文献标识码]A [文章编号]1009-5349（2016）16-0154-02

随着系统生物学不断发展，系统生物学研究思想得到了学术界的广泛认同，系统生物学将成为21世纪医学和生物学的核心驱动力。[1-2]系统生物学重要性主要有两个方面：（1）基因组学与蛋白质组学中的高通量方法为系统生物学的发展提供了大量的数据，系统生物学能整合分析这些数据。（2）计算生物学包含数据处理、模型构建和理论分析，是系统生物学发展过程中的一个重要的工具。[3]

IL-6是由184个氨基酸组成，有2条糖蛋白链。1条为糖蛋白80，另1条为gp130。[4]gp80只能以低亲合性与IL-6结合，所形成的复合物迅速与高亲和性的gp130结合，通过此链传递信息。蛋白磷酸酶1和蛋白磷酸酶2作为JAK/STAT通路内两种磷酸酶，分别在细胞质和细胞核中催化STAT1*和STAT3*的去磷酸化作用。蛋白磷酸酶1和蛋白磷酸酶2的蛋白的总量是固定不变的，并且只有蛋白单体才能与新形成的STAT*结合以完成去磷酸化作用。

IL-6可以作为在免疫应答中产生重要介质的一种机体，具有多种生物学活性。一方面它具有能调节功能，其中包括细胞增殖、免疫防御机制及血细胞生成等，[5]另一方面它还能通过干预细胞的黏附性和活动力、血栓形成、及肿瘤细胞的增殖，而影响肿瘤的进展。随着系统生物学的发展，IL-6的信号转导机制在医学上的应用更为广泛，在许多疾病中发现其重要作用。例如心血管疾病[6]、自身免疫疾病、肿瘤[7-8]等。此外，随着研究者对IL-6的信号转导的研究深入，构建了一系列的IL-6信号转导模型。在2014年，Qi等人应用数学建模方法对干扰素-γ和IL-6的信号转导交互机制进行研究。在IL-6信号单独刺激下，在同一时间STAT1*最大浓度值是最大浓度值的三分之一，STAT3相比于STAT1有着更强的激活。[9]

一、材料与方法

本章将对数学模拟实验所利用的建模工具及统计方法所用工具进行介绍。

（一）建模工具COPASI及IL-6数学模型介绍

COPASI是用来构建和分析系统生物模型的工具。本文操作流程是打开软件，它运行时界面有两大模块左侧模块显示软件的各个功能层次，右侧模块显示的是各反应公式和参数的设定。双击Biochemical后紧接着双击species，根据研究需要分别或协同改变右侧gp130和gp80的初始浓度，之后双击tasks并通过Tasks模块下的Time course进行模型构建，最后单击run并且根据结果总结出分别或协同改变gp130和gp80的初始浓度对IL-6信号转导的影响。

（二）统计学方法

SPSS“统计产品与服务解决方案”软件，它的统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、生存分析等等。[10]本文中使用的是SPSS软件对实验数据进行皮尔逊相关性或多元线性回归分析，并计算其统计显著性水平。

二、结果与分析

本文以0.1nM的IL-6作为模型输入，在不同gp130和PP2的初始浓度下进行12小时的IL-6信号转导数学模拟（在数学模拟模型中PP2和gp130初始浓度分别是60nM和0.8nM，我们分别改变gp130和PP2的初始浓度为其0.25、0.5、1、2和4倍值）。此外，应用SPSS工具进行相关性分析和多元回归分析，阐释gp130和PP2初始浓度的变化对IL-6信号转导过程的影响。

（一）扰动PP2对IL-6信号转导影响

扰动PP2的初始浓度探究扰动PP2对IL-6信号转导影响。结果显示，STAT3*与PP2呈极显著负相关，STAT1*与PP2极显著负相关，PP2对IL-6信号转导信号有抑制作用呈负相关。

如图1A所示，在IL-6信号刺激下，STAT3*在0.6小时达到最大浓度368nM，随后浓度不断下降，最终在10小时后达到其稳定浓度47nM。STAT1*在0.6小时达到最大浓度109nM，并且在9小时后逐渐达到稳定浓度10nM。如图1B所示，STAT3*在0.6小时达到最大浓度350nM，在11小时后达到稳定浓度37nM。STAT1*在0.5小时达到最大浓度102nM，并快速降低，在8小时后达到稳定浓度9nM。如图1C所示，STAT3*在0.5小时达到最大浓度320nM，在11小时后达到稳定浓度30nM。STAT1*在0.5小时达到最大浓度94nM，并快速降低，在6小时后达到稳定浓度7nM。

如图1D所示，STAT3*在0.5小时达到最大浓度285nM，在8小时后达到稳定浓度32nM。STAT1*在0.5小时达到最大浓度82nM，并快速降低，在6.5小时后达到稳定浓度7nM。如图1E所示，STAT3*在0.5小时达到其最大浓度250nM，在8小时后达到其稳定浓度34nM。STAT1*在0.5小时达到最大浓度70nM并快速降低，在6.5小时后达到稳定浓度8nM。分别以STAT3*与STAT1*在不同浓度的PP2下所能达到的最大浓度值做柱形图，如图1F所示在磷酸酶PP2的初始浓度逐渐增大的情况下，STAT3*与STAT1*的最大浓度在不断地变小。STAT3*与PP2浓度极显著负相关（相关系数为-0.962，P值为0.009）。STAT1*与PP2浓度极显著负相关（相关系数为-0.967，P值为0.007）。本实验验证了已有的实验结果在IL-6的信号转导模拟分析中STAT3相比于STAT1有着更强的激活。由于IL-6对STAT3有偏好性，下文的研究中我們皆以STAT3*的浓度变化为代表来进行IL-6的信号响应研究。

图1不同PP2初始浓度下IL-6信号转导模式的变化

（A-E）中分别表示在不同PP2初始浓度下STAT*1和STAT*3的浓度时序性变化模式。F表示在不同PP2的浓度下STAT*1和STAT*3的最高浓度水平。

（二）协同扰动受体gp130与PP2对IL-6信号转导影响

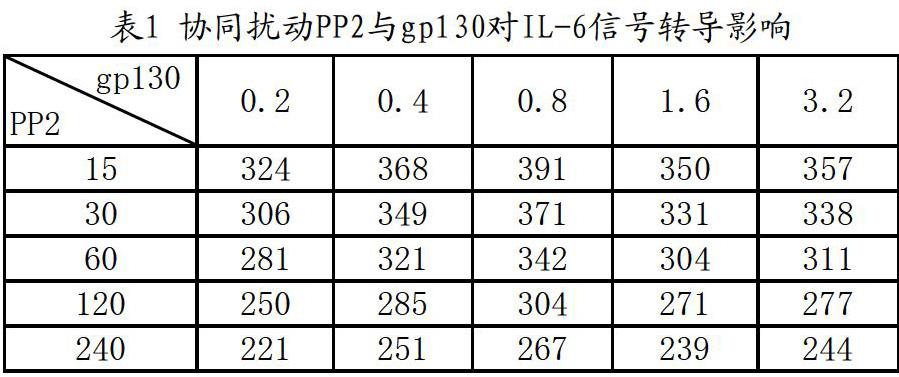
如表1所示，可知无论pp2如何调整，STAT3*的最大浓度都为整个表中最大数值。当pp2浓度升高STAT3*的最大浓度不断减小。根据SPSS软件的标准回归系数得出gp130浓度与IL-6信号转导之间不显著正相关。蛋白pp2浓度与IL-6的信号转导极显著负相关。对于IL-6的信号转导来说最适宜的受体gp130浓度为模型初始浓度，pp2与IL-6的信号转导呈极显著负相关。

三、结论

本文获得了一系列重要结论。首先，单独扰动pp2的初始浓度发现增加pp2的初始浓度能够显著抑制IL-6信号转导的强度，与STAT1*和STAT3*的最大浓度呈显著负相关。其次，单独扰动受体gp130的初始浓度发现受体gp130与IL-6的转导呈一定水平正相关。但不具有统计学显著性。最后，同时扰动受体gp130与pp2初始浓度的模拟结果显示，gp130与IL-6信号转导不顯著正相关，对于IL-6的信号转导来说，最适宜的受体浓度为模型初始浓度，无论在何种浓度的gp130下增加pp2的初始浓度能够显著抑制白介素-6信号转导的强度，多元回归分析同样证实了以上结果。这些结果的获得更进一步加深了我们对IL-6的信号转导模拟分析机制的了解，可能为治疗糖尿病、心肌肥大和男性肝癌等疾病提供理论支持。

【参考文献】

[1]蒋太交，薛艳红，徐涛.系统生物学——生命科学的新领域[J].生物化学与生物物理进展，2004，31（11）：957-964.

[2]王川.系统生物学——后基因组时代的生物学[J].生物学通报，2006，41（01）：19-21.

[3]常畅.系统生物学——系统生物学的研究进展[J].生物学通报，2007，42（06）：18-19.

[4]Levy DE，Darnell JE，Jr.Stats：transcriptional control and biological impact[J].Nature reviews Molecula cell biology，2002，3（09）：

651-662.

[5]Heinrich PC，Behrmann I，Haan S， etal. Principles of interleukin （IL）-6-type cytokine signalling and its regulation[J].The Biochemical journal，2003，374（Pt 1）：1-20.

[6]刘巍.白介素-6与心血管疾病[J].国际免疫学杂志，2006，29（01）：37-40.

[7]李清明，舒仁明，王家驷等.血清白介素-6在诊断肝细胞肝癌中的临床价值研究[J].川北医学院学报，2011，26（03）：251-253.

[8]李代挑，钟远伦，邱正强.肿瘤坏死因子白介素-6等细胞因子变化与左心功能不全的关系[J].河北医学，2014，20（02）：216-218.

[9]齐云峰.基于系统生物学方法的干扰素-γ和白介素-6信号转导通路建模以及抗癌药物诱导细胞凋亡机制的研究[D].博士论文，2014，5：35.

[10]翁心真.多元回归分析的软件求解和案例解读[J].数理统计与管理，2000，20（05）：23-26.

责任编辑：杨柳