基于单相dq变换与改进PRONY算法的牵引网低频振荡检测方法

2016-10-21中国电力科学研究院北京100192北京交通大学电气工程学院北京100044

西南交通大学学报 2016年5期

（1.中国电力科学研究院，北京100192；2.北京交通大学电气工程学院，北京100044）

牵引供电系统中的电气低频振荡现象会引发机车牵引变流器封锁，从而造成大面积发车延误.为解决这一问题，本文通过大量实测数据分析，给出了振荡时网压和网流的数学描述，并结合简单的车网电气模型简要阐明了网压低频振荡发生机制.根据牵引网单相供电的特点，提出使用网压信dq分解得到的d轴分量作为低频振荡的表征信号和检测对象，设计了以改进PRONY算法为基础的辨识低频振荡主导模式的检测方法.利用低频振荡案例中的实测数据对该检测方法进行验证，结果表明：本文设计的检测方法可以在1.4 s内对频率小于30 Hz、幅值大于0.01网压标幺值的低频振荡进行识别、计算出振荡主导模式并发出告警信号.

牵引网；低频振荡；单相dq变换；改进PRONY算法

电力系统发生的低频振荡现象［1］以往很少出现在单相供电的牵引网中.由于新型交直交传动动车组与电力机车（下文统一简称机车）陆续投入使用，最近几年我国电气化铁道牵引供电系统中多次出现牵引网电压低频振荡现象：在同一供电区段内空载整备的某种型号机车超过一定临界数目时，牵引网电压出现低频振荡，此时该型号机车会发生因牵引封锁而无法正常开出的状况.这种车网低频振荡多次造成列车发车延误，影响了铁路运输秩序.事实上这种现象不仅在我国单相50 Hz、25 kV供电制式牵引网中发生，国外的单相16.7 Hz、15 kV与单相25 Hz、11 kV供电制式牵引网都曾发生过类似的问题［2］.针对牵引供电系统发生的车网低频振荡现象，有必要对电压、电流的振荡模式进行分析，提出有效的检测方法，以便在车上或变电所中采取针对性的技术对策.

低频振荡的辨识方法有多种，例如FFT分析、小波分析等［3］.FFT算法辨识出的频率精度受数据窗的限制，例如，大秦线湖东机务段HXD1电力机车引发的低频振荡频率是3～4 Hz之间的非整数频率，如果振荡频率检测精度要达到0.01 Hz则需要100 s的数据窗，FFT算法无法实现实时快速检测.小波分析在低频部分有较高的频率分辨能力，不过小波分析的结果是一个频段而非明确的频率点，并且小波函数也很难统一构造.PRONY算法则用指数函数的线性组合来拟合实测数据，既可以获得准确的振荡频率，又不需要很长时间的数据窗，并且可以描述振荡信号是处于过阻尼状态、欠阻尼状态还是一个相对稳定的振荡状态，在电力系统低频振荡辨识中已得到广泛应用［4］.本文的目的是结合牵引网低频振荡的特点，对已有的PRONY算法进行针对性的改进，设计出适用的检测方法.

在第1节中，基于大量实测数据给出了牵引网低频振荡时网压、网流信号的统一数学描述，并简要阐述了牵引网低频振荡的发生机制.在第2节中，对网压信号使用单相dq变换技术［5-6］分解出d轴分量，提出将其作为低频振荡的表征信号.在第3节中，基于单相dq变换和改进PRONY算法设计出低频振荡的检测方法.在第4节中，以发生在青岛动车所和湖东机务段的两次低频振荡现象为例，利用现场测试数据验证了该方法的有效性.

1 牵引网低频振荡特征分析

1.1 电气模型

与电力系统低频振荡的负阻尼机理［1］不同，国内发生的牵引网低频振荡与发电机的励磁绕组和机械阻尼都没有直接关系，牵引网作为电力系统的一个终端配电网，在分析低频振荡时可以在馈线口处将牵引变电所及高压电力系统等值为理想无穷大电压源和阻抗相串联的戴维南等效电路［7-8］.使用最简化的集中阻抗参数模型描述牵引网，因为低频振荡现象不涉及高次谐波，牵引网分布电容影响可以忽略.

图1为含多台机车的牵引供电系统简化电气模型，图中：ug代表理想电压源；u为机车处牵引网电压（网压）；i是电源供出的总电流（总网流）；i1、i2是机车1和2分别取用的电流（网流）；L为高压电力系统的系统电感、牵引变电所变压器漏感和牵引网集中参数模型中的电感之和；R为3者的电阻之和（远小于电抗，通常在计算中可以忽略）.

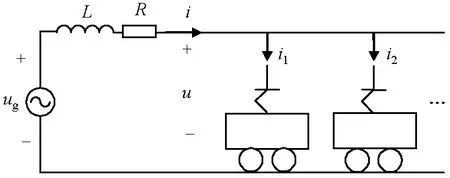
图1 低频振荡电气模型Fig.1 Electrical model used in low-frequency oscillation analysis

1.2 网压和网流的数学描述

振荡频率是车网低频振荡的重要参数，表1总结了国内近几年发生的低频振荡案例［7，9］，根据实测网压和网流数据，分别给出了振荡频率fl.

通过对大量低频振荡网压和网流实测数据的分析及拟合验证，得出发生低频振荡时网压的统一数学描述为

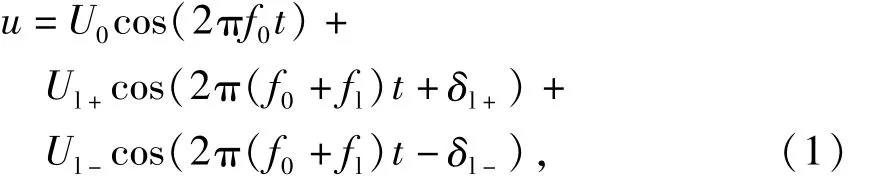
网流的统一数学描述为

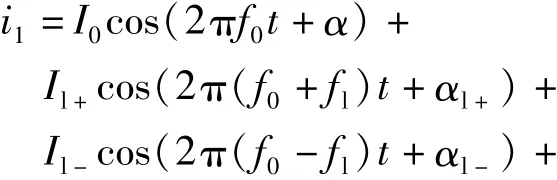
两式中均不包括由PWM控制引起的整数次谐波（不影响低频振荡分析，不在本文探讨范围之内）.进一步分析表明，式（1）、（2）中（f0+fl）分量和（f0-fl）分量的幅值大小一般不同，往往差别较大甚至其一为0，而式（2）中fl分量幅值一般很小或者为0.附录A列出了表1中序号1和3案例中的低频振荡网压、网流某时刻的数学表达式.

可以看出，网压和网流信号中基波频率附近的间谐波是使二者波形出现振荡的主要原因.若不考虑幅值较小的低频fl分量，振荡波形中基波频率左右两侧间谐波的频率关于基波频率对称，并且距离恰好都为fl，这可以理解为对基波幅值进行频率为fl的不对称调制.这也是把发生在牵引供电系统中的这种车网低频率共振现象称作低频振荡的原因.

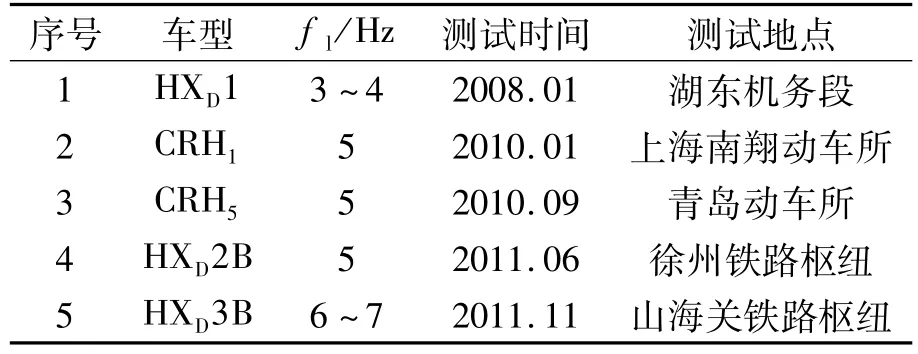
表1 牵引网低频振荡Tab.1 Low-frequency oscillations in traction power supply systems

1.3 网压低频振荡产生机制

初步研究表明，车网低频振荡现象一般发生在电源阻抗较大时，同一供电区段有多台同型号机车同时升弓带电（空载）的条件下，这时，由于交直交机车网侧整流器控制参数与电源阻抗的匹配不当，使得机车网流i1除工频外，还产生了如式（2）所示的（f0+fl）分量、（f0-fl）分量及fl分量.机车产生该间谐波分量的详细机理［8］不在本文的讨论范围内.

网流i1流经牵引网阻抗时，会形成牵引网压降.发生的低频振荡实际案例表明，同一区段的机车在发生低频振荡时，网流是同步的，并且在稳定振荡时不同机车吸取的电流瞬时值基本相等（见附录B）.振荡的网流会导致网压振荡，多台机车网流的叠加会导致网压的较大幅度振荡，反过来又进一步影响网流，最终呈现相对稳定的较大幅值的网压、网流振荡.

由图1可知，忽略电阻时，由多台机车网流造成的牵引网总压降为

式中：nl为机车数.

机车处网压可以通过理想电源电压与总压降的差表示

由式（2）、（3）可知，Δu应包含4个频率分量，但因为Il和fl相对于其他分量较小，所以Δu中可以忽略fl分量.这样u仅含3个频率分量，与式（1）中通过实测数据总结出的网压统一表达式相符.

2 牵引网低频振荡表征信号

选取呈现0.2～3.0 Hz波动的三相有功功率或功角曲线进行低频振荡模式分析.而对于作为独特配电网的牵引供电系统而言，不存在功角概念，并且由于单相供电，瞬时功率也存在显著的2倍工频振荡分量，无法直接找到一个能表征低频振荡特征的可测电气量.

单相dq轴控制技术已经广泛应用在单相整流器中［6-7］.主要思路是以网压为参考量（α轴），并虚拟出一个滞后参考量90°的分量（β轴），然后采用三相系统中的派克变换将两相静止坐标系下的α、β分量转换为同步旋转坐标系下的dq轴分量，这样d轴分量就代表网压的工频幅值，见图2，其中ω0= 2πf0，T=1/f0，e-sT/4表示延时1/4工频周期.

图2 单相dq变换Fig.2 Single-phase dq transformation

在发生低频振荡时，尽管网压含有非工频分量，但其幅值与工频分量幅值相比差一个数量级，所以网压信号的过零点与无振荡时很接近，故单相锁相环输出sin（ω0t）和cos（ω0t）可以视为幅值为1、频率为f0的参考正、余弦波.

由式（1）和图2可以计算出，发生低频振荡时网压经过单相dq变换后，其d轴分量的近似表达式为

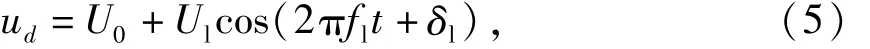
式中：ud为工频幅值U0的直流分量与频率为fl的低频交流分量之和；Ul和δl分别为两个非工频分量幅值和相位的合成，

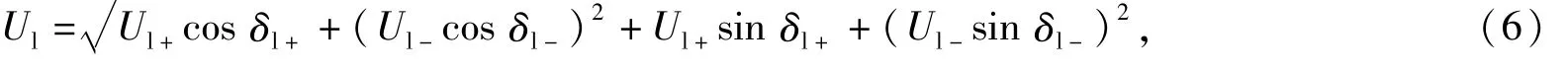
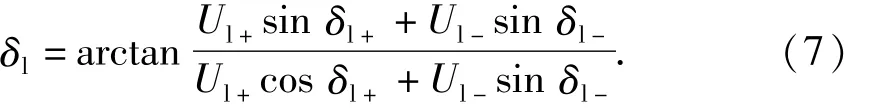
从式（6）和（7）中可以看出，该交流分量的幅值和相位包含了网压u中的全部非工频分量的信息，其幅值表示低频振荡发生的剧烈程度，频率即为前文中定义的低频振荡频率fl，故ud可以作为牵引网低频振荡的表征信号用于检测.

3 牵引网低频振荡检测方法

3.1 PRONY算法原理

在PRONY算法中，信号ud的样点序列ud［n］由多个具有不同幅值、相位、衰减因子、频率的指数函数的线性组合［n］来近似描述，

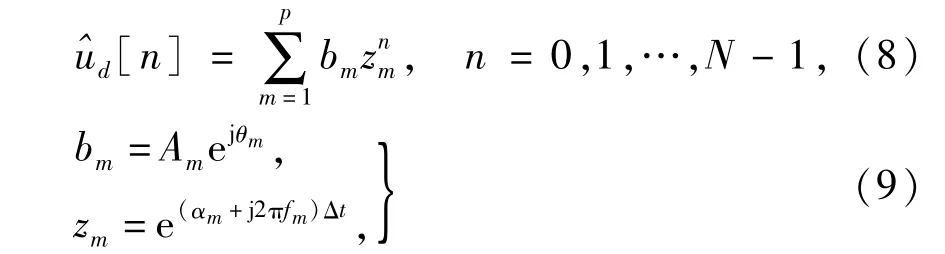
式中：Am为幅值；θm为相位；αm为衰减因子；fm为频率；Δt为采样间隔；N为数据窗长；p为模型阶数.

经过推导［10］，序列ud［n］与估［n］的误差可表示为自回归-滑动平均模型（ARMA（p，p）），并具有相同的AR参数和MA参数.PRONY算法采用最小二乘法进行参数估计，首先构造二阶样本矩R，其元素r表示为

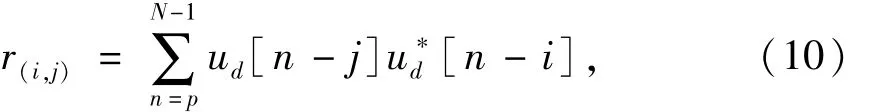
然后解线性方程组：

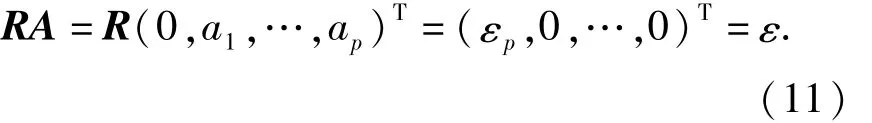
解得向量A，其中a1，…，ap为ARMA（p，p）模型中的AR参数，则A定义为AR参数向量.通过解以a1，…，ap为常系数的线性齐次差分方程的根得到zm［10］，对照式（9）可得到αm和fm.再由

3.2 检测流程

PRONY算法在辨识实际含噪声信号时会受噪声影响导致计算量增大和精度降低［11］，而PRONY模型中阶数p的选择也会对辨识准确性产生影响［11］.文献［12］提出的通过数据预处理与定阶算法改进PRONY算法很好地控制了计算量与计算精度，故本文基于改进PRONY算法设计检测流程.

PRONY算法一般在采样频率固定的情况下，数据窗长度越大其参数预测的精度就越高.一般至少要包括2个以上完整的波动周期［12］，我国目前出现的牵引网低频振荡的频率在3.0～7.5 Hz之间，经过对大量实测数据的试验，使用1 s的时间窗可以较为准确地检测出振荡频率.

由第2节的分析可知，表征信号ud来自牵引网的网压信号u，该信号可以取自机车上的网压传感器，也可以取自牵引变电所的母线电压互感器.信号经过有限冲击响应数字滤波器（FIRDF）后通过单相软件锁相环［13］（SPLL）进行dq变换得到网压d轴信号ud；然后根据选择的数据窗长建立二阶样本矩R；对R用奇异值分解（SVD）算法定阶后采用总体二乘法（TLS）计算PRONY模型中的自回归（AR）参数，并进一步求解出PRONY模型中的剩余全部参数；最后根据低频振荡的合理频率与幅值范围筛选出低频振荡主导模式并同时输出振荡频率与判断信号.整体检测程序流程如图3所示.

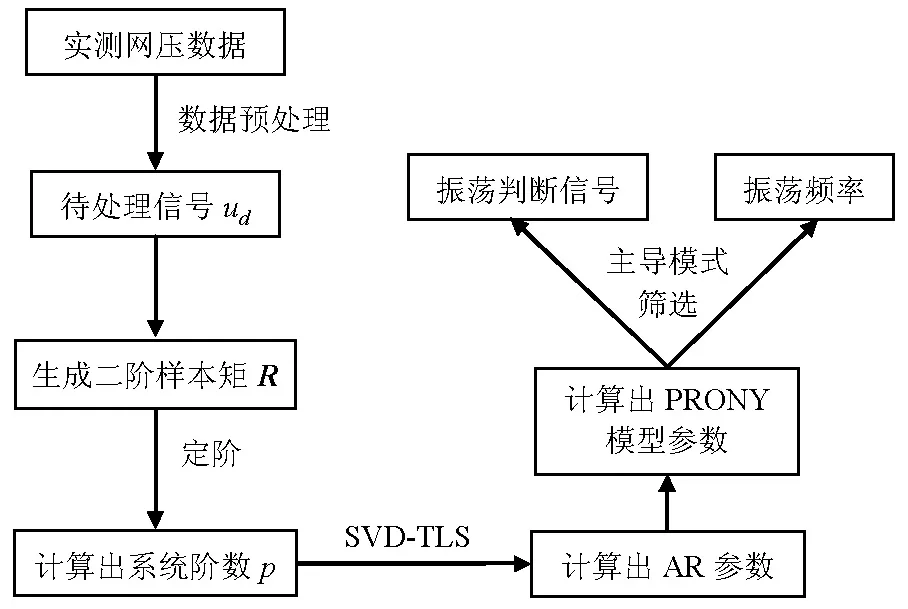
图3 低频振荡检测流程图Fig.3 Low-frequency oscillation detection flowchart

（1）数据预处理

因为网压信号u中包含工频频率非整数倍的分量，所以为了数字滤波后的信号中工频相位不变，并且其他频率分量能保持可以预计的相位关系，本文采用异步采样并使用第一类线性相位关系［14］滤波器.设滤波前的原始信号的采样序列为u［n］，则滤波后的序列uα［n］满足［15］：

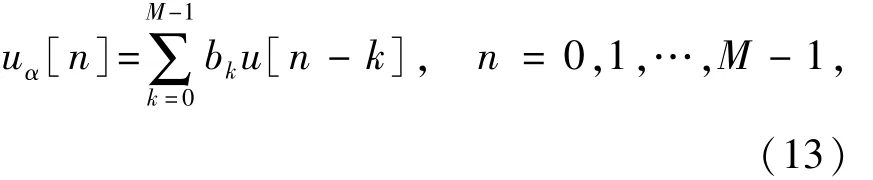
式中：M为滤波器阶数；bk为第（n-k）个原始信号对应的滤波器系数.滤波后不同频率分量的相移关系满足［14］：

式中：fs为采样频率.

经多次试验发现低于10 kHz的采样频率将会导致表征信号ud的抽样序列有较大的失真，进而导致PRONY算法无法正确辨识出振荡模式，故本文取fs=10 kHz.本文使用布莱克曼窗设计滤波器系数，为使工频无相移并且保证网压信号的各频率分量滤波后的幅值基本无变化，阶数M取401，系数bk使用Matlab中的fdatool数字滤波器设计工具箱计算，并设置FIR DF实现结构为直接Ⅰ型［14］.

为了实现单相dq变换，uα［n］作为α轴分量，由于（M-1）为两个工频周期的采样点总数，滞后α轴分量1/4工频周期的β轴分量uβ［n］为

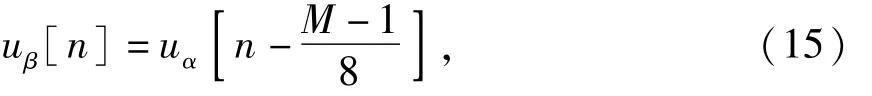
由式（15）可以看出，β轴分量可由α轴分量进行序列延迟后得到.通过SPLL输出相位序列θ［n］，查表得到参考正余弦信号，再通过派克变换得到dq轴信号，如图4所示.

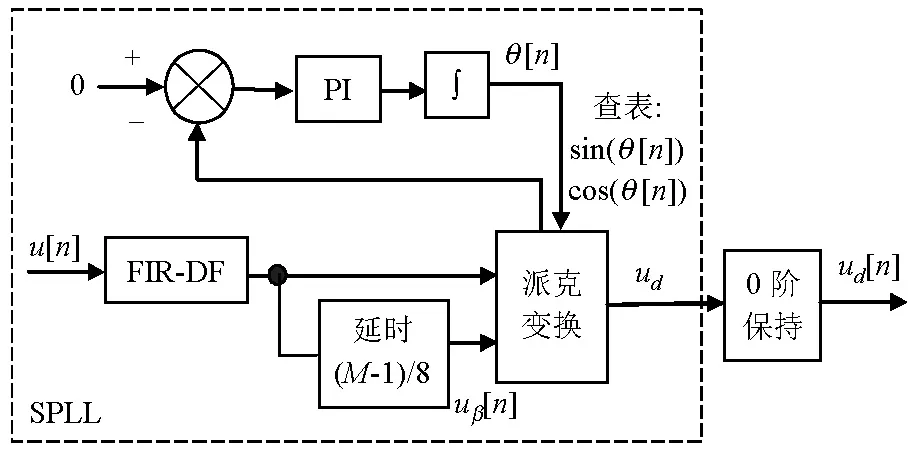
图4 数据预处理流程图Fig.4 Data preprocessing flowchart

在SPLL中，PI调节器（比例系数51，积分系数64.56）与积分器是先运用双线性变换把二者在s域的传递函数变换到z域，再将z域传递函数表示的差分方程转为输入输出数字信号的关系表达式［13］，本文因为篇幅关系对此不再详述.值得注意的是，当电网频率波动时（假设波动范围为49～ 51 Hz），由于滤波器和延时环节参数都是在标准频率50 Hz下设置的定值，所以派克变换得出的ud会出现误差.经仿真发现，当电网频率为49 Hz时，ud中的fl分量出现最大幅值误差1.1%，这不会对检测产生明显影响.但此时ud中会含有幅值达到fl分量29.7%、频率为98 Hz的间谐波分量，需要在后续频率筛选环节中去掉.

由式（5）可知，ud的有效交流分量是频率fl的低频分量，辨识其准确频率无需采样频率为10 kHz的序列.根据香农采样定理，采样频率要大于信号最高频率的2倍，本文在留有一定频率裕度的情况下选用100 Hz的采样频率，即采用0.01 s的0阶保持器降低原输出序列频率，得到待检测的离散序列ud［n］.

（2）生成二阶样本矩R

先对数据去直流（减去平均值）处理，为尽量保留全部信息，模型阶数p先取最大值pe=N/2（采用1 s数据窗长时N=100）.故R的阶数为（pe+1），其元素已在式（10）中定义.

（3）定阶

尽管经过滤波处理，信号ud中仍然带有噪声，导致PRONY算法会计算出个数多于p的振荡模式，所以需要定阶算法计算阶数p，以保证计算结果中只含有实际振荡模式.

本文采用基于奇异值分解（SVD）的归一化比值法来确定阶数p.确定有效阶数p实质上是确定R的有效秩［16］.故对矩阵R进行SVD，得到

式中：U为pe阶酉矩阵；V为（pe+1）阶酉矩阵；VH为V的转置共轭矩阵；Σ为（pe+1）阶矩阵，其类对角线上元素Σ（i，i）为从大到小排列的矩阵R的奇异值σi，而其余元素全为0.

由于噪声空间的存在，R的秩大于p，甚至为满秩pe，所以需要形成一个新矩阵来近似代替R：

式中：Σp为Σ前p个奇异值不变其余均置0的近似.显然p取值越大，Rp越逼近R.定义为

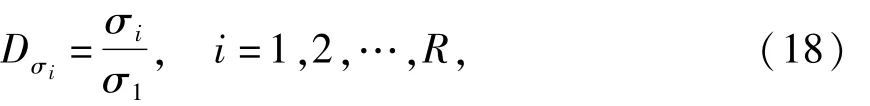
式中：R为R的秩.i由1向R逐渐靠近的过程中，Dσi渐渐减小，由于奇异值反应了各个分量在动态过程中所起的作用大小［16］，所以很自然地舍弃起作用小的分量（噪声）.即设定一个阈值Dt，经试验本文取0.001，当Dσp＜Dt时得到模型阶数p.

（4）计算AR参数

本文采用奇异值分解总体二乘法SVD-TLS方法求解AR参数向量A，可解得［17］

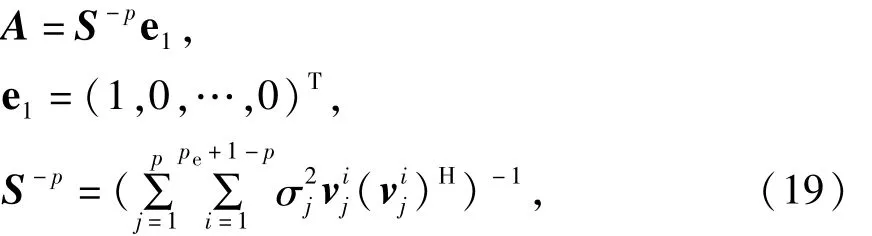
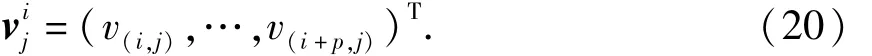
（5）计算PRONY模型参数

已知AR参数后，PRONY模型参数Am、θm、αm和fm可由3.1节介绍的方法求出.

（6）主导模式筛选

由式（5）可知，对于牵引网的低频振荡，主导模式数往往等于1，即只有一种型号的机车引发低频振荡（不过不排除今后出现多种机车引发低频振荡的现象发生）.然而通过实际计算可知，经过上述5个步骤计算出PRONY模型还是有些幅值很小或者衰减很快的非主导模式分量需要被筛减，根据大量实测数据试验，并考虑电网频率波动产生的影响，本文设定筛选的频率范围为1～30 Hz，幅值大于0.01（基准幅值为35 355 V的标幺值）可以有效地筛选出牵引网低频振荡主导振荡模式.

根据筛选后的结果，检测程序设置如果未筛选到符合条件的主导振荡模式，则检测程序输出振荡判断信号0，反之则输出1，并将振荡频率同时输出.

4 实例验证

4.1 青岛动车所低频振荡（例1）分析结果

在CRH5型动车组上测得的1 s长的网压数据经过数据预处理后，得到uα与ud如图5所示，可以看出ud曲线为uα曲线的包络线，可以很好地表示网压低频振荡的特征.

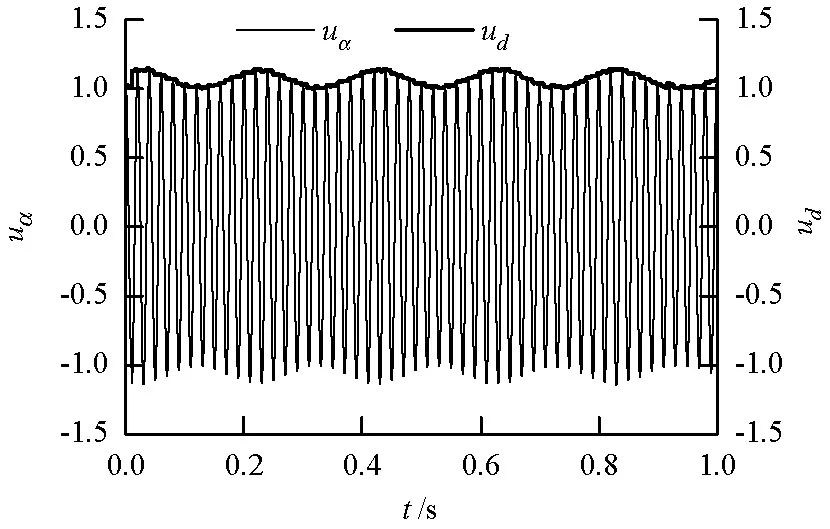
图5 例1 uα和ud（标幺值）Fig.5 uα（p.u.）and ud（p.u.）in case 1

对实际的ud曲线与使用改进PRONY算法拟合的曲线对比如图6所示，二者的接近程度用相关系数γ为

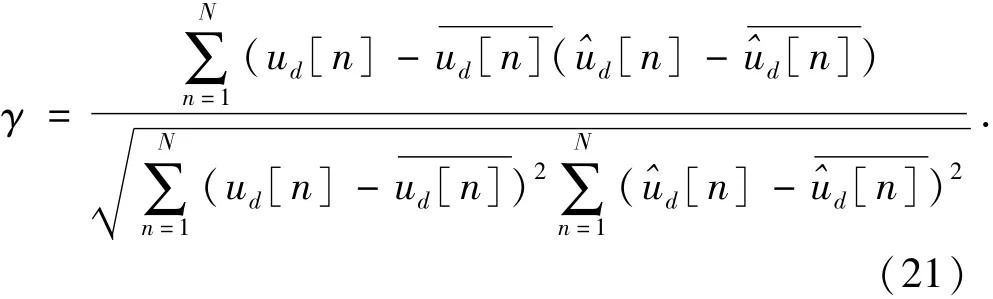
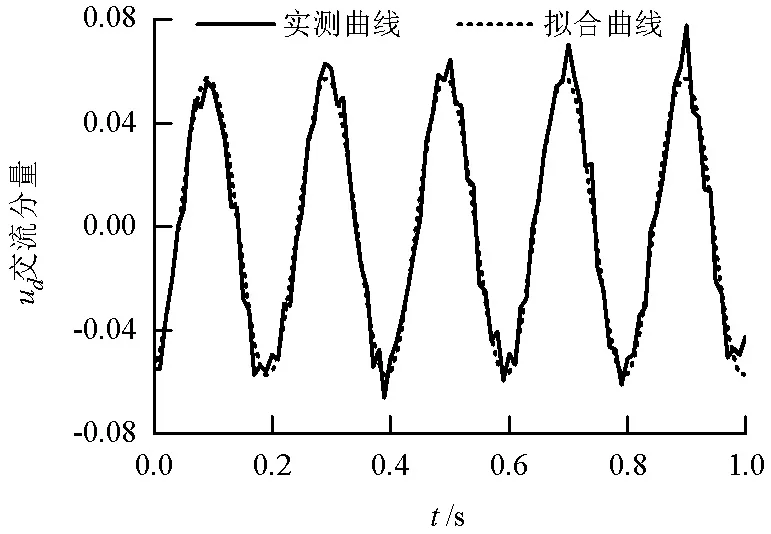
图6 例1 ud交流分量（标幺值）Fig.6 AC component of ud（p.u.）in case 1

计算时取1 s的时间窗长（N=100）算得相关系数γ=98.67%，说明了本文算法的拟合精度达到要求.辨识出的振荡模式结果见表2.

表2 例1主导振荡模式Tab.2 Dominant oscillation pattern in case 1

4.2 湖东机务段振荡（例2）分析结果

在HXD1型电力机车上测得的1 s长的网压数据经过数据预处理后，得到uα与ud如图7所示.从图7中可以看出，例2中ud也很好地表征了低频振荡.

用改进PRONY算法拟合的ud曲线和实际曲线相关系数γ=99.82%，二者对比见图8.辨识出的振荡模式结果见表3.

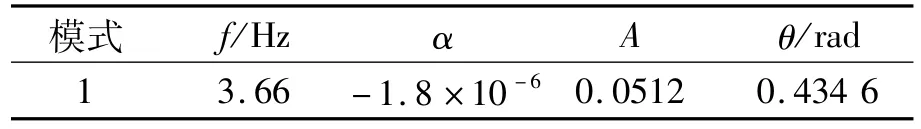
表3 例2主导振荡模式Tab.3 Dominant oscillation pattern in case 2

4.3 检测程序运行结果

本文根据第3节介绍的检测方法在Matlab平台上用m语言编写了检测程序，并使用了一段取自车上网压传感器的实测数据验证检测程序的实时运行效果.试验数据来自例1，取10 s网压出现振荡后平稳，又再次振荡的过程，程序运行结果见图9.

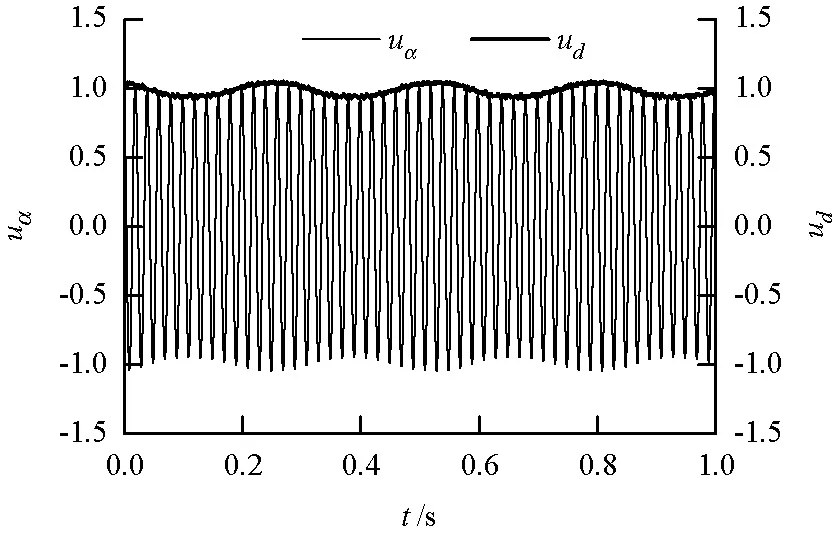
图7 例2 uα和ud（标幺值）Fig.7 uα（p.u.）and ud（p.u.）in case 2

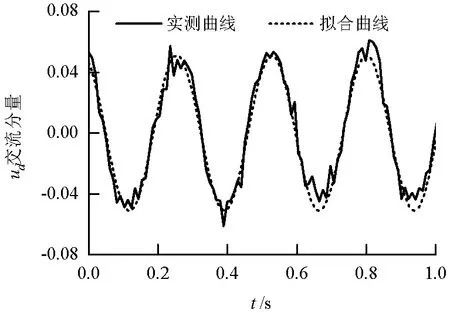
图8 例2 ud交流分量（标幺值）Fig.8 AC component of ud（p.u.）in case 2

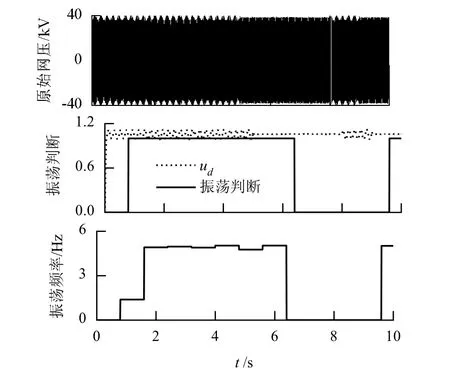
图9 检测程序实时运行结果Fig.9 Real-time simulation result of detection procedure

因为单相dq变换一开始需要很小的一段缓冲数据来构造uβ的缘故，图9中的ud曲线在0.1 s左右的冲击值后到达正常.从图9中可以看出由于数据窗为1 s的长度，再加上数据传输过程中设置的数据重叠等因素，振荡判断信号相比实际振荡有1.4 s的滞后.而振荡频率信号也由于开始需要缓冲数据来构造uβ，所以第一次频率输出不准，1.4 s后恢复到5 Hz左右的实际振荡频率.

5 结论

（1）牵引网低频振荡发生时，网流的数学表达式除了含有工频f0分量，还含有非工频的（f0+fl）分量和（f0-fl）分量，二者幅值不等，同时还可能含有一个低频fl分量.振荡的网流流经牵引网时产生压降，故振荡的网压中所含有的非工频分量是由网流和牵引网阻抗决定的.低频振荡发生时，网压波形表现为一个低频信号对正常工频波形进行不对称调制.

（2）网压信号经过单相dq变换后的d轴分量ud为网压瞬时值的包络线，当发生低频振荡时，ud中产生的交流分量完全由振荡网压中的非工频分量决定，可以作为低频振荡的表征信号.

（3）改进PRONY算法可用于ud交流分量的检测，其结果可以准确地表示牵引网低频振荡的主导振荡模式.

（4）按本文方法设计的检测程序可以有效地检测出网压低频振荡的发生和停止.该程序可以安装在机车上或变电所中，对网压实时监测，以便在检测到低频振荡时，对机车的调度运行提供信息支持.

［1］王铁强，贺仁睦，王卫国，等.电力系统低频振荡机理的研究［J］.中国电机工程学报，2002，22（2）：21-25.

WANG Tieqiang，HE Renmu，WANG Weiguo，et al.The mechanism study of low frequency oscillation in power system［J］.Journal of CSEE，2002，22（2）：21-25.

［2］ DANIELSEN S，MOLINAS M，TOFTEVAAG T，et al. Constant power load characteristic's influence on the low-frequency interaction between advanced electrical rail vehicle and railway traction power supply with rotary converters［C］∥ Proc. Modern Electric Traction. Gdansk：［s.n.］，2009：1-6.

［3］ HOJO M，OHNISHI T，MITANI Y，et al.Observation of frequency oscillation in western Japan 60 Hz power system based on multiple synchronized phasor measurements［C］∥Power Tech Conference.Bologna：IEEE Press，2003：2-6.

［4］肖晋宇，谢小荣，胡志祥，等.电力系统低频振荡在线辨识的改进Prony算法［J］.清华大学学报：自然科学版，2004，44（7）：883-887.

XIAO Jinyu，XIE Xiaorong，HU Zhixiang，et al. Improved Prony method for online identification of lowfrequency oscillations in power systems［J］.Journal of Tsinghua University：Science and Technology，2004，44（7）：883-887.

［5］ SALAETJ，ALEPUZ S，GILABERT A，etal. Comparison between two methods of DQ transformation for single phase converters control.Application to a 3-level boost rectifier［C］∥ Proc.Power Electronics Specialists Conference.Aachen：IEEE Press，2004：214-220.

［6］ MIRANDA U A，AREDESM，ROLIM L G B.A DQ synchronous reference frame current control for singlephase converters［C］∥ Proc. Power Electronics Specialists Conference.Recife：IEEE Press，2005：1377-1381.

［7］王晖，吴命利.动车组引起牵引供电系统网压低频振荡现象测试及分析［C］∥中国高等学校电力系统及其自动化专业第二十七届学术年会.秦皇岛：［s.n.］，2011：5-12.

［8］ WANG Hui，WU Mingli，et al.Analysis of lowfrequency oscillation in electric railways based on smallsignal modeling of vehicle-grid system in dq frame［J］. IEEE Transactions on Power Electronics，2015，30（9）：5318-5330.

［9］郑琼林.交流传动HXD1电力机车谐振原因分析与对策［J］.变频器世界，2009（5）：40-44.

ZHENG Qionglin.A probe on cause and solutions of the HXD1 AC locomotive's resonance［J］.The World of Inverters，2009（5）：40-44.

［10］王铁强.电力系统低频振荡共振机理的研究［D］.北京：华北电力大学，2001.

［11］胡昊明，郑伟，徐伟，等.Prony和HHT算法在低频振荡在线辨识中的适用性比较［J］.电力系统保护与控制，2013，41（14）：33-40.

HUHaoming，ZHENG Wei，XU Wei，etal. Comparison of the applicability of Prony and HHT algorithms for on-line identification of low-frequency oscillation［J］.Power System Protection and Control，2013，41（14）：33-40.

［12］刘森.基于PRONY算法的电力系统低频振荡在线辨识研究［D］.北京：华北电力大学，2006.

［13］张建斌.锁相与频率合成［M］.北京：科学出版社，2011：244-248.

［14］程佩青.数字信号处理教程［M］.北京：清华大学出版社，2001：466-508.

［15］任碧莹，钟彦儒，孙向东，等.基于有限冲击响应滤波器线性相移控制的单相系统数字锁相环［J］.电工技术学报，2008，23（8）：121-125.

REN Biying，ZHONG Yanru，SUN Xiangdong，et al. A digital phase-locked loop based on the linear phaseshifted controlimplemented by a finite impluse response filter for a single-phase power system［J］. Transactions of China Electrotechnical Society，2008，23（8）：121-125.

［16］熊俊杰，邢卫荣，万秋兰.Prony算法的低频振荡主导模式识别［J］.东南大学学报：自然科学版，2008，38（1）：64-68.

XIONG Junjie， XING Weirong， WAN Qiulan. Identification ofcontrolmodes in low frequency oscillation analysis by Prony method［J］.Journal of Southeast University：Natural Science Edition，2008，38（1）：64-68.

［17］朱学锋，吴晓琳.基于SVD-TLS的ARMA谱估计及应用［J］.战术导弹技术，2004（4）：29-33.

ZHU Xuefeng，WU Xiaolin.Spectral analysis using ARMA models based on SVD-TLS algorithm［J］. Tactical Missile Technology，2004（4）：29-33.

附录A

表A1 网压、网流数学描述Tab.A1 Mathematic description of line voltage and current

附录B

基于单相dq变换与改进PRONY算法的牵引网低频振荡检测方法

王晖1，2，吴命利2，李文锋1，王官宏1，李莹1，陶向宇1

Detection Method of Low-Frequency Oscillation in Traction Power Supply System Based on Single-Phase dq Transformation and Improved PRONY Algorithm

WANG Hui1，2， WU Mingli2， LI Wenfeng1， WANG Guanhong1， LI Ying1， TAO Xiangyu1
（1.China Electric Power Research Institute，Beijing 100192，China；2.School of Electrical Engineering，Beijing Jiaotong University，Beijing 100044，China）

Electrical low-frequency oscillation in traction power supply systems causes vehicle traction system shutdown，which results in severe service delay.The mathematical descriptions of the oscillated voltage and current were presented based on the analysis of a large amount of measured data.The line voltage oscillation mechanism was also explained in a brief way through a simple electrical model representing the traction power supply system and locomotives.Considering the features of the singlephase power supply，the d-axis component of the line voltage was obtained by a single-phase dq transformation，and chosen as the characteristic signal and the detection object.Then，a detection method was designed based on the improved PRONY algorithm to identify the dominant pattern of lowfrequency oscillation.The detection method was verified by the measured data from actual lowfrequency oscillation cases.The results show that the designed detection method can identify the lowfrequency oscillation with the frequency lower than 30Hz，magnitude over 0.01（p.u.），and calculate the dominant oscillation pattern and send out an alarm signal.

book=879,ebook=68

traction power supply system；low-frequency oscillation；single-phase dq transformation；improved PRONY algorithm

0258-2724（2016）05-0878-08

10.3969/j.issn.0258-2724.2016.05.009

TM935

2014-11-04

铁路总公司科研计划重点课题资助项目（2015J008-F）

王晖（1985—），男，博士，研究方向为牵引网低频振荡机理及抑制、电力电子化电网超、次同步振荡机理及抑制，E-mail：09117353@bjtu.edu.cn

吴命利（1971—），男，教授，博士生导师，研究方向为电气化铁道供电及城市轨道交通供电，电磁暂态计算与电力系统数字仿真，电能质量测试、评估与治理，E-mail：mlwu@bjtu.edu.cn

王晖，吴命利，李文锋，等.基于单相dq变换与改进PRONY算法的牵引网低频振荡检测方法［J］.西南交通大学学报，2016，51（5）：878-885.