求解拆卸线平衡问题的改进人工蜂群算法

（西南交通大学机械工程学院，四川成都610031）

（西南交通大学机械工程学院，四川成都610031）

大规模拆卸线平衡问题（disassembly line balancing problem，DLBP）是NP完全问题.为克服传统算法求解DLBP搜索过于随机、易于早熟，且求解难度随任务规模的增加呈指数级增长等不足，构建了基于最小化工作站、均衡负荷、尽早拆卸有危害和高需求零部件的DLBP多目标优化模型，在此基础上，提出了改进人工蜂群算法.该算法包括以下4个阶段：在初始解生成阶段，引入危害指标和需求指标，提升算法收敛性能；在雇佣蜂搜索阶段，采取可变步长搜索策略，增加对较优解的搜索深度，加速淘汰劣解；在观察蜂搜索阶段，采用常规搜索与蠕动搜索相结合的混合搜索策略；在侦察蜂搜索阶段，构造了基于分布估计的搜索策略，引导搜索过程.应用本文算法对70个测试问题进行求解，其中65个求得了最优解，寻优率为92.86%；对10个任务实例求得最优解的需求指标为9 730个，比蚁群算法减少了360个；52个任务实例的开启工作站数目、平滑率和拆卸成本3项指标均取得了更优的结果，求解较大规模问题的性能显著提升.

拆卸线平衡；人工蜂群算法；优化；拆卸

随着现代化进程的发展，物质资源极大丰富化，但同时也面临着大量寿命终了的机械、汽车、电器等产品等待回收处理问题.另一方面，当前资源、能源短缺问题日趋严重，传统的高投入、高产出模式难以持续，社会环境与资源问题日益突显，加之公民环保意识的不断增强，所有这些都在推动寻求废旧机电产品的新出路.

废旧机电产品的回收资源化处理是构建静脉产业的必由之路，在产品的回收过程中，产品拆卸过程是重要的环节，无论是对于具有众多零部件的大型产品还是对于回收数量很多的小型产品，实现拆卸过程的流水作业，在极大提高产品回收效率的同时，能有效降低拆卸成本，因此，受到了越来越多企业的重视.为解决流水化拆卸过程中拆卸任务分配不均衡等问题，学术界对拆卸线平衡问题展开了深入的研究.

文献［1］比较了拆卸线平衡问题（disassembly line balancing problem，DLBP）与装配线平衡问题［2］的异同点，并对影响拆卸线平衡的众多复杂因素进行了详细分析.文献［3］建立了破坏性拆卸影响下的单目标DLBP模型，并用分支定界法来求解该模型.其求解方法局限在数学规划层面，然而文献［4］证明了拆卸线平衡问题是一个NP（nondeterministic polynomial）完全问题，问题的求解难度会随着任务规模的增加呈几何级增长，传统的数学规划方法不适用于对大规模问题的求解.文献［5］提出了一种基于Pareto的蚁群算法求解多目标DLBP问题，其在建模阶段引入对拆卸成本的考量，使得研究的问题更加贴近生产实际，但其算法求解质量还有提升空间.文献［6］建立了关于拆卸费用的DLBP模型，并用启发式算法求解该模型.文献［7］考虑了最小化工作站数、平衡指数、危害指数、需求指数、最小化拆卸方向改变5个目标函数.文献［8］提出一种改进的蚁群算法，采用混合搜索策略，提高了算法在多目标优化方面的能力.文献［9］采用一种基于网络的最短路模型法求解并行DLBP问题，但该方法难以求解大规模问题.文献［10］引入变邻域搜索算法求解序列相关的拆卸线平衡问题，拓展了解决DLBP问题的新途径.文献［11］考虑了不确定拆卸时间的特殊情况，其所提算法对于多目标的优化能力不强，求解过程一味追求平衡而增加了大量的时间消耗.

本文针对传统算法在求解DLBP问题时的搜索过于随机、易陷入局部最优等不足，提出了一种改进的人工蜂群算法（artificialbeecolony algorithm，ABC）.ABC算法是一种模拟自然界中蜜蜂觅食行为而发展起来的群集智能优化算法［12］，与粒子群算法［13-14］等均属于群智能优化算法，具有结构简单、稳定性好等优点，在诸多优化问题中得到了广泛应用［15］，并表现出良好性能.本文根据ABC算法原理并结合DLBP问题的特点，构造了由一般产品通用的优化目标组成的多目标DLBP模型，并从初始解生成、雇佣蜂和观察蜂的邻域搜索策略、侦察蜂搜索策略等方面对算法进行了改进，进而通过对不同规模算例的测试来验证所提算法的求解性能.

1 多目标拆卸线平衡问题的数学模型

1.1 模型描述

假定待拆卸产品的每个零件对应一个拆卸任务，n为零件数目，T代表拆卸任务集合，则有

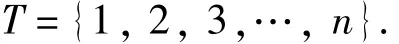
m为开启的工作站的数目，工作节拍用C表示，ti表示第i个工作站上分配的所有拆卸任务作业时间之和.用φij表示任务与工作站的关系，若任务j被分配到工作站i，则φij=1，否则φij=0.本文从4个方面构建DLBP问题的数学模型：最小化工作站数、均衡各工作站作业负荷、尽早拆除有危害零部件、尽早拆除高需求零部件.作业任务之间的优先关系用P表示，若任务p为任务q的前序任务，则P（p，q）=1，否则P（p，q）=0.

（1）最小化工作站数.工作站的开启意味着人力、物力等成本的投入，最小化工作站数能够将企业的投入成本降到最低，目标为

（2）均衡各工作站的作业负荷.为保证拆卸线高效运行，尽量降低产品在线阻塞，需要使各工作站的员工具有相对均衡的作业负荷，目标表示为

（3）尽早拆除危害性零部件.回收产品中经常包含有毒有害物质，例如重金属、含铅玻璃、氯氟烃等.这些物质不但会对作业员的人身安全以及自然环境安全造成严重威胁，而且由于其需要特殊的工具或手段进行处理，还会对整个拆卸线的工作效率造成影响.对于这类危害性零部件，应尽早拆除.目标表示为

式中：Sk表示拆卸序列的第k个位置的零件编号.

（4）尽早拆卸高需求的零件.对于高需求的零部件，为了尽早满足供给同时避免其在线上的损伤，应尽早予以拆除.目标表示为

式中：dSk表示编号为Sk的零件的需求量.

1.2 数学模型

基于以上考虑，构建的多目标DLBP数学模型如下.

目标函数：min｛f1，f2，f3，f4｝，

约束条件：

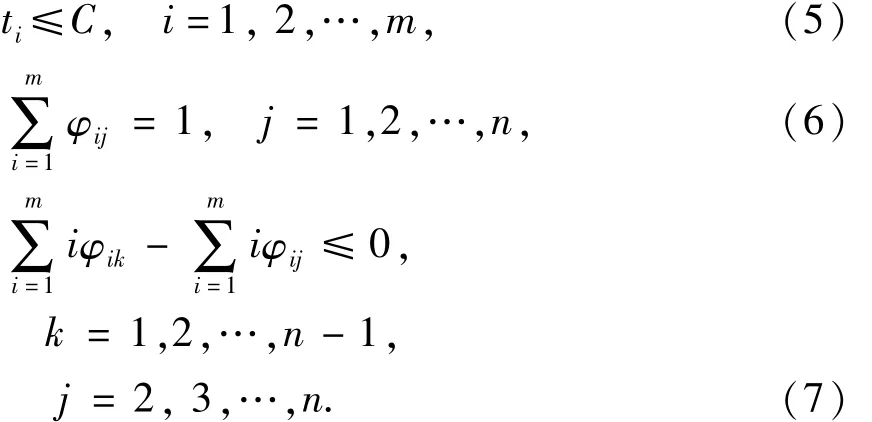
式（5）为节拍时间约束，即被分配到同一工作站的所有任务作业时间之和不能超过所设定的节拍时间.式（6）表示一项作业任务必须分配到某个工作站内完成，但不能同时分配到两个以上的工作站.式（7）表示任务之间的优先关系约束，即每个作业任务都应符合给定的优先顺序，如果作业k需在作业j前完成，则k就不能分配至j所在工作站的后续工作站中.

2 人工蜂群算法

人工蜂群智能优化算法是仿效蜜蜂采蜜过程而提出的一种仿生搜索算法［12］，利用了雇佣蜂、观察蜂和侦察蜂3个蜂种之间相互协作而体现出的群体智能行为.在运用ABC算法求解问题的过程中，将问题的可行解看做蜜源，将解的收益度作为考量花蜜丰富程度的指标.

DLBP的标准人工蜂群算法步骤如下［11］：

步骤1 初始化阶段.设定算法参数，如蜂群规模、雇佣蜂步长、循环次数及角色转变阈值Zuplimit.同时侦察蜂在全局范围内随机搜索初始解，开始时，令所有蜜蜂执行搜索任务，选择较好的初始解作为雇佣蜂采蜜的蜜源.

采用构造可选任务集和可分配任务集的方法构造可行解.首先，在当前位置i处，所有紧前任务都已分配的任务称为可选任务，组成可选任务集TEi；其次，从TEi中将作业时间超过工作站剩余时间的任务剔除，形成可分配任务集Trang，然后从Trang中随机选择任务分配.

步骤2 雇佣蜂阶段.雇佣蜂在现有解附近搜索，如果找到更好的解，就放弃现有解保留新解，依次对比f1～f4来确定食物源的优劣.常用的邻域搜索方法有交换法和插入法等.

步骤3 观察蜂阶段.求出雇佣蜂带回食物源的收益度，用解的收益度计算观察蜂跟随雇佣蜂的概率，

式中：Neb为雇佣蜂的数量；

Fi为第i只雇佣蜂所搜寻到的食物源的收益度.

观察蜂采用轮盘赌的方式选择跟随目标，食物源的收益度越好，被选择的可能性就越大.一只观察蜂在其跟随的雇佣蜂附近搜索到新解后，如果新解优于当前解，雇佣蜂就放弃现有解，获得新解.

步骤4 侦察蜂阶段.如果某一雇佣蜂代表的解经过Zuplimit次循环都没有得到优化，那么该雇佣蜂的角色转变为侦察蜂，并在全局范围内随机搜索新解.

步骤5 记录当前最优解.

步骤6 终止条件判定（是否达到设定的最大迭代次数），满足则退出，否则回到步骤2.

3 算法的分析与改进

ABC算法中，雇佣蜂和跟随的观察蜂在现有解的附近搜索，不断用附近更优的解替代现有解作为下一步的搜索中心.侦察蜂依靠在全局的随机搜索，为它们提供新的搜索中心.在贪婪选择的驱使下，雇佣蜂代表的解会逐渐向局部最优收敛，在参数Zuplimit的控制下侦察蜂获得在全局搜索的机会.局部搜索的深度和全局搜索的广度决定了算法的性能.标准的人工蜂群算法收敛速度快，但是搜索过于随机，易早熟，不利于多目标的搜索.因此本文对初始解生成策略、雇佣蜂步长和侦察蜂搜索策略进行改进，以克服标准算法的不足.

3.1 初始解生成策略的改进

文献［11］的初始解生成策略只考虑了节拍时间和优先关系的约束，并未加入危害性和需求因素.而基于优先顺序的多目标优化策略对后续目标的优化能力不足，因此，本文在生成初始解时加入危害性和需求因素，提高初始解针对这两个目标的质量.在从可分配任务集Trang中选择分配任务时，增大选择有危害和高需求任务的概率.基于此，设定Trang中每个任务被选择的概率为

式中：NC为可分配任务集Trang中任务数；

PHi、PDi分别为零件i的危害指数和需求指数占Trang中所有任务该项指数之和的比重.

3.2 步长的分析与改进

参数Zuplimit控制着雇佣蜂和侦察蜂的角色转换.一个自适应的步长能够增强算法对问题的适应性［16］.当现有解的收益度很差时，应尽早放弃.如果改善缓慢的话，会拖延收敛速度.基本ABC算法中Zlimit的增长步长为1，为了能够根据解的质量动态调整其搜索次数，本文设定Zlimit的动态步长为

式中：fi为当前解的收益度；

fLbest为当前局部最优解的收益度，本文以平衡指标f2的值表示收益度.

由式（10）可知，若λ＜1，则表示新搜索到的解优于局部最优解，搜索进程放缓，搜索机会增加；若λ＞1，则表示新搜索到的解劣于局部最优解，搜索进程加速，对劣解的搜索次数减少.

3.3 观察蜂搜索策略改进

长距离的交换和插入操作很容易引起平衡指标的改变，导致危害指标和需求指标被忽视.蠕动搜索就是将有危害或高需求的任务向前做一个微小距离的移动，在保证平衡指标性能的前提下，提高后续目标函数的质量.

为了增强对危害目标和需求目标的搜索能力，使雇佣蜂执行雇佣蜂搜索和蠕动搜索两种搜索方式，以增大改善当前解的可能性.

3.4 侦察蜂搜索策略分析与改进

分布估计算法是进化算法的一种，其原理是基于概率模式的引导作用，即对历次搜寻到的较优个体集合建立概率模型，通过该模型对下一步的搜索范围进行引导.具体到人工蜂群算法中，局部最优解作为一组质量较好的解，可以作为构建指引侦察蜂搜索的经验信息库的基础.本文引入一个基于任务与位置对应的分布估计矩阵Q，该矩阵记录局部最优解中任务与位置对应关系在局部最优解中出现的频次，并以此作为引导侦察蜂进行全局搜索的标杆.

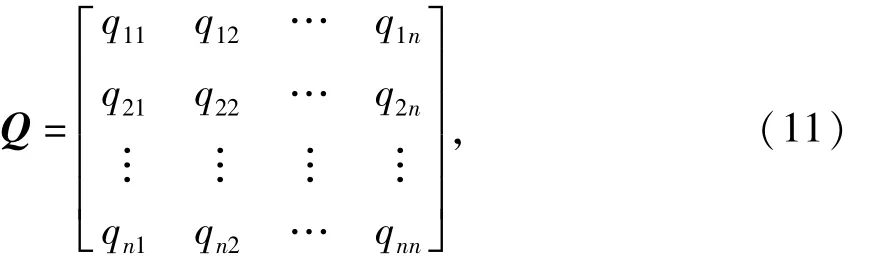
式中：qij为拆卸任务j在拆卸序列第i个位置上出现的次数，

i，j=1，2，…，n.

统计矩阵Q的初始数据取自于最优的初始解，对反映该解序列中任务与位置对应关系的元素qij进行加权处理，权值为α，解的平衡指标越小，说明任务所在位置越好.危害性指标和需求指标越小，说明有危害和高需求的零件被拆除的越早.为了反映对应关系在平衡性、危害性和需求指标上的质量，令越优的解其α值越大，设定

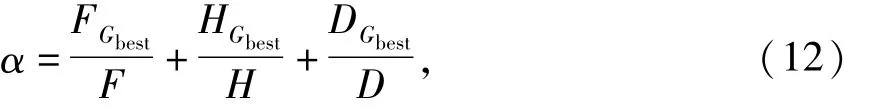
式中：F、H、D分别为解的平衡指标、危害指标和需求指标；带下标Gbest的量为当前全局最优解.

每当产生一个局部最优解，且该解的平衡指标不劣于当前全局最优解，就用该解更新矩阵Q.搜索初期获得的全局最优解质量较差，对应的矩阵Q质量也较差.

为了能随着搜索的深入逐渐削弱矩阵Q在前期受到的不良影响，根据测试经验，对矩阵Q引入衰减常数，衰减常数的值为0.8.

在侦察蜂搜索阶段，可行解的构造策略为：从可分配任务集Trang中按照式（13）计算出的任务选择概率进行任务的选择与分配.

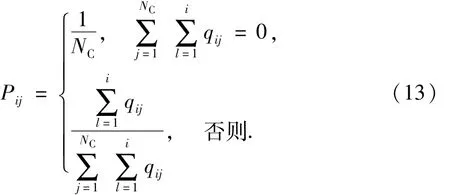
由式（13）可知，在对位置i进行任务分配时，集合Trang中每个任务被选择的概率是由前i处位置上该任务出现的概率之和决定的.换言之，若集合Trang中所有任务均未在前i处位置上出现过，则它们被选择的概率相同.

为了不失搜索的随机性，侦察蜂采用分布估计搜索和随机搜索两种策略.改进后的ABC算法流程图如图1所示.

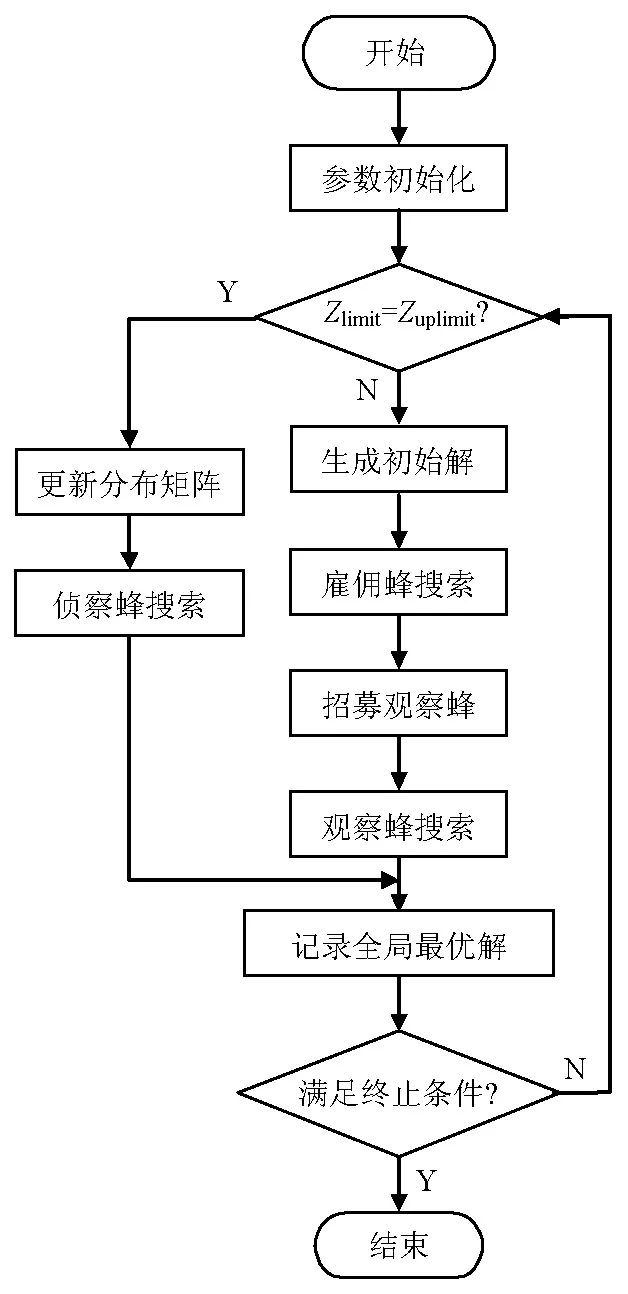
图1 改进ABC算法流程Fig.1 Flow chart of the improved ABC algorithm

4 算例测试与分析

4.1 测试问题

根据第3节改进ABC算法，用MATLAB R2008a编程实现，在Windows7系统下Intel Core 2.20 GHz CPU、2 GB RAM的计算机上，进行了多次试验计算.考虑到拆卸线平衡问题与装配线平衡问题（simple assembly line balancing problem，SALBP）结构相似，具有相同的优先关系、节拍约束等，两者均为NP问题，故衡量装配线平衡问题的性能在一定程度上也可体现求解拆卸线平衡问题的性能.首先，对SALBP测试问题集进行求解以验证算法的有效性.该基准测试问题集的相关数据可通过如下网址获取：http：//alb.mansci.de/files/

uploads/SALBP%20data%20sets.zip.设置算法参数如下：

雇佣蜂数目Neb=10；

最大搜索步长Zuplimit=10；

最大迭代次数M=50.

测试结果如表1所示.

表1给出用改进ABC算法求解不同规模、不同节拍的70个测试问题的解，对其中的65个问题求得了最优解，5个问题求出了比最优解多一个或两个工作站的近优解，算法的求解性能是可以接受的.

4.2 实例问题

实例1 对文献［7］中10个任务的拆卸实例进行求解，具体拆卸任务数据及优先关系如图2所示，圈中数字表示任务编号，*表示有危害性的任务；右上角数字表示拆卸任务的作业时间；左下角数字表示需求量.为使图2简洁，危害指标和需求指标为0的情况不予标注.

各项拆卸任务的作业时间（单位：s）

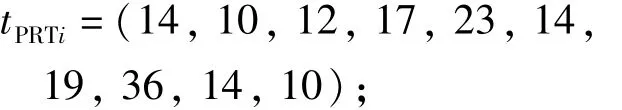
危害指标

需求指标

设置算法参数如下：雇佣蜂数量Neb=10，

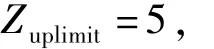
循环次数M=100.

表1 基准算例测试结果Tab.1 Performance comparison on benchmark problems

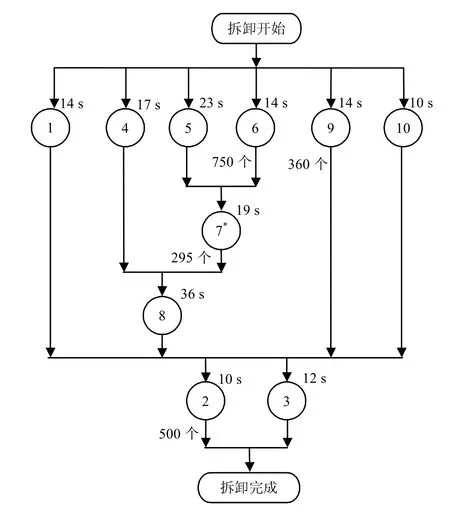
图2 拆卸任务数据及优先关系Fig.2 Precedence diagram and data of disassembly tasks

运行程序20次，每次均能很快找到最优解，所用时间平均为0.73 s.对比文献［7］用蚁群算法求解出的最优解目标函数值，结果如表2所示.

从表2可知，两种算法的工作站数、平衡和危害指标相同，在需求指标上ABC算法优于文献［7］算法.

用ABC算法所得最优解序列见表3，有危害和高需求的拆卸任务6、7、9被尽早完成，因为优先关系的缘故，有需求的任务2执行较晚，但仍在无需求的任务3之前被执行.说明了本文算法在观察蜂搜索阶段针对危害指标和需求指标采取的蠕动搜索策略是有效的.

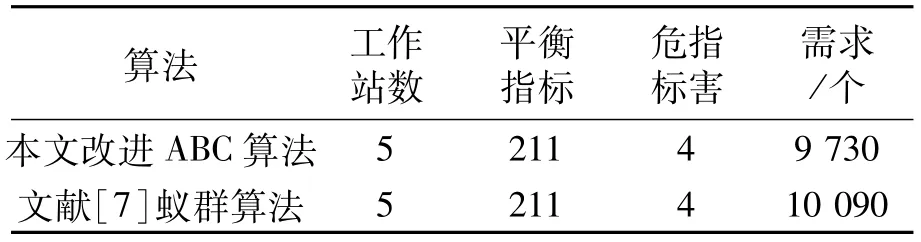
表2 算法求解结果对比Tab.2 Solution comparison of the two algorithms

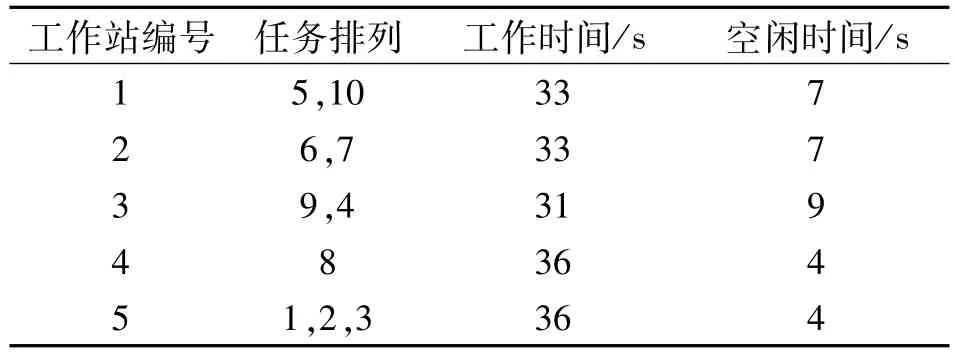
表3 10个任务实例的最优解Tab.3 Optimal solution for the 10-task case

图3是20次运行所得平衡指标的平均值收敛图.从图3可见平衡指标很快收敛于最优值211，收敛的最大循环次数不超过20次.该测试结果说明ABC算法在求解拆卸线平衡问题时的有效性.

实例2 对文献［5］中某企业52个任务的高速电子套结机拆卸实例进行求解，节拍时间为600 s.由于该问题模型中考虑了拆卸成本，为便于比较，将文献［5］中的平滑率指标函数Fsmooth以及拆卸成本函数Fcost引入本文算法，描述为

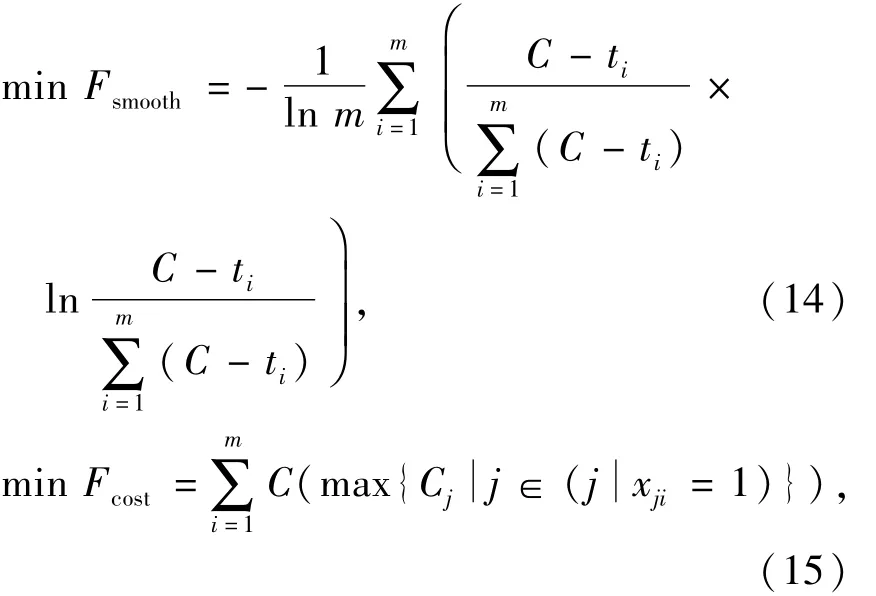
式中：Cj为拆卸任务j的单位时间拆卸成本.

图3 平衡指标收敛图Fig.3 Convergent graph of balance index

由于该案例含任务数较多，为加强对最优解的搜索能力，适当调高算法参数，设置雇佣蜂数量Neb=10，Zuplimit=8，循环次数M=200.将多次测试所得结果平均值与文献［5］的求解结果平均值进行了比较，见表4和图4.

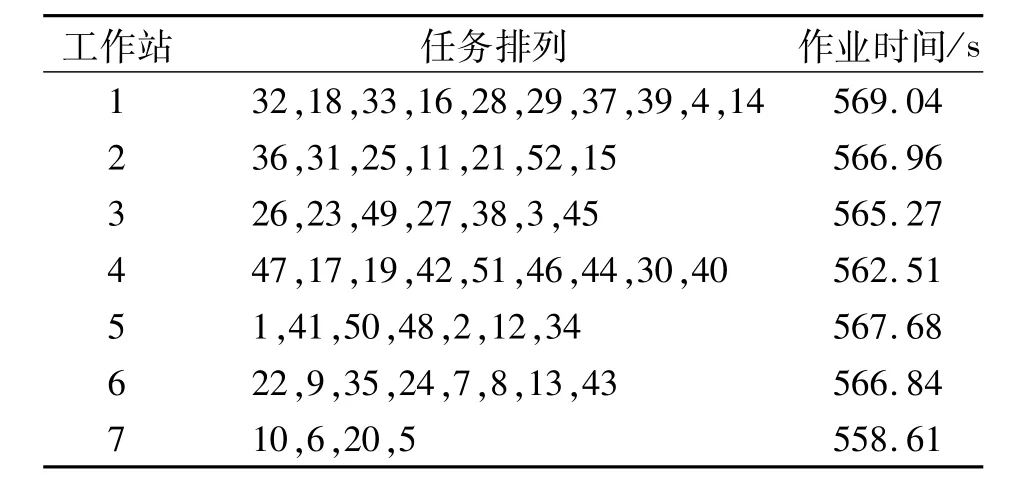
表4 套结机实例优化结果Tab.4 Optimal solutions for the bar tacking machine case

由图4可知，用本文改进ABC算法求出的开启工作站数目、平滑率、拆卸成本3项指标均优于文献［5］算法.

本文改进ABC算法得到最优分配结果如表4所示.由表4可知，在所有开启的工作站中，作业时间最大值为569.04 s，作业时间最小值为558.61 s，相差仅为10.43 s，相对于节拍时间600 s，时差比例仅为1.74%.因此，各工作站作业负荷基本处于均衡状态，由此说明了本文算法的优越性能.

图4 目标函数结果对比Fig.4 Result comparison of objective functions

5 结束语

针对传统算法在求解多目标DLBP问题时搜索过于随机、易早熟和易陷入局部最优等方面的不足，提出了一种改进的人工蜂群算法.在生成初始解时，考虑了任务的危害性和需求对初始解质量的影响，提高了初始解针对危害指标和需求指标的质量；在雇佣蜂阶段，用可变步长增加较优解的搜索机会，加速淘汰劣解；在观察蜂阶段，以微小的蠕动搜索提高解在危害性和需求方面的质量；在侦察蜂阶段，以分布估计矩阵引导搜索过程.通过大规模算例测试验证了算法的有效性.应用改进ABC算法求解电子套结机拆卸实例，取得了优良的求解效果.

下一步的研究方向可将改进ABC算法拓展应用到不确定时间拆卸及混合产品拆卸等DLBP问题中去.

［1］ GUPTA S M，GUNGOR A.Product recovery using a disassembly line： challenges and solution［C］∥Proceedings of the 2001 IEEE International Symposium on Electronics and the Environment. Colorado：［s.n.］，2001：36-40.

［2］ 张则强，胡俊逸，程文明.第Ⅰ类双边装配线平衡问题的改进蚁群算法［J］.西南交通大学学报，2013，48（4）：724-730.

ZHANG Zeqiang，HU Junyi，CHENG Wenming. Improved ant colony algorithm for two-sided assembly line balancing problem oftypeⅠ［J］. Journalof Southwest Jiaotong University，2013，48（4）：724-730.［3］ DUTA L，FILIP F G，CACIULA I.Real time balancing of complex disassembly lines［C］∥ 17th World Congress， International Federation of Automatic Control，IFAC.Seoul：［s.n.］，2008：913-918.

［4］ MCGOVERN S M，GUPTA S M.A balancing method and genetic algorithm for disassembly line balancing［J］. European Journal of Operational Research，2007，179（3）：692-708.

［5］ 丁力平，谭建荣，冯毅雄，等.基于Pareto蚁群算法的拆卸线平衡多目标优化［J］.计算机集成制造系统，2009，15（7）：1406-1429.

DING Liping，TAN Jianrong，FENG Yixiong，et al. Multiobjective optimization for disassembly line balancing based on Pareto ant colony algorithm［J］. ComputerIntegrated ManufacturingSystems，2009，15（7）：1406-1429.

［6］ LAMBERT A，GUPTA S M.Methods for optimum and near optimum disassembly sequencing［J］.International Journal of Production Research，2008，46（11）：2845-2865.

［7］ MCGOVERN S，GUPTA S.Ant colony optimization for disassembly sequencing with multiple objectives［J］. The International Journal of Advanced Manufacturing Technology，2006，30（5/6）：481-496.

［8］ 朱兴涛，张则强，朱勋梦，等.求解多目标拆卸线平衡问题的一种蚁群算法［J］.中国机械工程，2014，25（8）：1075-1079.

ZHU Xingtao，ZHANG Zeqiang，ZHU Xunmeng，et al. Ant colony optimization for multi-objective disassembly line balancing problem［J］. China Mechanical Engineering，2014，25（8）：1075-1079.

［9］ HEZER S，KARA Y.A network-based shortest route model for parallel disassembly line balancing problem［J］. International Journal of Production Research，2015，53（6）：1849-1865.

［10］ KALAYCI C B，POLAT O，GUPTA S M.A variable neighbourhood search algorithm for disassembly lines［J］. Journal of Manufacturing Technology Management，2015，26（2）：182-194.

［11］ KALAYCI C B，GUPTA S M.Artificial bee colony algorithm for solving sequence：dependent disassembly linebalancing problem［J］. ExpertSystems with Applications，2013，40（18）：7231-7241.

［12］ KARABOGA D.An idea based on honey bee swarm for numerical optimization In Technical report TR06［R］.Kayseri：Erciyes University，2005.

［13］ 傅继阳，钟亮，黄友钦，等.基于量子粒子群算法的门式刚架结构抗风优化［J］.西南交通大学学报，2013，48（5）：845-850.

FU Jiyang，ZHONG Liang，HUANG Youqin，et al. Wind-resistant optimization of portal frames based on quantum-behaved particle swarm algorithm［J］. JournalofSouthwestJiaotong University，2013，48（5）：845-850.

［14］ 宋荣荣，陈滋利.基于PSO算法的磁浮系统PID控制器优化与评价［J］.西南交通大学学报，2015，50（1）：36-43.

SONG Rongrong，CHEN Zili.Optimization and design of maglev system PID controller based on particle swarm optimization algorithm［J］.Journal of Southwest Jiaotong University，2015，50（1）：36-43.

［15］ KARABOGA D，GORKEMLI B，OZTURK C，et al. A comprehensive survey：artificial bee colony（ABC）algorithm and applications［J］.Artificial Intelligence Review，2014，42（1）：21-57.

［16］ ALAM M S，UL KABIR M，ISLAM M M.Selfadaptation of mutation step size in artificial bee colony algorithm for continuous function optimization［C］∥2010 13th International Conference on Computer and Information Technology（ICCIT）.［S.l.］：IEEE，2010：69-74.

求解拆卸线平衡问题的改进人工蜂群算法

张则强， 胡 扬， 陈 冲

Improved Artificial Bee Colony Algorithm for Disassembly Line Balancing Problem

ZHANG Zeqiang， HU Yang， CHEN Chong
（School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

The disassembly line balancing problem（DLBP）has been mathematically proved to be NP-complete.The search processes of traditional algorithms for DLBP are so random that they tend to get local optimum due to DLBP's exponential time complexity for large scale cases.To overcome the shortcomings of traditional algorithms，an improved artificial bee colony（ABC）algorithm was proposed based on a multi-objective optimization model for the DLBP，where the main objectives to achieve are to minimize the number of workstations，equilibrate workload，and remove hazardous and high-demand components as early as possible.This algorithm includes four phases.In the initial solution generation phase，the hazardous index and demand measure are used to improve the convergence property of the algorithm.In the employed bee phase，a variable step length search strategy is introduced to take a further search for better solutions and speed up the elimination of inferior solutions.In the onlooker bee phase，a hybrid search strategy that combines the traditional search with the disturbance search is adopted.In the scout bee phase，a search strategy based on estimation of distribution is constructed.The proposed algorithm was applied to solve 70 test cases to verify its validity.As a result，optimal solutions were obtained for 65 cases and the optimization rate is 92.86%.In addition，the algorithm was applied to solve a 10-task case and a 52-task case.The results show that the demand measures to obtain the optimal solution for the 10-task case are 9 730，which is 360 less that by ant colony optimization；meanwhile，better solutions for the balance rate，number of workstations and cost are obtained for the 52-task case.Compared to the traditional ABC algorithm，the improved algorithm has a significantly superior performance in solving large-scale DLBPs.

disassembly line balancing；artificial bee colony algorithm；optimization；disassembly

0258-2724（2016）05-910-08

10.3969/j.issn.0258-2724.2016.05.013

TH165

A

2015-05-04

国家自然科学基金资助项目（51205328）；教育部人文社会科学研究青年基金资助项目（12YJCZH296）；四川省应用基础研究计划项目（2014JY0232）

张则强（1978—），男，教授，博士，博士生导师，研究方向为制造系统与智能优化，E-mail：zzq_22@163.com

张则强，胡扬，陈冲.求解拆卸线平衡问题的改进人工蜂群算法［J］.西南交通大学学报，2016，51（5）：910-917.

（中文编辑：秦萍玲 英文编辑：兰俊思）