电活性聚合物圆柱壳的动力学特性分析

王成敏，任九生

（1.上海大学上海市应用数学和力学研究所，上海 200072；

2.上海大学理学院，上海 200444；

3.上海大学上海市力学在能源工程中的应用重点实验室，上海 200444）

电活性聚合物圆柱壳的动力学特性分析

王成敏1，任九生2，3

（1.上海大学上海市应用数学和力学研究所，上海 200072；

2.上海大学理学院，上海 200444；

3.上海大学上海市力学在能源工程中的应用重点实验室，上海 200444）

基于有限变形动力学理论,研究了电活性聚合物圆柱壳在内表面突加内压及电场作用下的运动与破坏问题.首先得到了描述电活性聚合物圆柱壳内表面运动的非线性常微分方程,然后对方程进行了数值计算并进行动力学定性分析.当突加内压小于某个确定的临界值时,圆柱壳产生非线性周期振动,而当突加内压大于这个临界值时,圆柱壳将被破坏.通过对振动的振幅、相图和周期的计算,讨论了外加电场、内压及圆柱壳的厚度等参数对圆柱壳振动情况的影响.

电活性聚合物；突加内压；非线性周期振动；临界载荷；破坏

电活性聚合物是一类新型智能材料，在电激励下可以发生较大应变，具有较高的机电转换效率.19世纪80年代机电响应现象被发现［1］，这是人类首次研究电活性聚合物.该类材料具有质量轻、易于成形、运动灵活、价格便宜和不易疲劳损坏等优点［2-4］，在机器人、医用、航空、航天等多个领域备受关注［5-7］.自20世纪90年代以来，众多国内外研究者对电活性聚合物性能、模型和应用开展了实验研究［8-10］.近10年来，电活性聚合物材料发展尤为迅速，一系列性能优异的电活性聚合物材料相继被开发出来，它的应用也日益广泛［11-12］.

电活性聚合物在静载下的力学特性在国内外得到广泛研究，但其在动载下的响应问题还有待深入探究.本研究的目的是通过分析电活性聚合物圆柱壳在突加内压作用下的运动及破坏问题，为其在工程中的应用提供一定的理论指导.本研究首先建立了问题的控制方程组，得到了描述电活性聚合物圆柱壳内表面运动的二阶非线性常微分方程，然后对方程组进行计算和动力学定性分析，求出方程解及振动的相图、振幅、周期等结果.通过对振动的振幅、相图和周期的分析，讨论了外加电场、内压及圆柱壳的厚度等因素对圆柱壳振动情况的影响.

1 问题的数学描述

考虑一个内径为A、外径为B、长度为L的不可压电活性聚合物圆柱壳（见图1），在初始时刻t=0时在内表面受到突加内压p（t），并在圆柱壳内外表面施加电场.设圆柱壳变形后其内径为a、外径为b、长度为l.分别取物质坐标系和空间坐标系为（R，Θ，Z）和（r,θ,z），则圆柱壳的运动模式为

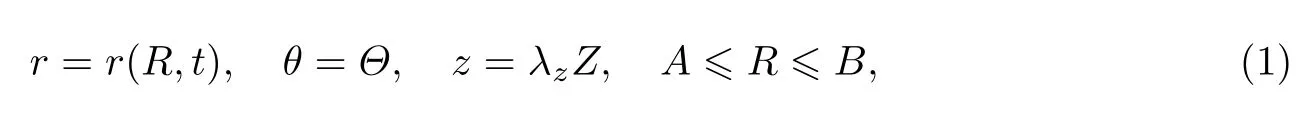
式中，r（R,t）为待定函数；轴向拉伸λz为圆柱壳预加应变限制，是一预先给定的常数.相应的变形梯度张量F为

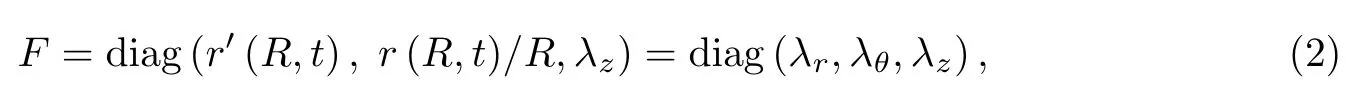
相应的圆柱壳主伸长

图1 变形前和变形后的圆柱壳结构Fig.1 Undeformed and deformed configurations of the cylindrical shell

由材料的不可压条件可得

于是

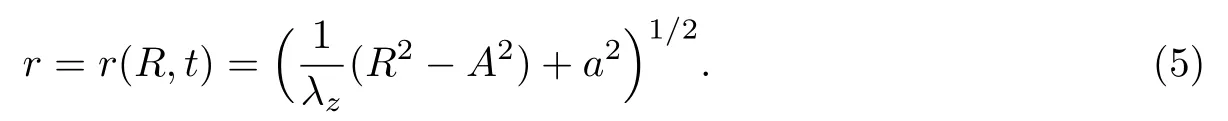
本研究考虑广义不可压Ogden电活性聚合物材料［13］，其应变能函数为

式中，ε为材料的介电常数，取ε=2.21×10-11F/m［14］；D为径向电位移.材料常数［15-18］

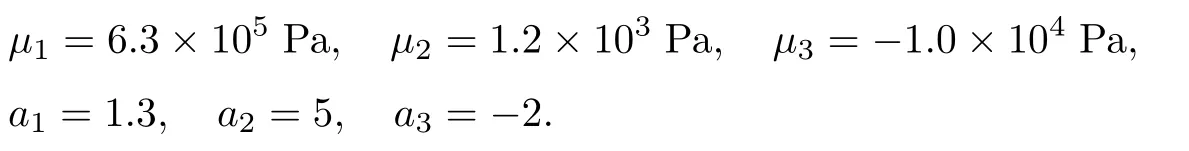
电活性聚合物的应力

式中，P（r,t）为静水压力.

对圆柱壳而言，电位移D和电势φ的关系为

圆柱壳的运动方程为

圆柱壳受突加内压作用的边界条件为

满足无约束自然状态的初始条件为

电场的边界条件为

2 问题的求解

由式（5）可得

将式（7）、（13）代入运动方程（9），并对r积分可得

将式（14）代入（7a），利用式（11a）可得P（a,t）=p（t）.代入式（11b）有

引入变换

令ξ=r/R，于是式（15）可改写为

其中

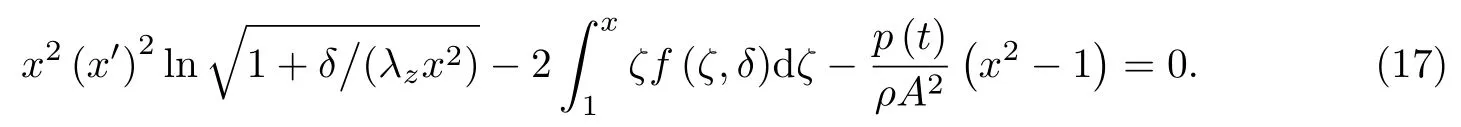
若存在x，使得如下函数

成立，则方程（17）有解.当突加载荷为常值时，即p（t）≡p时，方程（17）的解为

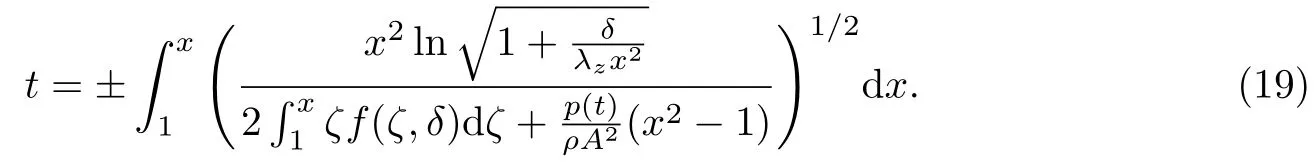
3 结果与讨论

为判定方程（16）是否有解，作出F（x,p）与x的关系曲线，不同参数下F（x,p）～x的关系曲线如图2～5所示.若方程（16）有解，则不同参数下不同载荷p对应的x值可根据

得到，记为xmax，xmax与载荷p的关系曲线如图6～8所示.图9给出了圆柱壳的时程曲线.由方程（17）可得到不同的xmax对应的速度与x的关系曲线，即运动的相图（见图10～13）.

图2 F（x,p）～x关系曲线（不同载荷）Fig.2 F（x,p）～x curves（different loads）

图3 不同壁厚下F（x,p）～x关系曲线Fig.3 F（x,p）～x curves for shells of different thicknesses

图4 不同电压下F（x,p）～x关系曲线Fig.4 F（x,p）～x curves for different voltages

图5 不同轴向拉伸下F（x,p）～x关系曲线Fig.5 F（x,p）～x curves for different axial stretches

从图1～4可以看出，对某一圆柱壳总是存在一个突加内压的临界载荷值pcr（当δ=1.04，λz=1.2，Φ=1.0×105V时，pcr约为1.1MPa）.

当p小于pcr时，F（x,p）～x曲线与x轴有（1，0）和（xmax，0）两个交点.当1＜x＜xmax时，F（x,p）＞0，当x＞xmax时，F（x,p）＜0，表明方程（17）有两个解x=1和x=xmax，圆柱壳可能会产生周期性运动.观察时程曲线（见图9）可见，在p＜pcr时圆柱壳的运动的确是周期性运动，其相图（见图10～13）是一条封闭的曲线.

而当p＞pcr时，F（x，p）＞0，F（x，p）～x曲线与x轴仅存在（1，0）一个交点，即方程（17）仅存在唯一解x=1，则圆柱壳的运动不是周期性运动.相图（见图10～13）也表明，当p＞pcr时，圆柱壳的相图不是封闭的曲线，证实了当p＞pcr时，圆柱壳不可能产生周期性运动.此时方程的解，即圆柱壳运动的幅值随时间的推移无限制地增大，表明随着时间的推移圆柱壳最终会被破坏.

图6 不同轴向拉伸下的振幅载荷关系曲线Fig.6 Amplitude and pressure curves for different axial stretches

图8 不同电压下的振幅载荷关系曲线Fig.8 Amplitude and pressure curves for different voltages

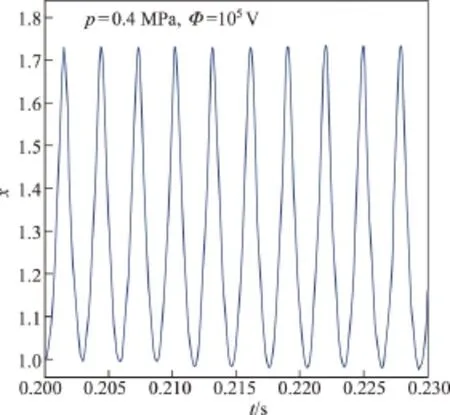
图9 圆柱壳时程曲线Fig.9 Oscillating response of cylindrical shell

圆柱壳发生周期振动的振幅就是曲线F（x,p）～x与x轴交点处的横坐标xmax.由相图10～13可见，在t=0时，x（0）=1，（0）=0，表明在初始时刻圆柱壳未变形，其初始速度为零.随着时间的推移，x逐渐增大，速度＞0，先增大然后逐渐减小；当x增大到最大值xmax时，速度减小到零；随着时间的继续推移，x逐渐减小，速度＜0，的绝对值先增大后减小，当x减小到1时，速度变为零，相图曲线～x闭合，圆柱壳的一个周期振动完成，然后进行周期性循环.

图6～8表明，圆柱壳周期性振动的振幅xmax随着内压p的增大而增大.同时图6也表明，当轴向拉伸增大时，振幅xmax减小，临界载荷pcr略微增大，可知轴向拉伸抑制圆柱壳周期性振动；图7表明，当圆柱壳厚度减小时，振幅xmax变大，临界载荷pcr变小，可知圆柱壳壁厚越薄，越容易发生破坏；图8表明，当外加电压增大时，振幅xmax变大，临界载荷pcr减小，表明外加电压促进了圆柱壳周期性振动.

图10 不同载荷下的相图Fig.10 Phase diagram for different loads

图11 不同壁厚圆柱壳的相图Fig.11 Phase diagram for shells of different thicknesses

图12 不同轴向拉伸下的相图Fig.12 Phase diagram for different axial stretches

图13 不同电压下的相图Fig.13 Phase diagram for different voltages

图10～13表明，当p＜pcr时，圆柱壳的相图是一条对称的封闭曲线，表明当p＜pcr时圆柱壳发生周期性振动；当p＞pcr时，圆柱壳的相图不是封闭的曲线，表明当p＞pcr时圆柱壳的运动不是周期性运动.由

求得不同的xmax对应的振动周期T.如当δ=1.04，λz=1.2，Φ=1.0×105V时，相应于p=0.40，0.45，0.48，0.50MPa的振动周期分别为6.38，5.60，5.12，4.86 ms.当δ=1.04，λz=1.2，p=0.7 MPa时，相应于Φ=0，1.0×105，1.5×105，2.0×105V的振动周期分别为6.84，6.95，7.13，7.68 ms.结果表明电活性聚合物圆柱壳发生周期振动时，振动周期随着突加内压的增大而减小，随外加电压的增大而增大.

4 结束语

本研究分析了在突加内压和外加电场作用下的不可压电活性聚合物圆柱壳的动力学特性，得到了描述电活性聚合物圆柱壳内表面运动的非线性常微分方程，通过计算和动力学定性分析发现，突加内压存在一个确定的临界值.当突加内压小于这个临界值时，圆柱壳内表面发生周期性的非线性振动；当突加内压大于这个临界值时，圆柱壳将被破坏.同时研究结果还表明：减小圆柱壳厚度，突加内压的临界值减小，周期性振动的振幅增大，即圆柱壳越薄，越容易被破坏；当外加电压增大时，临界载荷值也减小，周期性振动的振幅增大，即外加电压有促进振动的作用；圆柱壳发生周期性运动时，其振动周期随内压的增大而减小，随电压的增大而增大.

［1］BAR-COHEN Y.Electroactive polymers：current capabilities and challenges［J］.Spies International Symposium on Smart Structures and Materials,2002,4695：1-7.

［2］TANAKA Y，FUJIKAWA T，KAZOE Y,et al.An active valve incorporated into a microchip using a high strain electroactive polymer［J］.Sensors and Actuators B：Chemical,2013,184：163-169.

［3］PLANTE J S，DUBOWSKY S.Large-scale failure modes of dielectric elastomer actuators［J］.Int J of Solids and Structures,2006,43：7727-7751.

［4］SASIKALA S，MADHAVAN K T，RAMESH G,et al.The electro-mechanical performance of electroactive polymerbased actuators fabricated using ultra thin metal electrode［J］.Sensors and Actuators A：Physical,2014,207：43-48.

［5］LI M，JIANG Z Y，WANG P F,et al.Control of a quadruped robot with bionic springy legs in trotting gait［J］.Journal of Bionic Engineering,2014,11（2）：188-198.

［6］张冬至,童俊,刘哲,等.基于电活性聚合物薄膜柔性器件的触觉传感特性［J］.光学精密工程,2014, 22（8）：2151-2158.

［7］KRISHEN K.Space applications for ionic polymermetal composite sensors,actuators,and artificial muscles［J］.Acta Astronautica,2009,64（11/12）：1160-1166.

［8］宿丹,第凤,邢季,等.导电聚合物在药物可控释放领域的应用［J］.化学进展,2014,26（12）：1962-1976.

［9］李洋,孙楫舟,王晋芬,等.基于电流脉冲沉积法的硝酸根微传感器研究［J］.分析化学研究报告, 2015,43（1）：98-104.

［10］MAJIDI C，SHEPHERD R F，KRAMER R K,et al.Influence of surface traction on soft robot undulation［J］.The International Journal of Robotics Research,2013,32（13）：1577-1584.

［11］MAAS J，GRAF C.Dielectric elastomers for hydro power harvesting［J］.Smart Materials and Structures,2012,21（6）：064006.

［12］BROCHU P，QIBING P.Advances in dielectric elastomers for actuators and artificial muscles［J］. Macromol Rapid Comm,2010,31（1）：10-36.

［13］GOULBOURNE N C，MOCKENSTURM E M，FRECKER M I.Electro-elastomers：large deformation analysis of silicone membranes［J］.Int J Solids Struct,2007,44（9）：2609-2626.

［14］D´ıAZ-CALLEJA R，RIANDE E，SANCHIS M J.On electromechanical stability of dielectric elastomers［J］.Appl Phys Lett,2008,93（10）：101902.

［15］何新振,雍华东,周又和.电活性聚合物圆柱壳静态与动态电压下的的响应及稳定性［J］.固体力学学报,2012,33（4）：341-347.

［16］任九生,程昌钧.受内压热超弹性球壳的不稳定性［J］.上海大学学报（自然科学版）,2007,13（6）：732-735.

［17］任九生,周琎闻,袁学刚.钢丝编织高压胶管的力学性能及破坏强度［J］.上海大学学报（自然科学版）,2009,15（6）：644-648.

［18］RUDYKH S，BHATTACHARYA K，DEBOTTON G.Snap-through actuation of thick-wall electroactive balloons［J］.Int J of Non-Linear Mechanics,2012,47：206-209.

本文彩色版可登陆本刊网站查询：http：//www.journal.shu.edu.cn

Dynamic analysis of electro-active polymer cylindrical shells

WANG Chengmin1，REN Jiusheng2,3
（1.Shanghai Institute of Applied Mathematics and Mechanics，Shanghai University，Shanghai 200072，China；
2.College of Sciences，Shanghai University，Shanghai 200444，China；
3.Key Laboratory of Mechanics in Energy Engineering，Shanghai University，Shanghai 200444，China）

Based on the theory of finite elasto-dynamics,motion and destruction of an electro-active polymer cylindrical shell subject to suddenly applied internal pressure and an electric field are studied.A nonlinear differential equation describing the motion of the shell's inner surface is developed.Numerical computation and qualitative dynamic analysis are conducted.It is shown that nonlinear periodic oscillation exists when the internal pressure is less than a critical value.When the pressure exceeds the value,the shell is destroyed.The effects of electric field,internal pressure and thickness of the shell on oscillation are discussed by examining vibration amplitudes,phase diagrams and periods.

electro-active polymer；suddenly applied internal pressure；nonlinear periodic oscillation；critical pressure；destroy

O 343.5

A

1007-2861（2016）04-0486-11

10.3969/j.issn.1007-2861.2014.05.022

2014-11-28

上海市重点学科建设资助项目（S30106）

任九生（1970—），男，教授，博士，研究方向为固体力学.E-mail：jsren@shu.edu.cn