半参数顺序变量回归模型
2016-10-20熊笛何幼桦
熊笛,何幼桦
(上海大学理学院,上海 200444)
半参数顺序变量回归模型
熊笛,何幼桦
(上海大学理学院,上海 200444)
在比例优势模型基础上对顺序变量回归模型作更一般的推广,建立了半参数顺序变量回归模型,构造了模型中的线性和非线性部分的估计量,并证明了该估计量的弱相合性.通过数值模拟,考察了不同样本容量下半参数顺序变量回归的判断正确率和回归函数的均方误差.实验结果表明:半参数顺序回归模型在小样本情况下仍具有较高精度,并且在实验点处的重复次数相对于观察点个数对精度影响更大.通过对粮食预警实例的计算表明,半参数顺序回归模型较比例优势线性模型具有更好的外推效果.
比例优势模型;顺序变量回归;半参数回归
顺序变量是用于说明事物有序类别或者有序等级的一类以顺序数据作为具体表现的变量,也是0,1二分类变量的扩展,广泛出现在各应用领域的统计模型中.1959年Duncan[1]根据非相关选择项的独立性(independence from irrelevant alternation)特性首次提出了logit模型,该模型也是最早的离散因变量回归模型.Cox[2]提出了0,1二分类logit模型,并对二分类变量回归的线性模型形式进行了详细的分析.此后,自变量为数值变量、响应变量为顺序变量的多分类顺序变量回归问题被深入讨论与研究.
设响应变量Y为K个类别的顺序变量,通过顺序值1,2,…,K表征响应变量所归属的类别或等级.若对于d维解释变量X,响应变量Y属于第j类的概率为pj(x)=P(Y=j|x=x),j=1,2,…,K,那么,响应变量属于第j类的累积概率可以表示为

可以按概率γj(x)和1-γj(x)把K个等级分成{1,2,…,j}和{j+1,j+2,…,K}两类,在此基础上以γj(x)/(1-γj(x))表示顺序变量Y所属级别或等级不大于j(Y 6 j)时的优势比.把{1,2,…,j}和{j+1,j+2,…,K}两类视为一种两个类别的数据形式,在Cox[2]的二分类logit模型基础上得到了更一般的多类别模型:
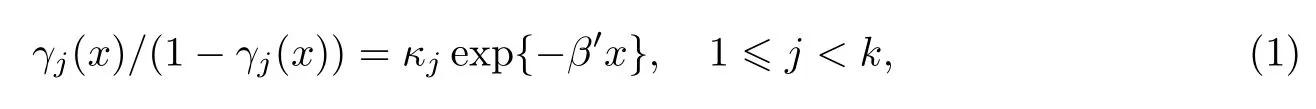
或以线性模型形式

式中,θj=lgκj为第j个等级的基准线.模型(1)为McCullagh[3]在1980年提出的比例优势模型(有序logit模型),它是二分类logit模型的扩展.如果当响应变量只有两类时,则比例优势模型就是一个线性logit模型.
目前,比例优势模型成为顺序变量回归的主流方法之一.Pettitt[4]把比例优势模型应用于生存数据研究中,并对比例优势模型的估计方法进行了讨论;Murphy等[5]研究了极大似然估计方法在比例优势模型上的运用;Ibrahim等[6]对该模型在贝叶斯变量上的选择方式进行了分析;Lang[7]导出了顺序回归模型中混合连接函数的贝叶斯估计方法;Lam等[8]提出右删失数据的比例优势模型的极大似然估计方法.国内对该类模型的应用问题也有较多的研究,如文献[9-10]对二分类logit模型应用的正确性进行了探讨,并将比例优势模型应用于航空领域的加速寿命试验[11]、医药等[12]研究领域.
在很多实际问题中,自变量与因变量之间并不完全满足线性关系,因此仅用线性回归模型不能准确地描述所讨论的问题.在20世纪80年代中期,Engle等[13]提出了半参数(或称为偏线性)模型:

式中,因变量u受到一些控制变量y∈Rp和x∈Rq以及随机扰动ε的影响,并且x对u的影响是线性的;f(·)为未知函数;β=(β1,β2,…,βq)T为未知参数;ε|(x,y)~(0,σ2)是随机扰动的,在很多情况下可以假设它是正态的.
因此,顺序变量与影响因子之间的关系可以有更精细的描述.本研究考虑用一个连续非线性函数代替式(1)中的线性部分:
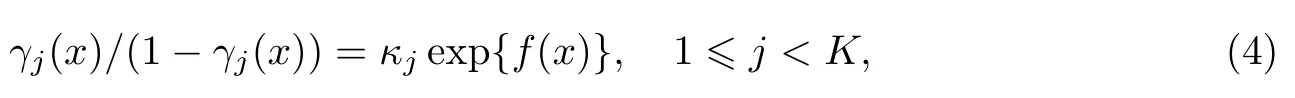
等式两边同时取对数,得到半参数顺序变量回归模型:

式中,θj=lgκj为第j个等级的基准线,且θj<θj+1,不失一般性,可设θ1=0.
1 半参数顺序回归模型的估计
令X为d维解释变量,Y是顺序响应变量,Y=j(j=1,2,…,K)表示响应变量归属于K个顺序类别中的第j个类别.
针对样本观察值(xi,Yi),Yi=Y(xi)∈{1,2,…,K},i=1,2,…,n.记Rij=Rj(xi)= #{xi|Y(xi)6 j},通过加权光滑方式得到γj(xi)的估计量
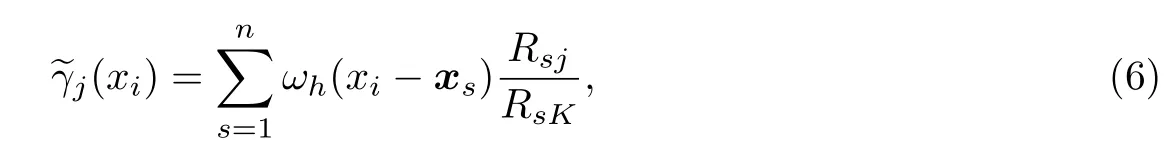
(2)ω(-x)=ω(x);
那么,lg(γj(xi)/(1-γj(xi)))的估计则可以表示为则半参数顺序回归模型(5)的样本模型为

对于扰动项,假设在给定j的情况下,{εij}~(0,σ2).
定理1 对于半参数顺序回归模型(5)中各θj的最佳线性无偏估计量为

证明 根据式(7),有
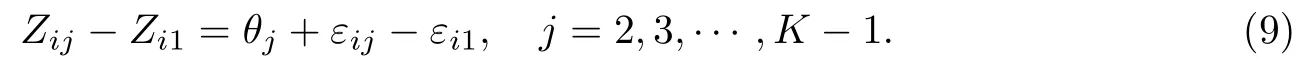
对于给定j,令ηj=εij-εi1~(0,Var(ηj)),根据最小二乘估计的基本结论,式(9)中各θj的最佳线性无偏估计为

注意到RijRi(j+1),且对于每一个j=1,2,…,K-1,至少存在一个i使得Rij<Ri(j+1)(否则第j类和第j+1类可合并为一类),故

于是有

在根据定理1得到θj的估计量后,记

于是有关于f(x)的非参数回归样本模型:

将参数和非参数部分的估计代回式(5)得到



证明 首先,对于每一个j=1,2,…,K-1,根据大数定律,式(8)中的按概率收敛到θj,即

其次,根据局部线性回归估计的残差定理[14]:
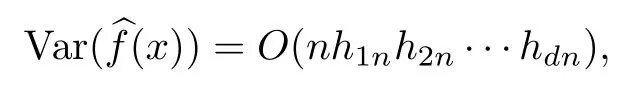
得到

当定理条件得到满足时,有
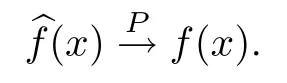

那么当X=x时,响应变量Y属于第j个类别的隶属概率的估计为
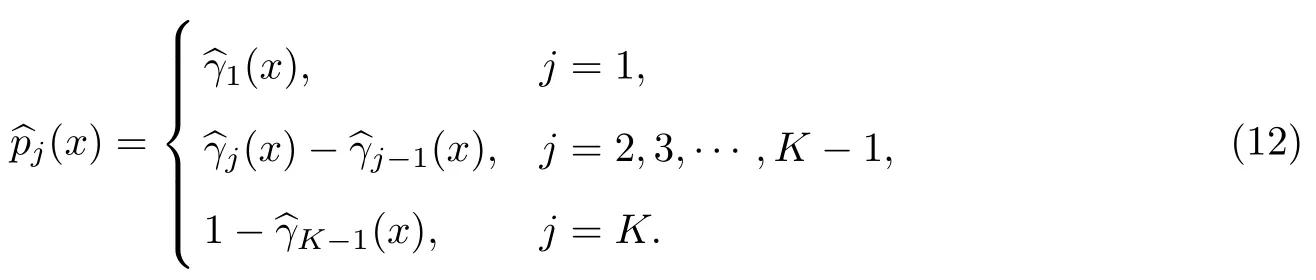
定义记

则称
本研究采用判断正确率(correct rate,CR)和均方误差(mean squared error,MSE)两个指标作为估计结果优良性的评判标准.
2 数值模拟
设定一个函数作为原始模型进行数值模拟,随机产生一系列实验样本点,然后利用这些样本数据对半参数顺序回归进行估计.
重复N次如下试验:
步骤1 随机产生n个解释变量值x1,x2,…,xn,在每个xi处对Y重复m次观察,共产生m×n组样本;
步骤2 利用半参数顺序回归模型中的式(12),计算

根据上述步骤得到的结果计算出半参数顺序回归模型判断正确率和均方误差两个指标:

(1)固定实验观察点个数n=30,改变在每个xi处对Y重复观察次数m=1,2,5,将得到的判断正确率CR(x)和均方误差MSE(x)的数值进行比较,结果如图1所示.
(2)固定每个xi处重复次数m=1,改变实验观察点个数n=30,100,将得到的判断正确率CR(x)和均方误差MSE(x)数值进行比较(见图2).
(3)固定实验样本容量m×n=60,讨论n=60,m=1,n=30,m=2以及n=20,m=3这3种情况,将得到的判断正确率CR和均方误差MSE数值进行比较(见图3).
实验结果表明:
(1)当实验观察点个数n不变时,每个xi处重复次数(m)越多,判断正确率就越高,回归函数的均方误差越小;
(2)当每个xi处重复次数m不变时,实验观察点个数(n)越多,判断正确率越高,回归函数的均方误差越小;
(3)当实验样本容量m×n不变时,在每个xi处重复次数(m)对判断正确率和回归函数的均方误差两个指标的影响比观察点个数n对它们的影响相对更大,即在样本容量相同的情况下,实验点xi处重复次数(m)越多,判断正确率就越高,回归函数的均方误差越小;
(4)当x靠近样本集边界时,判断正确率和回归函数的均方误差两个指标均不如x位于样本集内部时的情形,此时判断正确率相对更低,回归函数的均方误差相对较大.

图1 判断正确率CR和均方误差MSE(n=30,m=1,2,5)Fig.1 CR and MSE(n=30,m=1,2,5)

图2 判断正确率CR和均方误差MSE(m=1,n=30,100)Fig.2 CR and MSE(m=1,n=30,100)

图3 判断正确率CR和均方误差MSE(n=60,m=1和n=30,m=2以及n=20,m=3)Fig.3 CR and MSE(n=60,m=1 and n=30,m=2 and n=20,m=3)
3 半参数顺序变量回归模型的应用
作为一个应用实例,对粮食预警问题建立一个半参数顺序变量回归模型,将影响粮食价格波动的警源作为解释变量,对粮食警情等级进行预报.
将1978—2012年的粮食价格作为研究对象,取其价格相对变动作为粮食价格警情的指标.以当年粮食播种面积增长率、当年粮食亩产增长率、当年受灾面积增长率作为影响当年粮食价格波动的警源(样本数据见附录).
对于警情则采用多数原则,即把计算得到的粮食波动率数值从小到大排列,从第一个数据开始,将占总数2/3的数据作为安全警限,即无警警限,依次在剩下的波动率数据中划分轻警、中警、重警、巨警,根据实际划分情况,本研究将余下4个警限按照等距划分并依次将这5个警级命名为警级1,2,3,4,5.因此依据附录中粮食价格波动情况,结合多数原则将粮食价格警度进行划分(见表1)[15].

表1 多数原则下的粮食价格警度警限Table 1 Grain price warning degree under principle of majority
首先取1978—2012年数据作为样本点用半参数顺序回归模型进行内插检验,其判断正确率为100%.再以1978—2007年数据为训练样本,用比例优势线性模型和半参数顺序回归模型对2008—2012年粮食警级进行外推,判断正确率分别为60%和100%(见表2和3).

表2 顺序回归线性模型外推粮食价格警级结果Table 2 Extrapolation of grain price warning degree using ordinal regression linear model

表3 半参数顺序回归模型外推粮食价格警级结果Table 3 Extrapolation of grain price warning degree using semi-parametric ordinal regression model
4 结束语
本研究所建立的半参数顺序变量回归模型是在传统的线性顺序变量回归模型基础上考虑了非线性部分,扩展了模型的实际应用范围.同时,本研究通过半参数顺序回归模型对粮食价格进行了预警,从预警结果来看半参数顺序回归模型具有很好的预测效果.后续工作将从以下两个方向进行:①对于γj(x)估计的改进.当在每一个x处重复观察一次或很少时,所采用的估计方法(6)会有较大的误差,这个误差直接影响了模型估计的最终效果.②研究模型(4)基准量κj的一般化问题.如假设κj依赖于其他外生变量或与解释变量X有一定相关性,则整个估计方法会有较大的改变,模型的适用范围可以更大.
附录
表4中各项波动率、增长率是根据历年的统计年鉴(http://data.stats.gov.cn/workspace/ index?m=hgnd)计算得到的.

表4 1978—2012年粮食数据表Table 4 1978—2012 grain's data%
[1]DUNCAN L R.Individual choice behavior:a theoretical analysis[M].New York:John Wiley& Sons,1959.
[2]COx D R.The analysis of multivariate binary data[J].Royal Statistical Society,1972,21(2):113-120.
[3]MCCULLAGH P.Regression models for ordinal data[J].Journal of the Royal Statistical Society, 1980,42(2):109-142.
[4]PETTITT A N.Inference for the linear model using a likelihood based on ranks[J].Journal of the Royal Statistical Society,1982,44(2):234-243.
[5]MURPHY S A,ROSSINI A J.Maximum likelihood estimation in the proportional odds model[J]. Journal of the American Statistical Association,1997,92(439):968-976.
[6]IBRAHIM J G,CHEN M H,MACEACHERN S N.Bayesian variable selection for proportional hazards models[J].The Canadian Journal of Statists,1999,27(4):701-717.
[7]LANG J B.Bayesian ordinal and binary regression models with a parametric family of mixture links[J].Computational Statistics&Data Analysis,1999,31(1):59-87.
[8]LAM K F,LEUNG T L.Marginal likelihood estimation for proportional odds models with right censored data[J].Lifetime Data Analysis,2001,7(1):39-54.
[9]冯国双,陈景武,周春莲.logistic回归应用中容易忽视的几个问题[J].中华流行病学杂志,2004, 25(6):544-545.
[10]赵宇东,刘嵘,刘延龄.多元logistic回归的共线性分析[J].中国卫生统计,2001,17(5):259-261.
[11]黄婷婷,姜同敏.基于比例危险-比例优势模型的加速寿命试验设计[J].北京航空航天大学学报, 2010,36(5):570-579.
[12]唐俐玲,翟晓红.累积比数logit模型在有序资料中的正确应用[J].徐州医学院学报,2010,30(9):577-579.
[13]ENGLE R F,GRANGER C W J,RICE J,et al.Semiparametric estimates of the relationship between weather and electricity sales[J].Journal of the American Statistical Association,1986, 81(394):310-320.
[14]RUPPERT D,WAND M P.Multivariate locally weighted least squares regression[J].The Annals of Statistics,1994,22(3):1346-1370.
[15]吴璇.中国粮食价格预警系统研究[D].北京:中国农业大学,2003.
Semi-parametric ordinal variable regression model
XIONG Di,HE Youhua
(College of Sciences,Shanghai University,Shanghai 200444,China)
Based on a proportional odds model,the ordinal variable regression model is generalized,a semi-parametric ordinal regression model is established,and consistency of the estimators both in linear and nonlinear parts are proved in this paper.Simulation is conducted to analyze the correct rate and mean square error in the semi-parametric ordinal variable regression model with different sample sizes.The result shows that the semi-parametric ordinal regression model has high accuracy even with small samples.Compared to the number of observation points,the repeat number of experimental points has greater influence on accuracy.Calculation of the grain price warning problem shows that the semi-parametric ordinal regression model provides better extrapolation results than the proportional odds model.
proportional odds model;ordinal variable regression;semi-parametric regression
O 212
A
1007-2861(2016)04-0477-09
10.3969/j.issn.1007-2861.2014.04.010
2014-11-21
国家自然科学基金资助项目(11371242)
何幼桦(1960—),男,教授,博士,研究方向为概率统计.E-mail:heyouhua@shu.edu.cn
