青藏铁路轨道不平顺谱研究

陈宪麦，徐磊，王卫东，贺天龙，张向民，向尚，陈文韬

(1.中南大学 土木工程学院，湖南 长沙 410075；2.高速铁路建造技术国家工程实验室，湖南 长沙 410075；3. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031)



青藏铁路轨道不平顺谱研究

陈宪麦1,2，徐磊3，王卫东1，贺天龙1，张向民1,2，向尚1，陈文韬1

(1.中南大学 土木工程学院，湖南 长沙 410075；2.高速铁路建造技术国家工程实验室，湖南 长沙 410075；3. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

利用较为完备的青藏铁路轨道不平顺实测数据，将概率论方法较为系统的用于青藏铁路轨道不平顺谱研究，对不同波长的功率谱密度样本进行广义极值分布函数拟合、参数估计及假设检验分析。在此基础上，对青藏铁路的线路几何状态及轨道不平顺谱线特征进行分析；采用Levenberg-Marquardt法及铁科院7参数公式对青藏铁路轨道不平顺统计平均值谱进行公式拟合及参数提取；结合广义极值分布函数的参数估计值，提出由轨道不平顺统计平均值谱向任意百分位谱转换的方法。研究结果表明：青藏铁路轨道不平顺不同波长下的谱密度值均服从广义极值Ⅱ型分布(Frechet分布)；轨道高低和轨向不平顺谱线呈现复杂的窄带和周期波谱特征，其轨距不平顺状态基本处于德国高干扰谱和美国六级谱之间，应该作为重点关注的不平顺类型；结合不同波长谱密度的概率分布规律，建议在统计平均值谱的基础上，融合尖峰谱线特征，以便提供更为合理的动力仿真激励输入谱。

青藏铁路；轨道不平顺谱；广义极值分布；参数估计；假设检验；拟合

青藏铁路为世界上海拔最高、线路最长的高原铁路，受多年冻土影响，其对轮-轨动力相互作用更为敏感，线路基础结构的稳定与维护问题极具研究价值。现阶段，对于青藏铁路不同关键科学问题的研究已取得较为丰硕的成果，特别是冻土路基温度场、动力学等问题的研究受到普遍关注[1-7]。目前，对于青藏铁路轨道不平顺谱的系统研究还较少，轨道不平顺谱(track irregularity power spectrum density, PSD)既是轮轨系统之激励输入，也是线路基础结构几何状态的重要表征，在车辆-轨道耦合动力学分析与评估、机车车辆悬挂参数及线桥隧设计中十分重要。目前，美、德、英、法、日等国均已提出了相应速度范围的轨道不平顺标准谱[8-9]。国内学者也对轨道不平顺谱进行了长期的研究，陈宪麦等[10-11]对我国干线铁路轨道谱进行了研究，并提出了相应的轨道平顺性评判方法；练松良等[12-13]对多条线路的轨道不平顺谱进行了特征分析，提出了特征不利波长提取方法；李再帏等[14]利用上海轨道交通3号线轨道不平顺谱，与国内外标准谱进行了比较研究；徐磊等[15]对朔黄重载铁路的轨道不平顺谱进行了分析；康熊等[16]系统提出了我国高速铁路无砟轨道谱的计算方法、拟合公式及计算谱图，为高速铁路设计、评估和养护维修等提供了依据；黄连成[17-18]研究了青藏铁路轨道不平顺变化特征，并分析了无缝线路试验段轨道不平顺功率谱特征。

轨道不平顺作为一个随机过程，其不同波长下的功率谱密度也应该是随机分布的。对于随机问题，宜采用概率方法，特别是对于轨道不平顺标准谱的制定，不同波长标准谱密度的统计规律、概率水平及对应的动力特性等问题都需深入研究。基于此，本文利用较为完备的青藏铁路轨道不平顺实测数据，以概率论为基础，对青藏铁路的轨道不平顺谱特征，谱密度分布概型、估计参数及假设检验，轨道不平顺谱拟合，以及不同概率水平下的谱密度反演方法等问题做了较为系统的研究。

1　广义极值分布

20世纪初，Fisher与Tippett证明当取样足够长时，任何一个分布函数F(x)，上极限分布H(x)必收敛为与原始分布有关的三种形式[19]：

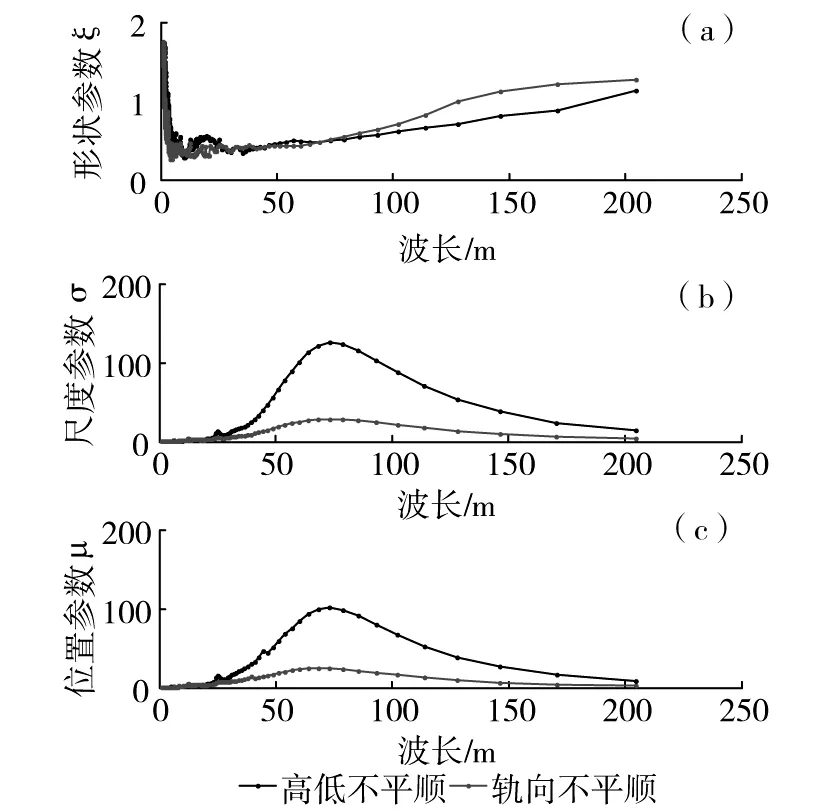
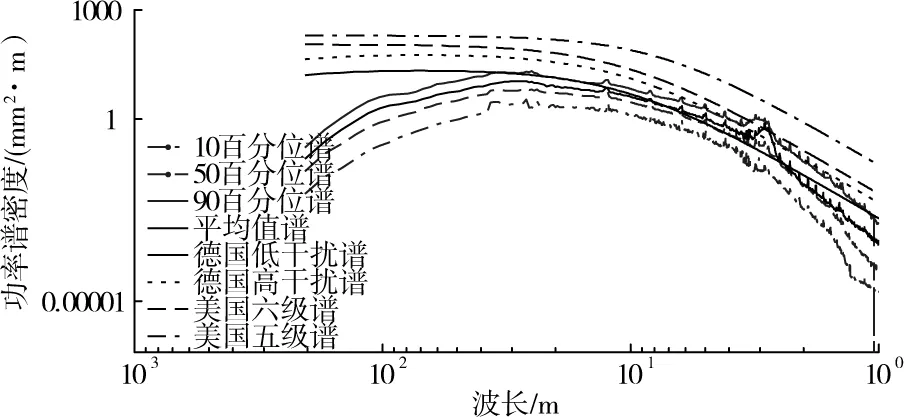
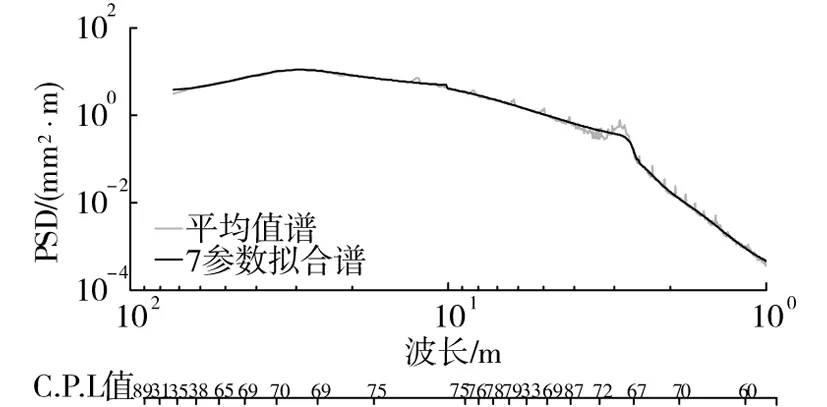
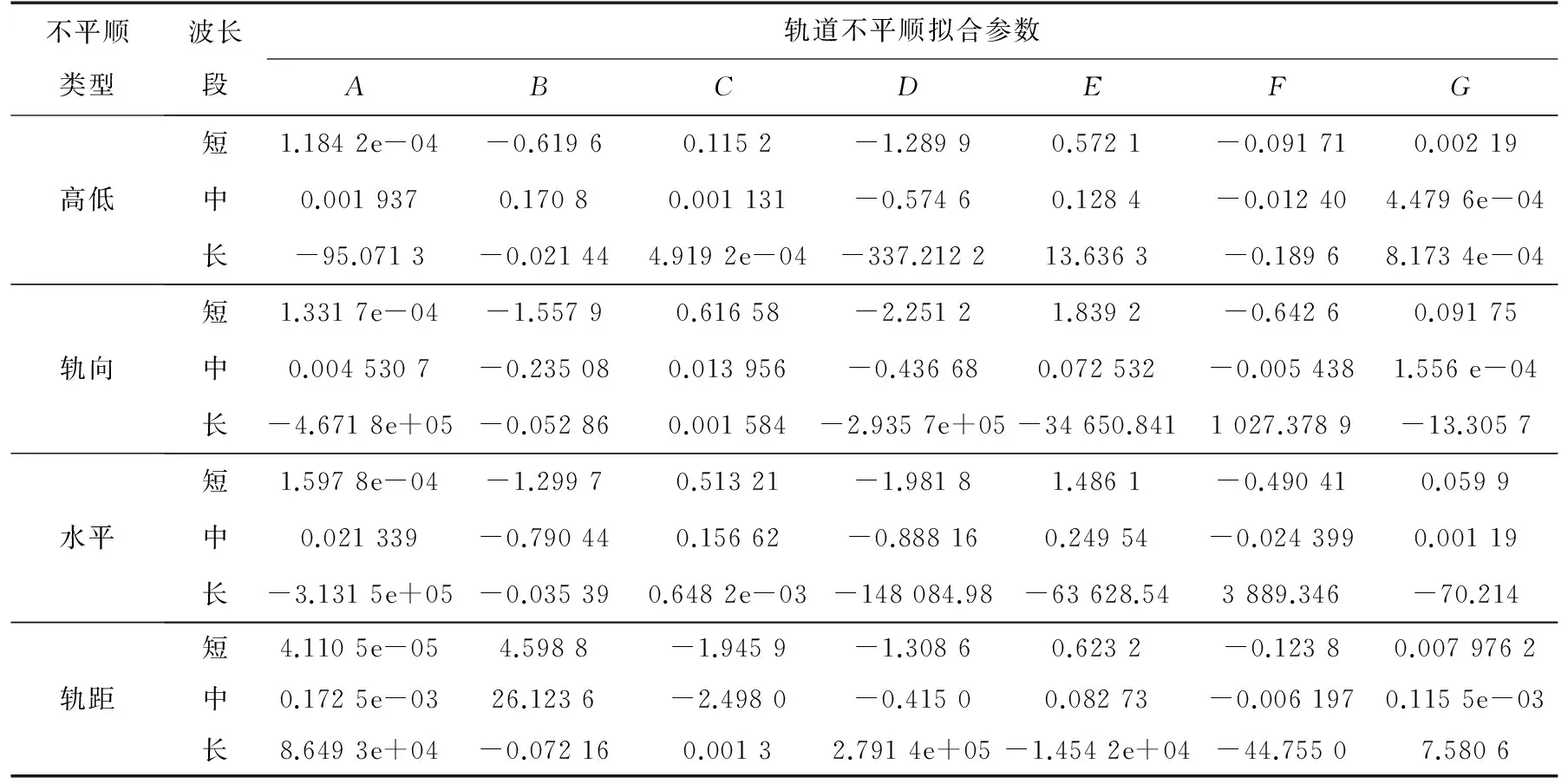
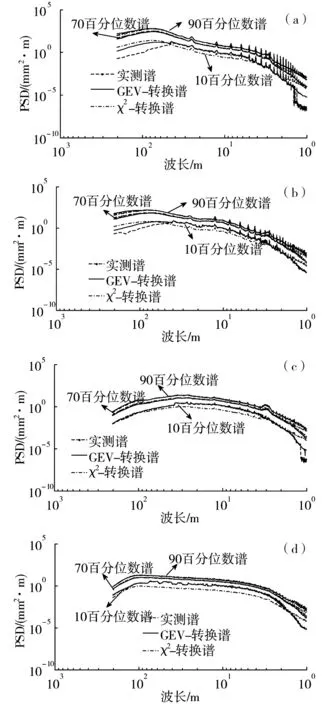
Ⅰ型分布：H1(x)=exp(-e-x)，-∞

Ⅱ型分布：

Ⅲ型分布：

极值Ⅰ型又称Gumbel分布、极值Ⅱ型又称Frechet分布、极值Ⅲ型又称Weibull分布。引入位置参数和尺度参数，则统一为广义极值分布[20-21]，其分布函数为：

(1)

式中：μ和σ分别为位置参数和尺度参数；ξ为形状参数；I(x)为示性函数，即

(2)

当ξ=0时，为Gumbel分布，即极值Ⅰ型；当ξ>0时，为Frechet分布，即极值Ⅱ型；当ξ<0时，为Weibull分布，即极值Ⅲ型。在计算得到分布函数参数后，可根据给定的概率水平H′求解对应的逆函数：

(3)

2　参数估计及假设检验方法

2.1极大似然参数估计方法

极大似然估计的基本思想是选择待定参数使样本出现在观测值的领域内的概率最大，并以这个作为未知参数的点估计值[22]。设ζ的分布是连续型的，密度函数f(x,θ1,θ2,...,θk)的形状已知，但含k个未知参数θ1,θ2,...,θk，以ζ1，ζ2，...,ζn分别带入其中的x，所得n个函数相乘而得函数[21]

(4)

(5)

解方程组式(6)，即可获得参数估计值

(6)

由于广义极值分布将3种极值分布统一在一起，不必考虑原始分布类型，参数估计可以采用同样的方法计算。若轨道不平顺的不同频率点谱值{s1,s2,...,sn}相互独立且具有相同概率分布，其参数的极大似然估计可通过下列对数似然函数求得

L(θ)=L(μ,σ,ξ)=

(7)

2.2非参数假设检验

本文采用χ2拟合优度检验法，用以样本数据是否服从指定的理论分布。对于假设H：“ξ的分布函数F(x)为F0(x)”，F0(x)为某已知分布函数。若H正确，令pi=F0(xi)-F0(xi-1)，根据皮尔逊(Pearson)定理[23]:

(8)

(y>0)，为χ2(m-1)分布的密度函数；N为样本总数；m为子区间数；vi为不同区间的样本数。

3　青藏铁路轨道不平顺谱特征分析

3.1数据来源

本文数据来源于青藏铁路2009-10～2014-7约27次轨检车实测数据，采样间隔为0.25 m。首先按文献[16]方法进行数据预处理，然后采用周期图法，每4 096点(1 024 m)计算一个轨道不平顺谱，不同不平顺类型的计算样本数见表1。

表1不同轨道不平顺类型的谱计算样本数

Table 1 Number of calculation samples for different types of track irregularities

不平顺类型左高低右高低左轨向右轨向扭曲水平轨距计算样本总数27280273082698826968276652998029980

3.2青藏铁路轨道不平顺谱的概率分布特征

3.2.1概率分析方法

本文对有效波长(段)下每个波长点的谱密度计算值进行了概率分布拟合、参数估计及拟合优度检验计算，其主要流程如下：

1)对轨道不平顺检测数据进行数据预处理及轨道不平顺谱计算；

2)提取不同波长下的谱密度样本，进行概率分布计算，剔除累积概率1%以下和99%以上的谱密度样本，以消除检测设备、线路结构异常的影响；

3)利用广义极值分布模型对青藏铁路不同波长谱密度值的分布概型进行拟合，采用极大似然估计法获取估计参数；

4)采用χ2拟合优度检验法对不同波长下的概率拟合函数进行假设检验，以验证谱密度样本服从广义极值分布。

3.2.2谱密度的概率分布拟合及其假设检验结果

经笔者统计分析，青藏铁路轨道不平顺不同波长的谱密度样本均可用广义极值分布函数表示，只是μ，σ和ξ等参数的估计值不同。限于篇幅，这里仅给出高低不平顺1.5，10和30 m波长的谱密度概率分布及其广义极值分布拟合函数。

(a)1.5 m波长谱密度的概率分布；(b)10 m波长谱密度的概率分布；(c)30 m波长谱密度的概率分布图1　不同波长的谱密度概率分布及其分布函数拟合Fig.1 Fitting of probability density function corresponding to spectrum densities of different wavelengths

从图1可知，采用广义极值函数能较好的拟合不同波长谱密度的概率分布。轨道高低和轨向不平顺不同波长谱密度的极值分布参数估计值见图2。

(a)形状参数；(b)尺度参数；(c)位置参数图2　轨道高低和轨向不平顺谱密度的广义极值分布参数估计值 Fig.2 Estimation values of GEV distribution of track profile vertical and alignment irregularities

从图2可知，不同波长谱密度广义极值分布的形状参数ξ>0，表明服从广义极值Ⅱ型分布(Frechet分布)。由此三参数(形状、尺度和位置参数)的估计值，可以根据式(3)反算不同波长在任意概率水平下的谱密度值。

采用χ2拟合优度检验法，根据式(8)计算的轨道高低、轨向、水平及轨距不平顺的X值见图3。

3.3轨道不平顺谱特征分析

百分位数谱实际上也是统计谱(与国内常用的平均值谱)等类同，从谱线可以发现其同样能表达周期性波长等特征，其在工程上意义较大，通过百分位能算出不同谱线的出现概率，此概率代表激振源的输入概率，以此算出的响应当然具有同样的概率，这对于系统可靠性的研究是重要的。

(a)轨道高低不平顺；(b)轨道轨向不平顺；(c)轨道水平不平顺；(d)轨道轨距不平顺图3　不同不平顺类型的X值Fig.3 Xvalues of different types of track irregularities

因此，为全面描述青藏铁路的线路几何状态及轨道不平顺谱线特征，图4～7给出了高低、方向、水平及轨距不平顺的10，30，50，70和90百分位谱及平均值谱，德国高、低干扰谱及美国五、六级谱的对比图。

由图4～7可知：

1)百分位谱同样能表达轨道不平顺的谱线特征。在轨检车有效检测波长范围内，不同类型的轨道不平顺平均谱基本处在70～80百分位谱之间。

2)轨道高低和轨向不平顺谱的倍频尖峰谱线较为明显，出现了3.14，3.59，4.18，4.97，6.21，8.32，12.49和24.98 m等周期性不平顺；而高低不平顺除这些特征波长外，在1～3 m波段也出现了较多周期性不平顺特征；轨道水平不平顺在2.88 m波长附近出现驼峰谱线，并且在24.98，12.34，8.32，6.20，4.97及4.14 m处也存在较微弱的凸型谱线。

图4　高低不平顺谱Fig.4 Track profile vertical irregularity spectrum

图6　轨向不平顺谱Fig.6 Track cross level irregularity spectrum

3)轨道高低和轨向不平顺谱曲线呈现复杂的窄带和周期波特征，尖峰谱线连续变化，含有与25 m轨长相关的周期性尖峰谱线；1～3.5 m周期性不平顺来源于钢轨轧制过程，与轧辊和校直辊直径误差、不圆度轧压力变化和轧制校直工艺水平等因素有关[24]，此波段不平顺会使簧下质量产生极大的冲击加速度。

图7　轨向不平顺谱Fig.7 Track gauge irregularity spectrum

4)轨道高低不平顺90百分位谱在2.55～7.01 m波段的不平顺状态处于德国高干扰谱与美国5级谱之间，状态较差；在11.13～37.93 m波段，不平顺状态与德国低干扰谱接近；在其他波段，轨道不平顺状态基本处于德国低干扰谱与美国六级谱之间。

5)轨道轨向不平顺在18.96 m波长以上的状态较好，基本与德国低干扰谱相当；除特征驼峰及尖峰谱线外，在18.96 m波长以下，轨道不平顺谱值基本处于德国低干扰谱与美国六级谱之间。

6)按照轨道不平顺谱值随波长的变化规律，根据图6的谱密度分布特征，水平不平顺有效波段取1～32 m是较为正确的。对于其90百分位谱，不平顺谱值在13.84～32 m波段与德国低干扰谱相当；而在13.84 m波长以下，不平顺状态处在德国高、低干扰谱之间。

7)轨距不平顺状态基本处于德国高干扰谱与美国六级谱之间，其90百分位谱也较微弱的反映了上述出现的连续尖峰谱线。轨距不平顺对于轮轨横向接触作用较为重要，而青藏铁路此项不平顺类型之状态有待进一步提高，应该作为重点关注的不平顺类型。

4　轨道不平顺谱拟合与百分位谱转换

4.1拟合公式及方法

为了全面表征青藏铁路的轨道不平顺谱线分布特征，笔者对国内外常见的轨道谱拟合公式进行了试算，认为中国干线铁路7参数公式的非线性拟合性能较优，其公式为

S=A(f2+Bf+C)/(f4+Df3+Ef2+Ff+G)

(9)

式中： f为空间频率，1/m；S为轨道不平顺功率谱值; A，B，C，D，E，F和G为拟合谱参数。

由于青藏铁路的轨道不平顺谱沿波长横轴方向分布极不规则，无显著的线性或分段线性特征，若对全波长谱线进行非线性拟合，将无法获得全局最优的拟合结果。

文献[16]采用分段拟合的方法实现了高速铁路轨道不平顺的幂函数拟合，本文借鉴这一方法。一般而言，对于轨道不平顺标准谱的制定，应该精细地考虑到不同波长谱密度的合理概率水平，故而本文对于轨道不平顺谱的拟合及概率处理方法如下：

1)计算获得青藏铁路轨道高低、方向、水平及轨距不平顺谱样本，以其统计平均值谱为拟合目标，并采用中值滤波方法进行消峰处理；

2)将有效截止波长分成三段(短波长段：1～2.5 m；中波长段：2.5～10 m；长波长段：10～70 m)，采用Levenberg-Marquardt非线性优化算进行7参数谱拟合；

3)根据公式(1)及其极大似然参数估计值，计算轨道不平顺统计平均值拟合谱密度值在其对应波长下的百分位(即累积概率水平)；

4)以轨道不平顺统计平均值拟合谱及其谱密度百分位分布为基础，计算平均值拟合谱密度与其它百分位谱密度之间的转换系数，通过公式(10)进行任意频率百分位谱的转换。

(10)

式中:CPL为累积概率水平；f为空间频率；SCPL(f)为百分位谱密度值；SM(f)为拟合谱密度值； KCPL.f、KM.f为对应百分位广义极值分布反函数值，可通过公式(3)进行计算。

4.2轨道不平顺谱顺拟合

图8～图11为采用铁科院7参数拟合公式以及分段拟合后的结果，有效波长范围1～70 m。

图中C.P.L(cumulative probability level)值为拟合谱密度对应的累积概率值(也即此谱密度值对应的百分位值)，由于篇幅所限，仅显示了部分谱密度对应的百分位值。从图8～11可知，采用7参数公式进行分段拟合的效果是较为可行的；在不同分段拟合谱的衔接处，存在较微小的谱值不平滑问题，但这对轨道不平顺的状态表达及随机反演影响极小，基本可以忽略。表2列出了青藏铁路轨道不平顺平均值谱在不同波段的参数拟合值。

图8　轨道高低不平顺谱拟合Fig.8 Fitting of track profile vertical irregularity

图10　轨道水平不平顺谱拟合Fig.10 Fitting of track cross-level irregularity

图11　轨道轨距不平顺谱拟合Fig.11 Fitting of track gauge irregularity

4.3平均值谱向百分位谱转换

根据广义极值分布理论，结合式(3)和式(10)，将不同不平顺类型的平均值拟合谱转换为10、70及90百分位数谱，并与实测谱进行比较；同时，文献[16]指出高速铁路轨道不平顺谱密度

表2　青藏铁路轨道不平顺平均值谱拟合参数

注：短波长段：1～2.5 m；中波长段：2.5～10 m；长波长段：10～70 m

基本服从自由度为2的χ2分布，故进一步与文献[16]的研究结果进行对比分析，见图12。

(a)高低不平顺百分位数谱;(b)方向不平顺90百分位谱;(c)水平不平顺90百分位谱;(d)轨距不平顺90百分位谱 图12　不同类型轨道不平顺10,70和90百分位转换谱与实测谱的比较Fig.12 Comparison of 90th transformed and measured spectrums of different types of track irregularities

实际上，在2.2.2节中笔者已经计算获得了不同轨道不平顺类型在不同波长下的谱密度广义极值分布参数估计值，可以根据式(3)反算不同波长在任意百分位下的谱密度估计值，限于篇幅，这里仅简单给出10，70及90百分位转换谱与实测谱的对比图。

由于国内外轨道不平顺标准谱均无法表达棍状尖峰或驼峰谱线特征，本文的统计平均值拟合谱线亦无法包含这些特征，这对于线路几何状态评价和动力学评估是不合理的。但是，本文在对不同波长谱密度样本进行广义极值分布参数估计时，已包含的周期性波长的尖峰谱线特征，从而可以根据需要在轨道不平顺平均值谱的基础上融合任意周期性波长在不同概率水平下的谱密度值，以实现更为合理的动力学激励输入要求。

5　结论

1)青藏铁路轨道高低和轨向不平顺谱曲线呈现复杂的窄带和周期波谱特征，在3.14,3.59,4.18,4.97,6.21,8.32,12.49和24.98 m等处连续出现倍频尖峰谱线，在1～3波段亦存在较多周期性成分，应该根据其原因改进施工及制造工艺，最大限度的消除周期性波长成分。

2)本文对中值滤波后的轨道不平顺平均值谱进行7参数拟合，获得了相应的特征参数，可以作为青藏铁路轨道不平顺的统计平均值谱，提供一个初步的线路状态评价标准谱。然而对于青藏铁路轨道不平顺标准谱的制定还需结合耦合动力学模型，进行轨道谱激励输入下的车辆、轨道系统动力响应评估，以获取最为经济、合理的统一标准谱。

3)可以采用广义极值分布进行青藏铁路轨道不平顺不同波长谱密度值的概率分布规律研究，本文通过极大似然估计法，获得了不同不平顺类型谱密度值的广义极值分布估计参数，可以反演有效波长下的任意百分位谱密度值，通过与标准谱线相融合，为线路几何状态评估、机车车辆设计及参数优化提供更为合理的激励输入。

[1]朱占元. 青藏铁路列车行驶多年冻土场地路基振动反应与振险预测[D]. 哈尔滨：哈尔滨工业大学，2009.

ZHU Zhanyuan. Train-induced vibration response and subsidence prediction of permafrost subgrade along Qinghai-Tibet railway[D]. Harbin: Harbin Institute of Technology, 2009

[2]陈士军. 青藏线含融化夹层和地下冰冻土路基列车行驶振动响应[D]. 哈尔滨：哈尔滨工业大学，2013.

CHEN Shijun. Train-induced vibration response of permafrost subgrade with ice layer and unfrozen interlayer along the Qinghai-Tiber railway [D]. Harbin: Harbin Institute of Technology, 2013.

[3]李涛. 青藏铁路多年冻土区路基的动力分析[J].铁道工程学报，2007，3(3)：29-32.

LI Tao. Dynamic analysis of subgrade structure of Qinghai-Tibet railway in permafrost region [J]. Journal of Railway Engineering Society, 2007, 3(3): 29-32.

[4]田立慧，凌贤长. 青藏铁路高温多年冻土区列车行驶路基长期永久变形数值模拟研究[J]. 地震工程学报，2014，36(4)：850-856.

TIAN Lihui, LING Xianzhang. Numerical simulation of permanent deformation of emban kment induced by train load in permafrost regions along the Qinghai-Tibet railway [J]. Journal of Earthquake Engineering, 2014, 36(4): 850-856.

[5]盛煜，温智. 青藏铁路多年冻土区热棒路基温度场三维非线性分析[J]. 铁道学报，2006, 28(1): 125-130.

SHENG Yu, WEN Zhi. Three-dimensional nonlinear analysis of thermal regime of the two-phase closed thermosyphon emban kment of Qinghai-Tibetan railway [J]. Journal of the China Railway Society, 2006, 28(1): 125-130.

[6]孙志忠，马巍，温智，等.青藏铁路多年冻土区普通路基地温监测及其预测分析[J].铁道学报，2010，32(3)：71-76.

SUN Zhizhong, MA Wei, WEN Zhi, et al. Experimental and numerical analyses on traditional emban kment of Qinghai-Tibet railway [J]. Journal of the China Railway Society, 2010, 32(3): 71-76.

[7]常利武，徐艳杰，乐金朝.动荷载作用下高温冻土路基动力响应的模拟实验研究[J].铁道学报，2011，33(11)：80-84.

CHANG Liwu, XU Yanjie, YUE Jinchao. Simulation experiment of dynamic response of high temperature frozen subgrade to dynamic loading [J]. Journal of the China Railway Society, 2011, 33(11): 80-84.

[8]翟婉明.车辆-轨道耦合动力学[M].北京：科学出版社，2014.

ZHAI Wanming. Vehicle and track coupling dynamics [M]. Beijing: Science Press,2007.

[9]佐藤吉彦.新轨道力学[M]. 徐涌等译.北京：中国铁道出版社，2001.

Misaki Sato Yoshihiko. New orbital mechanics [M]. XU Yong, Transl: et al. Beijing: China Railway Publishing House, 2001.

[10]陈宪麦，王澜，陶夏新，等.我国干线铁路通用轨道谱的研究[J].中国铁道科学，2008，29(3)：73-77.

CHEN Xianmai, WANG Lan, TAO Xiaxin, et al. Study on general track spectrum for chinese main railway lines [J]. China Railway Science, 2008, 29(3): 73-77.

[11]陈宪麦，王澜，陶夏新，等.我国干线铁路轨道平顺性评判方法的研究[J].中国铁道科学，2008，29(4)：21-27.

CHEN Xianmai, WANG Lan, TAO Xiaxin, et al. Study on the judgment method for track regularity of the main railway lines in China [J]. China Railway Science, 2008, 29(4): 21-27.

[12]练松良，刘洋，杨文忠. 沪宁线轨道不平顺谱分析[J]. 同济大学学报(自然科学版)，2007，35(10)：1342-1346.

LIAN Songliang, LIU Yang, YANG Wenzhong. Analysis of track irregularity spectrum of Shanghai-Nanjing railway [J]. Journal of Tongji University (Natural Science), 2007, 35(10): 1342-1346.

[13]练松良，李建斌，杨文忠. 沪昆线与金温线轨道不平顺谱分析[J]. 同济大学学报(自然科学版)，2010，38(2)：257-262.

LIAN Songliang, LI Jianbin, YANG Wenzhong. Analysis of track irregularity spectrum of Shanghai-Kunming and Jinhua-Wenzhou railways [J]. Journal of Tongji University (Natural Science), 2010, 38(2): 257-262.

[14]李再帏，练松良，李秋玲，等. 城市轨道交通轨道不平顺谱分析[J]. 华东交通大学学报，2011，28(5)：83-87.

LI Zaiwei, LIAN Songliang, LI Qiuling, et al. Characteristic analysis of track irregularity spectrum of urban rail transit [J]. Journal of East China Jiaotong University, 2011, 28(5): 83-87.

[15]徐磊，陈宪麦，李晓键，等. 朔黄重载铁路轨道不平顺谱分析[J]. 中南大学学报(自然科学版)，2013，44(12)：5147-5153.

XU Lei, CHEN Xianmai, LI Xiaojian, et al. Track irregularity spectrum analysis of Shenchi-Huanghua heavy haul railway [J]. Journal of Central South University (Science and Technology), 2013, 44(12): 5147-5153.

[16]康熊，刘秀波，李红艳，等. 高速铁路无砟轨道不平顺谱[J]. 中国科学：技术科学，2014，44(7)：687-696.

KANG Xiong, LIU Xiubo, LI Hongyan, et al. PSD of ballastless track irregularities of high-speed railway [J]. SCIENTIA SINICA Technologica, 2014, 44(7): 687-696.

[17]董连成，王定营，李广影，等. 青藏铁路轨道不平顺变化特征[J]. 沈阳建筑大学学报(自然科学版)，2013，29(6)：1013-1018.

DONG Liancheng, WANG Dingying, LI Guangying, et al. Research on the track irregularity variation characteristics of the Qinghai-Tibet railway [J]. Journal of Shenyang Jianzhu University (Natural Science), 2013, 29(6): 1013-1018.

[18]曾志平，余志武，张向民，等. 青藏铁路无缝线路试验段轨道不平顺功率谱分析[J]. 铁道科学与工程学报，2008，5(1)：37-40.

ZENG Zhiping, YU Zhiwu, ZHANG Xiang-min, et al. PSD analysis of track irregularity of continuously welded rail track in test zone of Qinghai-Tibet railway [J]. Journal of Railway Science and Engineering, 2008, 5(1): 37-40.

[19]Fisher R A, Tippett L H C. Limiting forms of the frequency distribution of the largest or smallest members of a sample [J]. Proc Cambridge Philos Soc, 1928, 24: 186-193.

[20]Kotz S, Nadarajah S. Extreme value distributions-theory and applications [M]. London Imperial College Press, 2000: 17-84.

[21]Coles S. An introduction to statistical modeling of extreme values [M]. New York: Springer Verlag, 2001: 36-78.

[22]杨谋存，聂宏. 三参数Weibull分布参数的极大似然估计数值解法[J]. 南京航空航天大学学报，2007，39(1)：22-25.

YANG Moucun, NIE Hong. Advanced algorithm for maximum likelihood estimation of three parameter weibull distribution [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(1): 22-25.

[23]王梓坤. 概率论基础及其应用(第三版)[M].北京师范大学出版社，2007：283-284.

WANG Zikun. The foundation of probability theory and its application (Third Edition) [M]. Beijing Normal University Press, 2007: 283-284.

[24]罗林，张格明，柴雪松，等. 轮轨系统轨道平顺状态的控制[M]. 中国铁道出版社，2006：208.

LUO Lin, ZHANG Geming, CAI Xuesong, et al. The control to the track irregularity state of wheel/rail system [M]. China Railway Publishing House, 2006: 208.

Research on track irregularity power spectrum density of Qinghai-Tibet railway

CHEN Xianmai1,2，XU Lei3，WANG Weidong1，HE Tianlong1，ZHANG Xiangmin1,2，XIANG Shang1，CHEN Wentao1

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;3. Track Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China)

Combining with relatively complete measured track irregularities on Qinghai-Tibet Railway, this paper systematically introduced probability theory into the study of track irregularity spectrum, and made an detail research on generalized extreme value distribution function fitting, parameter estimation and hypothesis testing for power spectrum density samples of different wavelengths. On this basis, the railway's track geometry status and characteristics of track irregularity spectrum were analyzed, and then formula fitting and parameter extraction were conducted for track irregularity statistical average spectrum using Levenberg-Marquardt algorithm and 7 parameters formula of Chinese trunk railways, last we proposed a method that any percentile spectrum could be transformed by track irregularity statistical average spectrum through which. The research results show that: the spectrum density values of different wavelengths obey the generalized extremum Ⅱ type distribution; the track profile vertical and alignment irregularity spectrum present complicated narrow-bands and periodic spectral lines, and its track gauge irregularity is mostly located in German high speed high disturbance line and American sixth grade track line; combined with the probability distribution laws of different wavelength spectrum densities, this paper suggests that we should consider and blend the peak spectrum line features on the basis of the statistical average spectrum for providing more reasonable dynamic simulation spectrum.

Qinghai-Tibet Railway; track irregularity power spectrum density; general extreme value distribution; parameter estimation; hypothesis testing; fitting

2015-11-25

国家自然科学基金资助项目(51478482)；中国铁路总公司科技研究开发计划课题资助项目(Z2013-G006)；铁道部科技研究开发计划课题资助项目(Z2012-066)

陈宪麦(1975-)，男，甘肃会宁人，副教授，博士，从事轨道动力学、线路状态评估及养护维修领域的研究； E-mail：xianmaichen@aliyun.com

U213.21

A

1672-7029(2016)09-1686-10