某轻型牵引炮方向机刚度特性对弹丸起始扰动的影响

张娅利,顾克秋,王　重

(南京理工大学 机械工程学院,南京 210094)



某轻型牵引炮方向机刚度特性对弹丸起始扰动的影响

张娅利,顾克秋,王重

(南京理工大学 机械工程学院,南京 210094)

为研究方向机刚度特性对弹丸起始扰动的影响,以某轻型牵引炮为例,建立了弹炮耦合全炮发射动力学有限元模型,分析了不同刚度下的弹丸起始扰动,在建立的弹丸起始扰动目标函数的基础上,研究了方向机刚度对弹丸起始扰动的影响规律。结果表明:随着方向机刚度的增大,弹丸起始扰动逐渐减小;该炮弹丸起始扰动随方向机刚度的变化呈现有利的变化趋势。

弹丸;方向机;刚度;弹炮耦合;起始扰动

火炮的射击精度一直是国内外众多火炮设计者所关心的问题,是火炮命中目标能力的度量。现有文献表明弹丸起始扰动对火炮射击精度有较为显著的影响。影响弹丸起始扰动的因素有很多,包括弹丸质量偏心、方向机刚度、高平机刚度、身管弹丸的接触特性等[1]。

关于弹丸起始扰动的影响因素,前人进行了大量研究。葛建立[2]利用Hypermesh软件分段扫描映射法,建立了某车载炮发射模型,考虑弹带变形,分析了身管自弯对弹丸起始扰动的影响;李强[3]建立了某牵引火炮弹炮耦合动力学有限元模型,分析研究了火炮相关参数对弹丸起始扰动的影响规律;张志军[4]通过建立某车载炮全炮弹炮耦合动力学有限元模型,分析了火炮座圈、高平机刚度特性对弹丸起始扰动的影响。

查看现有文献可知,火炮方向机刚度特性对弹丸起始扰动的影响研究有待进一步深入。方向机通过转动手轮带动回转部分转动完成方向瞄准。火炮发射时,在后坐力、动力偶矩和弹丸回转反作用力的作用下,回转部分会有绕自身转轴转动的趋势。对这种反传动如不加限制,瞄准位置就可能变位,直接影响弹丸起始扰动,而方向机对这种反传动的限制能力取决于其刚度特性。因此，研究方向机刚度特性对弹丸起始扰动的影响很有必要。本文以某牵引炮为例,建立弹炮耦合全炮发射动力学模型,就方向机刚度特性对弹丸起始扰动的影响展开计算研究,用弹丸起始扰动归一化函数值来评价弹丸起始扰动,该数值越小表明扰动情况越好,反之则越恶劣,因此利用该数值可以揭示方向机刚度对弹丸起始扰动的影响规律。

1　方向机刚度特性分析

方向机刚度特性可分为3个阶段:空回段、工作段和过载保护段。经过调炮过程,方向机空回量已经排完,因此本文主要研究在工作段方向机刚度特性对弹丸起始扰动的影响规律。方向机结构原理如图1所示。

图1　方向机结构原理图

1.1工作阶段刚度

由方向机结构原理图可知,工作阶段方向机刚度主要包括:轮齿啮合刚度,小齿轮轮体扭转刚度,轴扭转刚度,蜗轮轮体扭转刚度,蜗杆蜗轮轮齿啮合刚度以及蜗杆主体刚度。各部分刚度计算如下。

①齿轮轮齿啮合刚度。

使用石川公式计算两齿轮轮齿啮合刚度。石川公式是将齿轮轮齿简化为一个梯形和矩形组成的悬臂梁。关于这方面的文献资料有很多,具体的计算方法见文献[5]。

考虑到轮齿啮合是单齿、双齿交替啮合循环,通过数值计算,得到轮齿啮合的平均刚度K1。将蜗轮蜗杆啮合传动简化为齿轮齿条传动,同理可得蜗杆蜗轮轮齿啮合的平均刚度为K2。

②齿轮轮体扭转刚度。

齿轮轮体可看成由一个薄壁圆筒和一个连接输出轴的圆盘组成。因此齿轮轮体的扭转变形角度由以上两部分的扭转变形构成。薄壁圆筒是一种薄壁结构,可以应用弹性力学中的有关薄膜比拟理论知识求其扭转变形角度[6]:

(1)

式中:T为转矩;G为切变模量;r为筒体内壁的半径;d为壁厚;l为筒身长度。

圆盘的扭转变形角度:

(2)

式中:r2为圆盘外表面的半径;r1为圆盘内表面的半径;d1为圆盘的厚度。

轮体扭转刚度:

(3)

同理可得蜗轮轮体扭转刚度K4。

③蜗轮轴扭转刚度。

蜗轮轴为阶梯轴,对轴进行分段处理,计算其扭转变形量:

(4)

式中:Ti为蜗轮轴每段作用的转矩;li为蜗轮轴每段的轴长;Ip,i为蜗轮轴每段的极惯性矩[7]。

蜗轮轴所受转矩与扭转变形量的比值即为蜗轮轴扭转刚度K5。

④蜗杆轴向刚度。

蜗杆是压缩和弯曲的组合变形,对受载横截面而言,其轴向变形不是一个常值,因此,只能求得蜗杆轴向刚度的近似值K6。

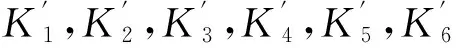
(5)

通过计算可得此阶段方向机系统回转刚度：

K=4.377 3×106N·m/rad

1.2过载保护阶段刚度

当传递到碟簧组上的力达到其预压载荷后,碟簧组开始受力变形,方向机进入过载保护阶段,这一阶段方向机的刚度还应考虑碟簧刚度。

按照GB/T1972-2005,碟簧载荷与变形关系式如下：

(6)

式中:F为碟簧所受载荷;E为碟簧材料的弹性模量;μ为碟簧材料的泊松比;ds为碟簧厚度;D为碟簧外圈直径;f为碟簧的变形量;h0为碟簧的自由锥高;k1,k4是根据碟簧的结构参数确定的计算系数,可查阅相关手册。参照此公式计算碟簧刚度。将碟簧组刚度统一到座圈轴向扭转刚度,按照1.1节中的计算方法可得此阶段方向机系统回转刚度:

K=6.212×105N·m/rad

将以上各阶段方向机受载变形曲线进行整合,即得方向机刚度特性曲线,如图2所示,用转矩Tr和回转角度δ的比值来表征方向机刚度。通过保持回转角度不变、改变转矩大小来改变方向机刚度。

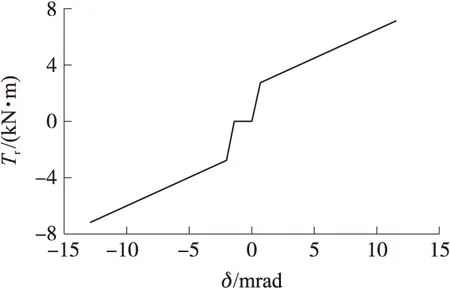
图2　方向机刚度特性曲线

本文拟采用表1中所述方案对弹丸起始扰动进行研究,表中,ηK为K的变化量。

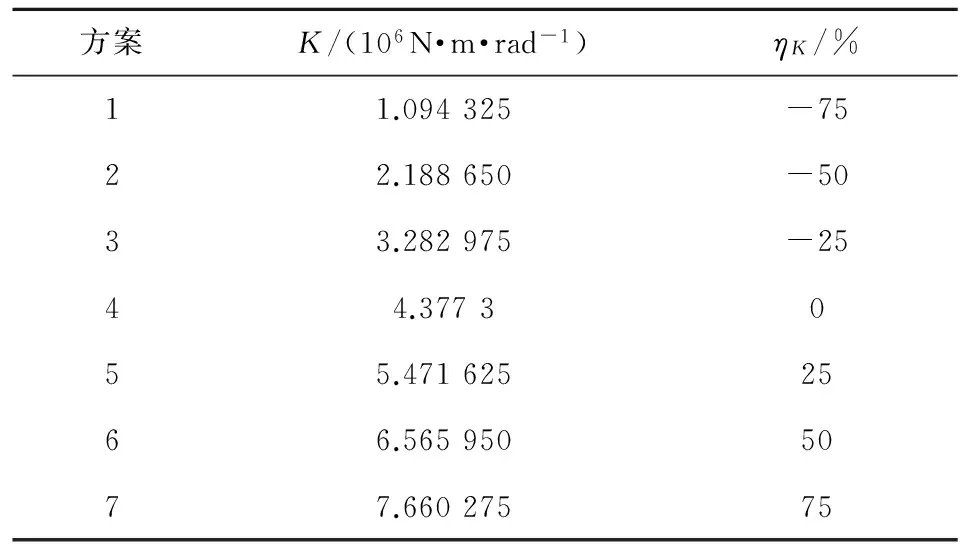
表1　分析方案

2　牵引炮弹炮耦合全炮发射有限元模型

2.1弹炮耦合基本假设

在火炮发射过程中弹丸与身管之间是多相作用,两者的作用机理十分复杂。基于建模技术和计算水平的考虑,本文在构建弹炮耦合全炮发射有限元模型时作出如下假设[2]:

①忽略挤进过程,初始状态弹带部分已完全挤入膛线,弹带不受挤进应力作用;

②忽略火药燃气高温对弹带的影响作用;

③不考虑火药后效作用和炮口制退器流场对弹丸运动的影响。

2.2弹炮耦合全炮发射模型

本文弹炮耦合全炮发射模型采用底凹式榴弹,炮体结构由下架、上架、摇架等组成。为了提高计算速度,牵引炮弹炮耦合有限元模型采用壳单元与实体单元混合建模,其中身管、炮口制退器、弹丸是实体单元,其他部件用壳单元。高平机利用单轴连接器模拟,对其施加高平机的初始平衡力和等效刚度;复进机与制退机也采用单轴连接器来模拟,并编写相关用户子程序。为了模拟方向机刚度特性对弹丸起始扰动的影响,且不增加计算量和时间,在火炮上架和下架之间建立连接器,连接器绕回转轴转动方向的刚度特性即为方向机刚度特性,将理论计算出的方向机刚度特性赋给连接器。本文模型选择在0°方向角、48°射角工况下进行分析,弹炮耦合全炮发射模型如图3所示。

图3　48°射角牵引炮弹炮耦合全炮发射动力学模型

3　方向机刚度特性对弹丸起始扰动的影响

3.1弹丸起始扰动目标函数

弹丸起始扰动由弹丸出炮口时刻的角位移、角速度与速度3个变量组成,该扰动对火炮的射击精度有重要影响。为了便于研究,对弹丸起始扰动3个变量进行加权处理,构建针对弹丸起始扰动的归一化函数[3]:

(7)

以身管轴线方向为x轴正向,垂直于x轴向上方向为y轴正向,由右手法则确定z轴正向,x轴和y轴确定的平面为竖直方向,x轴和z轴确定的平面为水平面。因此绕z轴旋转的角位移即为竖直方向角位移,绕z轴旋转的角速度即为竖直方向角速度,沿y轴方向的速度即为竖直方向速度;绕y轴旋转的角位移即为水平方向角位移,绕y轴旋转的角速度即为水平方向角速度,沿z轴方向的速度即为水平方向速度。式(7)中:θz,θy分别为出炮口时刻弹丸质心的竖直方向角位移和水平方向角位移;ωz,ωy分别为出炮口时刻弹丸质心的竖直方向角速度和水平方向角速度;vy,vz分别为出炮口时刻弹丸质心的竖直方向速度和水平方向速度;θz0,ωz0,θy0,ωy0,vy0,vz0为相应的弹丸起始扰动参考值;α1,β1,α2,β2,ζ1,ζ2为各弹丸参量的加权系数,其中α1,α2取0.3;β1,β2取0.15;ζ1,ζ2取0.05,是根据对弹丸起始扰动的影响程度来确定的经验值,满足α1+β1+ζ1+α2+β2+ζ2=1。

3.2刚度特性对弹丸起始扰动影响的分析

在建立的牵引炮弹炮耦合全炮发射动力学有限元模型的基础上,分析研究方向机刚度对弹丸起始扰动的影响。将计算的弹丸起始扰动参数列于表2。表2中不同方向机刚度下出炮口时刻各弹丸起始扰动参数的变化曲线如图4～图6所示,图中,λ为方向机刚度变化系数。

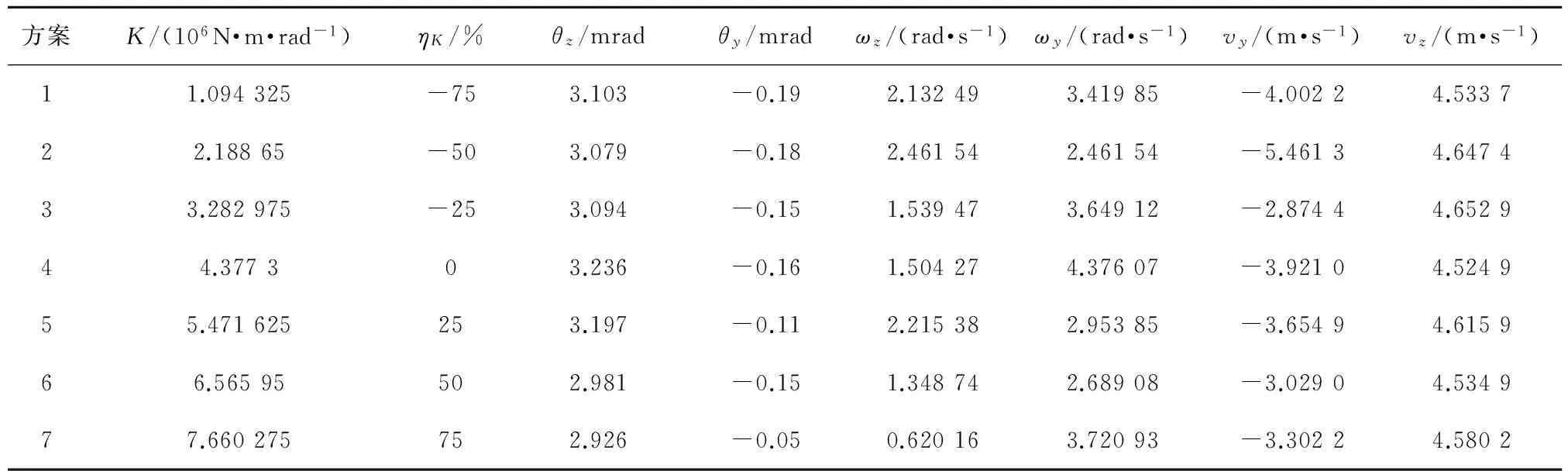
表2　弹丸起始扰动参数

图4　出炮口时刻角位移

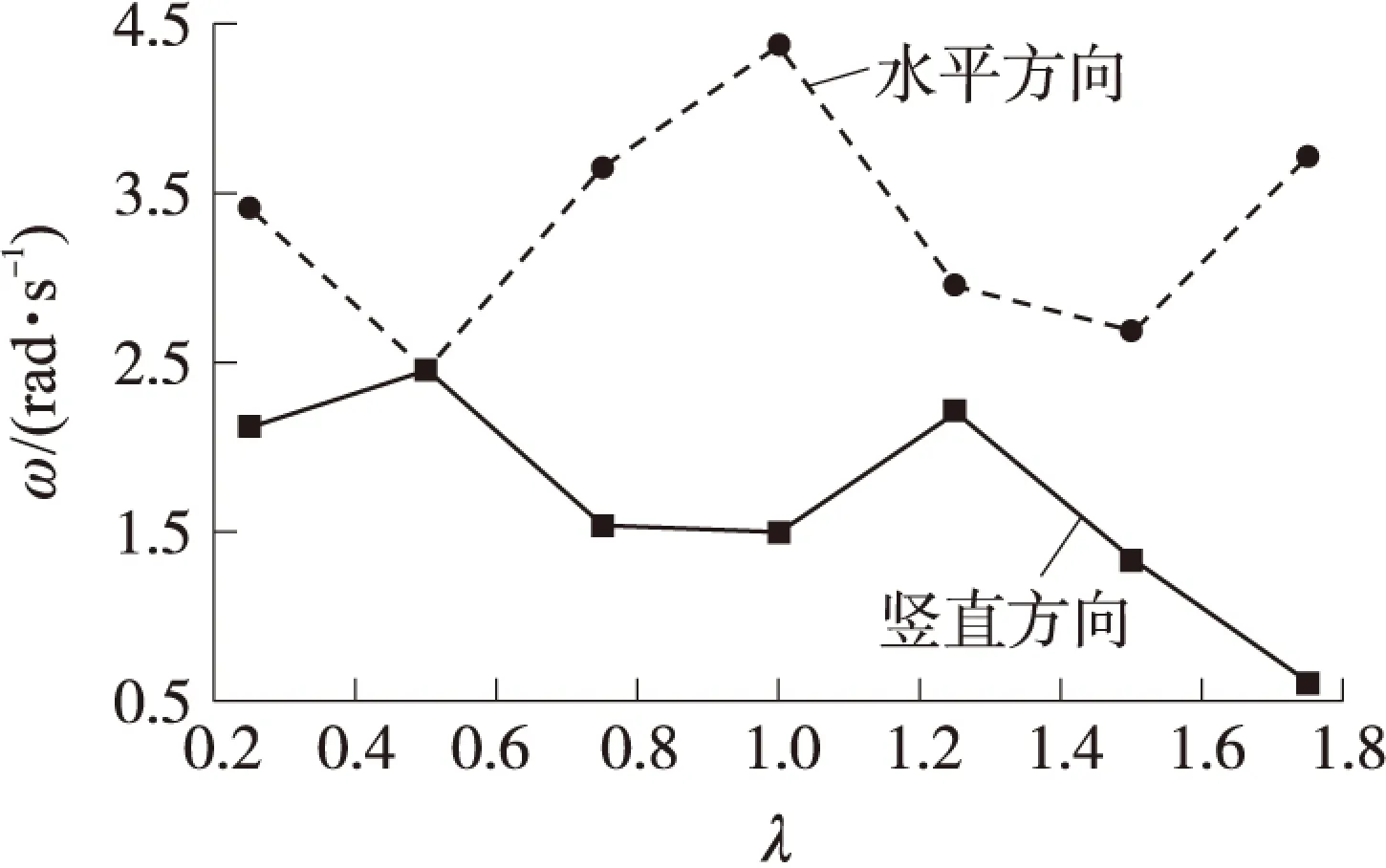
图5　出炮口时刻角速度

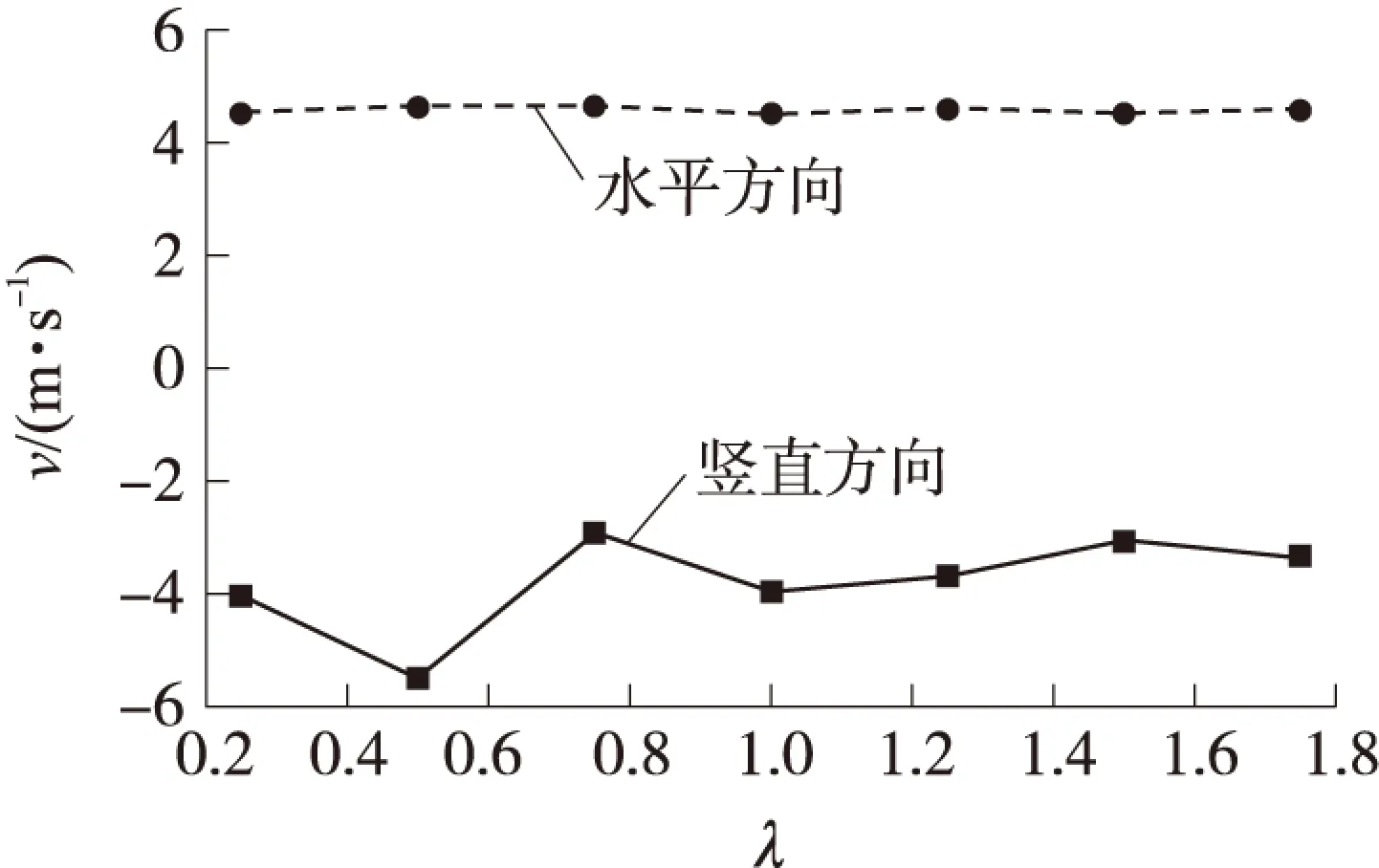
图6　出炮口时刻速度

由图4可知,随着方向机刚度的增大,出炮口时刻弹丸质心竖直方向角位移和水平方向角位移均有变化,虽变化幅度不大,但均呈现出逐渐减小的趋势。由图5可知,随着方向机刚度的增大,出炮口时刻弹丸质心竖直方向角速度和水平方向角速度均有明显波动,且变化幅度较大,其中竖直方向角速度整体上随方向机刚度的增大呈逐渐减小的趋势,而水平方向角速度无明显变化规律。由图6可知,随着方向机刚度的增大,出炮口时刻弹丸质心竖直方向速度存在明显变化,虽有数据跳动,但整体上仍然呈现出逐渐减小的趋势,而出炮口时刻弹丸质心水平方向速度随着方向机刚度的增大变化幅度较小,变化规律不明显。

选取表2中原方向机刚度、方向机刚度减小50%、方向机刚度增大50% 3种情况下的弹丸起始扰动参数并绘制部分膛内时期运动曲线,如图7～图10所示。

图7　竖直方向角位移

图8　水平方向角位移

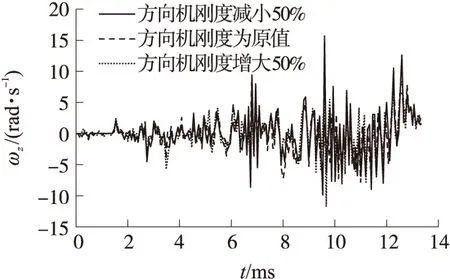
图9　竖直方向角速度

图10　水平方向角速度

由图7～图10可知,弹丸膛内运动过程十分复杂,原方向机刚度、方向机刚度减小50%、方向机刚度增大50% 3种情况下,方向机刚度变化对弹丸出炮口时刻附近的竖直方向角位移和水平方向角位移有一定影响;弹丸竖直方向与水平方向的角速度在出炮口时刻附近幅值有变化。

取K为原值时的各弹丸参量为弹丸起始扰动参考值,保持3.1中各弹丸参量的加权系数不变,将表2中所有方案的各弹丸参量分别代入式(7)得到各方案弹丸起始扰动归一化函数H值,如表3所示。

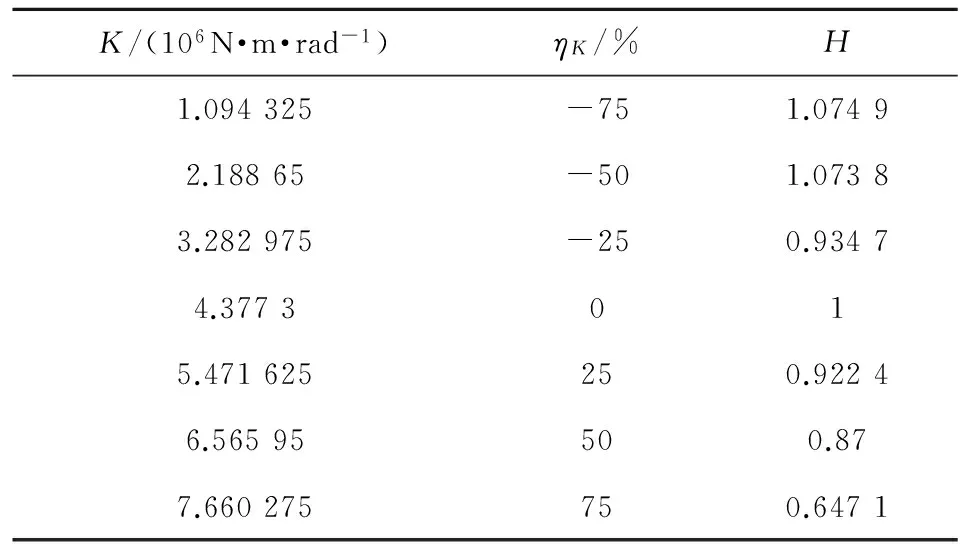
表3　目标函数

方向机不同刚度下目标函数H的变化曲线如图11所示。

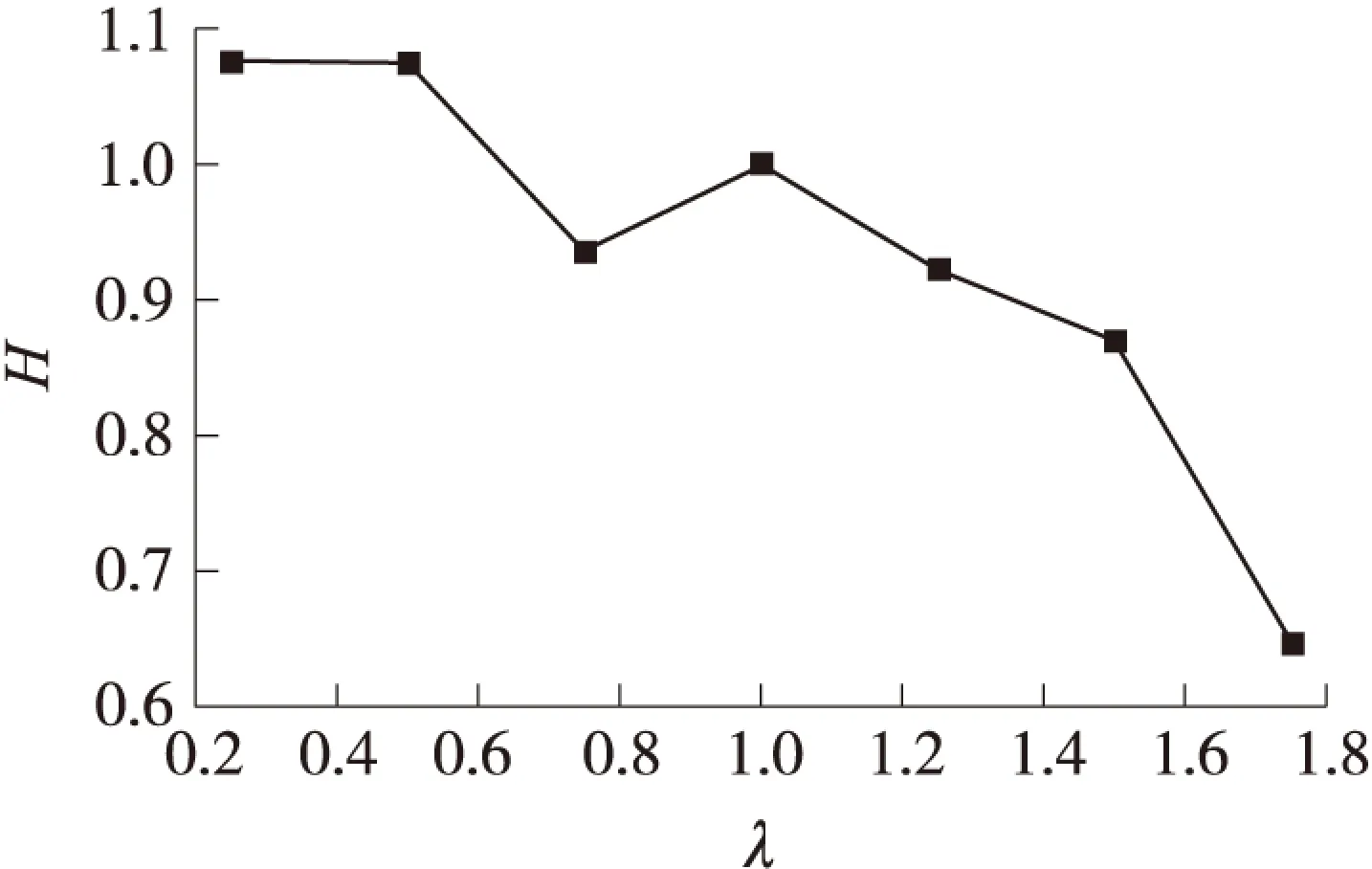
图11　方向机不同刚度下弹丸起始扰动变化曲线

由图11可知,本文所建立的牵引炮模型中方向机刚度与弹丸起始扰动之间呈现出非线性的关系。以方向机刚度原始值作为考核标准,随着方向机刚度的减小,弹丸起始扰动归一化函数H先减小且幅值小于1;而后增大,幅值大于1。这表明弹丸起始扰动随着方向机刚度的减小先改善而后变恶劣;随着方向机刚度的增加,弹丸起始扰动归一化函数H值逐渐减小且幅值小于1,表明弹丸起始扰动随着方向机刚度的增加得到改善。理论上,方向机刚度越大对火炮发射时回转部分反传动的限制能力越好,越有利于减小弹丸起始扰动,两者的结论相吻合。

样机试验表明,方向机刚度变化系数为1时,射击试验结果能够满足地面密集度指标,并且由于未考虑箱体、轴承等架体的变形,样机的方向机实际刚度要小于此理论值。由图11可知,随着方向机刚度变化系数从1大幅度减小,弹丸起始扰动归一化函数值总体上增大的幅度较小;随着方向机刚度变化系数从1增大,弹丸起始扰动归一化函数值减小明显。然而在实际情况下,提高方向机刚度存在一定难度。上述分析表明,该轻型火炮方向机刚度值在很大范围变化时对弹丸起始扰动无明显负面影响。

4　结论

本文通过建立某轻型牵引炮弹炮耦合全炮动力学模型,对不同方向机刚度下的弹丸起始扰动进行分析,研究了方向机刚度特性对弹丸起始扰动的影响规律。研究结果表明,随着方向机刚度的增大,弹丸起始扰动逐渐减小。获得的方向机刚度对弹丸起始扰动的影响规律能保证该火炮的射击密集度。本文方向机刚度分析方法具有普遍的参考价值。

[1]吴宏,赵有守.随机因素对弹丸起始扰动影响的分析方法[J].火炮发射与控制学报,2001(4):64-68.

WU Hong,ZHAO You-shou.A method to study random factor’s effections on initial disturbance of projectile[J].Journal of Gun Launch & Control,2001(4):64-68.(in Chinese)

[2]葛建立.车载炮动态非线性有限元仿真研究[D].南京:南京理工大学,2007.

GE Jian-li.Study on nonlinear dynamics simulation for vehicle-mounted howitzers by FEM[D].Nanjing:Nanjing University of Science and Technology,2007.(in Chinese)

[3]李强,顾克秋,王力.影响弹丸起始扰动的火炮结构参数灵敏度分析与优化研究[J].火炮发射与控制学报,2014(4):39-43.

LI Qiang,GU Ke-qiu,WANG Li.Sensitivity analysis and optimization of structure parameters for gun affecting initial projectile disturbance[J].Journal of Gun Launch & Control,2014(4):39-43.(in Chinese)

[4]张志军.大口径火炮关键连接部件特性研究[D].南京:南京理工大学,2016.

ZHANG Zhi-jun.Study on the character of critical connector components of large caliber gun[D].Nanjing:Nanjing University of Science and Technology,2016.(in Chinese)

[5]黄东升.复杂系统有限元建模技术及其在轻型火炮中的应用[D].南京:南京理工大学,2013.

HUANG Dong-sheng.Study on finite elements modeling technology of complex system and application in light artillery[D].Nanjing:Nanjing University of Science and Technology,2013.(in Chinese)

[6]郦黎伟,范元勋,罗明.谐波传动柔轮扭转刚度的研究[J].机械制造与自动化,2012,41(3):6-8.

LI Li-wei,FAN Yuan-xun,LUO Ming.Research on torsion stiffness of flexspline in harmonic gear[J].Machine Building & Automation,2012,41(3):6-8.(in Chinese)

[7]刘鸿文.材料力学Ⅰ[M].北京:高等教育出版社,2004.

LIU Hong-wen.Material mechanicsⅠ[M].Beijing:Higher Education Press,2004.(in Chinese)

Impact of Traversing Mechanism Stiffness of Light Towed Howitzer on Initial Projectile Disturbance

ZHANG Ya-li,GU Ke-qiu,WANG Zhong

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

To study the impact of traversing mechanism stiffness on the initial disturbance of projectile,a light towed howitzer was taken for example,and the finite element(FE)model of projectile-barrel coupling dynamics was established to analyze the initial projectile disturbance under different stiffnesses.Based on the established objective-function of initial disturbance of projectile,the rule of the traversing mechanism stiffness affecting the initial projectile disturbance was studied.The result shows that the initial projectile disturbance gradually decreases with the increase of the traversing mechanism stiffness.The change trend of the initial disturbance of the artillery projectile is beneficial with the change of the traversing mechanism stiffness.

projectile;traversing mechanism;stiffness;projectile-barrel coupling;initial disturbance

2016-05-18

武器装备重点预先研究项目

张娅利(1992- ),女,硕士研究生,研究方向为机械设计及理论。E-mail:327520569@qq.com。

顾克秋(1963- ),男,教授,研究方向为火炮系统轻量化技术、武器系统结构动力学与优化。E-mail:guyz101@njust.edu.cn。

TJ303.4

A

1004-499X(2016)03-0091-06