基于扩张状态观测器的攻击角度约束制导律

秦　潇,李　炯,邵　雷,董继鹏,张金鹏,3

(1.空军工程大学 防空反导学院,西安 710051;2.中国空空导弹研究院,河南 洛阳 471009;3.航空制导武器航空科技重点实验室,河南 洛阳 471009)



基于扩张状态观测器的攻击角度约束制导律

秦潇1,李炯1,邵雷1,董继鹏2,张金鹏2,3

(1.空军工程大学 防空反导学院,西安 710051;2.中国空空导弹研究院,河南 洛阳 471009;3.航空制导武器航空科技重点实验室,河南 洛阳 471009)

为满足现代战场对拦截弹特定攻击角度约束的要求,设计了一种自适应滑模制导律。以弹目视线角与视线角速率为状态变量,在二维平面建立了制导模型;采用一种自适应滑模趋近律,设计了具有攻击角约束的制导律;采用扩张状态观测器,对目标机动进行估计补偿,并用于所设计的制导律。进行了仿真分析,结果表明,所设计的制导律能够引导拦截弹以期望的角度命中目标,对于目标的机动具有一定的鲁棒性,能有效实现对目标实行特定角度攻击并基本满足零脱靶量的要求。

制导律;攻击角度约束;扩张状态观测器;机动补偿

制导律的选择决定了拦截弹以何种方式、按何种要求击中目标,因而不同的情况下需要选择不同的制导律。经过长期的发展，制导律的形式也变得更加多样化。传统意义的制导律设计的目的是在零脱靶量的前提下使拦截弹的过载尽量小,而在实际战场的很多情况下,还需要拦截弹以一定的攻击姿态命中目标。例如:希望反导拦截弹正面撞击目标以使得碰撞效果最强;希望反舰导弹从侧面垂直攻击舰船以最大杀伤目标等,这就对制导律的设计同时提出了零脱靶量和特定攻击角度的要求。传统的制导律显然忽略了特定攻击角度的约束要求,因此开展对这类制导律的研究很有必要。

文献[1]针对地面匀速目标,设计了一种以二次最优控制理论为基础的次优制导律。文献[2]对比例制导律进行了一些改进,通过增加一个时变偏置项,使得拦截弹具有一定的攻击角度,但其只能用于攻击非运动目标。文献[3]在分析了重力和拦截弹自动驾驶仪特性对制导系统的作用的前提下,在比例制导律上加上了一个偏置项,设计出了一种新型的比例制导律,仿真结果表明设计的制导律能在满足脱靶量要求的同时引导拦截弹以特定的攻击角度命中目标。文献[4]推导了制导过程中拦截弹视场角的解析式,并以剩余时间加权系数与初始制导条件为控制量,设计了一种具有攻击角度约束的最优制导策略。文献[5]对以偏置比例导引为基础的攻击角度约束制导律的攻击时间误差进行了分析,并在此基础上加入了一个附加项以控制攻击时间,最终设计了一种能够实现任意角度攻击的制导律,仿真结果证明了这种制导律的有限时间收敛性。文献[6]首次提出了一种时变的滑模面,满足零脱靶量与零攻击角度误差,并且在切换过程中满足拦截弹视场范围。同时用一种积分型障碍李雅普诺夫函数设计趋近律,设计了一种有限时间收敛的滑模制导律。

以上制导律对于拦截弹末端攻击角度的约束均具有一定的效果,然而对于由目标机动所引起的系统不确定性干扰却不能做到很好的处理。文献[7]采用了线性观测器的设计方法,将目标机动扩张为新的状态变量,并设计了状态观测器对其进行估计,仿真结果验证了该方法的收敛性与鲁棒性。

本文以特定攻击角度约束与零化视线角速率为目标,采用滑模控制理论设计了一种自适应滑模制导律。对于拦截弹导引头无法测量目标机动的问题,采用文献[7]的方法估计目标机动,并将其用于制导律的补偿。最后在MATLAB平台进行了仿真分析。仿真结果表明,所设计的制导律能实时跟踪目标机动,并使拦截弹能在以特定角度命中目标的同时获得较小的脱靶量,具有一定的工程意义。

1　平面制导模型的建立

图1表示拦截弹与目标在二维纵向平面的相对运动关系,T、M分别为目标与拦截弹;vt(t),vm(t)分别为目标与拦截弹的速度值,文中假设其大小保持不变;at(t),am(t)分别为目标与拦截弹的加速度值;θt(t)与θm(t)分别为目标与拦截弹的弹道倾角;q(t)为弹目视线角;R(t)为弹目相对距离。

图1　弹目二维平面相对运动图

根据参考文献[8]可得弹目相对运动学模型:

(1)

(2)

(3)

vmsin(q(t)-θm(t))

(4)

式(4)可化为

(5)

式(5)两边分别对t求微分,可得:

(6)

在此定义tf为制导终止时刻并定义如下2个状态变量:

(7)

(8)

(9)

w1(t)表示制导过程中拦截弹实际攻击角度与末端期望攻击角度之间的误差,w2(t)表示制导过程中弹目视线角速率。若能使制导过程中w2(t)趋向于零,则能保证制导终结时刻拦截弹的零脱靶量要求;而w1(t)趋向于零则能保证拦截弹命中目标时具有所期望的攻击角度。因此带末端攻击角度约束的制导律的设计的实质便是在给定期望攻击角度前提下控制拦截弹的弹道倾角,使得在制导终止时刻w2(t)和w1(t)能同时趋于零。

定义q*(tf)为制导终止时所期望的弹目视线角,由于在制导终止时刻可认为弹目视线角不再变化,故有:

(10)

(11)

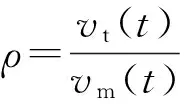
(12)

(13)

式(11)的意义在于在整个制导过程中,目标始终在拦截弹的探测视场范围内,即拦截弹能够捕获目标[9]。

因此,重新定义以下2个状态变量:

x1(t)=q(t)-q*(tf)

(14)

(15)

将带末端角度约束的制导律的设计转化为通过控制弹目视线角速率q(t)使得状态变量x1(t)与x2(t)在整个制导过程中趋于零。

对于式(14)与式(15),等式两边分别对t求微分,可得:

(16)

为便于计算,将式(16)中的相关变量进行重新定义,令

(17)

(18)

am,y(t)=am(t)cos(q(t)-θm(t))

(19)

at,y(t)=at(t)cos(q(t)-θt(t))

(20)

式(19)与式(20)中的am,y(t)与at,y(t)分别为拦截弹和目标在垂直于弹目视线方向上的机动加速度投影。

将式(17)～式(20)带入式(16),可化简得:

(21)

2　具有自适应特性的攻击角度约束制导律

针对上一节建立的制导模型,本节旨在对系统(21)设计相关的制导算法,以满足拦截弹在制导终段以所期望的攻击角度攻击目标,即满足在制导过程中状态变量x1(t)与x2(t)能向零趋近。

本节采用滑模变结构方法进行制导律的设计,为使x1(t)与x2(t)能趋近于零,选取滑模面如下:

(22)

式中:k1,k2为正常数。

为使系统(21)能以良好的动态特性到达滑模面,选择如下的自适应滑模趋近律:

(23)

式中:k3与ε为正常数。采用此滑模趋近律可以在弹目相对距离较大时适当放慢滑模趋近速率,使系统状态变量平稳地趋向期望值。当弹目相对距离逐渐减小到一定范围,趋近速率快速增大,系统状态变量迅速向滑模面收敛,确保拦截弹击中目标的同时具有一定的攻击角度。

将式(22)两边对t求微分,并结合式(2)、式(3)、式(23)可以求得具有自适应特性的满足攻击角度约束的制导律:

(24)

为证明本文所设计的制导律的稳定性,构建如下的Lyapunov函数:

(25)

对式(25)两边求微分可得:

(26)

将式(23)代入式(26)中可得:

(27)

3　针对目标机动估计的扩张状态观测器设计

针对第2节所设计的制导律(24)中存在的不确定性干扰at,y(t),本节旨在应用扩张状态观测器实现对目标机动的估计。

对于式(21)所建立的不确定性系统:

(28)

式中:-b2(t)am,y(t)为控制量,b2(t)at,y(t)为干扰量,y(t)为系统的输出值。

令x3(t)=-b2(t)at,y(t),并将x3(t)扩张为系统的状态,可建立新系统:

(29)

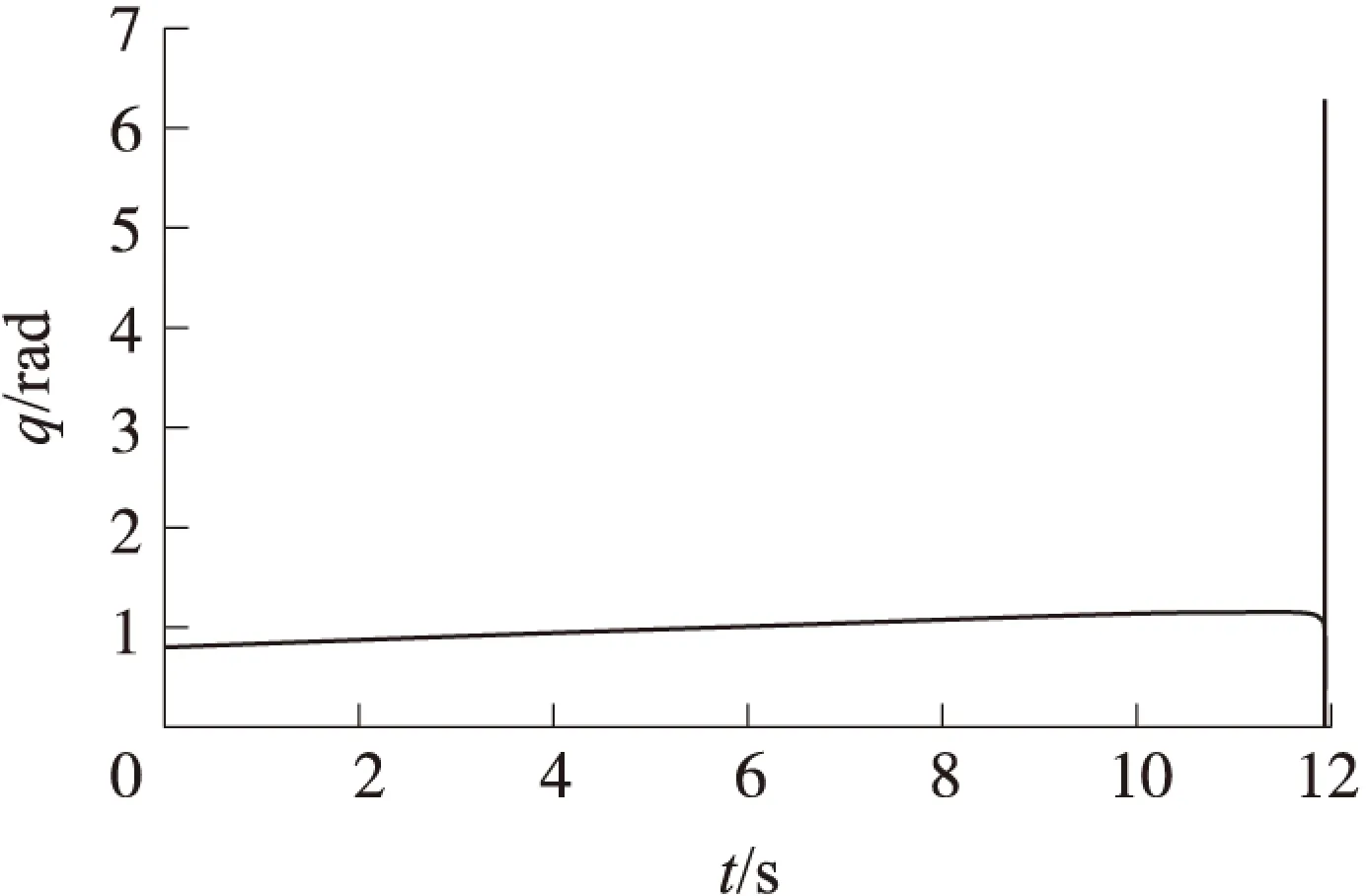
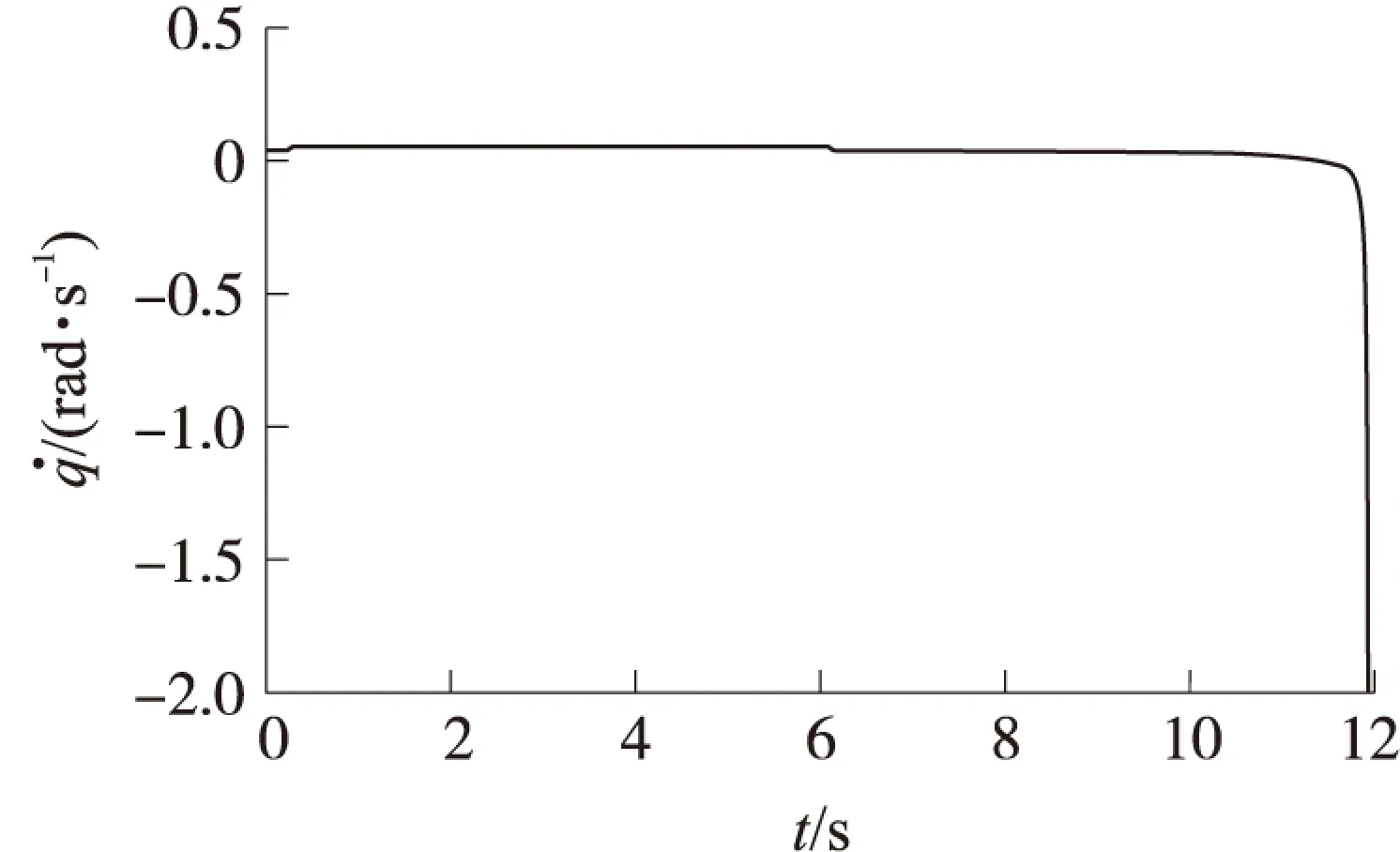
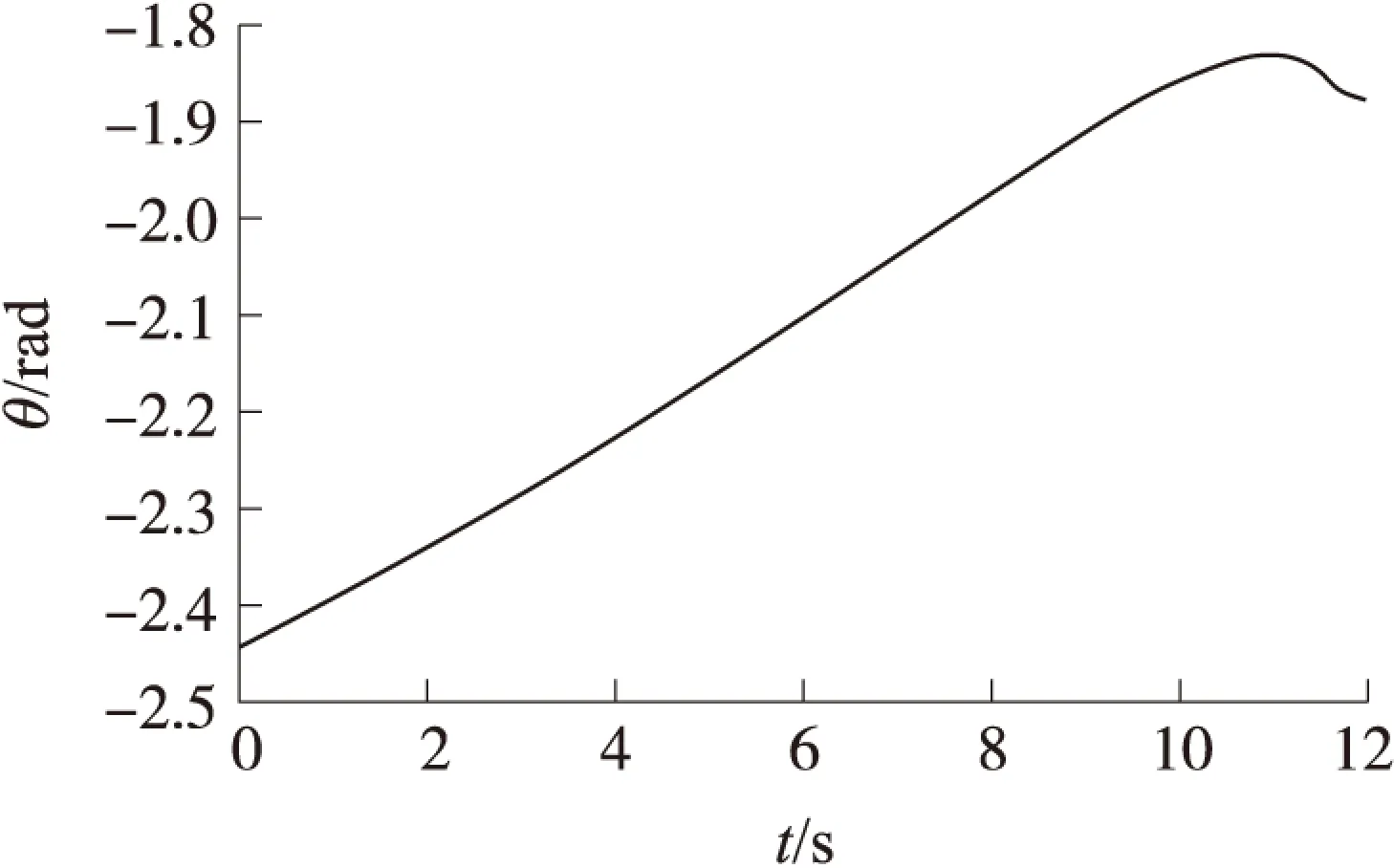
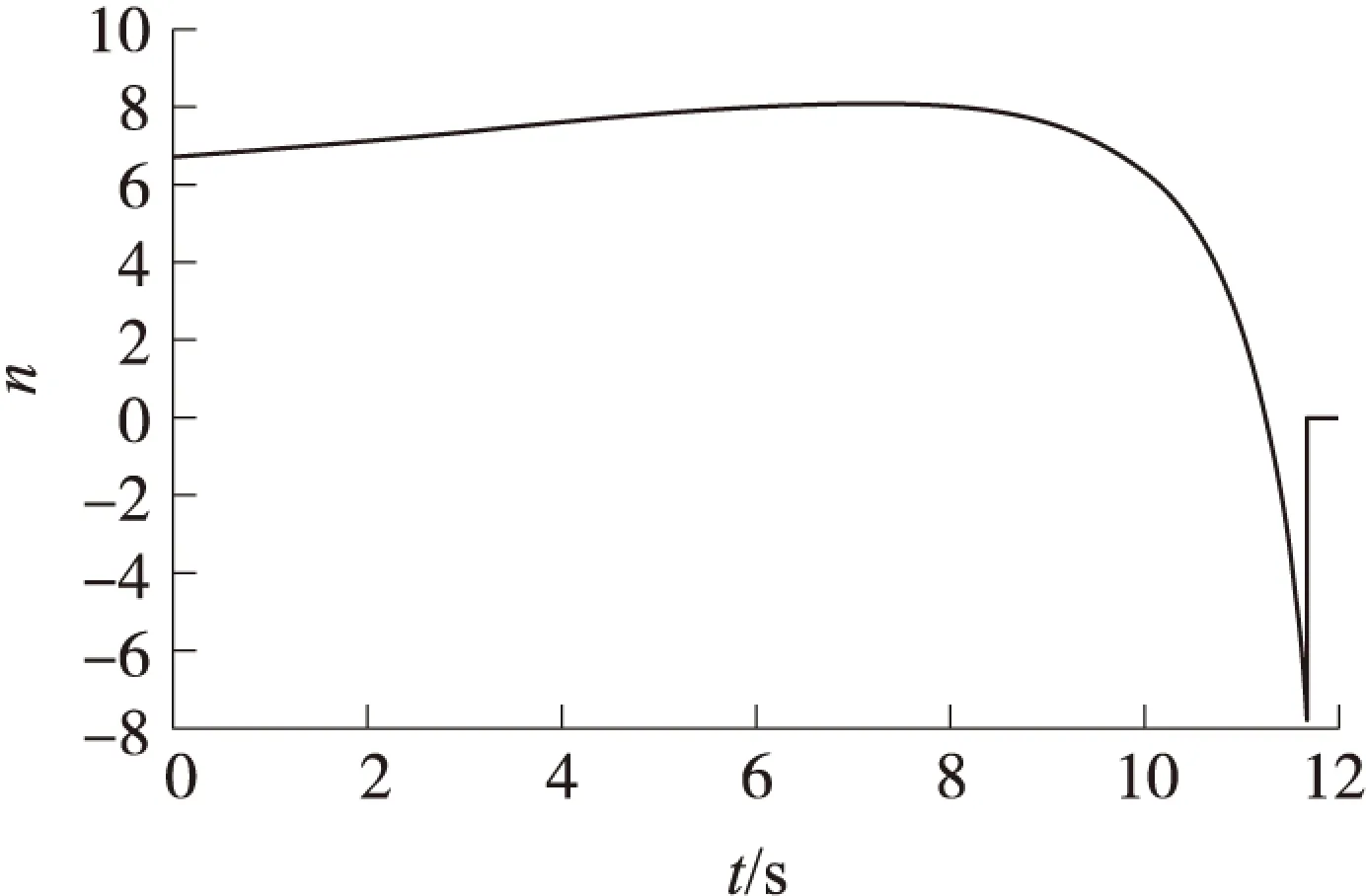
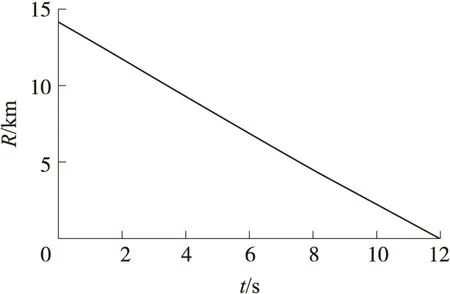
式(29)中,g(t)是干扰量x3(t)的导数,形式也是不确定的。当g(t)收敛于某一值,即|g(t)|

(31)

式中:0<α1<1,δ为常数。

4　仿真分析

图2为制导过程中拦截弹与目标的飞行轨迹,其大致反映了拦截弹垂直击中目标的整个过程。图3为扩张状态观测器的估计结果与目标机动垂直于弹目视线方向上的实际值的对比图,从图中可看出,本文所设计的扩张观测器能较好地跟踪被观测量。图4为扩张观测器的估计误差曲线,从中可以看出,估计误差值在较小的范围内波动,未出现较大的值,说明本文设计的扩张观测器具有良好的估计效果,基本满足制导律对目标机动补偿的需求。图5与图6分别为制导过程中的弹目视线角与弹目视线角速率的变化曲线,其值较为平稳地趋向某一值,证明了本文所设计制导律的稳定性。在最后一个时刻它们的值产生了一个小幅度的突变,这是由制导终结的那一刻弹目相对距离极小造成的,而这个时刻对制导效果的影响可以忽略不计。图7为拦截弹在飞行过程中攻击角度的变化曲线,反映了拦截弹的攻击角度向期望值收敛的过程。图8反映了制导过程中拦截弹过载的变化,从中可看出在制导过程中拦截弹的过载逐渐增大,到达峰值8左右后逐渐减小至零,而后反向增大至-8左右,之后迅速收敛至零,其峰值不超过8,这说明了本文设计的制导律的可行性。而在制导终止时刻拦截弹过载产生了一个突变,这是由于此时拦截弹已进入盲区,仿真中从此刻开始将拦截弹的过载置零所导致的。由于从盲区至制导终止时刻的时间极短,而在进入盲区之前拦截弹已具有了其所需的攻击角度,因而将拦截弹过载置零不会对制导效果造成影响,最终的仿真结果也证明了这一点。由图9可以看出,弹目相对距离随着时间的推进逐渐减小,并在制导终止时到达零附近,说明本文设计的制导律能大致满足零脱靶量的要求。

图2　弹目运动轨迹

图3　扩张观测器估计结果

图4　扩张观测器估计误差

为补偿仿真中可能出现的由各种因素引起的不确定性干扰,本文进行了200次蒙特卡洛仿真,对本文提出的制导律的脱靶量求取了平均值。最终求得其平均脱靶量为2.16 m,结果说明本文提出的制导律对于目标机动具有一定的鲁棒性,能基本满足拦截要求。

图5　弹目视线角

图6　弹目视线角速率

图7　拦截弹攻击角度

图8　拦截弹过载

图9　弹目相对距离

5　结论

本文以特定攻击角度约束与零化视线角速率为目标,采用滑模控制理论设计了一种自适应滑模制导律,同时利用扩张状态观测器估计目标机动,用于所设计的制导律中进行补偿。

仿真结果表明,在目标存在机动的情况下,该制导律能有效地实现对目标机动的补偿,达到对目标实行特定角度攻击的要求,并能基本满足零脱靶量的要求。

[1]KIM M,GRIDER K V.Terminal guidance for impact attitude angle constrained flight trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(6):852-859.

[2]KIM B S,LEE J G,HAN H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.

[3]KIM B S,LEE J.Homing guidance with terminal angular against non-maneuvering and maneuvering target,AIAA-97-3474[R].1997:189-199.

[4]WEN Qiu-qiu,XIA Qun-li,SU Wei-xia.A parameter design strategy for seeker’s field-of-view constraint in impact angle guidance[J].Journal of Aerospace Engineering,2015,229(13):2 389-2 396.

[5]ZHANG You-an,WANG Xing-liang,MA Guo-xin.Impact time control guidance law with large impact angle constraint[J].Journal of Aerospace Engineering,2015,229(11):2 119-2 131.

[6]WANG Xing-liang,ZHANG You-an,WU Hua-li.Sliding mode control based impact angle control guidance considering the seeker’s field-of-view constraint[J].ISA Transactions,2016,61:49-59.

[7]姚郁,王宇航.基于扩张状态观测器的机动目标加速度估计[J].系统工程与电子技术,2009,31(11):2 682-2 692.

YAO Yu,WANG Yu-hang.Acceleration estimation of maneuvering targets based on extended state observer[J].Systems Engineering and Electronics,2009,31(11):2 682-2 692.(in Chinese)

[8]雷虎民.导弹制导与控制原理[M].北京:国防工业出版社,2006.

LEI Hu-min.Theory of guidance and control for missile[M].Beijing:National Defense Industry Press,2006.(in Chinese)

[9]HA I J,HUR S J,KO S M.Performance analysis of PNG laws for randomly maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems,1990,26(5):713-721.

[10]王华吉.拦截高速机动目标的精确末制导方法研究[D].西安:空军工程大学,2014.

WANG Hua-ji.Study of accurate final guidance law for intercepting high maneuvering target[D].Xi’an:Air Force Engineering University,2014.(in Chinese)

Guidance Law with Terminal Attack Angle Constraint Based on Extended State Observer

QIN Xiao1,LI Jiong1,SHAO Lei1,DONG Ji-peng2,ZHANG Jin-peng2,3

(1.College of Air and Missile Defense,Air Force Engineering University,Xi’an 710051,China;2.China Airborne Missile Academy,Luoyang 471009,China;3.Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons,Luoyang 471009,China)

To meet the requirements of missile with terminal-attack-angle constraint in modern battlefield,an adaptive guidance law with terminal attack angle constraint was derived.A guidance model was deduced in the two-dimensional coordinate system by considering the LOS angles and its change rate as state variables.A guidance law with terminal-attack-angle constraint was designed by adopting an adaptive reaching law.An extended state observer was adopted to compensate the target maneuvering.The simulation results show that the guidance law can be used to hit the target with expected terminal-attack-angle.The guidance law has robustness for target maneuvering,and it meets the requirement of zero miss amount.

guidance law;attack angle constraint;extended state observer;maneuvering compensation

2016-05-04

国家自然科学基金项目(61573374;61503408);航空科学基金项目(20140196004)

秦潇(1992- ),男,硕士研究生,研究方向为空天拦截器制导、控制与仿真。E-mail:1299248660@qq.com。

李炯(1979- ),男,副教授,博士,硕士生导师,研究方向为空天拦截器制导、控制与仿真。E-mail:graceful001@126.com。

TJ765.3

A

1004-499X(2016)03-0053-06