库水-重力坝-无限地基系统地震响应分析*
2016-10-19刘钧玉张思淼王宇暘宁宝宽
刘钧玉, 张 萍, 张思淼, 王宇暘, 宁宝宽
(1. 沈阳工业大学 建筑与土木工程学院, 沈阳 110870; 2. 大连理工大学 水利工程学院, 辽宁 大连 116024; 3. 东北大学 资源与土木工程学院, 沈阳 110819)
库水-重力坝-无限地基系统地震响应分析*
刘钧玉1,2, 张萍1, 张思淼3, 王宇暘1, 宁宝宽1
(1. 沈阳工业大学 建筑与土木工程学院, 沈阳 110870; 2. 大连理工大学 水利工程学院, 辽宁 大连 116024; 3. 东北大学 资源与土木工程学院, 沈阳 110819)
为了分析库水以及无限地基辐射阻尼对库水-重力坝-无限地基系统的地震响应影响,通过比例边界有限元法、有限元法以及无限单元法计算了库水-重力坝-无限地基系统的响应.基于SBFEM计算上游坝面库水压力,利用无限单元法分析无限地基辐射阻尼的影响,以Koyna重力坝为研究对象,给出了重力坝在不同地基弹性模量条件下地震位移时程以及应力的响应,随着地基弹性模量的增加,坝体响应增加.与无质量地基模型的计算结果进行对比,考虑无限地基辐射阻尼的计算结果较小.
有限元分析; 比例边界有限元法; 重力坝; 库水压力; 无限单元; 动力相互作用; 无质量地基; 辐射阻尼
无限水域大坝与无限地基系统的动力相互作用对大坝的地震响应及大坝的抗震安全评价具有重要影响,因此受到很多研究人员重视.关于坝面动水压力的计算,目前计算动水压力的方法主要包括有限元法、边界元法及比例边界有限元法(scaled boundary finite element method,SBFEM)[1-3].有限元方法需要将无限水域截断为有限水域,一般库水范围在3~5倍坝高,这样较大范围的水域计算对有限元网格而言计算量比较大,并且有时无法严格满足远处的辐射边界条件即Sommerfeld辐射条件.边界元法也需要考虑一个较大的有限水域来近似无限水域,而且由于基本解的要求使得程序实现相对复杂.比例边界有限元法[4-6]集合了有限元方法和边界元方法的优点,首先,其严格满足无穷远处的Sommerfeld辐射条件,且不需要基本解;其次,它仅需要离散结构与地基交界面上的部分边界,从而降低了计算工作量.
本文应用SBFEM[7]计算库水-重力坝-无限地基系统中库水的动水压力,考虑了库水的可压缩性和库底岸坡边界的吸收作用,并通过无限单元法计算无限地基辐射阻尼的影响,针对库水-重力坝-无限地基系统进行分析,同时将计算结果与传统的无质量地基模型的计算结果进行对比,结果表明,考虑无限地基辐射阻尼影响的响应比无质量地基的响应要小.此外,随着地基弹性模量的增加,坝体的响应逐渐增大.
1 比例边界有限元计算动水压力基本方程
1.1动水压力控制方程
对于重力坝,假设库水是无粘性且小扰动理想液体,可压缩性库水在求解域内的控制方程为Helmholtz方程,即

(1)

(2)
库底和岸坡边界条件满足

(3)

(4)
其中,α为库底和岸坡的反射系数,当α=0时,表示不考虑边界吸收作用,即全反射情况,此时库底相当于刚性,完全没有淤沙的存在;当α=1时,代表库底和岸坡对动水压力波的完全吸收作用.库区表面边界条件(忽略库区表面微幅重力波)为
p=0
(5)
无穷远处边界条件为

(6)
式(6)采用标准的Sommerfeld边界条件,由于本文采用比例边界有限元方法,因此,无穷远处的边界条件是自动满足的.
1.2有限元方程及求解
1.2.1动水压力比例边界有限元方程
采用比例边界有限元方法对库水进行离散,由于库水可以理想化为沿着坝面上游方向延伸到无穷远处,因此,把比例边界有限元的相似中心O选在下游无穷远处,即可以不离散库水表面和库底.本文假定坝前水深恒定不变,从而可以使问题大为简化,离散的区域只有大坝迎水面,如图1所示.

图1 重力坝与库水离散示意图Fig.1 Schematic discrete for gravity dam and reservoir water
对式(1)~(3)使用加权余量方法可以得到关于动水压力的积分方程弱形式,即
(7)
式中:w为权函数;ΓS表示坝面;Γb为坝体与库底的交界线.在重力坝的情况下,二者分别退化为线和点.对式(7)进行分部积分,可以得到关于动水压力的频域控制方程及其坝面边界条件,即

(8)

B1=b1N
B2=b2N
式中:J为雅克比矩阵;η为SBFEM的轴向坐标;b1、b2为雅克比逆矩阵的第一列与第二列;N为型函数向量.
1.2.2有限元方程求解
为了求解已经建立的动水压力控制方程,引入新的变量,即

(9)
式中,

(10)
则式(9)可表示为

(11)
式中:

(12)

(13)
矩阵Z为Hamilton矩阵,其具有成对出现特征值的特性,使用特征值方法对式(11)进行求解,先求解Z的特征值问题,即
ZΦ=ΦA
(14)
则X的解为
X=ΦeλξConst
(15)
式中:λ为特征值矩阵;Φ为特征向量;A为特征向量的逆矩阵;Const为一组积分常数.从而可以得到控制方程的解,即

(16)
式中,F为余项矩阵,表达式见式(12).
在本文所研究的波传播问题中,对于由求解动水压力控制方程所引出的特征值则表示坝水系统的特征频率,且实部为正的特征值对应的特征向量代表波的传播模态,实部为负的特征值表示波的消散模态.当ξ→∞时,消散模态应为零,即水库上游无穷远处的动水压力应为零,此时,解的形式完成了对无穷远边界条件的自动满足.当ξ=0时,可以得到坝面上的动水压力X(ξ,ω)的两个分量,即
(17)
从而得到坝面动水压力,即

(18)
式中,T为余项矩阵,其表达式为

(19)
只有水平向地震激励时F=0,则有

(20)
由式(17)动水压力沿水库方向的衰减可得

(21)
由此可见,动水压力沿水库方向按指数规律衰减,坝面各点衰减规律相同,沿水库方向ξ等于常数的直立面上的动水压力分布规律相同.
2 无限地基模拟
关于无限地基的模拟,主要有全局法和局部法两种模拟方法,在工程应用中,一般采用无质量地基进行近似模拟无限地基.本文采用局部法中的无限单元法[8-10](infiniteelements)模拟无限地基的辐射边界条件.无限单元法的特点如下:
1) 通过位移插值函数使得在有限域与无限域交界面处的位移逐渐线性衰减到无穷远处为0的特点,从而考虑了无穷远处的边界条件;
2) 计算过程中能较好地吸收各种反射波,从而较好地模拟了半无限域地基的辐射阻尼效应,也就是考虑了结构-无限地基的动力相互作用;
3) 具有良好的稳定性,可用于长持时波动问题研究,因此,被嵌入到ABAQUS软件中模拟无限域的波动传播问题.

(22)
图2为入射波动时程图.弹性介质力学参数[11]为:弹性模量E=13.23GPa,泊松比ν=0.25,质量密度ρ=2 700kg/m3,横波cs=1 400m/s,纵波cp=2 425m/s,计算区域的范围为762m×381m,有限单元尺寸为19.05m×19.05m,时间步长取为0.005s.计算得到B(0,0),G(-19.05,0),H(19.05,0),E(0,-381),I(-19.05,-381),J(19.05,-381)等6个点的竖向位移时程,如图3所示.从底部E、I、J三个点的位移时程可以看出其竖向位移值基本相同.从顶部B、G、H三个点的竖向位移时程以及位置可以看出,B、G、H三点的位移值相同,说明是由入射波和反射波共同引起的位移时程,且顶部竖向位移的最大值为接近入射波幅值的2倍,如图4b是图4a的2倍.
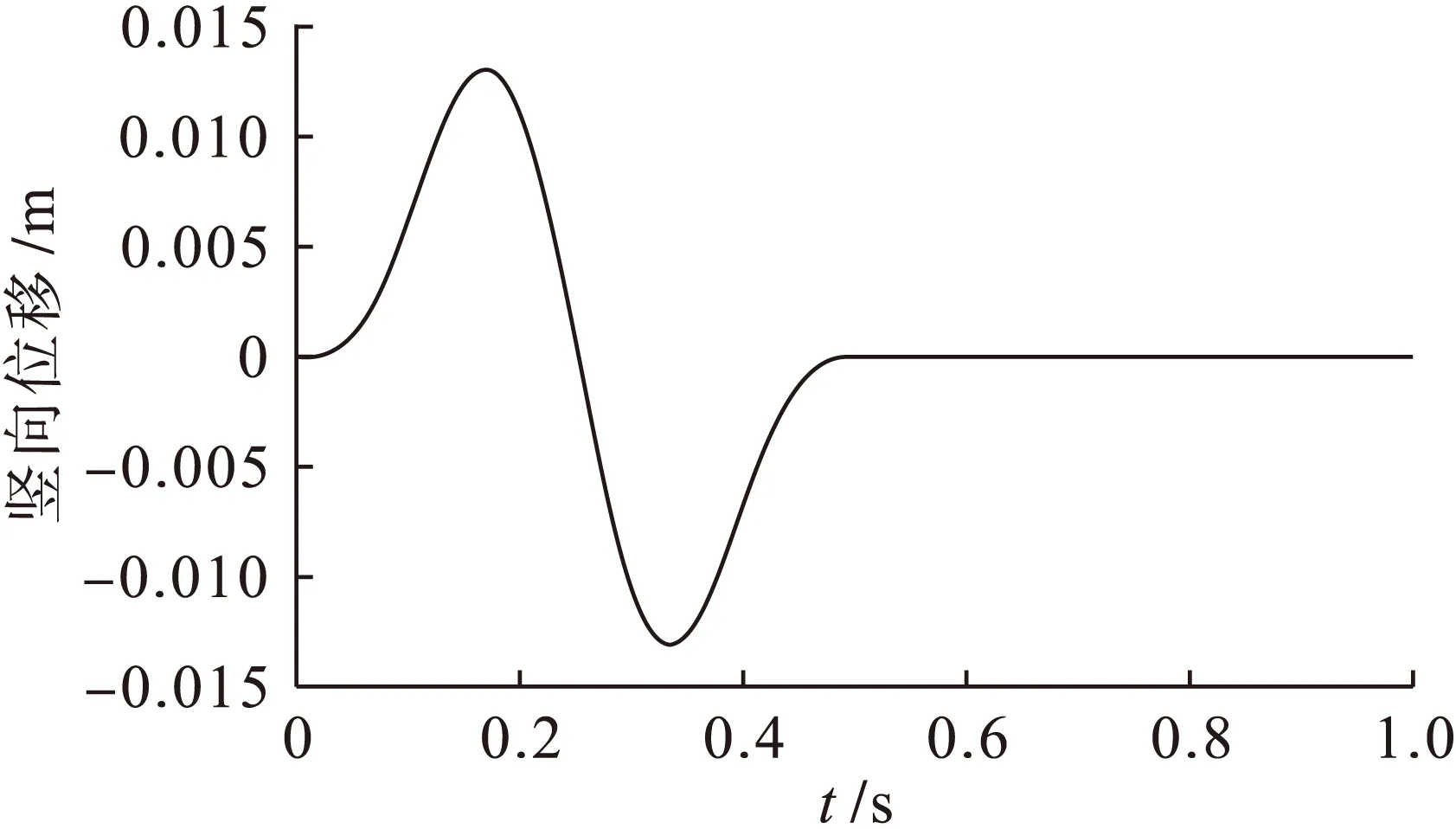
图2 入射波动时程图Fig.2 Time history of input wave

图3 有限元-无限元网格图Fig.3 Finite element-infinite element mesh
3 库水-坝体-地基系统模拟
3.1均匀无限地基模型
本文以Koyna坝为例,采用无限单元法与无质量地基模型模拟无限地基.重力坝的坝高103m,底部宽70m,上游坝面垂直于地基,地震时库水深90m,网格中包含了760个4节点平面应变单元,每层20个单元,最大单元尺寸为2.708m,最小单元尺寸为2.083m,弹性模量E=3.102 7GPa,泊松比ν=0.15,质量密度ρ=2 643kg/m3.地基的上下游范围分别取坝高的1、1.05、1.2、1.5、1.7倍5种情况,网格中包含了836个4节点平面应变单元和64个4节点平面应变无限单元,最大有限元单元尺寸为7.30m,最小有限元单元尺寸为2.354m,最大无限元单元尺寸为14.59m,最小无限元单元尺寸为10.00m,弹性模量E=7.3GPa,泊松比ν=0.3,质量密度ρ=2 842kg/m3,地基与基础之间使用了过渡网格的形式,最后将无质量的有限元地基(见图5a)分别与1、1.05、1.2、1.5、1.7倍无限元地基(见图5b)进行了比较.
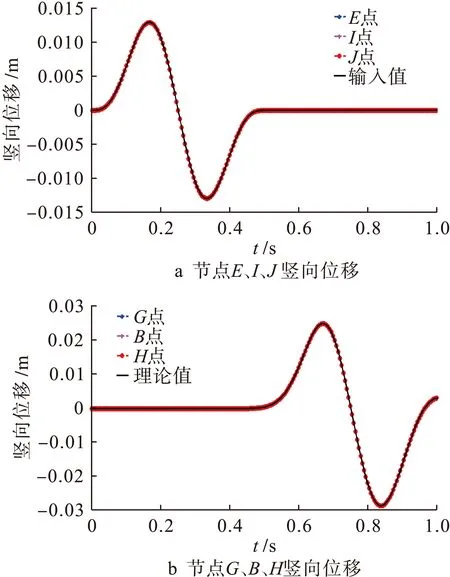
图4 P波垂直入射时各点竖向位移时程Fig.4 Time history of vertical displacement for variouspoints under normal incidence of P wave

图5 重力坝与两种地基网格离散图Fig.5 Discrete of gravity dam andmesh of two foundations
计算中输入顺河向Koyna地震波,其加速度峰值为0.3 g,大坝-地基混凝土阻尼比选为5%,总计算时间为29.98s.库水水位按照90m水深计算,计算结果如表1、2所示.

表1 作用在两种地基上的坝体最大应力
注:St表示最大拉应力,Sc表示最大压应力.
由表1、2对比可知,无质量地基模型的位移及拉压应力的响应均比无限地基(即1.7倍无限地基)模型的响应要大.

表2 作用在两种地基上的坝体最大位移
注:Umax表示正向最大位移,Umin表示负向最大位移.
3.2不同弹性模量情况下无限地基
为了比较不同地基弹模对辐射阻尼的影响,引入系数U,U=Ed/Ef,其中,Ed是重力坝的弹性模量,Ef是地基的弹性模量,取U分别为0.25、0.5、1.0、1.5、2.0、4.0、8.0这7种情况,将其中6种情况分别与U=1这一情况进行比较,计算结果如表3、4和图6所示.

表3 不同地基弹性模量情况下坝体最大应力

表4 不同地基弹性模量情况下坝体最大位移
由图6和表3、4可以看出,无限地基模型地基弹模的不同,对于重力坝的动力响应有着显著差别,坝体弹模不变,U变大,地基弹模越小,表明地基越柔软,但是在U=2时,应力与位移均达到最大,在0.25~2之间,拉压应力均成递增趋势,位移变化也逐渐增大;在2~8之间,位移与应力响应呈逐渐递减趋势.这是因为地基的柔度过大,已经达到极限,这时整体大坝的动力响应增大,因此,地基弹模是决定地基辐射阻尼影响大坝响应的重要因素,弹模越小,地基刚度越小,地基辐射阻尼效应越显著.

图6 不同弹性模量情况下水平位移变形曲线图Fig.6 Curves for horizontal displacement deformationunder different elastic modulus conditions
4 结 论
本文通过比例边界有限元方法、有限元法以及无限单元法计算了库水-重力坝-无限地基系统的响应,基于比例边界有限元SBFEM方法计算上游坝面库水压力,基于无限单元法考虑无限地基辐射阻尼的影响.以Koyna重力坝为研究对象,给出了重力坝的地震位移时程以及应力的响应,并与工程中常用的无质量地基模型的计算结果进行对比,结果表明,考虑辐射阻尼的无限地基计算得出的结果比无质量地基模型计算得出的结果小.通过对重力坝在无质量地基模型与无限地基模型的对比、不同弹性模量情况下的对比得出以下结论:
1)SBFEM方法可以方便有效地计算无限水域与坝体的相互作用问题;
2) 基于无限元考虑辐射阻尼的无限地基相对于无质量截断的有限元地基而言,应力与位移都有一定的降低;
3) 在不同的地基弹性模量情况下,随着地基弹性模量的增加,坝体响应增加.
[1]王毅,林皋,胡志强.考虑库水特性的重力坝动水压力求解 [J].沈阳工业大学学报,2014,36(1):114-120.
(WANGYi,LINGao,HUZhi-qiang.Solutionofhydrodynamicpressureongravitydamwithconsideringcharacteristicsofimpoundedwater[J].JournalofShenyangUniversityofTechnology,2014,36(1):114-120.)
[2]LinG,WangY,HuZQ.Anefficientapproachforfrequency-domainandtime-domainhydrodynamicanalysisofdam-reservoirsystems[J].EarthquakeEngineering&StructuralDynamics,2012,41(13):1725-1749.
[3]林皋,杜建国.基于SBFEM的坝-库水相互作用分析 [J].大连理工大学学报,2005,45(5):723-729.
(LINGao,DUJian-guo.Analysisofdam-reservoirinteractionbasedonSBFEM[J].JournalofDalianUniversityofTechnology,2005,45(5):723-729.)
[4]王毅,胡志强.基于比例边界有限元的拱坝动水压力计算 [J].水电能源科学,2011,29(2):44-46.
(WANGYi,HUZhi-qiang.Dynamicwaterpressurecalculationofarchdambasedonfiniteelementme-thod[J].WaterResourcesandPower,2011,29(2):44-46.)
[5]陈灯红,杜成斌.结构-地基动力相互作用的时域模型 [J].岩土力学,2014,35(4):1164-1172.
(CHENDeng-hong,DUCheng-bin.Timedomainmodelofstructure-foundationdynamicinteraction[J].RockandSoilMechanics,2014,35(4):1164-1172.)
[6]SongCM.Thescaledboundaryfiniteelementmethodinstructuraldynamics[J].InternationalJournalforNumericalMethodsinEngineering,2009,77(8):1139-1171.
[7]LuS,LiuJ,LinG.Highperformanceofthescaledboundaryfiniteelementmethodappliedtotheinclinedsoilfieldintimedomain[J].EngineeringAnalysiswithBoundaryElements,2015,56:1-19.
[8]戚玉亮,大塚久哲.ABAQUS动力无限元人工边界研究 [J].岩土力学,2014,35(10):3007-3012.
(QIYu-liang,HISANORIOtsuka.StudyofABAQUSdynamicinfiniteelementartificialboundary[J].RockandSoilMechanics,2014,35(10):3007-3012.)
[9]ZhaoC.Computationalsimulationofwavepropagationproblemsininfinitedomains[J].ScienceChina(Physics,Mechanics&Astronomy),2010,53(8):1397-1407.
[10]HoumatA.Acoupledfinite-hierarchicinfiniteelementmethodforaninhomogeneoustransverselyisotropicsoillayerunderirregularlydistributedstripload[J].AppliedMathematicalModelling,2015,39(12):3341-3356.
[11]王晓亮.混凝土坝地震响应特性研究 [D].宜昌:三峡大学,2010.
(WANGXiao-liang.Studyonseismicresponseofconcretedams[D].Yichang:ChinaThreeGorgesUniversity,2010.)
(责任编辑:钟媛英文审校:尹淑英)
Seismic response analysis for reservoir water-gravity dam-infinite foundation system
LIU Jun-yu1, 2, ZHANG Ping1, ZHANG Si-miao3, WANG Yu-yang1, NING Bao-kuan1
(1. School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China; 2. School of Hydraulic Engineering, Dalian University of Technology, Dalian 116024, China; 3. School of Resource & Civil Engineering, Northeastern University, Shenyang 110819, China)
In order to analyze the effect of reservoir water and infinite foundation radiation damping on the seismic response of reservoir water-gravity dam-infinite foundation system, the response of reservoir-gravity dam-infinite foundation system was calculated with the scaled boundary finite element method (SBFEM), finite element method (FEM) and infinite element method. The reservoir water pressure at the upstream surface of gravity dam was calculated based on SBFEM, and the effect of the infinite foundation radiation damping was analyzed with the infinite element method. Through taking Koyna gravity dam as the research subject, the response of seismic displacement time history and stress of gravity dam under the condition of different elastic modulus of foundation was obtained. With increasing the elastic modulus of foundation, the dam response increases. Compared with the calculated results from the massless foundation model, it is found that the calculated results with considering the effect of infinite foundation radiation damping are smaller.
finite element analysis; scaled boundary finite element method; gravity dam; reservoir water pressure; infinite element; dynamic interaction; massless foundation; radiation damping
2015-11-02.
国家自然科学青年基金资助项目(51109134/E090801,51208310,51408585); 中国博士后基金资助项目(2013T60283).
刘钧玉(1978-),男,辽宁沈阳人,副教授,博士,主要从事断裂力学数值方法和结构地基相互作用等方面的研究.
10.7688/j.issn.1000-1646.2016.05.16
TU 398
A
1000-1646(2016)05-0566-07
*本文已于2016-05-12 13∶56在中国知网优先数字出版. 网络出版地址:http:∥www.cnki.net/kcms/detail/21.1189.T.20160512.1356.016.html
