基于三参数双τ2强度理论的厚壁圆筒极限压力分析*
2016-10-19陈四利李艳宇张精禹
陈四利, 李艳宇, 张精禹
(沈阳工业大学 建筑与土木工程学院, 沈阳 110870)
基于三参数双τ2强度理论的厚壁圆筒极限压力分析*
陈四利, 李艳宇, 张精禹
(沈阳工业大学 建筑与土木工程学院, 沈阳 110870)
为了得到均布载荷作用下拉压同性材料与拉压异性材料厚壁圆筒弹塑性分析全过程的统一解析解,采用三参数双τ2强度理论对厚壁圆筒进行弹塑性应力分析.通过引用三参数双τ2强度理论中的极限应力比α与β对拉压同性材料和拉压异性材料进行了统一分析,分别得到了弹性极限压力、弹塑性极限压力以及弹塑性区应力与材料的极限应力比和弹塑性半径的关系式.结果表明,不仅材料的极限应力σt、极限应力比α和β对厚壁圆筒的极限承载能力有影响,而且厚壁圆筒的内、外半径亦与厚壁圆筒的极限压力有关.
均布载荷; 解析解; 厚壁圆筒; 极限应力比; 弹塑性应力; 弹性极限压力; 弹塑性极限压力
Tresca强度理论和Mises屈服准则只适用于拉压同性材料,而在实际工程中,大部分材料均属于拉压异性材料,因此,采用Tresca强度理论和Mises屈服准则对这类材料进行弹塑性分析将产生较大误差.近年来,对于拉压异性材料厚壁圆筒或厚壁圆环的弹塑性分析引起众多学者的广泛关注,并且取得了良好的进展[1-5].1990年统一强度理论提出之后,杨宇宙[6-7]、敖文刚[8]均采用双剪统一理论进行了厚壁圆筒极限载荷统一解的分析,不同之处在于其充分考虑了中间主应力σ2对材料的影响.本文采用三参数双τ2强度理论对厚壁圆筒进行极限压力分析,在考虑中间主应力对材料的影响以及材料极限拉压比不同的基础上,充分思量了不同材料的剪拉比不同的特点,使其更好地适用于不同材料的极限应力分析.
1 三参数双τ2强度理论

(1)

假设3种极限应力状态分别为单轴拉伸应力状态、单轴压缩应力状态以及纯剪切应力状态.设单轴压缩极限应力为σc,单轴拉伸极限应力为σt,剪切极限应力为τk,将3种极限应力表示3个主应力,并引入极限应力比α和β,其中,α=σc/σt,β=τk/σt,分别代入式(1)可求得3个参数的表达式,即
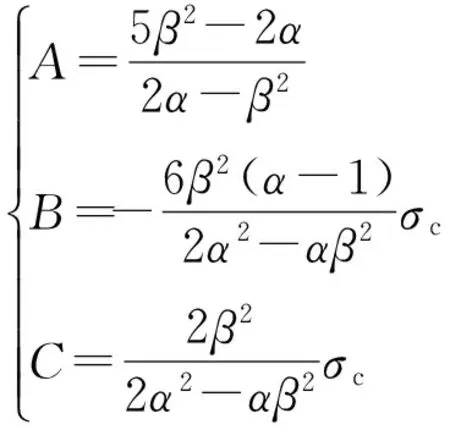
(2)
将式(2)及主剪应力和平均应力表达式代入式(1),可得新的三参数双τ2强度理论表达式,即
(3)
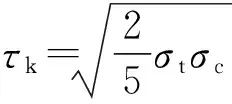
2 厚壁圆筒的极限压力分析
图1为厚壁圆筒模型.某受均布荷载作用下的厚壁圆筒,外半径为rm,内半径为rn,其受均布荷载为q,假设材料为理想塑性不可压缩,对此圆筒进行极限压力分析.
2.1弹性状态
由于外压为正,则径向正应力σρ为压应力,环向正应力σφ为拉应力,应力分布大致如图2所示.
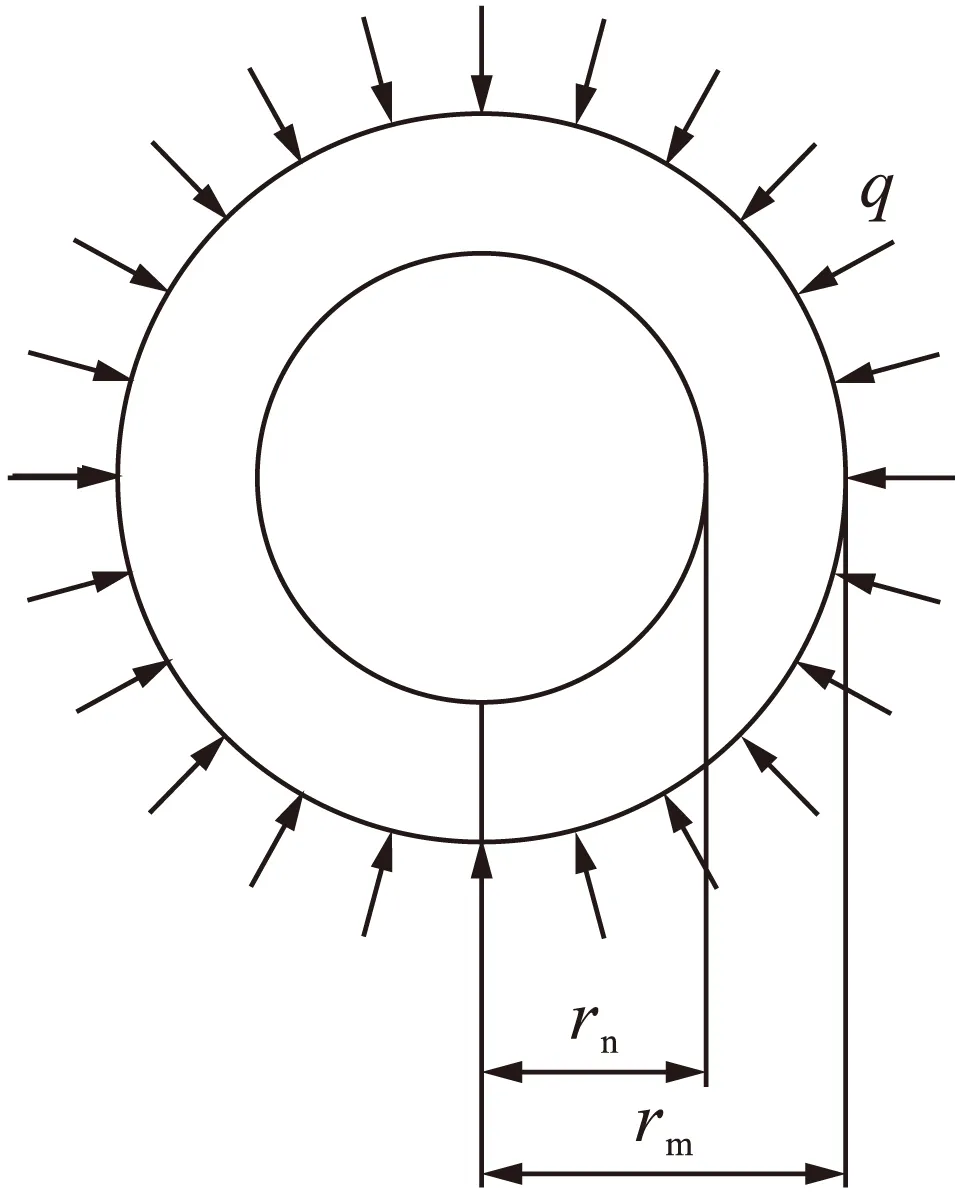
图1 厚壁圆筒模型Fig.1 Model for thick-wall cylinder
根据徐芝纶[12]的弹性力学解答可知其边界条件为

图2 应力分布Fig.2 Stress distribution
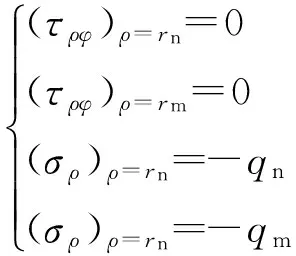
(4)
式中,ρ为厚壁圆筒的径向半径.进一步可求得在外压作用下其弹性解为

(5)
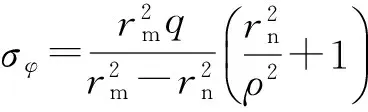
(6)
根据平面应变状态即εz=0可得
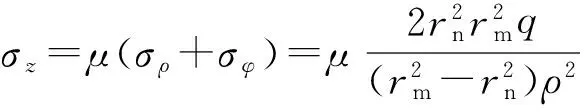
(7)
取μ=0.5,则式(7)可整理为
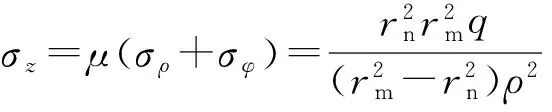
(8)
由式(4)~(6)可知
σ1=σφ≥σ2=σz≥σ3=σρ
(9)
将式(9)分别代入主剪应力的公式可得

(10)
将式(10)代入式(1)中的第一式整理可得
(11)
则弹性极限载荷为

(12)
式中:
应用统一强度理论求得的弹性极限载荷为
(13)
式中,b为反映中间主应力效应的参数.
2.2塑性区
随着均布载荷的继续增加,当均布载荷大于圆筒所能承受的弹性极限载荷,即q>qem时,圆筒的外壁将发生塑性变形,内壁附近仍然为弹性变形,且随着q的继续增加,塑性区将不断扩展,其模型如图3所示.
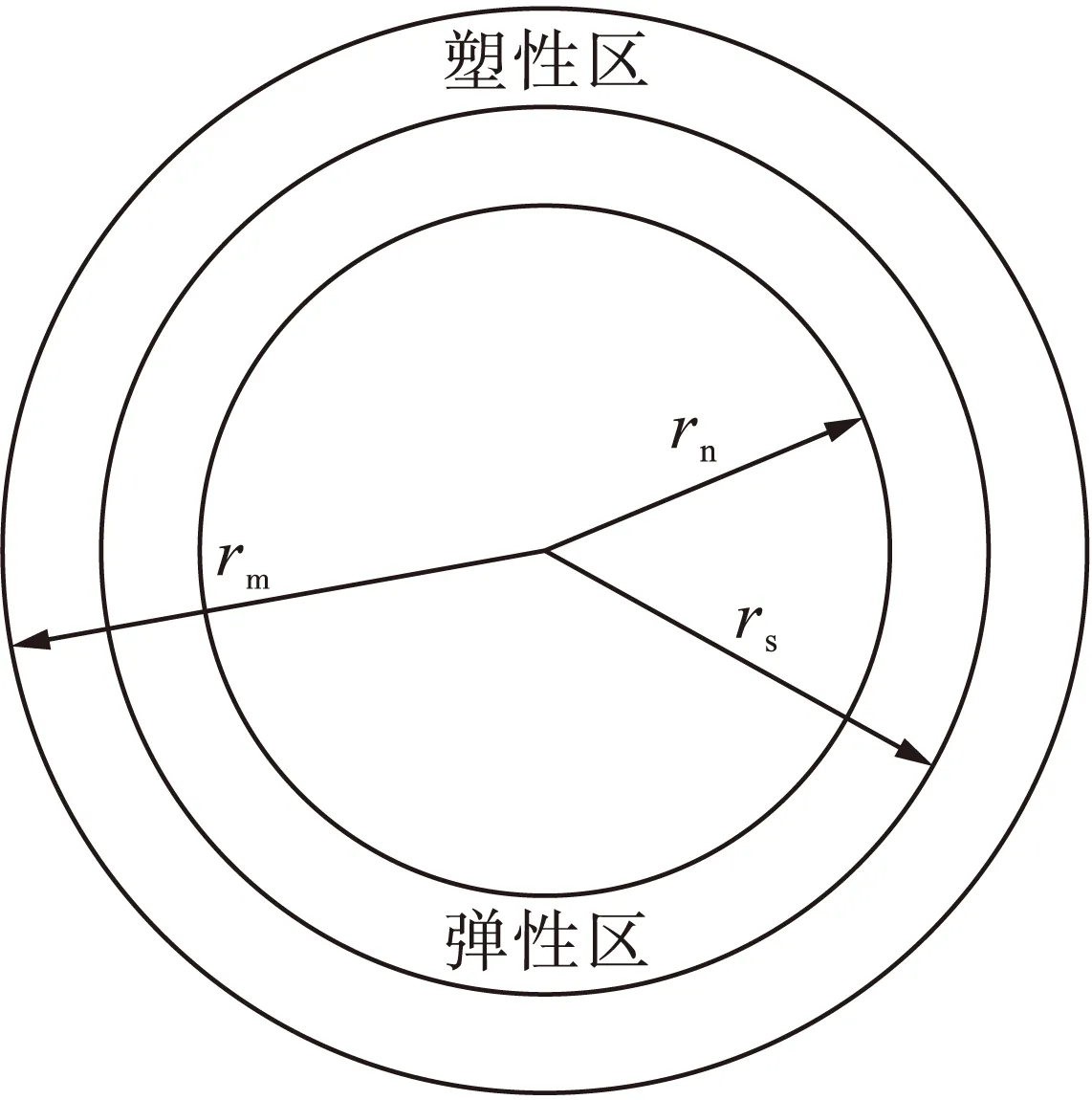
图3 弹塑性分析模型Fig.3 Elastic plastic analysis model
假定弹塑性区的半径为rs,将圆筒的弹性区和塑性区近似认为是两个圆筒,此时的外压为qa,rn≤r≤rs为弹性区,rs≤r≤rm为塑性区.在塑性区范围内应同时满足两个条件,分别为屈服条件与平衡方程,其平衡方程为
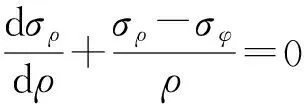
(14)
(15)
将式(15)代入式(14)中可得
(16)
根据边界条件
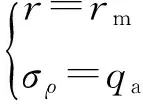
(17)
可解得其塑性区的应力为
(18)
而在弹性区rn≤r≤rs,应满足边界条件

(19)
且在r=rs处符合连续性条件,在r=rs处材料刚好发生屈服,计算可得弹性区的应力为
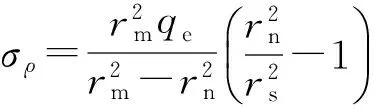
(20)
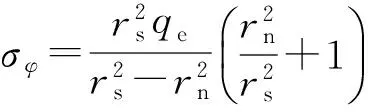
(21)
其中,将ρ=r=rs代入式(11)、(12),可得到qe,qe为应用本文理论求得的弹性极限载荷.
(22)
随着q的不断增大,塑性区不断向内扩展,当ρ=r=rn时,整个厚壁圆筒将全部处于塑性状态,此时,又称为全塑性状态.将r=rn代入式(22),可得到塑性极限载荷,即
(23)
应用统一强度理论求得的弹性极限载荷为
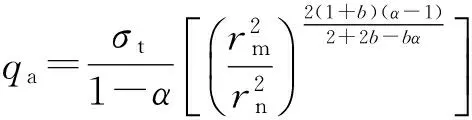
(24)
对于拉压同性材料其塑性极限载荷为
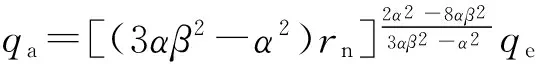
(25)
3 结 论
本文应用已提出的三参数双τ2强度理论对受均布外载荷作用下的厚壁圆筒进行了极限压力分析,得到其变形全过程的解析解,其结论如下:
1) 对拉压同性材料与拉压异性材料的厚壁圆筒进行了分析,得到了一个统一的理论表达式;
2) 通过引用的极限应力比α与β可知,厚壁圆筒的极限承载能力不仅与材料的拉伸强度有关,材料的极限压拉比α以及极限剪拉比β亦对其极限承载能力有一定影响;
3) 厚壁圆筒的极限承载能力与厚壁圆筒的半径有关,且给定不同材料的σt、极限应力比α与β即可得到不同材料的厚壁圆筒的极限压力.
[1]陈勇军,郑津洋,邓贵德,等.单层厚壁圆筒弹性动应力的简化计算方法 [J].工程力学,2006,23(11):45-51.
(CHEN Yong-jun,ZHENG Jin-yang,DENG Gui-de,et al.A simplified method for calculation elastodynamic stresses of monobloc thick-walled cylinder [J].Engineering Mechanics,2006,23(11):45-51.)
[2]朱国民,蔡钢思,高增梁,等.厚壁圆筒在内压和轴向力复合载荷作用下的极限载荷 [J].压力容器,2008,25(7):1-5.
(ZHU Guo-min,CAI Gang-si,GAO Zeng-liang,et al.Limit load solution for a thick-walled cylinder under cambined internal pressure and axial tension [J].Pressure Vessel Technology,2008,25(7):1-5.)
[3]陈昌富,肖淑君,杨宇.考虑应变软化厚壁圆筒受外压作用统一极限解 [J].湖南大学学报(自然科学版),2006,33(2):1-5.
(CHEN Chang-fu,XIAO Shu-jun,YANG Yu.Unified limit solution of thick wall cylinder subject to external pressure considering strain softening [J].Journal of Hunan University(Natural Sciences),2006,33(2):1-5.)
[4]Zhu X K,Leis B N.Average shear stress yield criterion and its application to plastic collapse analysis of pipelines [J].International Journal of Pressure Vessels and Piping,2006,83(9):663-671.
[5]Jin C W,Wang L Z,Zhang Y Q.Strength differential effect and influence of strength criterion on burst pre-ssure of thin-walled pipelines [J].Applied Mathema-tics and Mechanics,2012,33(11):1361-1370.
[6]杨宇宙,钱林方,徐亚栋,等.复合材料厚壁圆筒的疲劳损伤研究 [J].应用力学学报,2013,30(3):378-383.
(YANG Yu-zhou,QIAN Lin-fang,XU Ya-dong,et al.Fatigue failure analysis of composition material tube [J].Chinese Journal of Applied Mechanics,2013,30(3):378-383.)
[7]杨宇宙,钱林方.复合材料厚壁圆筒的损伤问题 [J].材料科学与工程学报,2012,30(2):256-262.
(YANG Yu-zhou,QIAN Lin-fang.Failure analysis of thick wall tube of carbon fiber/expoxy composite [J].Journal of Materials Science & Engineering,2012,30(2):256-262.)
[8]敖文刚,伍太宾.双剪统一强度理论在厚壁圆筒分析中的应用 [J].模具工业,2007,33(8):28-31.
(AO Wen-gang,WU Tai-bin.Application of double-shear unified strength theory of thick-walled cylinder [J].Die and Mould Industry,2007,33(8):28-31.)
[9]宁宝宽,黄杰,陈四利,等.广义双τ2强度理论在土压力计算中的应用 [J].沈阳工业大学学报,2009,31(6):708-711.
(NING Bao-kuan,HUANG Jie,CHEN Si-li,et al.General twinτ2strength theory for calculating earth pressure [J].Journal of Shenyang University of Technology,2009,31(6):708-711.)
[10]陈四利,俞秉义.双T2和双τ2屈服准则及其推广 [J].力学与实践,1994,16(5):60-62.
(CHEN Si-li,YU Bing-yi.TwinT2andτ2yield criteria and its generalization [J].Mechanics in Engineering,1994,16(5):60-62.)
[11]陈四利.双T2强度理论及其推广 [J].应用力学学报,1995,12(4):118-121.
(CHEN Si-li.TwinT2failure theory and its generation [J].Chinese Journal of Applied Mechanics,1995,12(4):118-121.)
[12]徐芝纶.弹性力学简明教程 [M].北京:高等教育出版社,1985.
(XU Zhi-lun.Concise tutorial on elasticity [M].Beijing:Higher Education Press,1985.)
(责任编辑:钟媛英文审校:尹淑英)
Limit stress analysis for thick-wall cylinder based on tri-parameter and twinτ2strength theory
CHEN Si-li, LI Yan-yu, ZHANG Jing-yu
(School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China)
In order to obtain the unitive analytical solution of whole elastic-plastic analysis process for the thick-wall cylinder prepared by two materials with the same tensile and compressive strengths as well as the different tensile and compressive strengths under the effect of uniformly distributed load, the elastic-plastic stress analysis for the thick-wall cylinder was carried out with the tri-parameter and twinτ2strength theory. Through quoting the limit stress ratioαandβin the tri-parameter twinτ2strength theory, the uniform analysis for the materials with the same tensile and compressive strengths as well as the different tensile and compressive strengths were performed. In addition, the elastic limit pressure and elastic-plastic limit pressure as well as the relationship between the stress in the elastic and plastic zone, limit stress ratioαandβof materials and elastic-plastic radius were obtained, respectively. The results show that not only the material limit stressσt, limit stress ratioαandβhave certain influence on the ultimate bearing capacity of thick-wall cylinder, but also the limit pressure of thick-wall cylinder is associated with its inside and outside radius.
uniformly distributed load; analytical solution; thick-wall cylinder; limit stress ratio; elastic-plastic stress; elastic limit pressure; elastic-plastic limit pressure
2015-11-03.
国家自然科学基金资助项目(51279109).
陈四利(1959-),男,辽宁绥中人,教授,博士,主要从事环境岩土工程材料理论与试验等方面的研究.
建筑工程
10.7688/j.issn.1000-1646.2016.05.14
TU 501
A
1000-1646(2016)05-0555-05
*本文已于2016-05-12 14∶01在中国知网优先数字出版. 网络出版地址:http:∥www.cnki.net/kcms/detail/21.1189.T.20160512.1401.040.html
