平面折展机构平面弹簧的设计与分析

刘　凯　曹　毅,2　丁　锐

1.江南大学，无锡，2141222.上海交通大学机械系统与振动国家重点实验室，上海，200240



平面折展机构平面弹簧的设计与分析

刘凯1曹毅1,2丁锐1

1.江南大学，无锡，2141222.上海交通大学机械系统与振动国家重点实验室，上海，200240

针对常规平面弹簧变形过程中运动端容易产生周向旋转从而造成振动和磨损的问题，设计了一种基于LEMs的平面弹簧，该弹簧由平面薄板加工成形且能实现平面外运动，具有体积小、易加工，结构简单及变形过程中运动端不发生周向旋转等优点。首先，基于悬臂梁模型和伪刚体模型分别推导了LEMs平面弹簧的刚度计算公式。其次，为验证所推导公式的正确性，建立了LEMs平面弹簧的ANSYS仿真模型，并将有限元分析结果与上述两种理论模型的计算结果进行了对比。结果表明，在变形较小的情况下由悬臂梁模型所推导的公式计算精度更高，在变形较大的情况下使用由伪刚体模型所推导的公式更为合适。最后，通过大量实例分析推导了两个公式的适用范围，并用一组数值算例证明了其正确性。

平面折展机构；平面弹簧；伪刚体模型；有限元分析

0　引言

LEMs是一种从平面材料中加工成形，且能实现平面外运动的新兴柔顺机构[1]，它属于平面正交机构、变胞机构及柔顺机构的范畴，因此也聚集了这三类机构的优势：能以简单的拓扑结构实现复杂的机械运动；加工工艺简单、经济；其平面特性能降低运输及储藏成本。

目前，对LEMs的研究主要集中于柔性机构及其铰链的设计。Wilding等[2]将球面机构和LEMs简洁紧凑的特性相结合，综合出了21种球面LEMs四杆机构；王涛[3]针对已有的LEMs四杆机构，研究了各特征参数对LEMs四杆机构性能的影响；邱丽芳等[4]设计了一种新型平面折展机构柔性铰链并分析了其等效刚度。通过诸多学者的努力，LEMs技术已经发展成为能应用于商业产品并实现特定功能的科学技术，尤其适用于MEMS(micro electro mechanical systems)设计，如投影机、显示镜的驱动系统，光调幅器。此外，LEMs的特性也使其能应用于平面弹簧。

平面弹簧是能在平面中制造或能压缩成平面的弹簧。目前较为常见的平面弹簧包括星架弹簧、涡卷弹簧、碟形弹簧以及S形和C形等平面微弹簧。平面弹簧的主要优点是结构简单，且在初始状态或被压缩状态占用的空间少。但平面弹簧也有不少缺点，如在受力变形过程中会产生周向旋转，使固定于弹簧运动端上的构件伴随弹簧运动端转动，若构件未固定于运动端，则两个部分会发生相对滑动，从而产生磨损、振动及噪声。当前已有不少国内外学者对平面弹簧作了大量研究。王超等[5]设计了一种基于平面矩形螺旋梁结构的平面微弹簧；吴佳俊等[6]以非接触式形状记忆合金平面涡卷弹簧为例，通过研究动作原理，建立了弹簧的力学模型并用实验证明了其正确性；周织建等[7]提出了一种MEMS平面S形锥形弹簧并对其进行了特性分析；李华等[8]建立了MEMS平面微弹簧的力学模型并对其进行了刚度分析；吴志亮等[9]对L形弹簧进行了分析计算，并得到理论计算公式；Kim等[10]将L形弹簧合理运用于抗屈服变形探针上，改善了其受压稳定性。综上所述，目前大部分的平面弹簧只能用于承受平面内的力的场合，而对于能承受面外力的平面弹簧，又存在变形过程中运动端容易产生周向旋转，从而引起摩擦、磨损的问题。

针对上述问题，本文基于LEMs设计了一种结构紧凑、加工方便的平面弹簧，该平面弹簧在变形过程中运动端无周向旋转，能减少弹簧的摩擦、磨损；其次基于悬臂梁模型和伪刚体模型[11]分别推导了LEMs平面弹簧的刚度计算公式，并利用ANSYS验证了两种公式的正确性。最后，通过大量实例分析计算确定了两种公式的适用范围，并验证了其有效性。

1　结构设计

根据LEMs特性设计的LEMs平面弹簧的结构如图1所示。圆环基座与运动平台通过4组片段连接形成整体，其中每组片段由三个柔性片段和两个连接片段组成，它们依次呈90°度交替连接，形成图2所示的“之”字形折返运动关节，4组“之”字形折返运动关节在圆环基座与运动平台间放射式均匀分布，将圆环基座和运动平台连接成整体，且4组片段间形成4块镂空区域。图2中，L、b分别为柔性片段的长度和宽度，B为柔性片段间的间距，D为连接片段厚度，d为柔性片段厚度,它们的单位为mm。

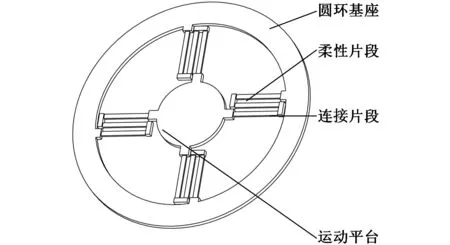
图1　LEMs平面弹簧结构示意图

(a) 运动关节俯视图

(b) 运动关节剖视图图2　弹簧运动关节

LEMs平面弹簧的工作原理可以描述为：在工作过程中，圆环基座固定，运动平台受垂直平面的均布力作用“浮出”制造平面，此时“之”字形折返运动关节发生变形并产生一个反作用力。由于柔性片段的刚度远小于连接片段刚度，故平面弹簧的变形仅发生于柔性片段。此外，4组“之”字形折返运动关节在圆环基座与运动平台间呈放射式均匀分布，使运动平台所受的合力方向垂直于制造平面，故其动作过程必然为垂直平面的直线运动而无周向旋转。

2　理论分析

2.1悬臂梁模型

若LEMs平面弹簧的变形在线性范围之内，可运用悬臂梁变形计算模型对弹簧的线性位移进行分析求解，进而根据线性弹性理论得到LEMs平面弹簧的刚度计算公式。

由于4组运动关节均匀分布，故仅对其中一组运动关节进行分析。假设均布载荷P垂直作用于运动平台，则其中一组运动关节所受的力F=0.25P，受力后LEMs平面弹簧的运动关节主要产生弯曲变形及扭转变形，其中弯曲变形量是柔性片段相对固定端的偏移量，可以表示为[12]

(1)

(2)

式中，δ为垂直方向的变形量；c为比例因子，由末端约束决定，此处固定-导向梁c取12；E为材料的弹性模量；Is为柔性片段的惯性矩[13]。

扭转变形量是柔性片段的扭转角度，可表示为[13]

(3)

Ip=βbd3

(4)

式中，M为柔性片段所受扭矩；G为切变模量，ν为泊松比；Ip为极惯性矩[13]；β为与柔性片段截面边长比b/d相关的系数，可通过查表得到[13]。

LEMs平面弹簧的“之”字形折返运动关节受力模型可简化为图3所示模型。

图3　运动关节受力简化模型

运动关节中柔性片段AB、CD、EH的长度均相等，且它们的刚度远小于连接片段BC、DE的刚度，因此连接片段可以视为刚体。点H处的总位移δ1由柔性片段的弯曲和扭转倾斜造成，因此：

δ1=δAB+δCD+δEH+δ′

(5)

其中，δAB=δCD=δEH，由柔性片段弯曲形成，计算公式为

(6)

δ′为柔性片段扭转导致连接片段倾斜所引起的H点位移，其中扭转变形主要发生在柔性片段AB及EH，故根据式(3)得

(7)

总位移δ1为

(8)

根据线弹性理论[13]，LEMs平面弹簧的刚度为

(9)

2.2伪刚体模型

当LEMs平面弹簧的变形量较大时可以用固定-导向伪刚体模型分析其变形。

末端受载荷作用的固定-导向伪刚体模型如图4所示，梁的一端被固定，而另一端被导向，即使该梁的末端角度保持水平不变。由于末端要保持一个固定角度，因此末端必有相应的力矩(图4中的M0)，故所得梁的变形形状关于中心线反对称。

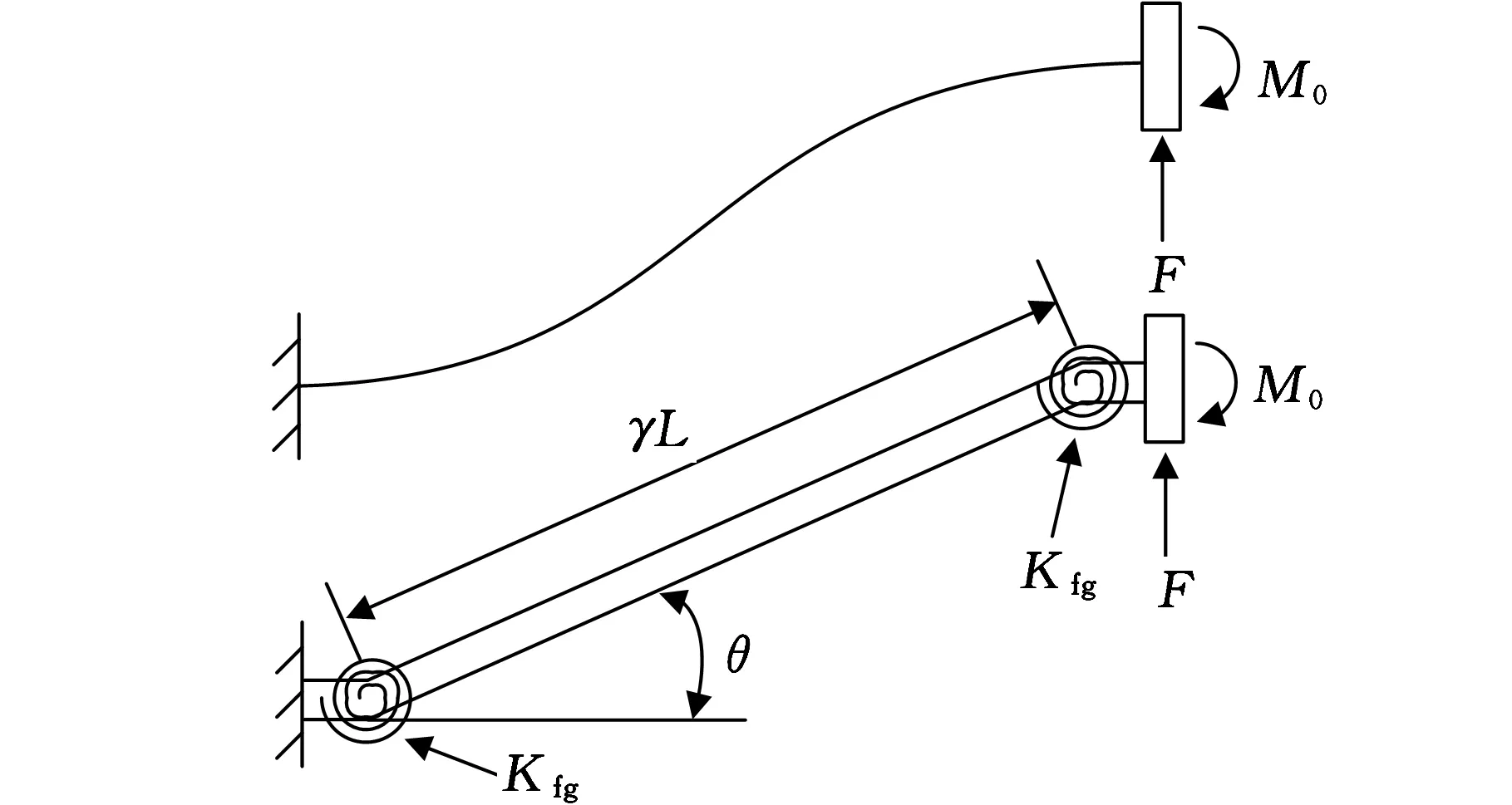
图4　固定-导向伪刚体模型

在固定-导向伪刚体模型中，扭簧刚度系数Kfg可采用下式表示[11]：

(10)

式(10)中，γ和Kθ通常采用近似值，γ=0.85，Kθ=2.68。

固定-导向梁在垂直力作用下的位移可以表示为

δv=γLsinθ

(11)

伪刚体角θ与扭簧所受转矩有关，即

γFLcosθ=2Kfgθ

(12)

将cosθ的泰勒展开公式代入式(12)得

γFLθ2+4Kfgθ-2γFL=0

(13)

求解式(13)中的θ：

(14)

由柔性片段扭转造成的H点位移为

(15)

其中，Ki为扭转变形处的截面形状相关参数，可由文献[14]提出的精度较高且不受宽厚比影响的公式求解：

(16)

联立式(11)、式(14)和式(15)可得关节H点的总位移δ2：

(17)

故根据伪刚体模型推导的LEMs平面弹簧的刚度为

(18)

由上式分析可知，LEMs平面弹簧的刚度与受力之间成非线性关系。

3　仿真验证与适用范围

为验证上述悬臂梁理论模型与伪刚体理论模型所推导刚度计算公式的正确性，设计了LEMs平面弹簧实例。由于该LEMs平面弹簧结构对称，为了减小ANSYS软件的分析计算量，取LEMs平面弹簧的其中一个运动关节进行建模分析，然后将有限元分析结果与上述两种理论模型的计算结果进行对比。

所设计实例的结构参数如下：L=10mm， B=1mm，b=1mm，d=0.4mm。本例中选择强度与弹性模量之比较高的ABS工程塑料作为LEMs平面弹簧的材料，其弹性模量E=2.2GPa，泊松比ν=0.34，屈服极限σmax=70MPa。考虑弹簧变形需在弹性范围之内，故施加的力P不超过Pmax=1.5N，即每个运动关节受力不超过0.375N，其中Pmax可由下式求得

(19)

如图5a所示，仿真模型包含2392个六面体单元，其一端添加固定约束，另一端添加“导向”约束，并施加一个垂直平面的力。当加载的力为0.01N，即平面弹簧受力P=0.04N时，由ANSYS分析所得的LEMs平面弹簧运动关节的受力变形，如图5b所示，由图可知弹簧的变形量δ0=0.291mm，而利用悬臂梁模型推导的式(9)求得的弹簧变形量δ1=0.274mm，基于伪刚体模型推导的式(18)求得弹簧的变形量δ2= 0.266mm。选则大小不同的力，可以得到如表1

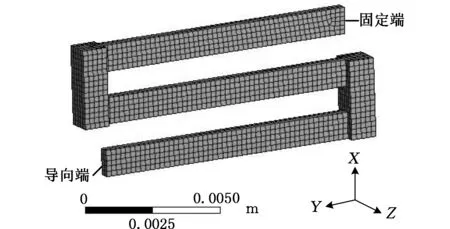
(a)运动关节网格划分图

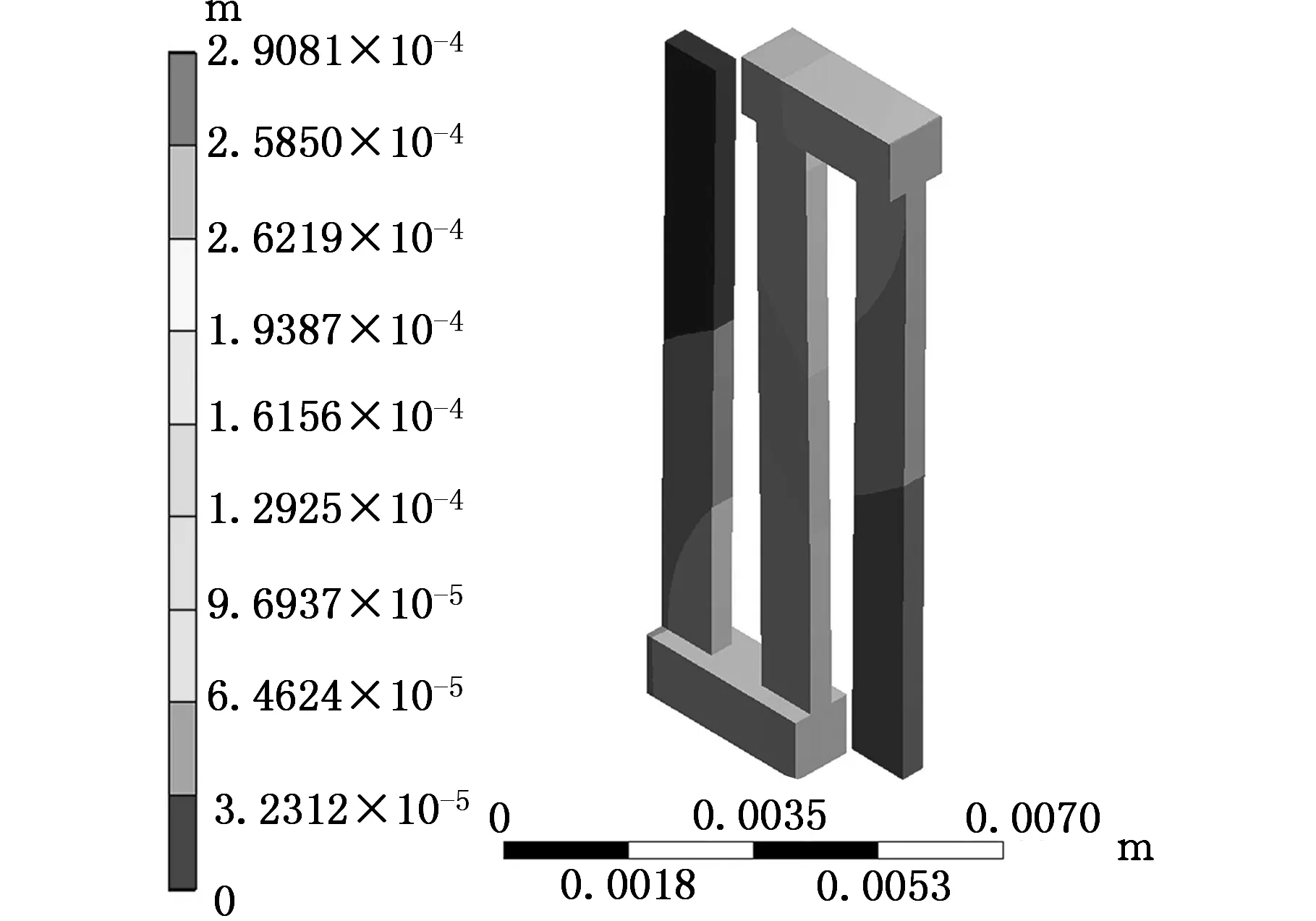
(b)运动关节变形云图图5　运动关节有限元仿真模型

所示的计算分析结果。为了更加直观地表示LEMs平面弹簧受力与变形量之间的关系，用MATLAB软件绘制得到如图6所示的变形曲线及如图7所示的相对误差曲线。

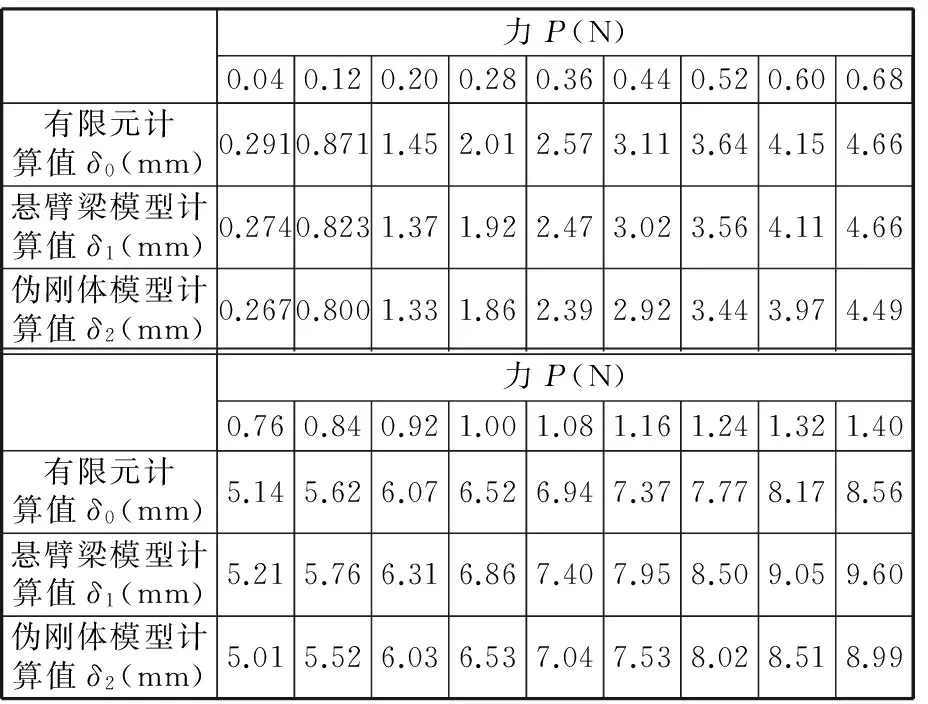
表1　有限元、悬臂梁模型及伪刚体模型的计算值

图6　LEMs平面弹簧三个变形量计算值随力的变化曲线

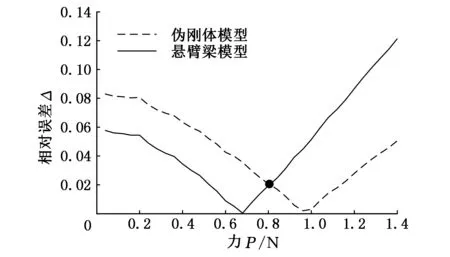
图7　悬臂梁模型与伪刚体模型计算值相对误差

由图6和图7分析发现：伪刚体模型计算值和悬臂梁模型计算值基本与有限元分析结果相吻合；在作用力较小，即变形相对较小的情况下悬臂梁模型的计算值更精确，LEMs平面弹簧的刚度用悬臂梁模型推导的式(9)表示更准确；在作用力较大的情况下，伪刚体模型的计算值精确度要高一些，LEMs平面弹簧的刚度用伪刚体模型推导的式(18)表示更精确。综上所述，为提高LEMs平面弹簧的刚度理论计算精度，需进一步研究两种刚度计算公式的适用范围。

进一步的研究表明，当加载的力P与最大可加载力Pmax之比达到某个值后(如图7所示黑点)，伪刚体模型的计算值精度将开始高于悬臂梁模型计算值，而该比值与L/b成正比，与d/b的平方成反比。其中，Pmax可用式(19)计算。

为了推导两种公式的适用范围，设计了32组实例，其结构尺寸比例如下：L/b=7，9，11，13，15，17，19，21；d/b=0.25，0.40，0.50，0.67。选出伪刚体模型计算值精度开始高于悬臂梁模型计算值的力Pa，将Pa/Pmax的比值a记录于表2。

表2　Pa/Pmax比值

将表2中的数据导入MATLAB，以L/b、d2/b2为自变量，a为因变量得到如图8所示的图形，从图8中可以发现在L/b、d2/b2不同的情况下，a的值都近似在同一个空间平面内。利用OriginPro软件求得上述近似空间平面的多元线性回方程：

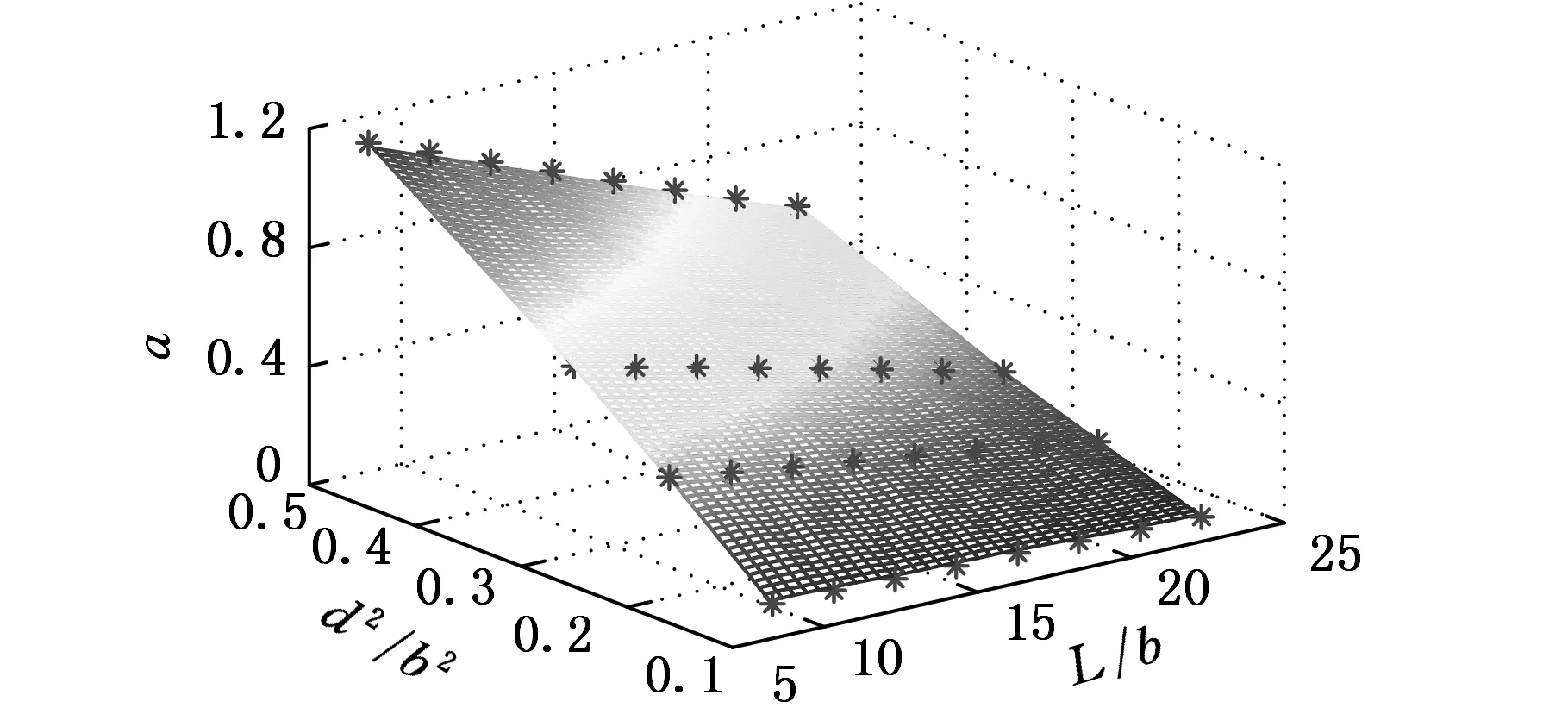
图8　Pa/Pmax比值分布

(20)其中，多元线性回归方程的R2值为0.9507，F值为299.9279，P值为0。上述分析表明，表2中的数据与多元线性回归方程的拟合度较高，且两种模型推得的刚度计算公式在力为Pa附近通常计算精度都较高，Pa/Pmax可以用式(20)表示。故当施加在弹簧上的力小于Pa时，LEMs平面弹簧的刚度可以用悬臂梁模型推得的式(9)表示；当施加在弹簧上的力大于Pa时，弹簧的刚度可以用伪刚体模型推得的式(18)表示。

将上述结论总结如下：

由于在Pa附近两个模型推得的刚度计算公式精度都较高，故上述公式的区间都取了等号。

为证明上述结论的正确性，以第3节实例为例，此时a=0.4682，Pmax=1.5 N，当P≤Pa=0.7 N时，k=k1，误差在0与5.84%之间；当P≥Pa=0.7 N时，k=k2，误差在0.153%与5.02%之间，总体误差在0到5.84%之间。但只用悬臂梁模型推得的计算公式k=k1，最大误差将达12.15%；而仅用伪刚体模型推得的计算公式k=k2，误差在0.153%到8.59%范围内，如表3所示。显然区分两个公式的适用范围，可以提高LEMs平面弹簧刚度的计算精度。上述分析进一步验证了公式适用范围的正确性。

表3 误差对比　%

4　结论

(1) 本文设计了一种LEMs平面弹簧，解决了传统平面弹簧在变形过程中运动端产生周向旋转从而造成磨损和振动的问题。

(2) 基于悬臂梁模型与伪刚体模型，分别推导了LEMs平面弹簧的刚度计算公式。

(3) 通过ANSYS有限元分析实例验证了两种刚度计算公式的正确性，然后基于大量分析计算，总结了两种公式的适用范围，并证明了其有效性。

(4)在此基础上，后续工作将推导非对称载荷作用下LEMs平面弹簧的理论计算模型并加工实物进行实验分析。

[1]Jacobsen J O, Winder B G, Howell L L. Lamina Emergent Mechanisms and Their Basic Elements[J]. Journal of Mechanisms and Robotics, 2010,2(1):1-9.

[2]Wilding S E, Howell L L, Magleby S P. Spherical Lamina Emergent Mechanisms[J]. Mechanism and Machine Theory, 2012,49:187-197.

[3]王涛. LEMs四杆机构的分析及其特性参数的研究[D]. 北京：北京科技大学, 2012.

[4]邱丽芳, 韦志鸿, 徐金梧. 新型平面折展机构柔性铰链等效刚度分析[J]. 机械工程学报, 2014,50(17):25-30.Qiu Lifang, Wei Zhihong, Xu Jinwu. Analysis of Equivalent Stiffness of New LEMs Flexure Hinge[J]. Journal of Mechanical Engineering. 2014, 50(17):25-30.

[5]王超, 陈光焱, 吴嘉丽. 用于低gn值微惯性开关的低刚度平面微弹簧设计与制作[J]. 光学精密工程, 2011,19(3):620-627. Wang Chao, ChenGuangyan, Wu Jiali. Development of Planar Micro-spring with Low Stiffness in Low-gnMicro Inertial Switch[J]. Optics and Precision Engineering, 2011,19(3):620-627.

[6]吴佳俊, 王帮峰, 芦吉云,等. 镍钛诺合金涡卷弹簧的力学建模与测试[J]. 光学精密工程, 2014,22(4):963-969.

Wu Jiajun, Wang Bangfeng, Lu Jiyun, et al. Mechanical Modeling and Test If Nitinol Spiral Spring[J]. Optics and Precision Engineering, 2014,22(4):963-969.

[7]周织建, 聂伟荣, 席占稳,等. MEMS平面S形锥形弹簧的特性分析研究[J]. 微电子学, 2014,44(4):559-594.

Zhou Zhijian, Nie Weirong, Xi Zhanwen, et al. Study on Characteristics of MEMS Planar S-Form Conical Spring[J]. Microelectronics, 2014,44(4):559-594.

[8]李华, 石庚辰. MEMS平面微弹簧刚度分析[J]. 压电与声光, 2007,29(2):237-239.

Li Hua, Shi Gengchen. The Stiffness Analysis of MEMS Planar Microspring[J]. Piezoelectrics and Acoustooptics, 2007,29(2):237-239.

[9]吴志亮, 常娟, 冯鹏洲, 等. 引信用MEMS 平面微弹簧弹性系数分析[J]. 南京理工大学学报(自然科学版),2008,32(2):140-141.

WuZhiliang, Chang Juan, Feng Pengzhou, et al. Elastic Coefficient Analysis of MEMS Planar Microspring Used in Fuse[J]. Journal of Nanjing University of Science and Technology (Natural Science), 2008,32(2):140-141.

[10]Kim J Y, Lee H J, Cho Y H. Anti-buckling S-shapedVertical Microprobes with Branch Springs[J]. Microelectronic Engineering, 2010,87(9):1769-1776.

[11]豪厄尔.柔顺机构学[M]. 余跃庆,译. 北京: 高等教育出版社,2007.

[12]周慧. LEMs柔性铰链的分析与研究[D]. 北京: 北京科技大学,2012.

[13]刘鸿文. 材料力学[M]. 北京: 高等教育出版社.2004.

[14]Chen G, Howell L L. Two General Solutions of Torsional Compliance for Variable Rectangular Cross-section Hinges in Compliant Mechanisms[J]. Precision Engineering, 2009,33(3):268-274.

(编辑袁兴玲)

Design and Analysis of LEMs Planar Springs

Liu Kai1Cao Yi1,2Ding Rui1

1. Jiangnan University, Wuxi, Jiangsu,214122 2.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University, Shanghai, 200240

To avoid vibrations and abrasions caused by the rotation of a planar spring in the deformation processes, a new planar spring was proposed based on LEMs. The planar spring with advantages including a small volume, easy to fabricate, a simple structure and no revolution during the deformation, etc. might be fabricated from planar materials and might emerge out of the fabricated planar materials. Firstly, the stiffness of the planar spring was deduced based on the flexural cantilever model and the pseudo-rigid-body model respectively. In order to verify the correctness of the theoretical stiffness formulations, the ANSYS model for this planar spring was established and the FEA was compared with theoretical results calculated by the flexural cantilever model and the pseudo-rigid-body model, respectively. The results indicate that the formula derived from model of cantilever leads to the calculation with higher accuracy when the deformation is small. In contrary, the formula derived from pseudo-rigid-body model applying to large deformation is better. Finally, the applicable ranges for the two above mentioned models were analyzed separately and a numerical example was given to demonstrate their correctness.

lamina emergent mechanisms(LEMs); planar spring; pseudo-rigid-body model; finite element analysis(FEA)

2016-11-30

国家自然科学基金资助项目(50905075);江苏省“六大人才高峰”资助项目(ZBZZ-012);机械系统与振动国家重点实验室开放课题资助项目(MSV201407);江苏省食品先进制造装备技术重点实验室开放课题资助项目(FM-201402)

TH122

10.3969/j.issn.1004-132X.2016.19.018

刘凯，男，1991年生。江南大学机械工程学院硕士研究生。主要研究方向为柔顺机构学。曹毅，男，1974年生。江南大学机械工程学院副教授，上海交通大学机械系统与振动国家重点实验室访问学者。丁锐，男，1992年生。江南大学机械工程学院硕士研究生。