过盈配合单向分形界面微观接触面积研究
2016-10-19易利祥刘光复杜晓东
沈 健 易利祥 周 丹 刘光复 杜晓东
合肥工业大学,合肥,230009
过盈配合单向分形界面微观接触面积研究
沈健易利祥周丹刘光复杜晓东
合肥工业大学,合肥,230009
通过对模拟压缩机叶轮和轴过盈配合的试件表面轮廓进行分析,发现切削加工的粗糙配合表面具有单向粗糙度特征,同时垂直加工纹理方向的表面轮廓具有明显分形特性。基于M-B分形接触的修正模型,建立了具有单向粗糙度分形特征表面的理论接触模型,推导出接触面积与法向载荷的函数关系式。结合真实粗糙表面,建立了具有分形特性的单向粗糙度实体模型,利用有限元分析软件对实体模型进行了仿真分析,验证了接触面积与法向载荷函数关系的正确性。
过盈配合;微观表面;接触模型;分形
0 引言
压缩机的主轴和叶轮采用过盈配合的连接方式。为保证叶轮在高速旋转时,离心力产生的松动量不会导致轴和叶轮之间的过盈配合失效,叶轮与主轴必须有足够的过盈量。显然,随着过盈量的增大,叶轮与轴接触面上的应力也会增大[1]。在微观层面上,配合接触面上的较高微凸体在接触应力的作用下率先接触并发生变形,当接触应力持续增大,较低微凸体也进入接触并发生变形,接触微凸体的数量及接触面积增大。而配合界面的摩擦因数、磨损率等因素均与接触面积有关[2-3],配合界面的摩擦因数对过盈配合的设计计算起了至关重要的作用,在过盈配合拆解时,接触界面的损伤也与配合面的接触面积有着密切关系,所以对过盈配合界面接触面积进行研究有着重要的意义。Majumdar等[4-5]将分形理论引用到接触界面的研究中,形成了M-B弹塑性接触数学模型,该模型经过多年的研究,被广泛地运用到接触界面来计算摩擦和磨损、接触刚度和弹塑性变形等[6-7]。该模型在理论分析中,推导微凸体接触面积的分布函数时,认为总接触面积与最大微凸体接触面积的比值为1,这显然是不合理的,并且这种模型假设粗糙表面的粗糙度是各向同性的,然而实际切削加工的粗糙表面的粗糙度及分形特征是各向异性的。
本文将张长军等[8]、付秀娟[9]建立的具有单向粗糙度特征表面的弹塑性接触理论模型与Wang等[10]提出的M-B修正分形接触模型相结合,得到修正后的单向粗糙度特征分形接触模型,并导出了接触面积的理论计算公式。同时,结合真实粗糙表面建立具有分形特性的单向粗糙度实体模型,利用有限元分析软件ANSYS对该实体接触模型进行仿真分析。通过在模型的法向施加一定的载荷来模拟压缩机叶轮与轴过盈配合界面的接触应力,以验证具有单向粗糙度特征的分形接触理论模型的正确性。
1 具有单向粗糙度的分形接触模型
1.1单个微凸体的弹塑性接触状态
文献[11-12]考察了两个粗糙表面微凸体的接触情况,得到的结论是:两个粗糙面的接触与一个光滑刚性面和一个粗糙面的接触相差不大。所以本文将两粗糙表面的接触简化为等效粗糙表面与理想刚性光滑平面的接触,如图1所示。

图1 简化的接触模型
为了进一步研究接触面上单个微凸体的微观接触状态,将每一个微凸体的接触简化为一个刚性平面和圆柱体的接触,如图2所示。简化后的接触面上单个微凸体的接触点为规则的矩形,矩形的宽度l将由零变化到最大宽度l1。

图2 单个微凸体的接触状态
根据图2分析单个微凸体的接触情况,R为微凸体顶部的曲率半径,B为接触平面平行于粗糙纹理方向上的宏观尺寸,l 为在载荷p作用下接触矩形的宽度。结合Majumdar和Bhushan的研究成果,分形表面的接触尺寸与微凸体顶部曲率半径存在如下关系[4]:
(1)
式中,D0为x方向上的轮廓线的分形维数;G为轮廓幅值的尺度系,m。
用lc表示微凸体从弹性变形到塑性变形临界接触长度,则圆柱面发生塑性变形的简化判据为[9]
(2)
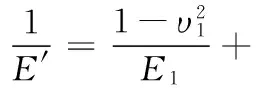

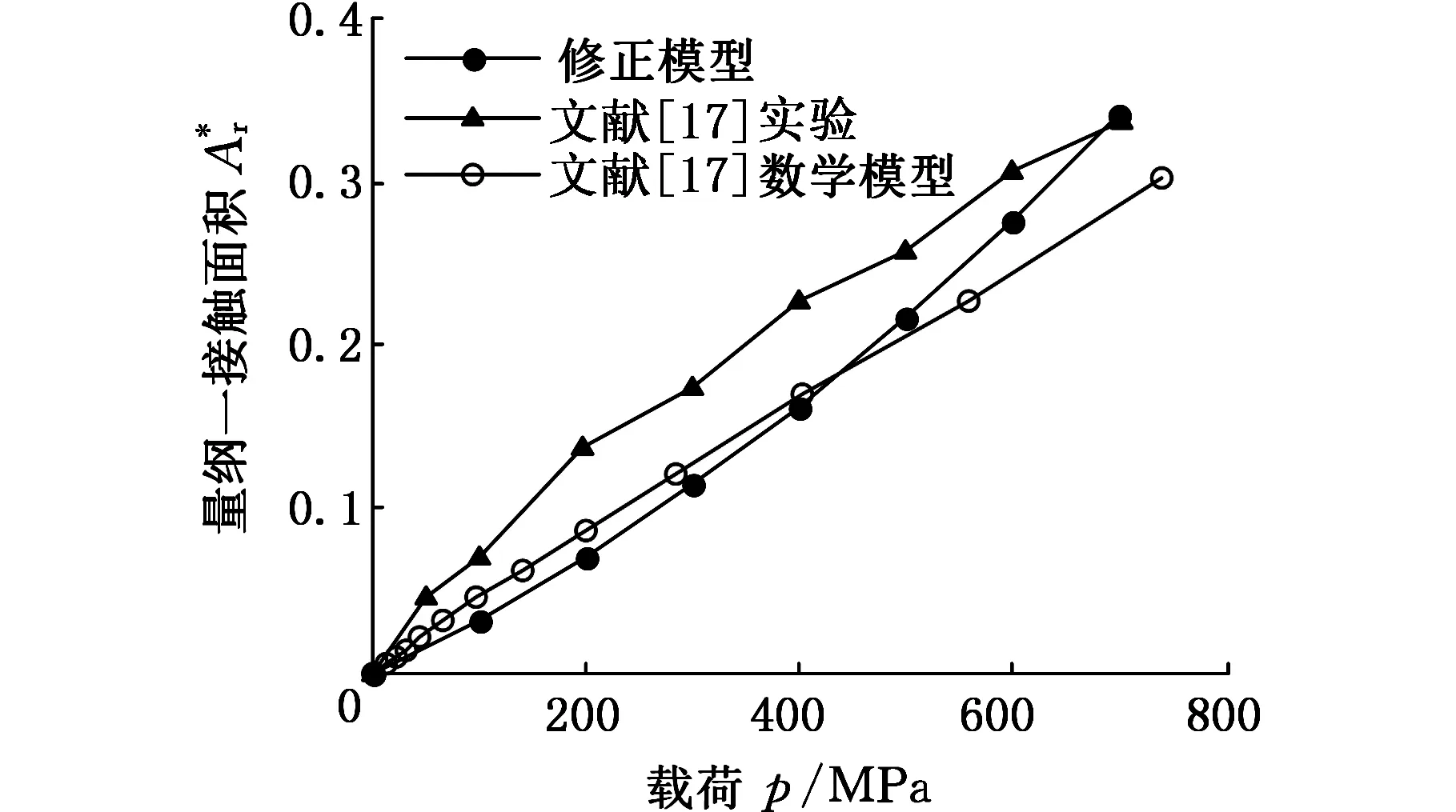
当l>lc时,圆柱形微凸体的接触区域发生弹性变形;当l 决于试件表面的分形参数D0、G 和试件材料的机械力学性能,不受载荷和微凸体形状尺寸的影响。 当l>lc时,弹性接触区域的载荷为[9] (3) 当l pp=σBl (4) 1.2微凸体的接触面积分布 根据Wang和Komvopoulos的研究[10],对M-B接触模型中微接触点面积大小分布函数进行修正,微凸体接触点面积A超过a值的数量N与a之间满足幂率关系,表示如下[13]: (5) 其中,D1为各向同性粗糙表面轮廓的分形维数,k0为比例系数。将式(5)变为 (6) 式(6)只有在Dx=Dy时,即针对各向同性的粗糙表面时才成立,这时在任意方向上的接触点的数量也应该是相同的[8],即Nx=Ny: N(A>a)=Nx(L>l)Ny(L>l) (7) 通过比较可得任意方向的接触点数量为 (8) (9) 式中,ψ为域扩展系数,是关于D的函数。 1.3理论接触面积与法向载荷的关系 通过式(9)得出理论接触面积: (10) 由式(10)可得 从而修正了原模型中分形维数趋近于1时,总接触面积和最大微凸体接触面比值为1的不合理性。 接触面上的总载荷等于每个接触点上的分载荷的总和: (11) 将式(3)、式(4)、式(9)代入式(11)中可得法向载荷与接触面积的量纲一参数关系表达式如下: (12) 2.1试件表面三维形貌测量 本文以西气东输大型离心式压缩机的叶轮和轴的过盈配合界面为研究对象。采用轴相同的材料40CrNiMo7,选用与实际叶轮轴相同的加工方式,最后一道加工工序为精磨,制成与叶轮轴表面加工纹理相同、粗糙度值相近,且表面纹理均匀的试件。在光洁、没有肉眼可辨划痕的试件表面上选取面积为100 μm×100 μm的区域进行三维形貌测量,如图3所示。 图3 采样区域三维形貌图 从图3可以看出,磨削试件的表面具有方向性,平行于表面加工纹理方向的粗糙度值只有垂直于加工纹理方向的粗糙度值的十分之一左右,数值相差较大。所以,可以认为该表面是具有单向粗糙度的表面。 2.2垂直试件加工纹理方向的分形特性 运用结构函数法,对试件表面垂直于纹理方向轮廓的分形特性进行验证。采用瑞士Trimos-3L型形貌仪对试件上三个不同位置的轮廓曲线进行提取,采样长度为4 mm,采样间隔Δt=0.1μm,N1是数据点的个数,轮廓数据点高度Z(xi)=Zi(i=1,2,…,N1),令ε=nΔt(n=1,2,…,N1),则结构函数表达式如下: (13) 求出结构函数S(ε),在双对数lgS(ε)~lgε坐标系中整理数据,如图4所示。 图4 试件表面轮廓结构函数与尺度的对数关系 从图4可以看出,轮廓曲线的结构函数的对数和尺度的对数关系近似呈线性关系,这说明垂直加工纹理方向的表面轮廓具有良好的分形特性[5]。将图中的多条曲线近似直线拟合,得到式(14)的直线方程,由此可以验证试件原始表面的分形特性,数据直线拟合得到: lgS(ε)=1.345lgε-2.53 (14) 根据以下两式分别计算出分形维数D和分形尺度系数G: D=(4-k1)/2 (15) (16) 式(15)、式(16)中,k1是式(14)拟合直线的斜率,A1是该直线在纵轴上的截距,γ=1.5,把式(14)中的斜率和截距代入式(15)和式(16),分别计算出 D=1.345,G=2.05×10-13m。 2.3载荷与接触面积的理论计算公式 试件的名义接触尺寸为10 mm×10 mm,则B=10 mm,试件材料的机械性能如表1 所示。将相关的数据值代入式(12),可得修正后的压缩机叶轮和轴过盈配合单向分形表面的接触面积和载荷的计算公式: (17) 表1 叶轮和轴材料的机械性能参数 图5 载荷与接触面积比例的关系 从图5中可以看出,原模型和修正模型的接触面积比例均随着载荷的增大而增大,两者近似为线性关系,此关系符合摩擦学中粗糙表面的接触情况[10]。同时,修正的接触面积比例大于原理论的接触面积比例,并且差值随着载荷增大而增大,当载荷较小,p=100 MPa时,接触面积比例差值最小为7.73%,当载荷较大,p=500 MPa时,接触面积比例差值最大为17.3%。通过对比,从式(9)即修正的微凸体分布函数与原理论的分布函数得到na(l)/no(l)=ψ(2-D)/2>1,即相同的接触宽度,修正的模型中发生接触的微凸体数量较多,所以如果要达到相同的接触面积,修正模型所需要的载荷较小。另一方面,当载荷较大时,同样的载荷下,由于原理论模型中承载的微凸体较少,单个接触微凸体的接触载荷较大,相应的变形量也会较大,会率先进入塑性变形的状态,所以修正模型和原模型接触面积的差值会随着载荷的增大而增大。 3.1有限元仿真分析 将轴和叶轮的过盈配合接触界面简化为光滑平面实体与等效粗糙表面实体的接触。实际加工表面是具有单向粗糙度的表面,在较小范围内,通过对比发现,一定间隔的垂直加工纹路的粗糙度轮廓曲线基本重合。因此,为简化模型和降低计算复杂程度,可以将测得的一维表面轮廓曲线在三维软件中拉伸生成实体等效作为粗糙表面实体,如图6a所示。将模型导入到有限元软件ANSYS中模拟计算时,为了加速收敛,提高计算精度,对网格进一步修整,考虑到接触主要发生在表面,所以对表面接触区域进行加密处理,如图6b所示。 (a) 粗糙表面实体 (b)加密处理图6 接触实体模型及网格划分 过盈配合界面上受力状态复杂,法向接触应力沿着轴线方向分布不均。离心式的压缩机叶轮与轴的设计过盈量为轴直径的0.17%~0.22%,属于大过盈配合,与φ225H7/y6相当。经过分析,该型压缩机叶轮和轴的设计过盈量为轴直径的0.22%时,配合界面上的最大法向接触应力为253.27 MPa[15],本文用法向接触载荷代替过盈量进行分析,为适当地扩大探讨范围,接触应力值选为100,200,300,400,500 MPa,法向载荷与过盈量的对应数值关系可以通过有限元仿真计算得到[16]。有限元软件仿真分析结果和理论计算结果对比,如图7所示。 图7 仿真分析和理论计算对比图 由图7可以看出,随着载荷的逐渐增大,仿真分析得到的量纲一接触面积与修正后理论计算得到的接触面积比例变化趋势基本一致,均呈线性增大。当载荷为100 MPa时,两者误差相对最大,为21.3%,随着载荷的不断增大,两者误差减小。当载荷增大到500 MPa时,误差最小为1.1%。误差产生的原因主要是理论分析接触面积的时候对模型作了简化处理,没有考虑实际微凸体在受压时,相近微凸体之间的相互作用对结果的影响等因素,同时有限元分析的时候,实体模型微凸体个数有限,只能在一定程度上反映整个微观粗糙表面接触情况。在一定误差范围内,仿真分析结果与修正后的理论结果相比于原单向分形表面接触模型更加吻合,证明修正后的单向粗糙分形接触模型更具有参考价值。 3.2实验对比 文献[17]通过实验和数学建模的方式对粗糙表面的真实接触面积与载荷之间的关系进行研究,研究对象为45钢,其弹性模量为210 GPa,屈服强度为355 MPa,泊松比为0.269,得到载荷与接触面积的关系曲线(两条)。将45钢的材料参数和分形参数代入到修正模型中,其中分形参数采用过盈配合模拟试件的分形参数,也得到一条载荷与接触面积的关系曲线,将三条曲线放在一起进行对比,如图8所示。 图8 实验和理论模型对比图 由图8可以看出,修正理论的载荷和量纲一接触面积关系与文献[17]提出的数学模型的计算结果和实验结果相近,证明本文提出的修正后的单向粗糙度分形接触理论模型具有参考意义。 (1)本文根据修正的M-B模型修正了具有单向粗糙度特征分形表面发生接触时微凸体接触宽度的分布。修正了原模型中当分形维数趋近于1时,总接触面积与最大微凸体接触面积的比值为1的不合理之处,进而推导出载荷与总接触面积的数学关系式,为具有单向粗糙度特征的分形表面发生接触时计算其真实接触面积提供了新的方法。 (2)比较原理论模型和修正后的理论模型,接触面积比例均随着载荷的增大而增大,两者近似成线性关系。修正模型中微凸体接触宽度的分布经过修正,当微凸体的接触宽度相同时,修正的模型中发生接触的微凸体数量较多,所以修正模型的接触面积比例在各载荷下均大于原模型的接触面积比例,当载荷较小(p=100 MPa)时,接触面积比例差值最小为7.73%,随着载荷的增大,差值随之增大;当载荷较大(p=500 MPa)时,接触面积比例差值最大为17.3%。 (3)通过有限元软件ANSYS仿真分析,仿真分析结果和理论推导结果基本吻合。采用相同的材料参数,修正模型的计算结果与文献[17]的数学模型和实验结果相差不大,说明针对本文涉及的过盈配合界面而言,修正后的单向粗糙度分形接触理论模型具有参考意义。 [1]张洪武,廖爱华,吴昌华.压气机过盈配合的弹塑性有摩擦接触的研究[J].工程力学,2007,24(1):185-192.Zhang Hongwu,Liao Aihua,Wu Changhua.Study on Elastoplastic Frictional Contact Problem in Interference Fits of Compressors[J].Engineering Mechanics,2007,24(1):185-192. [2]黄平,赖添茂.基于真实接触面积的摩擦模型[J].华南理工大学学报:自然科学版,2012,40(10):109-114. Huang Ping,Lai Tianmao. Friction Model Based on Real Contact Area[J].Journal of South China University of Technology:Natural Science Edition,2012,40(10):109-114. [3]刘宝庆.过盈联接摩擦系数的理论及试验研究[D].大连:大连理工大学,2008. [4]Majumdar A,Bhushan B.Fractal Model of Elastic-plastic Contact between Rough Surfaces[J]. Journal of Tribology (ASME),1991,113:1-11. [5]Majumdar A,Bhushan B.Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces[J].Journal of Tribology (ASME),1990,112:205-216. [6]Zhou G Y,Leu M C,Blackmore D.Fractal Geometry Prediction[J].Wear, 1993,170:1-14. [7]温淑花,张学良,武美先,等.结合面法向接触刚度分形模型建立与仿真[J] .农业机械学报,2009,40(11):197-200.Wen Shuhua,Zhang Xueliang,Wu Meixian,et al.Fractal Model and Simulation of Normal Contact Stiffness of Joint Interfaces and Its Simulation[J].Transactions of the Chinese Society for Agricultural Machinery,2009,40(11):197-200. [8]张长军,贺林.具有单向粗糙度表面接触的分形模型[J]. 西安公路交通大学学报,1998,18(4):105-109.Zhang Changjun,He Lin.Fractal Model of Contact between Rough Surface with One-dimensional Roughness[J].Journal of Xi’an Highway University,1998,18(4):103-107. [9]付秀娟.变速/变载条件下板料冲压成形性能及其变形机理研究[D].武汉:华中科技大学,2012. [10]Wang S,Komvopoulos K.A Fractal Theory of the Interfacial Temperature Distribution in the Slow Sliding Regime:Part Ⅰ—Elastic Contact and Heat Transfer Analysis[J]. ASME Journal of Tribology,1994,116(4):812-823. [11]O’Callaghan M,Cameron M A.Static Contact under Load between Nominally Flat Surfaces in Which Deformation is Purely Elastic[J].Wear,1976,36:76-97. [12]Francis H A.Application of Spherical Indentation Mechanics to Reversible an Irreversible Contact between Rough Surfaces[J].Wear,1977,45:221-269. [13]葛世荣,朱华.摩擦学的分形[M].北京:机械工业出版社,2005. [14]陈国安,朱真才,朱华.工程装备磨损研究[M].北京:兵器工业出版社,2003. [15]朱亚军.过盈配合温差拆解损伤问题的研究[D].合肥:合肥工业大学,2015. [16]陈东.再制造对象过盈配合的液压拆解问题研究[D].合肥:合肥工业大学,2013. [17]Kucharski S,Starzynski G.Study of Contact of Rough Surfaces Modeling and Experiment[J].Wear, 2014,311(S 1/2):167-179. (编辑袁兴玲) Study on Microscopic Contact Area in One-dimensional Fractal Interface of Interference Fits Shen JianYi LixiangZhou DanLiu GuangfuDu Xiaodong Hefei University of Technology, Hefei, 230009 Through the analyses of the surface profile based on the simulation fit between impeller and shaft, one-dimensional roughness feature of machined surface was obtained. Surface profile of vertical machining direction had obvious fractal characteristics. A theoretical contact model containing one-dimensional roughness feature and fractal characteristic was established based on modified M-B fractal contact model. And the calculation formulation of the real contact area under different normal contact loads was given. Combined with practical rough surfaces, a solid model with one-dimensional roughness feature and fractal characteristic was built to simulate and analysed by ANSYS. The results verified the calculation formulation. interference fit; microcosmic surface; contact model; fractal 2015-12-03 国家重点基础研究发展计划(973计划)资助项目(2011CB013400);国家自然科学基金资助项目(51405121) TH117.1 10.3969/j.issn.1004-132X.2016.19.002 沈健,男,1956年生。合肥工业大学机械工程学院教授。主要研究方向为机械设计与制造。易利祥,男,1991年生。合肥工业大学机械工程学院硕士研究生。周丹,女,1980年生。合肥工业大学机械工程学院副教授。刘光复,男,1945年生。合肥工业大学机械工程学院教授、博士研究生导师。杜晓东,男,1966年生。合肥工业大学材料科学与工程学院教授。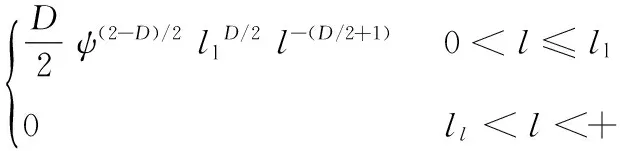
2 过盈配合界面形貌和接触分析


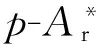


3 有限元软件仿真分析与实验对比


4 结论
