基于阻力测试的采煤机结构受力分析

陈洪月　张　坤　袁　智　毛　君

1.辽宁工程技术大学，阜新，123000 2.国家地方联合矿山液压技术与装备工程研究中心，阜新，123000 3.中国煤矿装备有限责任公司，北京，100011



基于阻力测试的采煤机结构受力分析

陈洪月1,2张坤1袁智3毛君1,2

1.辽宁工程技术大学，阜新，123000 2.国家地方联合矿山液压技术与装备工程研究中心，阜新，123000 3.中国煤矿装备有限责任公司，北京，100011

为了获取采煤机截割工作过程中行走支撑部件的载荷，采用经典力学理论建立了采煤机整机6阶模型，分析了模型求解时存在的不足，针对采煤机与刮板机间的四点支撑而引起的过约束问题，采用变形协调原理建立采煤机整机的受力模型，通过实验方法获取了左右驱动滚筒的载荷，并将其作为模型输入，采用逐步判别法进行数值求解。结果表明：左导向滑靴和平滑靴在Y向的受力比右侧小，两个导向滑靴的轴向受力相对较小且方向相反。最后通过实验对求解结果有效性进行了验证。

采煤机；变形协调原理；实验验证；整机受力分析

0　引言

由于采煤机工况恶劣、结构复杂，所以在实际生产中经常会发生采煤机的平滑靴严重磨损或导向滑靴、刮板输送机上的销排断裂的事故[1-3]，严重影响了煤矿井下的安全生产。因国内缺乏对采煤机整机详细的受力分析，各生产单位只能盲目地对导向滑靴或销排进行改进，导致采煤机与刮板输送机无法协调发展。相关理论研究方面，文献[4]建立了采煤机整机动力学模型，假设前导向支撑力为零，对采煤机的4个滑靴受力进行了分析。文献[5]假设前导向滑靴不受力，分析了不同工况下采煤机的载荷。文献[6]采用最小二乘法对各滑靴受力进行了逼近计算。文献[7]通过判断支反力的方向建立了不同的系数矩阵，再通过高斯约旦法对整机方程进行求解。文献[8]采用单次随机截割载荷模型和叠加法对整机进行了受力分析。文献[9]对滚筒采煤机整机进行载荷分析，计算了斜切状态下滚筒和滑靴处的载荷情况。

现有的研究成果中，多假设前导向滑靴受力为零以进行整机分析，并且缺乏相应的实验验证，导致理论计算结果与采煤机在实际工况下的受力存在较大的差异。采煤机工作过程中受其外部载荷的变化和现场工况的影响，其受力模型具有不确定性，本文先采用变形协调原理对采煤机整机受力分析模型进行降阶，再将整机模型的不确定性系数矩阵转换为明确性矩阵，并以实验获得的滚筒阻力作为输入载荷，采用逐步判别法对模型进行求解，最后通过实验对求解结果的有效性进行验证，研究结果为采煤机行走支撑部件的结构优化和寿命预测提供参考。

1　采煤机整机受力分析模型建立

如图1所示，令X轴为左右平滑靴的连线，采煤机行进方向为正；Y轴位于左右平滑靴的中心，向上为正；Z轴与滚筒轴线方向平行，面向采空侧为正。采煤机整机参数符号设定如下：行走牵引力为Ft、左滚筒水平载荷为Fgx1、竖直载荷为Fgy1、 轴向载荷为Fgz1、 扭矩为Mg1；右滚筒水平载荷为Fgx2、竖直载荷为Fgy2、轴向载荷为 Fgz2、扭矩为 Mg2；左右平滑靴的支撑力为Fhy1、Fhy2；左右导向滑靴竖直和轴向支撑力为Fdy1、Fdy2、Fdz1、Fdz2；刮板机的俯角为β，刮板机的侧倾角为α；左右摇臂的转角为α1、α2。

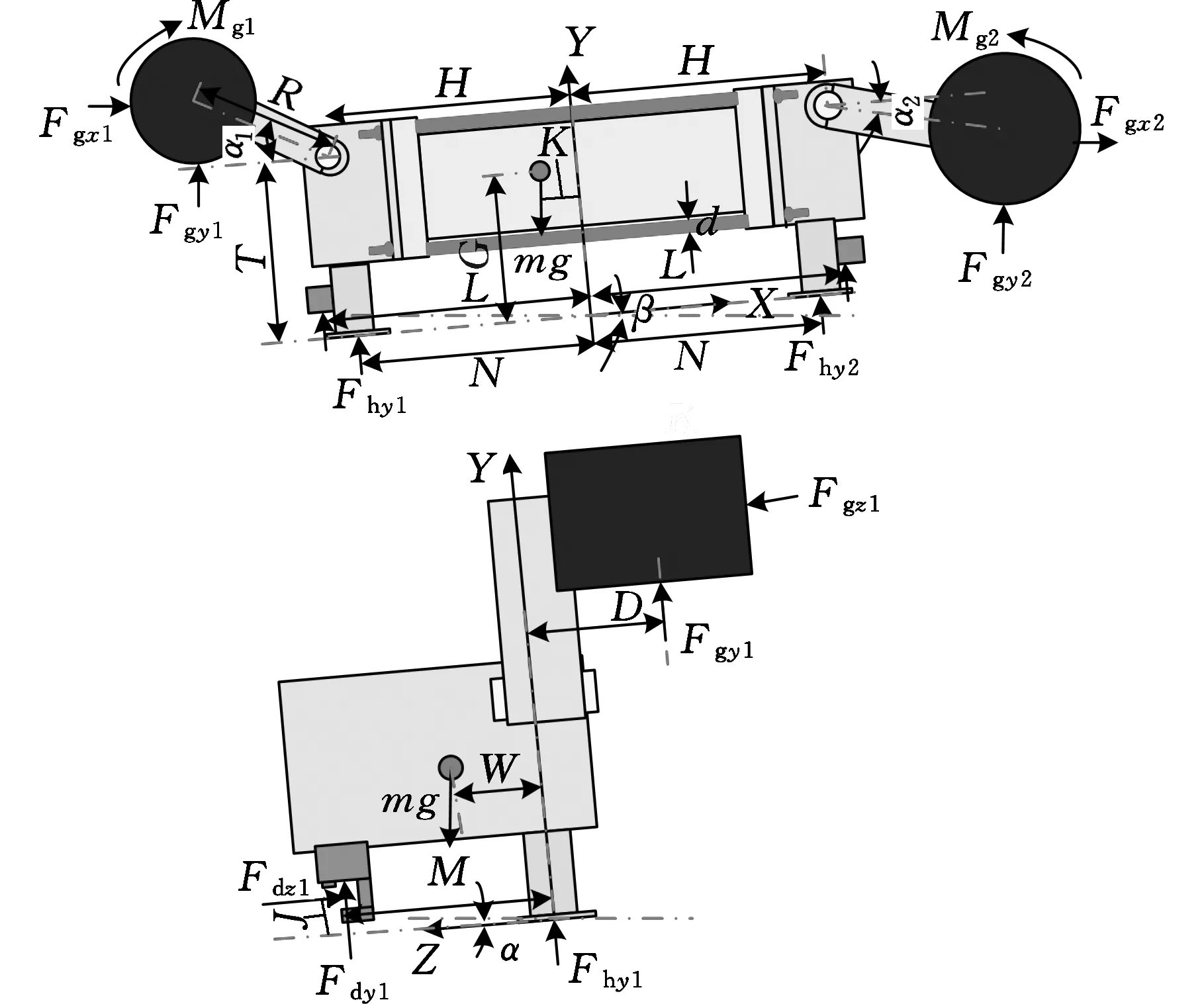
图1　采煤机受力分析图

结构尺寸参数如下：摇臂长度R=2.4 m，摇臂铰接点与机身底面的距离T=1.2 m，导向滑靴距整机中心L=2.9 m，平滑靴距整机中心N=3.1 m，平滑靴和导向滑靴在Z向距离M=1.2 m，平滑靴和导向滑靴在Y向距离J=0.25 m，截割臂的回转铰接点距机身中心H=1.2 m，整机重心距两个平滑靴连线的距离W=0.35 m，整机重心与整机中心间的距离K=0.3 m，整机重心与平滑靴底板间的距离G=0.98 m，滑靴与刮

板输送机中部槽的摩擦因数μ=0.2。

将Fdy1、Fdy2、Fdz1、Fdz2、Fhy1、Fhy2视为求解变量，采用理论力学受力分析方法，建立整机受力平衡方程。

由∑X=0可得

(|Fdy1|+|Fdy2|+Fhy1+Fhy2+|Fdz1|+|Fdz2|)μ=

(Fgx1+Fgx2-Ft)cosβ+mgsinβ

(1)

由∑Y=0 可得

Fdy1+Fdy2+Fhy1+Fhy2+(|Fdz1|+|Fdz2|)μ=

mgcosβcosα-(Fgy1+Fgy2)cosβ

(2)

由∑Z=0可得

(|Fdy1|+|Fdy2|+Fhy1+Fhy2)μ+Fdz1+Fdz2=

Fgz1+Fgz2+mgsinα

(3)

由∑MX=0可得

[Fdy1+Fdy2+(|Fdz1|+|Fdz2|)μ]M+

[Fdz1+Fdz2+(|Fdy1|+|Fdy2|)μ]J=

Wmgcosαcosβ+Fgz1(T+Rsinα1)+

Fgz2(T+Rsinα2)+(Fgy1+Fgy2)D

(4)

由∑MY=0可得

(|Fdy1|-|Fdy2|)μL+(Fdz1-Fdz2)L+

(Fhy1-Fhy2)μN=(Fgx2-Fgx1)D+

Fgz1(H+Rcosα1)-Fgz2(H+Rcosα2)+Wmgsinβ

(5)

由∑MZ=0可得

[Fdy1-Fdy2+(|Fdz1|-|Fdz2|)μ]L+

(Fhy1-Fhy2)N=-Fgy1(H+Rcosα1)+

Fgy2(H+Rcosα2)-Fgx1(T+Rcosα1)-

Fgx2(T+Rcosα2)+Kmgcosαcosβ+Gmgsinβ

(6)

整理后得

AX=B

(7)

B1=(Fgx1+Fgx2-Ft)cosβ+mgsinβ

B2=mgcosβcosα-(Fgy1+Fgy2)cosβ

B3=Fgz1+Fgz2+mgsinα

B4=Wmgcosαcosβ+Fgz1(T+Rsinα1)+

Fgz2(T+Rsinα2)+(Fgy1+Fgy2)D

B5=(Fgx2-Fgx1)D+Fgz1(H+Rcosα1)-

Fgz2(H+Rcosα2)+Wmgsinβ

B6=-Fgy1(H+Rcosα1)+Fgy2(H+Rcosα2)-Fgx1(T+Rcosα1)-Fgx2(T+Rcosα2)+Kmgcosαcosβ+Gmgsinβ

在系数矩阵A中，当Fdy1<0时i=-1,Fdy1≥0时i=1;当Fdy2<0时j=-1，Fdy2≥0时j=1;当Fdz1<0时m=-1,当Fdz1≥0时m=1;当Fdz2<0时n=-1，当Fdz2≥0时n=1。

由式(7)中的系数矩阵A可知：当方程变量解的正负号不同时，矩阵性质也有所改变，如所有求解变量全为正时，系数矩阵A的秩取5，说明其中一组系数是冗余的，而式(7)中未知变量个数为6，所以上述方程无解，但当Fdy1<0，而其余解均大于0时，系数矩阵的秩为6，方程存在唯一解，所以矩阵A存在不确定性。

再由图1可知：采煤机与刮板输送机间为四点支撑，属于过约束问题，所以采用经典理论力学方法很难对其进行求解，为此，本文引入小变形协调原理[10]，令采煤机平滑靴与刮板输送机中部槽间的接触弹性模量为Eh、接触面积为Ah，则接触刚度kh=EhAh，导向滑靴与中部槽上的销排接触弹性模量为Ed、接触面积为Ad，接触刚度kd=EdAd。

在采煤机的重心位置建立坐标系，如图2所示，令采煤机沿重心方向的位移为y，采煤机的俯角变形为θ、侧摆角变形为φ，则4个滑靴处的四

点支撑力可表示为

(8)

(9)

Fdy1=kd(y-aθ+dφ)

(10)

Fdy2=kd(y+bθ+dφ)

(11)

其中,a=N-K，b=N+K，c=M-W，d=W，e=L-K，f=L+K。

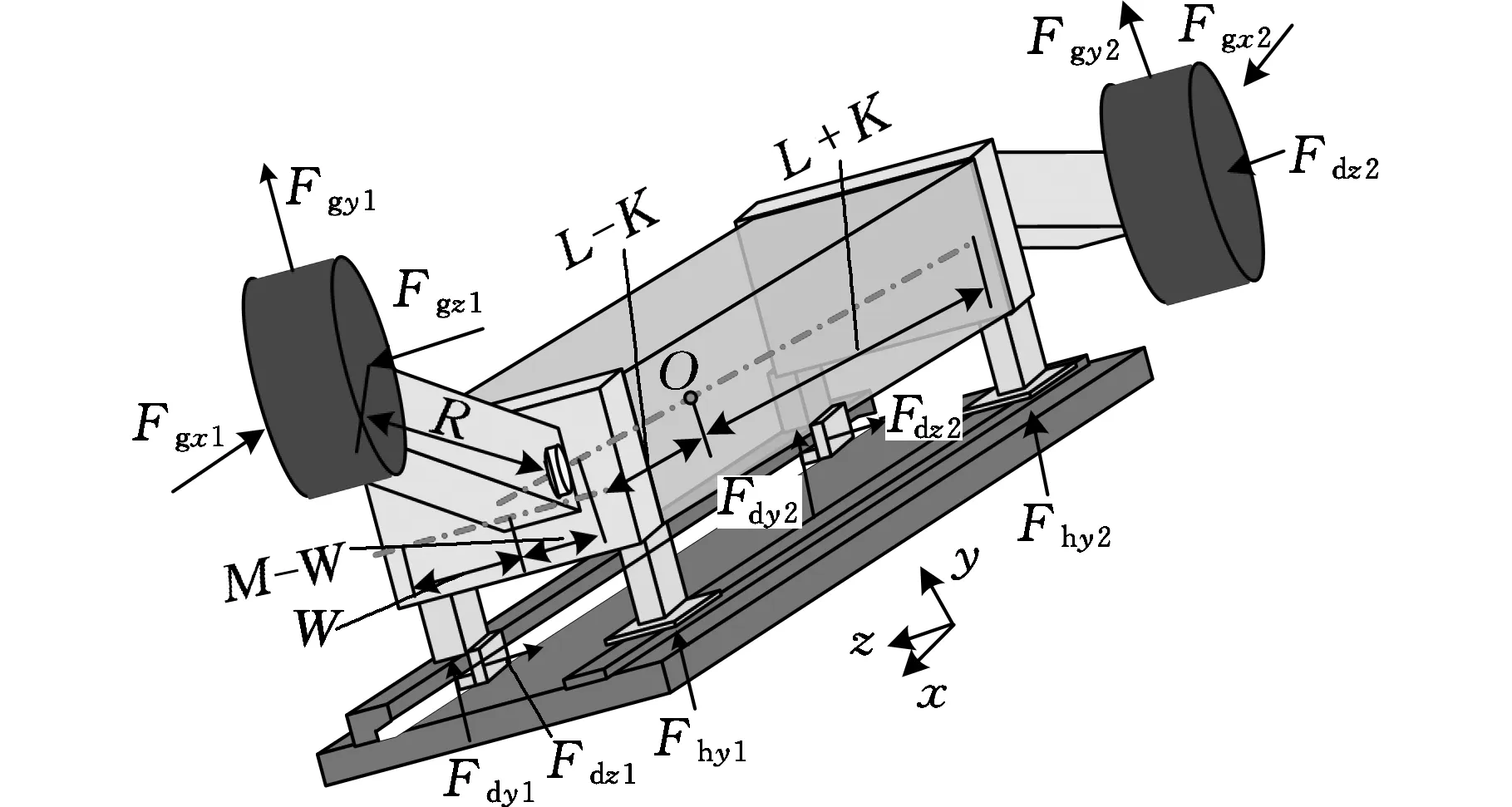
(a)整机受力分析

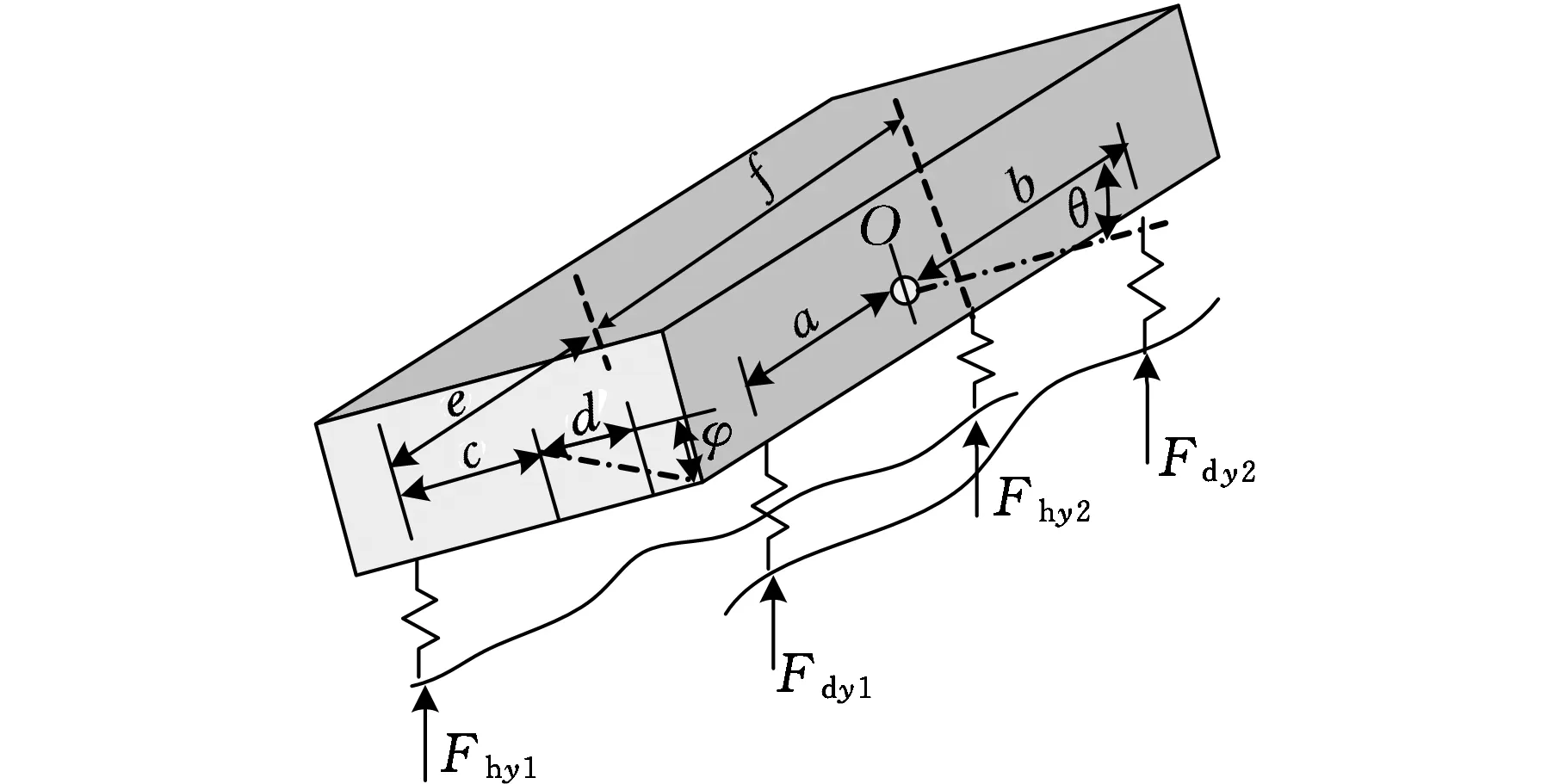
(b)滑靴四点支撑的小变形协调简图图2　采煤机三维受力分析

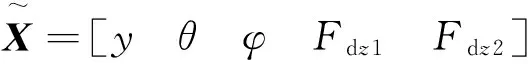
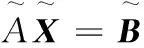
(12)

p=w+vq=i+jr=w-vs=i-j

式中,w、v、i、j、m、n均为状态系数。

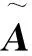
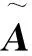
2　采煤机整机力学模型求解与实验验证

2.1滚筒载荷获取

采煤机滚筒载荷的确定是整机受力模型求解的前提，本文采用实验方法来获取滚筒载荷，实验地点为中煤集团国家能源煤矿采掘机械装备研发(实验)中心，实验中所截割煤壁普氏硬度f0=3，煤壁高3 m，长70 m。实验过程中，截齿的工作阻力通过安装在齿座上的应变片进行测量，应变片共有三组，分别粘贴在齿座轴径的安装孔内，三组应变片分别用于测量截齿截割过程中的侧向阻力、牵引阻力、截割阻力，齿座的下端通过销轴固定在滚筒的方形孔内，如图3a所示。在滚筒的边缘安装有测量滚筒旋转位置的传感器，以便于确定滚筒上截齿的旋转角度，如图3b所示。三向力传感器所采集的信号通过滚筒后端的无线发射模块发射到数据接收中心，截齿三向力传感器及发送模块的安装如图3c所示。平滑靴销轴传感器与无线发射模块安装在一起，安装位置如图3d所示。实验中的数据采集系统为Beedate无线采集系统，刮板机的俯角为β=0°，刮板机的侧倾角为α=0°，采煤机滚筒截割转速为35.2 r/min，截深为500 mm，采煤机行走速度为2 m/min，实验现场如图4所示。

(a)齿座示意图　　　　　(b)滚筒位置传感器

(c)截齿传感器安装　　　(d)滑靴销轴传感器图3　传感器安装

图4　实验现场

令Xi、Yi、Zi分别为滚筒上第i个参与截割的截齿的侧向阻力、牵引阻力、截割阻力；Fgx、Fgy、Fgz、Mg分别为滚筒在行走方向的阻力载荷、竖直方向的阻力载荷、轴向的阻力载荷、截割扭矩，根据文献[11]有

其中,Nc为滚筒上参与截割的截齿总数，Rg为滚筒的半径，φi为第i个截齿与滚筒竖直方向的夹角。因实验煤层厚度为3 m，滚筒直径为1.8 m，根据采煤机的结构参数可知：工作时左右摇臂的摆角α1=20°、α2=-18°，又因每个滚筒上安装36个截齿，所以工作过程中左滚筒参与截割的截齿数量为18个，右侧滚筒参与截割的齿数为12个，分别截取截齿载荷的10组数据，将其代入式(13)后得到的滚筒载荷，如图5、图6所示，左侧滚筒因其参与截割的齿数大于右侧，故其载荷要大一些，其三方向的阻力载荷和阻力扭矩均值为：Fgx1=137 kN，Fgy1=173 kN，Fgz1=33.5 kN，Mg1=48.7 kN·m。右滚筒：Fgx2=99.3 kN，Fgy2=131 kN，Fgz2=22.6 kN，Mg2=22.2 kN·m。

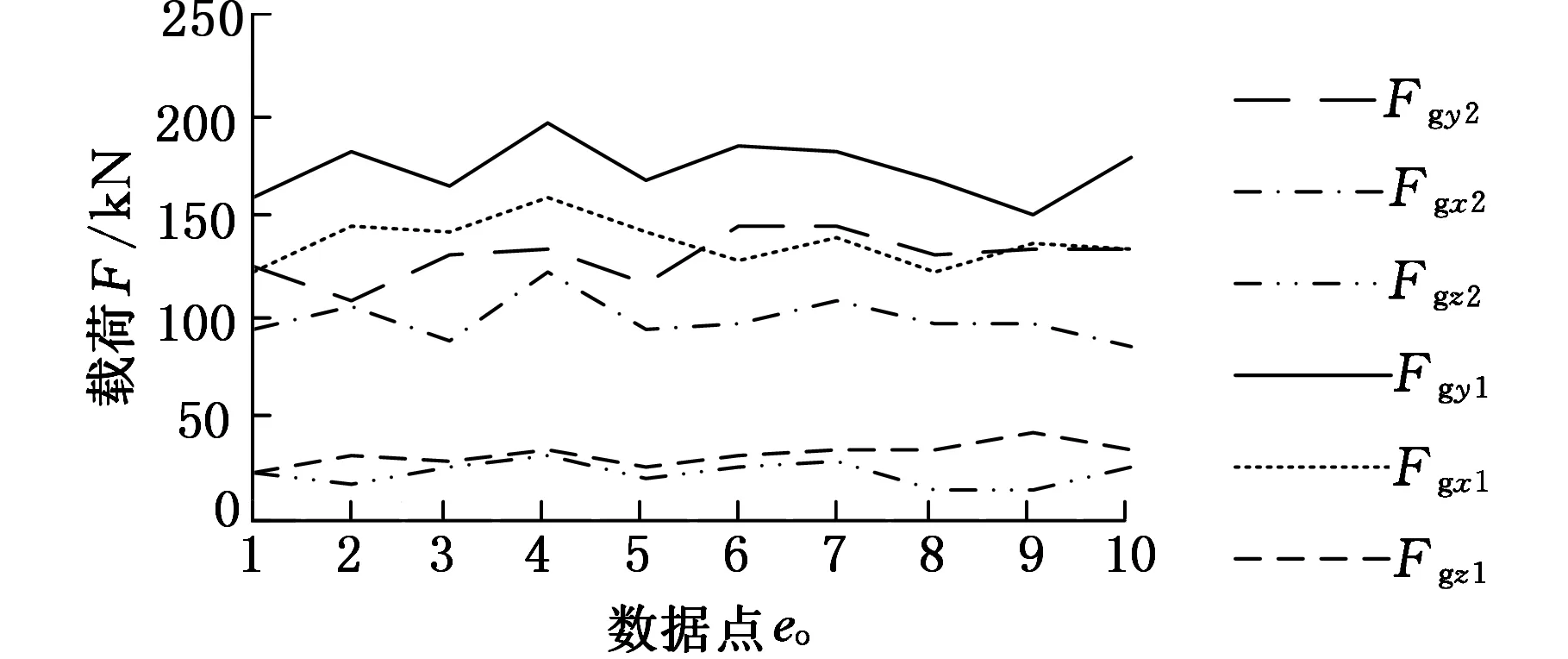
图5　左右滚筒三向力载荷

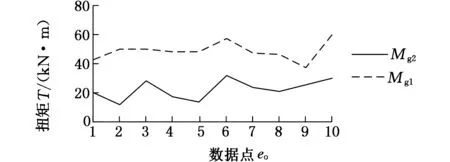
图6　左右滚筒截割扭矩载荷

2.2滑靴受力求解与验证

由于式(12)中的系数矩阵具有不确定性，故为了获得精确解，本文将不确定性系数矩阵分解为64组明确的系数矩阵，从而形成64组明确的方程[12-13]，因式(12)的唯一解只能来自64种可能发生的条件中的一种，所以采用逐步判别的方法对其进行求解，求解过程如图7所示。

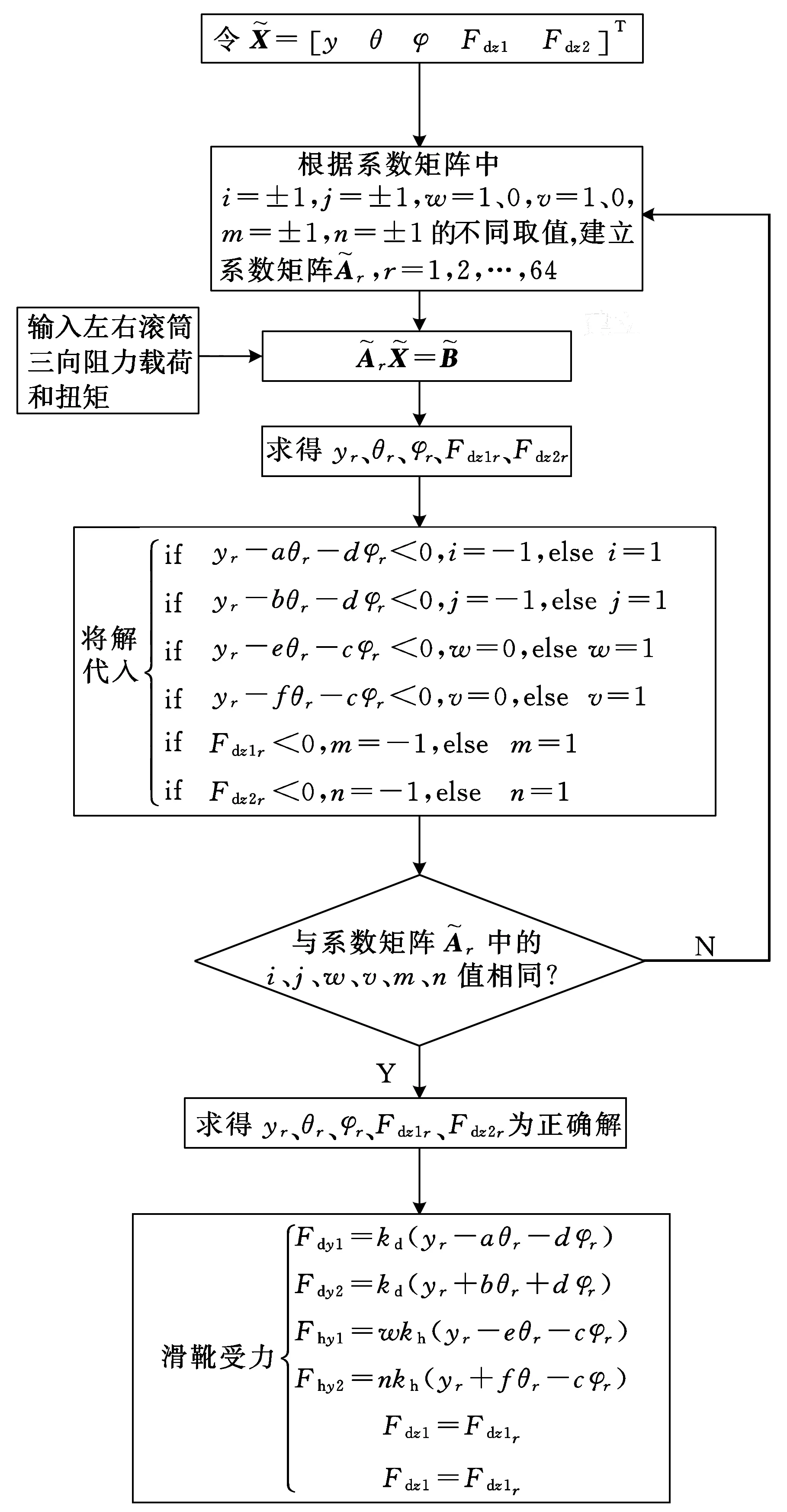
图7　方程求解方法

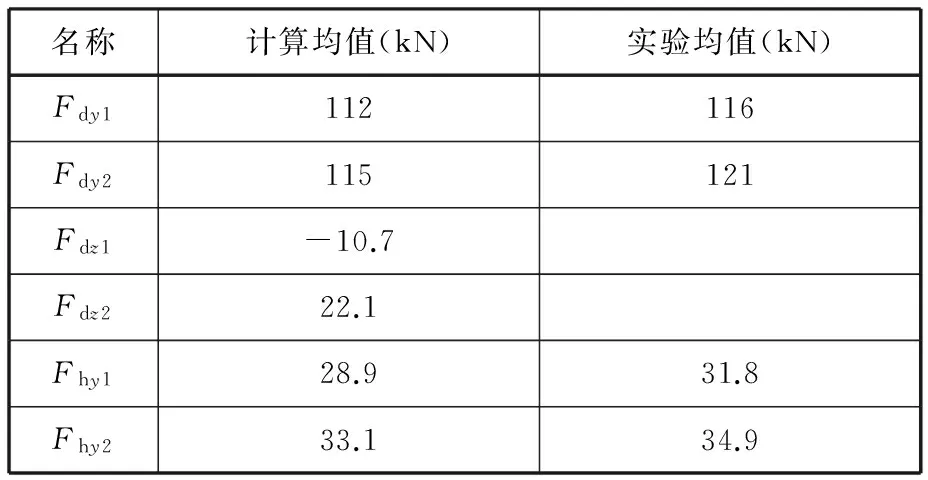
方程组的求解结果和实际测量结果如图8所示，均值如表1所示。由图8a、图8b可知：采煤机工作过程中，左导向滑靴和平滑靴在Y向的受力比右侧小，这是因为采煤机工作过程中，左侧滚筒上的阻力载荷Fgx1、Fgy1、Mg1及右侧滚筒上阻力载荷Fgx2使机身左侧产生一种向上抬起的趋势，故左导向滑靴和平滑靴在竖直方向受力相对较小。由图8c可知：两个导向滑靴的轴向受力很小，但左导向滑靴受力为负，说明左导向滑靴受到了指向煤壁侧的轴向力，对比数值分析结果和实验结果可知：两者间的变化趋势较为一致，但实验值要稍大于计算值，引起误差的主要原因是刮板输送机相邻的中部槽及销排的连接处存在高度差，当采煤机行走经过连接位置时，会产生一定的冲击，从而导致滑靴实际受力增大。

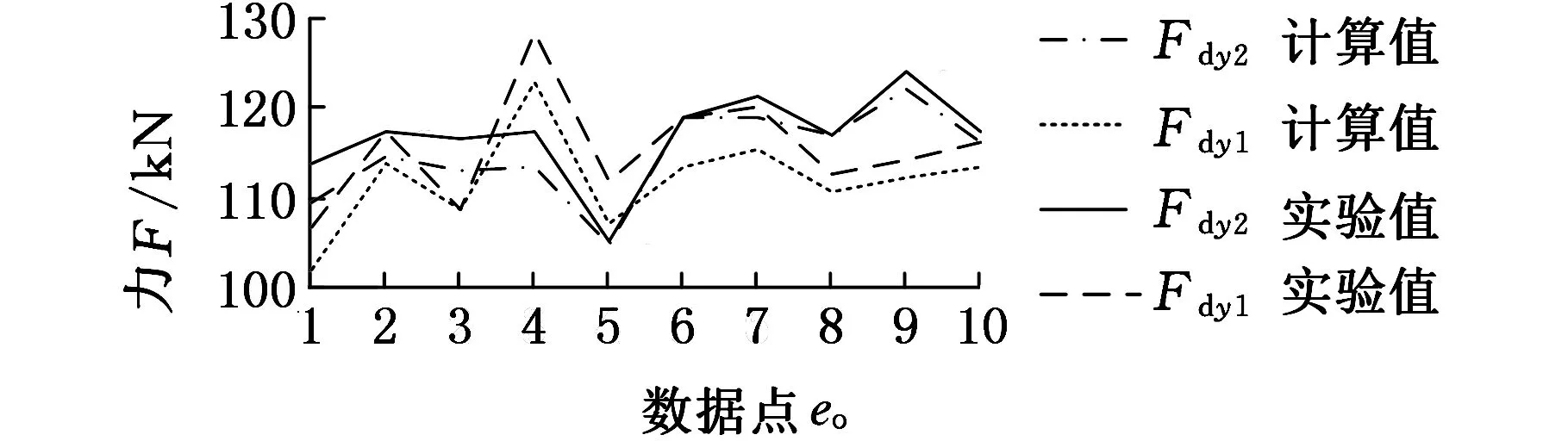
(a)导向滑靴竖直方向载荷

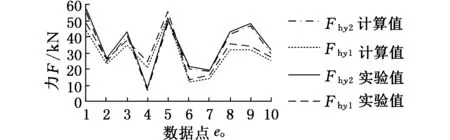
(b)平滑靴竖直方向载荷

(c)导向滑靴轴向方向载荷图8　滑靴受力理论计算值与实际测量值

名称计算均值(kN)实验均值(kN)Fdy1112116Fdy2115121Fdz1-10.7Fdz222.1Fhy128.931.8Fhy233.134.9

3　结论

(1)采用变形协调原理建立了采煤机整机静力学方程，将采煤机整机6阶静力学模型转换为5阶，解决了原采煤机静力学模型无法求得精确解的问题。

(2)采用实验方法获取了采煤机截割工程中前后滚筒的截割阻力，并将其作为模型的输入，对采煤机静力学模型进行了数值求解，得到了截割工况下采煤机平滑靴和导向滑靴的受力值。分析结果表明：左导向滑靴和平滑靴在Y向的受力比右侧小，左右导向滑靴支撑力均值分别为112 kN、115 kN，左右平滑靴支撑力均值分别为28.9 kN、33.1 kN，两个导向滑靴的轴向受力相对较小但方向相反，左边受到了指向煤壁侧的轴向力并将求解结果与实验测量值进行了对比，验证了模型的正确性。

[1]龚平,周建强,吕元和. MG375型采煤机导向滑靴损坏的原因分析[J].煤炭科技,2006(4):9-10.

Gong Ping, Zhou Jianqiang, Lü Yuanhe. Analysis of the Damage Reason of Guide Foot of MG375-type Shearer[J].Coal Science & Technology Magazine,2006(4):9-10.

[2]郎国军,苑雪涛,庹文敏,等. 采煤机行走轮断齿现象分析[J]. 煤矿机电,2010,(3):34-36.

Lang Guojun,Yuan Xuetao,Tuo Wenmin, et al. Analysis of Tooth-break Fault on Shearer’s Walking Wheel[J]. Mechanical and Electrical, 2010(3):34-36.

[3]赵永生,杨怀东,赵庆禹. 大倾角煤层综采工作面采煤机可靠性分析[J]. 煤矿机械, 2013,34(8):103-105.

Zhao Yongsheng, Yang Huaidong, Zhao Qingyu. Analysis on Reliability of Shearer on High Inclined Fully Mechanized Working Face[J]. Coal Mine Machinery 2013,34(8):103-105.

[4]张炳军,刘春生,林海鹏. 采煤机整机受力分析[J].东北煤炭技术,1999,5(10):40-42.

Zhang Binjun, Liu Chunsheng, Lin Haipeng. Analysis of Force for Shearer[J]. Northeast Coal Technology,1999,5(10):40-42.

[5]杨丽伟,葛红兵,胡俊,等.多工况下的采煤机载荷分析[J].煤矿机械,2011,32(1):91-93.

Yang Liwei,Ge Hongbing,Hu Jun,et al. Analysis of Force for Shearer in Various Conditions[J].Coal Mine Machinery, 2011,32(1):91-93.

[6]刘春生, 田操. 采煤机整机力学模型的最小二乘解算方法[J].辽宁工程技术大学学报:自然科学版,2015,34(4):505-510.

Liu Chunsheng, Tian Cao.Solution of Mechanical Model of Whole Shearer Based on Least Square Principle[J].Journal of Liaoning Technical University:Natural Science,2015,34(4):505-510.

[7]刘春生,戴淑芝. 双滚筒式采煤机整机力学模型与解算方法[J]. 黑龙江科技学院学报,2012,22(1):33-38.

Liu Chunsheng, Dai Shuzhi. Mechanical Modeling of Whole Double-drum Shearer and Its Solution[J]. Journal of Heilongjiang Institute of Science & Technology, 2012,22(1):33-38.

[8]刘春生,李德根,戴淑芝. 随机载荷对双滚筒采煤机整机力学特性的影响[J]. 煤矿机电,2012(6):45-48.

Liu Chunsheng,Li Degen,Dai Shuzhi. Influence of Random Load on Mechanical Properties of Double-drum Shearer[J]. Mechanical and Electrical, 2012(6):45-48.

[9]毛君,姜鹏,谢苗. 斜切状态下滚筒采煤机液压拉杠力学分析与寿命预测[J]. 工程设计学报,2015,22(1):95-100.

Mao Jun, Jiang Peng, Xie Miao. ForceAnalysis and Life Prediction of Hydraulic Rod on Drum Shear under the Condition of Oblique Cutting[J]. Chinese Journal of Engineering Design, 2015,22(1): 95-100.

[10]单祖辉.材料力学[M].北京:高等教育出版社,2010.

[11]刘春生. 滚筒式采煤机理论设计基础[M]. 徐州:中国矿业大学出版社,2003.

[12]王磊.n阶线性模糊微分方程的结构元解法[J]. 数学的实践与认识,2010,42(10):168-174.

Wang Lei. Fuzzy Structuring Element Method for nth-order fuzzyDifferential Equation[J]. Mathematics in Practice and Theory,2010,42(10):168-174.

[13]Chen Minghao, Li Daohua, Xue Xiaoping. Periodic Problems of First Order Uncertain Dynamical Systems[J]. Fuzzy Sets and Systems, 2010, 162 (1)：67-78.

(编辑袁兴玲)

Mechanics Analyses of Shearers Based on Resistance Tests

Chen Hongyue1,2Zhang Kun1Yuan Zhi3Mao Jun1,2

1.Liaoning Technical University, Fuxin, Liaoning,123000 2.National and Local Combined Mining Technology and Equipment Engineering Research Center,Fuxin, Liaoning, 123000 3.China National Coal Mining Equipment Co., Ltd., Beijing, 100011

To obtain the loads on the walking support unit of a shearer during the cutting processes, a 6-order model was established by applying the theories of the classical mechanics, and the disadvantages of the model were analyzed. Aiming at the over constrained problems caused by the 4 supporting points between the shearer and the scraper machine, the mechanics model for the entire shearer was proposed by using the deformation compatible equation. The loads on the left driving roller and the right driving roller were achieved by the experiments, and the loads were input into the model. The model was numerically solved by employing the successive discrimination method. The solving results show that the forces inYdirection on the left guiding boot and the left smooth boot are as smaller than that on the right sides, the axial forces on the two guiding boots are small but the directions of them are opposite. The solving results were validated by the experiments, and the results show that the model is effective.

shearer：deformation compatibility principle; experimental verification; mechanics analyses of whole machine

2015-11-30

国家能源研发(实验)中心重大项目(2010-215);辽宁省教育厅创新团队资助项目(LT2013009);国家自然科学基金资助项目(51404132)

TD421

10.3969/j.issn.1004-132X.2016.19.015

陈洪月，男，1982年生。辽宁工程技术大学机械工程学院副教授、博士研究生导师。主要研究方向为机械系统动态特性。张坤，男，1990年生。辽宁工程技术大学机械工程学院硕士研究生。袁智，男，1972年生。中国煤矿装备有限责任公司高级工程师。毛君，男，1960年生。辽宁工程技术大学机械工程学院教授、博士研究生导师。