基于干扰观测器的龙门机床双驱系统的同步控制

李　萍　朱国力　龚时华　岳　岚

华中科技大学，武汉，430074



基于干扰观测器的龙门机床双驱系统的同步控制

李萍朱国力龚时华岳岚

华中科技大学，武汉，430074

根据动梁式龙门机床双驱动系统的结构特点及运动特性，基于拉格朗日方程，建立了龙门机床两轴之间的机械耦合模型，结合传动系统动态模型和伺服系统三闭环控制结构，得到了龙门机床双驱动系统模型；为了降低非对称结构和偏心负载等干扰对同步性能的影响，提高系统的抗干扰性，提出了一种基于干扰观测器(DOB)的双驱动系统同步控制方法；最后进行了仿真分析，仿真结果表明，通过干扰观测器对干扰进行补偿后，龙门机床双驱动系统的同步性能得到了明显的提高。

双驱动系统；机械耦合模型；同步控制；干扰观测器

0　引言

龙门式双驱动结构同步控制的研究越来越受到国内外学者们的重视。Iván等[1]针对双驱龙门式工业机器人，提出了基于模型解耦的同步控制方法，该方法通过模型简化和坐标变换，采用前馈与反馈控制实现了模型的解耦控制；程瑶等[2]从质量、阻尼和刚度等基本因素出发，分析了动梁式龙门机床同步系统的不同步误差的影响因素，得到了这些因素对同步性能的影响规律；何王勇[3]以双滚珠丝杠同步驱动为研究对象，利用有限元结合集中参数的方法，由拉格朗日方程推导出双滚珠丝杠同步驱动轴的动力学模型，为同步控制提供了参考模型；Lin等[4]针对龙门式双驱定位平台，提出了基于三自由度动态模型的非奇异终端滑模智能控制方法，该方法综合使用模糊逻辑理论和递归神经网络方法以及非奇异滑模变结构控制，解决了双驱系统非线性和参数不确定性的控制问题；陆世荣等[5]提出了双伺服电机同步运行的最优控制策略，该控制方法基于线性二次型调节器的性能指标设计了最优控制器，并采用转矩扰动观测器进行前馈补偿以克服突加负载对系统的影响，实现了系统良好的同步性能和抗干扰性。以上学者都只注重双驱动同步控制算法的研究，对双驱动系统模型尤其是双轴耦合模型没有作详细分析，没有考虑负载的移动以及强干扰力对同步精度的影响。

本文以ZK5540A龙门数控铣床为例，根据动梁式龙门数控机床的结构特点及运动特性，将龙门机床双驱动系统的龙门机构的运动分为平移和旋转两部分，然后根据拉格朗日方程，建立双轴机械耦合模型。按照设定点协调控制方法[6]建立双驱动系统模型。为降低干扰对双驱动系统同步性能的影响，设计干扰观测器，对干扰进行补偿，提高系统的抗干扰性。最后，通过仿真验证了本文所提出的同步控制方法的可行性。

1　双驱动系统模型

龙门数控机床双驱动系统(图1)由电气伺服系统和机械伺服系统组成。机械伺服系统包括龙门机构和传动装置，两运动轴通过龙门机构实现耦合；电气伺服系统包括驱动电机、反馈装置和控制器。驱动系统采用三相永磁同步电机，具体模型参照文献[7-8]，本文主要是对龙门机床双轴耦合部分和传动装置进行建模。

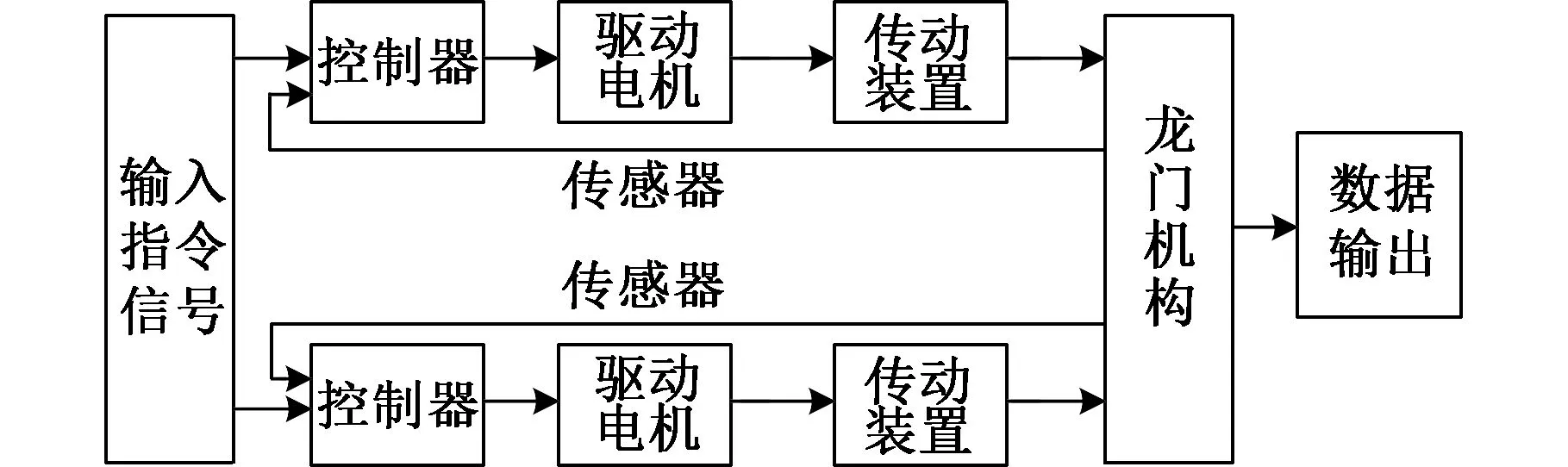
图1　龙门机床双驱动系统示意图

1.1龙门机床的机械描述

一个典型的龙门机构如图2所示。双驱动系统中两个伺服电机通过传动系统驱动受静压导轨约束的滑座1和滑座2，滑座通过螺栓连接带动龙门立柱和横梁，横梁上面安装可沿Y方向滑动的滑枕和刀架，刀架承受切削载荷。理想情况下两轴位移X1=X2，但是由于滑枕和刀架的Y方向移动，会使龙门机构的重心偏离几何中心，这样就会造成两伺服轴动态性能的差异，加上强切削力的干扰作用，使龙门机构倾斜产生同步误差。

图2　动梁式龙门机床示意图

1.2双轴机械耦合模型

图3所示为三自由度动梁式龙门机床双驱动系统模型。在这个模型中可以用两种坐标系来描述龙门机床的运动情况：一种是由各驱动机构的位置组成，即(X1,X2,Y)；另一种等效坐标系是通过龙门机床的中心位置、倾斜角以及负载的位置来描述，即(X,θ,Y)。两坐标系的关系为

(1)

(2)

式中，Lb为龙门机构两滑座之间的跨距。

图3　三自由度动梁式龙门机床双轴机械耦合模型

龙门机床双驱动系统的同步误差由龙门机构倾斜产生，为了更好地描述两轴之间非对称结构和偏心负载对于同步精度的影响，本文采用(X,θ,Y)坐标系来建立三自由度动梁式龙门机床双轴耦合的动力学模型。

图3中，mb、mh、m1和m2分别是龙门横梁、滑枕和滑座1、滑座2的质量；Cg1、Cg2和Cgy分别是滑座1、滑座2和滑枕的黏性摩擦因数；Cc1、Cc2和Ccy分别是滑座1、滑座2和滑枕的库仑摩擦力；Kbn和Cbn分别是龙门滑座与导轨之间等效油膜刚度系数和阻尼系数(n=1,2,3,4)；ls为单侧两弹簧阻尼器之间的等效距离；F1、F2和Fy为驱动力，FL为切削负载。

考虑到龙门横梁和立柱、滑座之间的固定连接，其总质量用Mb表示，即Mb=m1+m2+mb。相对于几何中心点的转动惯量用Ib表示，即

(3)

根据拉格朗日方程建立龙门机构动态模型的微分方程。为此，需要定义与其动态性相关的能量表达式，包括动能T、弹性势能V和瑞利耗散函数D[1]，其表达式如下：

(4)

(5)

(6)

对于龙门动梁式模型的三自由度(X,θ,Y)坐标系，其对应的广义力定义为

(7)

联合式(4)～式(7)，含有耗散函数的拉格朗日方程可以表示为

(8)

其中，广义坐标qj=(X,θ,Y)；广义力Fj=(FX,Fθ,FY)；L=T-V。

龙门机构耦合模型的微分方程可以表示如下：

(9)

式中，M、C、K分别为质量矩阵、阻尼系数矩阵和刚度系数矩阵；H为Coriolis和向心力矩阵；q=(X,θ,Y)T为广义自由度向量；F=(FX,Fθ,FY)T为广义力向量。

1.3模型的简化

实际上，龙门机构由于不同步而产生的旋转角θ非常小(θ<0.0001rad)，有cosθ≈1，sinθ≈0，式(9)中质量矩阵M中的M12、M21、M13和M31可近似为

(10)

类似地，Coriolis和向心力矩阵H中的所有元素都可以忽略不计，即H≈0。最后得到耦合模型的运动微分方程为

(11)

式中，Ms、Cs、Ks分别为简化模型的质量矩阵、阻力系数矩阵和刚度系数矩阵；Fs为简化模型的广义力向量；qs为简化模型的广义自由度向量。

式(1)中各矩阵的形式如下：

(12)

(13)

(14)

(15)

(16)

对于Y轴，其独立的动力学微分方程为

(17)

1.4传动系统动态模型

本文所研究的双驱动系统是用两平行的伺服电动机通过减速器+齿轮齿条传动装置来驱动龙门机构的，齿条固定在滑座上，滑座通过螺栓连接带动龙门横梁运动，龙门双驱系统中单轴传动装置示意图见图4。

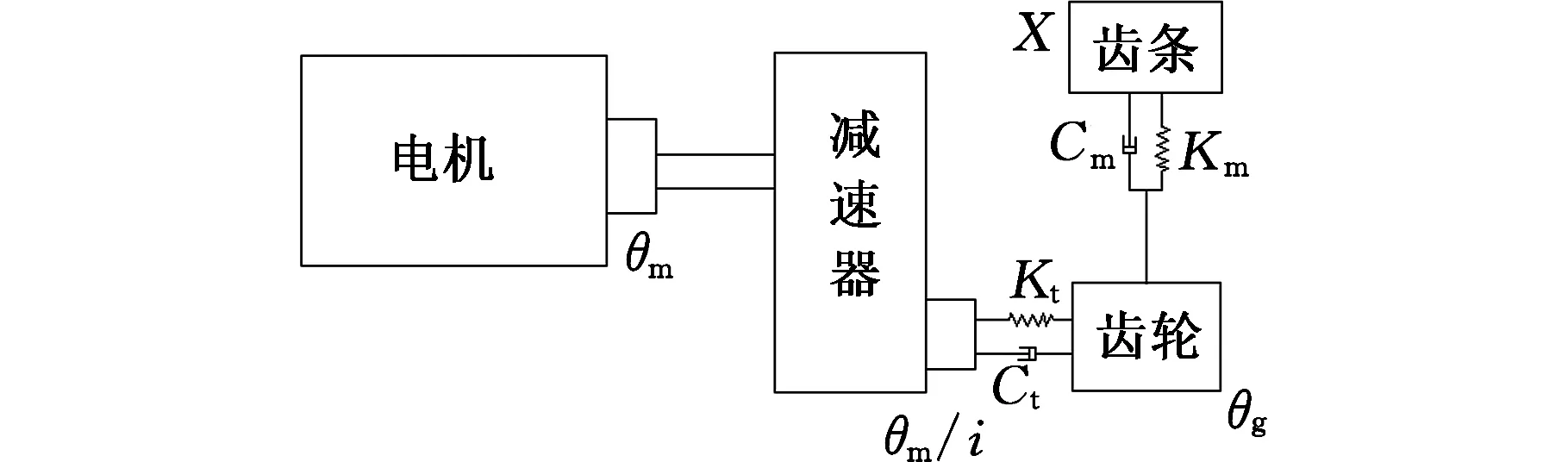
图4　单轴传动系统示意图

齿轮传动系统的动力学微分方程如下[9]：

(18)

(19)

(20)

式中，Tmj、Fj分别为传动系统的输入扭矩和输出力；θmj、θgj分别为电机轴和齿轮轴的角位移；Xj为齿条的直线位移；i为减速器传动比；Rgj为齿轮齿条传动半径；Jmj、Jcj、Jgj分别为电机、减速器和齿轮的转动惯量；Ctj、Cmj分别为扭转等效阻尼和齿轮啮合阻尼系数；Ktj、Kmj分别为扭转等效刚度和齿轮啮合刚度系数；btj、bgj分别为电机轴和齿轮轴黏性摩擦系数；下标j=1,2,代表第1、第2伺服驱动系统。

2　双驱动系统同步控制

龙门数控机床双轴驱动系统的基本控制方法是设定点协调控制，每根轴都有独立的伺服控制回路，共同执行相同的指令信号，通过各自的传动系统共同驱动龙门机构运动。两伺服驱动的伺服环路要尽可能地使实际轨迹与指令轨迹保持一致，实现同步。双驱动系统同步控制结构如图5所示。

图5　基于干扰观测器的龙门机床双驱系统同步控制框图

2.1单轴伺服系统控制参数整定

本文在实现龙门轴的PID控制参数整定时，先按照单轴伺服系统控制参数整定的方法进行参数整定[7-8，10]，然后用具有相同控制参数的两伺服系统共同驱动龙门机构，实现同步控制。

单轴伺服系统三环PID控制参数按照典型“Ⅰ型系统”和“Ⅱ型系统”整定电流环和速度环PI控制参数。位置环采用P调节器[10]。本文使用MATLABPIDTuner工具确定位置环增益，在保证位置环不超调的条件下将增益系数调到最大。

2.2干扰观测器设计

两伺服系统的控制参数和机械结构参数都存在差异，尤其是非对称质量和负载的存在，会严重地影响两轴的同步性。如果把两轴之间参数差异和非对称质量产生的惯性力以及非对称负载当作干扰，然后设计干扰观测器，对两轴都进行干扰补偿，可以有效地降低两轴同步误差，提高同步精度。

图6　干扰观测器原理图

低通滤波器Q(s)除消除高频噪声和保证逆模型的物理实现外，还对DOB的稳定性有直接影响，是DOB设计的关键。目前最流行的设计方法为Lee[11]提出的公式,即

(21)

式中，τ为截止频率的倒数；N为分母阶数；M为分子阶数；N-M为相对阶。

DOB设计的要点是确定Q(s)的阶次、相对阶和带宽[12-13]。分母阶次越大，系统越稳定，然而，分母阶次增大会导致Q(s)相位滞后，消弱对干扰的补偿作用；增大分子阶次会减小相位滞后，提高抗干扰能力，但是会破坏系统稳定；相对阶应不小于名义模型的传递函数的相对阶；截止频率要考虑鲁棒性和干扰抑制能力的折中，Q(s)的频带越宽，扰动抑制的能力会越强，但系统的鲁棒性会变差。

由于龙门机床的双轴驱动控制系统模型非常复杂，故通过公式推导的方式获得系统的名义模型Pn(s)非常困难。本文首先基于系统辨识理论[14]，采用最小二乘法，根据采集的驱动力矩信号Tm和轴位移信号X数据，对被控对象的模型进行辨识，然后以该辨识模型作为系统的名义模型来设计干扰观测器。

3　仿真验证

3.1控制系统参数整定

由表1中的驱动电机参数和表2龙门机床的机械参数，按照文献[7-8，10]的参数整定方法，可以得到伺服系统三环控制器参数，如表3所示。

整定后的系统性能如表4所示，从结果看，数控龙门机床位置伺服系统实现了位置无超调，并且响应快、稳定性良好，单轴的跟踪误差约为0.1mm。速度设定值与实际值以及跟踪误差曲线如图7、图8所示。

上述参数整定方法是基于模型的调节方法，在实际控制参数调节过程中，由于无法准确地获得控制系统模型，并且还要考虑摩擦阻尼的影响，以及两轴耦合作用的影响，实际中参数的整定需要在此基础上进行微调，以便获得更好的控制性能。

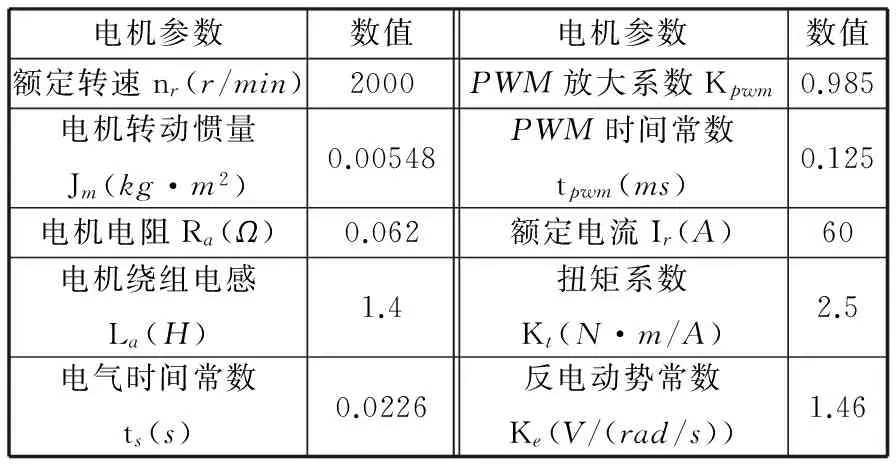
表1　伺服电机参数

表2　龙门机床机械参数

表3　三环PID控制参数整定值

表4　整定后系统性能表

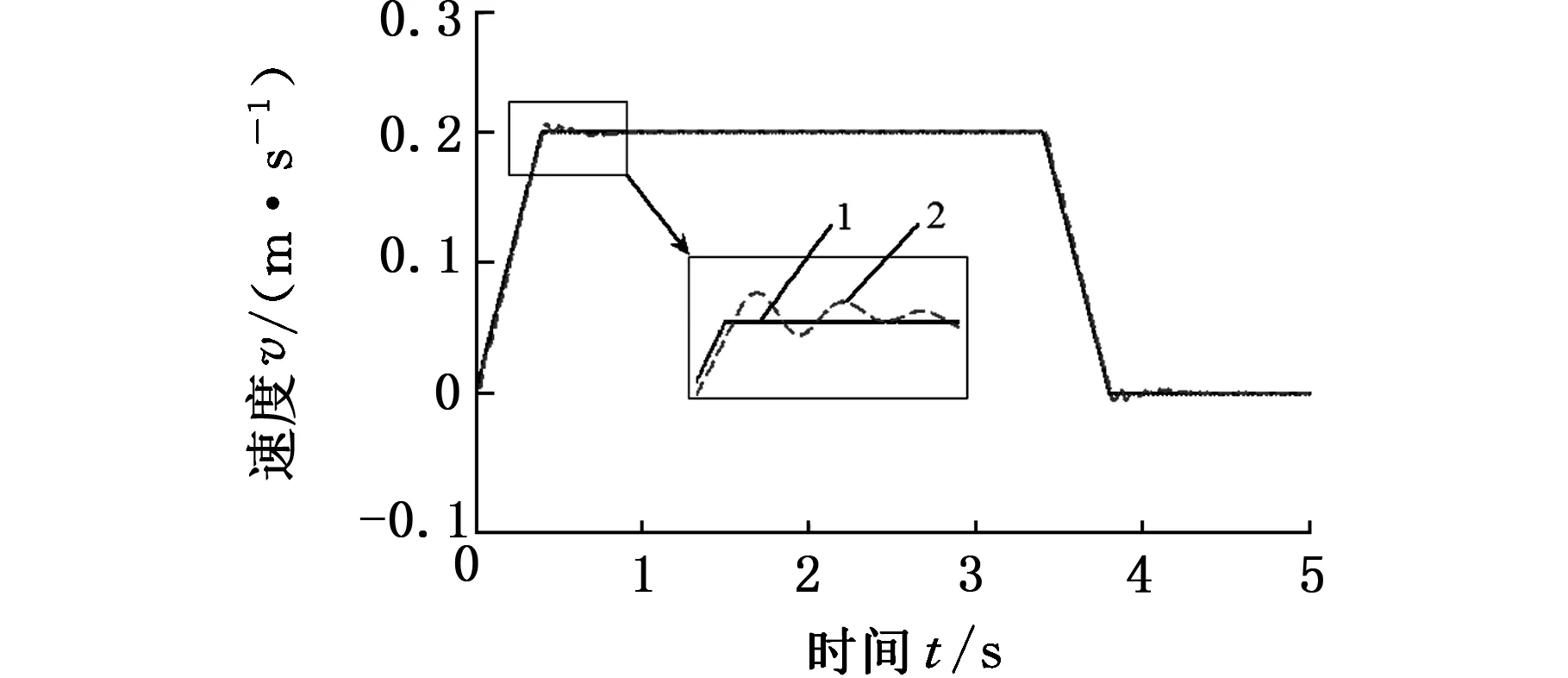
1.速度设定值　2.速度实际值图7　速度设定值与实际值曲线

图8　跟踪误差曲线

3.2干扰补偿

首先对单轴X1的伺服系统进行模型辨识，通过移动滑枕，使得Y=0，即有M12=M21≈0，选用特征多项式为F(s)=s12⊕s11⊕s8⊕s6⊕1的M序列速度指令为激励信号，以电机驱动力矩T1为输入信号，X1的轴位移为输出信号进行模型辨识，辨识模型为

(22)

数据拟合度为96.13%，FPE值为0.0102，系统实际测量的输出数据和辨识模型仿真数据对比如图9所示。

1.实际测量输出数据　2.辨识模型仿真数据图9　实际模型的输出数据和辨识模型输出数据对比

以辨识出来的模型式(22)作为两轴的名义模型Pn(s)，综合考虑控制精度、抗干扰性和系统稳定性，设计低通滤波器为Q31(s)型滤波器，时间常数τ=0.001s，可得

(23)

3～6s添加一矩形干扰力FL=12 kN，滑枕位移Y=2 m，横梁跨度Lb=4.8 m，折算到两滑座的负载FL1=11 kN，FL2=1 kN，干扰实际值和观测值如图10所示，干扰未补偿和补偿的同步误差如图11所示。

图10　干扰实际值和观测值

1.未补偿的同步误差曲线　2.补偿后的同步误差曲线图11　补偿和未补偿的两轴同步误差曲线

由图11可以看出，使用干扰观测器并对干扰力进行补偿，最大同步误差由0.28mm减小到0.13mm，恢复时间由0.75s缩短到0.25s，双驱动系统同步控制的干扰抑制性能在加入干扰观测器后得到了显著的提高。由图12可以看出，低通滤波器Q(s)时间常数越低，分母阶数越高，同步误差峰值越小，系统的抗干扰能力越好，增加分子阶数可以改善相位特性。

(a)不同时间常数

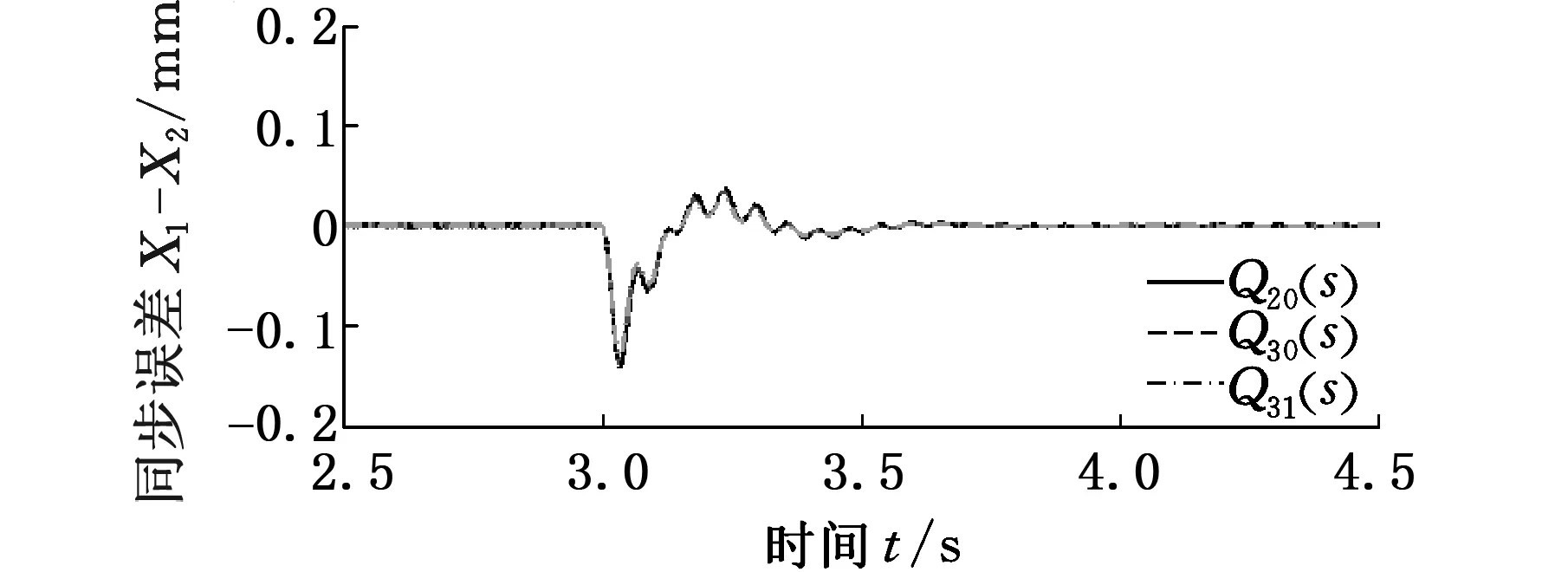
(b)不同阶数图12　不同时间常数τ和不同阶数Q(s)的同步误差曲线

4　结语

本文根据动梁式龙门机床的结构特点和运动特性，基于拉格朗日方程，对双驱动系统同步运动产生同步误差的原因及机理进行了建模研究，建立了动梁式龙门机构机械耦合模型，并结合两轴传动系统模型和三环伺服驱动系统模型，建立了龙门机床双驱动系统的同步控制模型。采用广泛应用的PID调节器进行控制，并对三环控制参数进行整定。为了降低非对称负载和强切削干扰对同步性能的影响，设计了基于辨识模型的干扰观测器，对干扰进行补偿，提高了系统的抗干扰性。最后借助于MATLAB/Simulink仿真平台，验证了所采用同步控制方法的可行性，双驱动系统抗干扰性能在使用干扰观测器对干扰进行补偿后得到显著提高。

[1]IvánG-H,XavierK.Model-basedDecouplingControlMethodforDual-driveGantryStages:aCasestudywithExperimentalValidations[J].ControlEngineeringPractice, 2013， 21(3):298-307.

[2]程瑶，梁滔，赵万华. 动梁式龙门机床双轴同步系统的模型建立及不同步误差分析[J]. 机械工程学报, 2013, 49(13):174-182.ChengYao,LiangTao,ZhaoWanhua.Non-synchronousErrorandModelingofDual-driveSysteminGantry-typeMachineToolswithTravellingBridge[J].JournalofMechanicalEngineering, 2013, 49(13):174-182.

[3]何王勇. 数控机床双轴同步控制技术研究[D]. 武汉：华中科技大学, 2011.

[4]LinFJ,ChouPH,ChenCS,etal.Three-degree-of-freedomDynamicModel-basedIntelligentNonsingularTerminalSlidingModeControlforaGantryPositionStage[J].IEEETransactionsonFuzzySystems, 2012, 20(5): 971-985.

[5]陆世荣, 吴向东, 李谦，等. 双伺服电机同步运行的最优控制[J]. 微特电机, 2015, 43(3): 63-65.

LuShirong，WuXiangdong，LiQian，etal.OptimalControlofDoubleServoMotorSynchro-runningSystem[J].SmallandSpecialElectricalMachines, 2015, 43(3): 63-65.

[6]陈国强 李崇兴，黄苏南. 精密运动控制：设计与实现[M]. 北京: 机械工业出版社, 2011.

[7]李润方，王建军. 齿轮系统动力学[M]. 北京:科学出版社, 1997.

[8]孙宇, 王志文, 孔凡莉，等. 交流伺服系统设计指南[M]. 北京:机械工业出版社, 2013.

[9]施丽婷, 黄筱调, 杨勇. 数控交流伺服系统三环整定及应用[J]. 南京工业大学学报(自然科学版), 2006, 28(4):36-40.

ShiLiting,HuangXiaodiao,YangYong.ParameterTuningandApplicationoftheThreeLoopsinaNCServoSystem[J].JournalofNanjingUniversityofTechnology(NatureScienceEdition), 2006, 28(4):36-40.

[10]潘月斗, 李擎, 李华德. 电力拖动自动控制系统[M]. 北京:机械工业出版社, 2014.

[11]LeeHS.RobustDigitalTrackingControllersforHigh-speedHigh-accuracyPositioningSystems[D].California:UniversityofCaliforniaBerkeley,1994.

[12]MizuochiM,TsujiT,OhnishiK.ImprovementofDisturbanceSuppressionBasedonDisturbanceObserver[C]//InternationalWorkshoponAdvancedMotionControl.Istanbul, 2006, 229-234.

[13]WangCC,TomizukaM.DesignofRobustlyStableDisturbanceObserversBasedonClosedLoopConsiderationUsingH∞InfinityOptimizationandItsApplicationstoMotionControlSystems[C]// 2004AmericanControlConference(AAC).Berkeley,CA, 2004:3764-3769.

[14]萧德云，方崇智. 系统辨识理论及应用[M]. 北京：清华大学出版社，2014.

(编辑袁兴玲)

程学院博士研究生。主要研究方向为机电一体化、数控系统伺服控制。朱国力，男，1966年生。华中科技大学机械科学与工程学院教授、博士研究生导师。龚时华，男，1968年生。华中科技大学机械科学与工程学院教授、博士研究生导师。岳岚，女，1992年生。华中科技大学机械科学与工程学院硕士研究生。

Synchronous Control of Dual-drive System in Gantry-type Machine Tools Based on Disturbance Observer

Li PingZhu GuoliGong ShihuaYue Lan

Huazhong University of Science and Technology, Wuhan，430074

According to the structure and motion characteristics of the double drive system in CNC gantry-type machine tools with moving beams, a mechanical coupling dynamic model of double drive system in the gantry-type machine tools was established based on Lagrange’s equation. Combined with the dynamic model of transmission system and the three closed loop control structure of servo system, the double drive system model of gantry machine was obtained. In order to reduce the effects of asymmetric structure and eccentric load disturbance on the synchronization accuracy and improve the anti-interference of the system, a dual drive system synchronization control method was proposed based on DOB. Finally, the simulation analyses were carried on. The simulation results show that the synchronization performance of double drive system to improve in gantry-type machine tools is obviously improved after the disturbance compensation by disturbance observer.

dual-drive system; mechanical coupling model; synchronous control; disturbance observer(DOB)

2015-12-07

国家科技重大专项(2013ZX04013-011)

TH39；TP273

10.3969/j.issn.1004-132X.2016.19.012

李萍，男，1989年生。华中科技大学机械科学与工