几类Lorenz型高维混沌系统的动力学行为研究

张 光 云

(重庆工商大学 数学与统计学院， 重庆 400067)



几类Lorenz型高维混沌系统的动力学行为研究

张 光 云

(重庆工商大学 数学与统计学院， 重庆 400067)

混沌系统在各个领域中都有着广泛的研究，其中混沌系统的最终有界性在混沌系统的同步和控制等领域中有着重要的应用；采用理论分析和计算机模拟相结合的方法，研究了几类高维混沌模型的非线性动力学行为，得到了类混沌模型的吸引域，从而展示了混沌系统的丰富的动力学特性并且用matlab给出了相应的计算机模拟。

混沌模型；混沌控制；吸引域；稳定性

1　数学模型

从自然科学的角度来说，混沌的理论可以追溯到大约1900年庞加莱关于三体问题的研究，发现它的运动轨迹是非周期的，并且永远不递增，也不趋于固定点。1963 年,美国气象学家E.Lorenz在研究大气对流时，首次给出了著名的Lorenz混沌方程。Lorenz混沌系统作为第一个混沌系统模型有着重要的理论研究意义和工程应用价值。一般认为混沌具有一些主要特征，如确定性、有界性、对初值的极端敏感性、长期的不可预测性、正的最大lyapunov 指数、遍历性等。在Lorenz混沌方程基础上Chen混沌系统，Lü 混沌系统，超混沌Lorenz系统等及其在工程中的应用问题得到了一系列的研究[1-10]。混沌在生物工程、力学工程、电子工程、化学工程、信息工程、计算机工程、应用数学和实验物理等领域都有着广泛的应用。其次，混沌还有很多潜在的应用价值。由于很多混沌系统与Lorenz系统不是拓扑等价的，从而它们的混沌动力学特性是未知的，据作者所知现有文献对高维混沌系统的动力学研究方面的文章还是比较的少，而且由于高维混沌系统自身结构的复杂性和特殊性因而在保密通信方面有更好的潜在应用，因此有必要对新高维混沌系统的动力学特性进行研究。

一个新混沌模型为[11-12]

(1)

其中参数R≠0为系统(1)的雷诺参数。当R=35.6,R=58.64,R=74.44时，系统(1)轨线在x1x5x7空间中的相图, 分别如图1—图3所示。

图1　R=35.6时,系统(1)的轨线的相图Fig.1　When R=35.6, phase portraits of trajectory of system (1)

图2　R=58.64时,系统(1)的轨线的相图Fig.2　When R=58.64, phase portraits of trajectory of system (1)

图3　R=74.44时,系统(1)的轨线的相图Fig.3　When R=74.44, phase portraits of trajectory of system (1)

一个新九模类Lorenz混沌模型为[13]

其中参数r≠0为系统(3)的雷诺参数。

一个新七阶微分混沌模型为[14]

(3)

其中参数Re≠0为系统(3)的雷诺参数。当Re=100,系统轨线的相图，见图4。

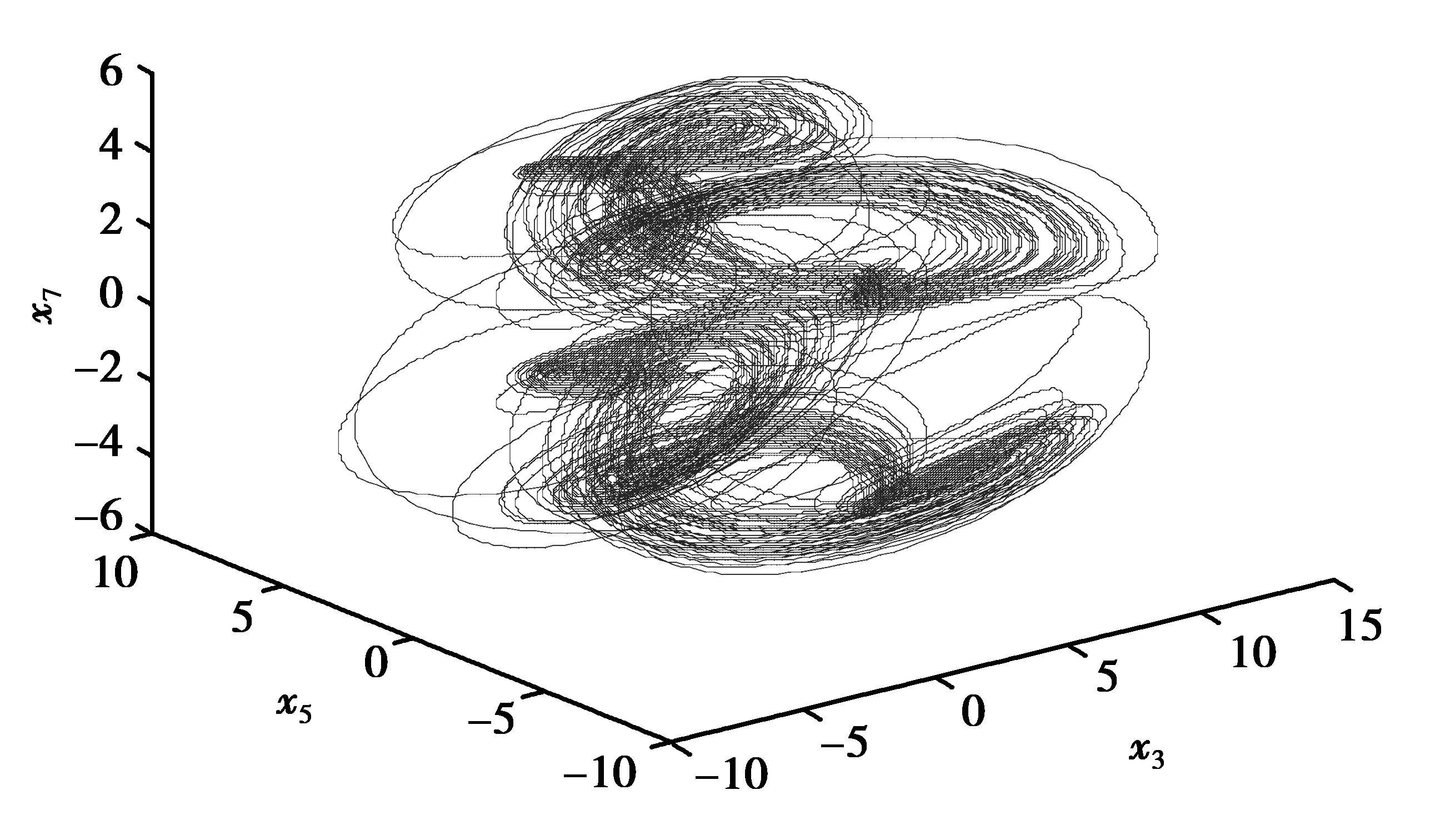
图4　系统(3)的轨线相图Fig.4　When Re=100,phase portraits of trajectory of system (3)

2　主要数学结果

定理1对任意的R≠0, 令

当V(X(t))≥L0,V(X0)>L0(t≥t0)时，对于系统(1)的正半轨线，有指数估计式：

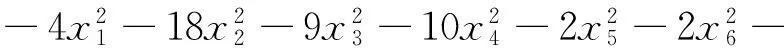
两边积分有V(X(t))-L0≤[V(X0)-L0]e-2(t-t0).

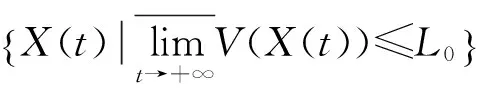
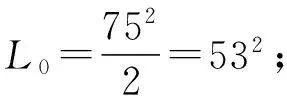
图5　系统(1)的轨线最终进入Ω之内Fig.5　Trajectory entering into Ω of system (1)

定理2对任意的r≠0, 令

当V(X(t))≥M0,V(X0)>M0(t≥t0)时，对于系统(2)的正半轨线，有指数估计式：

用ZMD-2型电子密度计，采用排水法测量烧结试样的烧结密度；用Leica DM4000型显微镜，对烧结试样的横截面进行孔隙度测试；用DM400M型金相显微镜，对烧结试样进行显微组织分析；用HR-150A型洛氏硬度计，测量试样的硬度(HRB)．

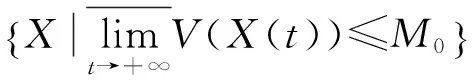
两边积分有V(X(t))-M0≤[V(X0)-M0]e-2(t-t0)。

定理3对任意的Re≠0, 令

当V(X(t))≥M0,V(X0)>M0(t≥t0)时，对于系统(3)的正半轨线，有指数估计式：

两边积分有V(X(t))-M0≤[V(X0)-M0]e-2(t-t0)

3　结　论

鉴于混沌系统模型的重要理论研究和应用价值，首先给出了几类混沌系统的数学模型，然后从数学理论上研究了该混沌模型的吸引集，最后给出了相应的数值仿真。所得结果具有一定的理论和实际意义。

[1] 袁红,张付臣,李小武.关于Hopf分岔中向量函数泰勒公式中算子系数表示的评注[J].重庆工商大学学报(自然科学版),2012,29(10): 6-10

YUAN H,ZHANG F C,LI X W.Remarks on Operator Coefficient in Taylor Formula for Vector Function of Hopf Bifurcation[J].J Chongqing Technology Business University(Natural Science Edition),2012,29(10): 6-10

[2] 龙健生,舒永录,杨洪亮.一个多维混沌系统的最终有界集和正向不变集及其在同步之中的应用[J].重庆工商大学学报(自然科学版),2011,28(6): 551-557

LONG J S,SHU Y L,YANG H L.The Ultimate Bound Set and Positively Invariant Set for a Multi-dimension Chaotic System and its Application in Chaos Synchronization[J].J Chongqing Technol and Business University(Ntural Science Edition),2011,28(6): 551-557

[3] 陈福利.忆阻混沌系统的同步[J].重庆工商大学学报(自然科学版),2015,32(8): 24-27

CHEN F L.Synchronization of the Memristor-based Chaotic System[J].J Chongqing Technol and Business University(Ntural Science Edition),2015,32(8): 24-27

[4] 王志强,王书玲,吴然超.时滞Lorenz-like系统的Hopf分岔研究[J].重庆工商大学学报(自然科学版),2015,32(2): 11-15

WANG Z Q,WAGN S L,WU R C.Research on Hopf Bifurcation of Lorenz-like Delay System[J].J Chongqing Technol and Business University(Ntural Science Edition),2015,32(2): 11-15

[5] 胡玉婷,李东,张兴鹏.参数未知的分数阶混沌系统的自适应追踪控制[J].重庆工商大学学报(自然科学版),2015,32(3): 1-7

HU Y T,LI D,ZHANG X P.Adaptive Tracking Control of Fractional Order Chaotic Systems with Unknown Parameters[J].J Chongqing Technol and Business University(Ntural Science Edition),2015,32(3): 1-7

[6] He X,YU J Z,HUANG T W.Neural Networks for Solving Nash Equilibrium Problem in Application of Multiuser Power Control [J].Neural Networks,2014,57(9): 73-78

[7] 毛北行,孟晓玲,卜春霞.离散非线性系统的混沌同步问题[J].重庆师范大学学报(自然科学版),2014,31(2):40-42

MAO B X,MENG X L,PU C X.Chaos Synchronization Problem of Discrete Nonlinear System[J].Journal of Chongqing Normal University (Natural Science Edition),2014,31(2):40-42

[8] 张学兵.一个新混沌系统的分析与控制[J].重庆师范大学学报(自然科学版),2012,29(2): 55-59

ZHANG X B.Analysis and Control of a New Chaotic System[J].Journal of Chongqing Normal University (Natural Science Edition),2012,29(2): 55-59

[9] 张春涛,刘学飞,应宏,等.空气质量的混沌动力学分析[J].西南大学学报(自然科学版),2012,34(11):47-51

ZHANG C T,LIU X F,XIANG H,et al.Chaotic Dynamic Analysis of Air Quality[J].Journal of Southwest University (Natural Science Edition),2012,34(11):47-51

[10] 杨磊,舒永录,何兴.Qi系统的脉冲控制与同步[J].西南师范大学学报(自然科学版),2012,37(7):37-45

YANG L,SHU Y L,HE X.On Impulsive Control and Synchronization of Qi System[J].Journal of Southwest China Normal University (Natural Science Edition),2012,37(7):37-45

[11] 高焱，王贺元.二维不可压缩Navier-Stokes 方程的七模类Lorenz 方程组的动力学行为及其数值模拟[J].辽宁工业大学学报(自然科学版),2008,28(4):257-262

GAO Y,WANG H Y.Simulation of Dynamic Characteristics and Numerical Value on 2D-lincompressible Navier-Stokes Equation with Their Seven Modes Lorenz Equations[J].Journal of Liaoning University of Technology (Natural Science Edition),2008,28(4):257-262

[12] SHILNIKOV A,NICOLIS G,NICOLIS C.Bifurcation and Predictability Analysis of a Low Order Atmospheric Circulation Model[J].International Journal of Bifurcation and Chaos,1995(5):1701-1711．

[13] 高焱.九模类Lorenz系统的动力学行为及其数值模拟[J].应用数学学报,2014,37(3): 507 -515

GAO Y.The Dynamical Behavior and The Numerical Simulation of a Nine-mode Lorenz Equations[J].Acta Mathematicae Applicatae Sinica,2014,37(3): 507-515

[14] WANG H Y,CUI Y,HUANG M.A New Seven-modes Truncation of the Plane Incompressible Navier-Stokes Equations[J].Chinese Quarterly Journal of Mathematics,2012,27(1): 11-17

责任编辑：田静

Dynamical Analysis of Several Lorenz High-Dimensional Chaotic Models

ZHANG Guang-yun

(School of Mathematics and Stutistics, Chongqing Technology and Business University,Chongqing 400067, China)

Chaotic systems have been widely studied in various engineering fields. The ultimate bound of chaotic system has important applications in chaos synchronization and control field. The dynamics of several kinds of chaotic models are studied in this paper by theoretical analysis and computer simulation. The trapping regions of chaotic models are obtained. It shows that three kinds of chaotic models have rich dynamic characteristics. The corresponding computer simulation is given by Matlab.

chaotic model; chaotic control; trapping region; stability

10.16055/j.issn.1672-058X.2016.0005.003

2016-03-02；

2016-04-05.

张光云(1983-)，女,山东临沂人,助教,硕士,从事外国语言学及应用语言学、常微分方程研究.

O241.84

A

1672-058X(2016)05-0011-05