多涡卷混沌吸引子个数连续变化的同步方法*

黄　沄， 赵卫峰

(重庆邮电大学 资产管理处，重庆 400065)



多涡卷混沌吸引子个数连续变化的同步方法*

黄沄， 赵卫峰

(重庆邮电大学 资产管理处，重庆 400065)

提出了一种多涡卷混沌吸引子个数连续变化的同步方法；基于Lyapunov稳定性原理，设计了一个同步控制器；同步控制器能在保持不变的情况下，使吸引子个数连续变化的多涡卷混沌系统保持同步；以Colpitts网格多涡卷超混沌系统和超混沌Lorenz系统的同步为例，进行了数值仿真研究，仿真结果表明所设计的同步控制器的有效性。

混沌；多涡卷混沌系统；超混沌Lorenz系统;同步

由于多涡卷混沌系统具有十分复杂的动力行为，因此把多涡卷混沌系统应用于保密通信中能增加保密通信的安全性。而混沌的同步又是实现混沌保密通信的基础，因此对多涡卷混沌系统的同步[1-11]研究已成为目前的研究热点。如文献[7]研究了一种基于滞环非线性的多涡卷混沌系统的广义同步；文献[8]利用滑模控制实现了多涡卷混沌系统的同步；文献[9]研究了多方向多涡卷混沌系统的广义同步；文献[10]利用单变量反馈控制法实现了多涡卷混沌系统的同步。然而，文献所报道的多涡卷混沌系统的同步都是在吸引子个数固定情况下实现的，而对多涡卷混沌吸引子个数连续变化的同步，目前还鲜见报道。由于多涡卷混沌系统在吸引子个数连续变化下产生的混沌信号较固定下产生的混沌信号更复杂，因此研究多涡卷混沌吸引子个数连续变化的同步具有重要意义。

巧妙地应用符号函数，设计了一种不含多涡卷混沌系统的非线性函数的同步控制器。由于多涡卷混沌系统的吸引子个数的变化意味着其非线性函数的变化，因此在多涡卷混沌系统的吸引子个数连续变化时，同步控制器能保持不变，并且能使吸引子个数连续变化的多涡卷混沌系统与其响应系统仍保持同步状态。

1　问题描述

考虑如下两个混沌系统：

(1)

(2)

多涡卷混沌系统(1)为驱动系统，系统(2)为响应系统。x,y∈Rn是n维状态向量，矩阵A，A1，B，B1∈Rn×n，且B和B1为正定对角阵。f(x),g(y)∈Rn是系统的非线性部分。U(x,y)为同步控制器。

定义系统(1)和系统(2)的同步误差为

(3)

式(3)中，ei=xi-yi,i= 1, 2,…,n。

U(x,y)=(A-A1)y-B1g(y)+NBsgn(e)+ke

(4)

证明定义Lyapunov函数

(5)

为了叙述方便，定义正定对角阵B = diag (b1,b2,…,bn)，bi> 0,i= 1, 2, …,n。

与交流配网不同，多端柔性直流配电网内带有大量电力电子设备，系统阻抗小短路电流传播速度快、幅值大；存在多电源环网运行方式，直流线路存在T型接法且长度较短，使得故障选线定位较为困难。鉴于此，需要研究适用于多端直流配电网的保护配置策略。

对V求导得

=eT[Ae-ke+Bf(x)-KBsgn(e)

=eT(A-k)e+eT[Bf(x)-KBsgn(e)]

=eT(A-k)e+eT[Bf(x)-KBsgn(e)]

综上，由于系统(1)的涡卷吸引子个数由非线性函数f(x)决定。而同步控制器(4)不含f(x)，因此同步控制(4)能在保持不变的情况下，使涡卷个数连续变化的多涡卷混沌系统(1)与系统(2)保持同步。

2　数值仿真

选取Colpitts网格多涡卷超混沌系统[12]作为驱动系统，其状态方程为

(6)

式(6)中，FM(x2)和FN(x4)为三角波函数，其数学表达式为

(7)

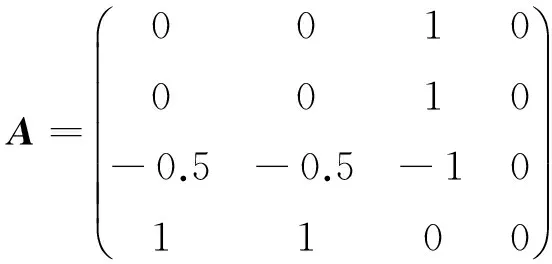
选取超混沌Lorenz系统[13]为响应系统：

(8)

由系统(8)得

取矩阵k = diag (2, 2, 2,2)得

显然，对称阵(A-k)T+(A-k)负定。

取K = 20，根据式(4)，可得同步控制器

(9)

图1　3×3涡卷超混沌吸引子Fig. 1　3×3-scroll chaotic attractors

图2　3×3涡卷时的同步误差曲线Fig. 2　Synchronous error curve in 3×3-scroll

当M=N= 1时，三角波函数-FM(x2) = -F1(x2)，FN(x4) =F1(x4)，系统(6)产生3×3涡卷超混沌吸引子如图1所示，系统(6)与系统(8)的同步误差曲线如图2所示；当M= 1，N= 2时，三角波函数-FM(x2)不变，FN(x4)由F1(x4)变为F2(x4)，系统(6)产生3×5涡卷超混沌吸引子如图3所示；系统(6)与系统(8)的同步误差曲线如图4所示。

图3　3×5涡卷超混沌吸引子Fig. 3　3×5-scroll chaotic attractors

图4　3×5涡卷时的同步误差曲线Fig. 4　Synchronous error curve in 3×5-scroll

当M= 2，N= 1时，三角波函数-FM(x2) 由-F1(x2)变为-F2(x2)，FN(x4)由F2(x4)变为F1(x4)，系统(6)产生5×3涡卷超混沌吸引子如图5所示；系统(6)与系统(8)的同步误差曲线如图6所示。

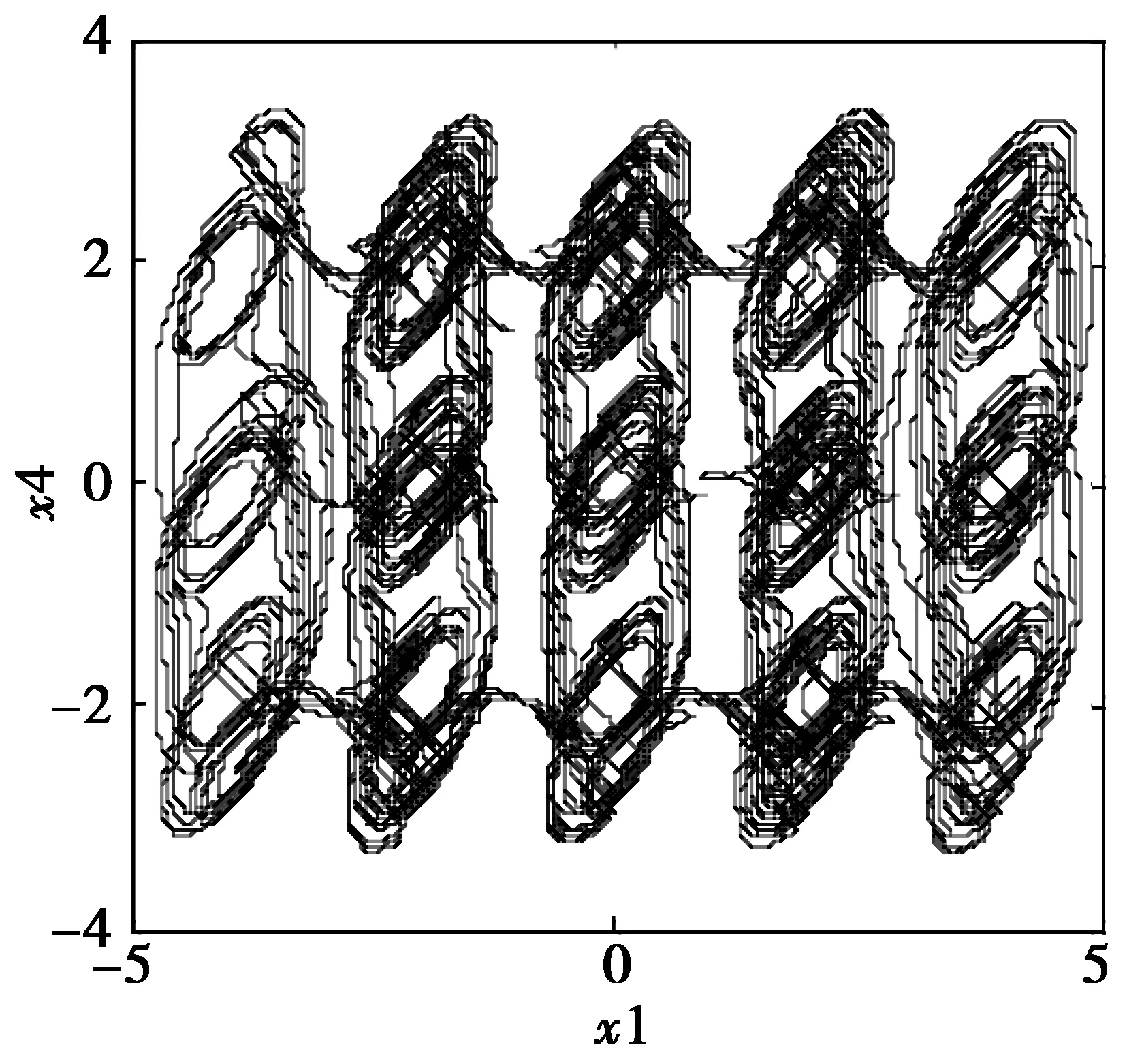
图5　5×3涡卷超混沌吸引子Fig. 5　5×3-scroll chaotic attractors

从图1—图6可以看出，三角波函数-FM(x2)在-F1(x2)和-F2(x2)交替变化和三角波函数FN(x4)在F1(x4)和F2(x4)交替变化时，系统(6)将交替产生3×3、3×5和5×3涡卷超混沌吸引子，而所设计的同步控制器式(9)不变，系统(6)和系统(8)却一直处于同步状态。数值仿真结果与理论推导结果一致，证明了同步方法所设计的控制器的有效性。

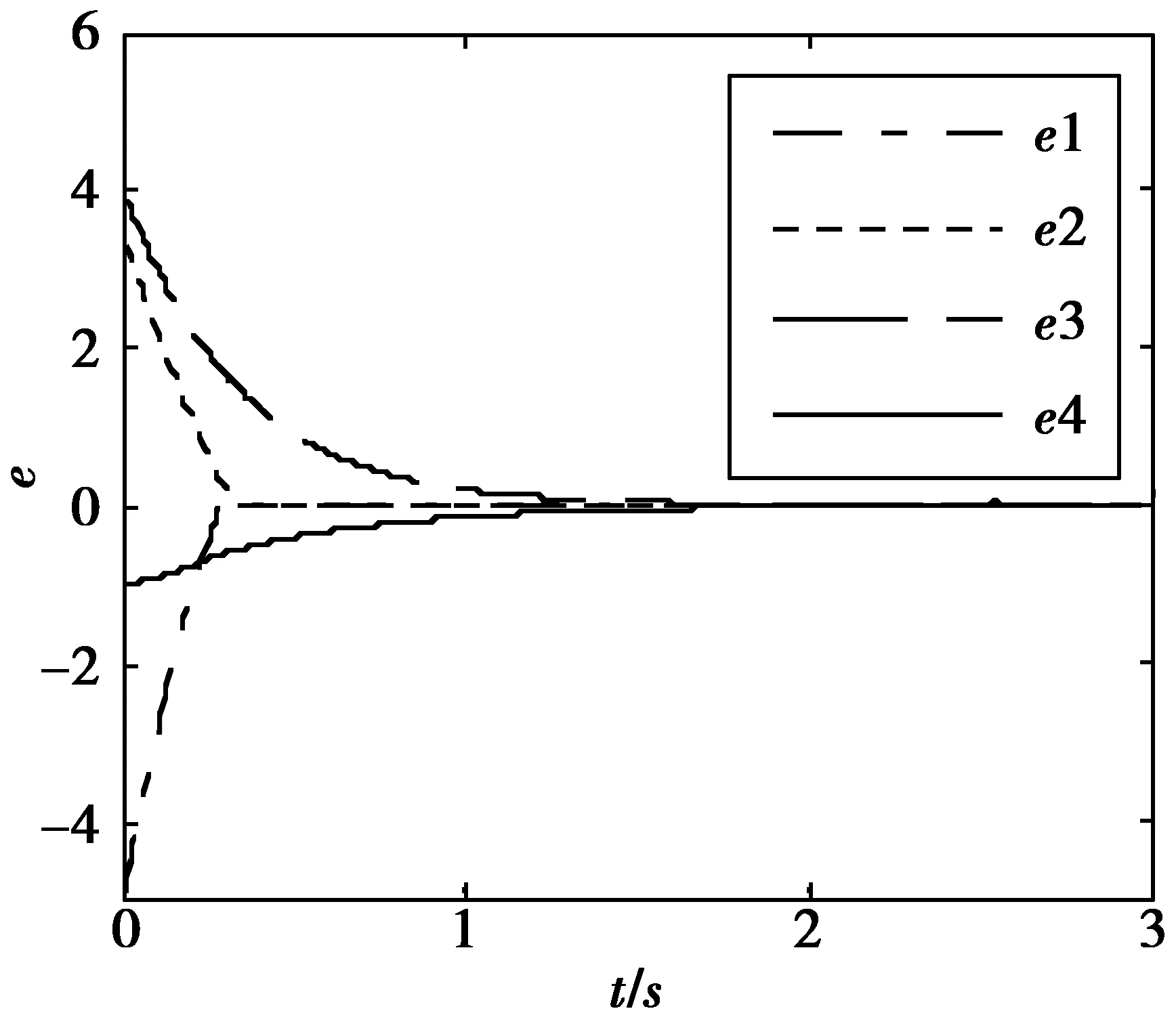
图6　5×3涡卷时的同步误差曲线Fig. 6　Synchronous error curve in 5×3-scroll

3　结　论

巧妙地应用符号函数，设计了一种不含多涡卷混沌系统的非线性函数的同步控制器。同步控制器能在保持不变的情况下，使吸引子个数连续变化的多涡卷混沌系统与其响应系统保持同步状态。由于多涡卷混沌系统在吸引子个数连续变化下产生的混沌信号较固定下产生的混沌信号更复杂，因此实现多涡卷混沌系统在吸引子个数连续变化下的同步，在保密通信中有较大的应用价值。

[1] 陈红.多涡卷混沌吸引子同步的双控制器[J].电机与控制学报,2008,12(2): 190-194

CHEN H.Double-controller of Synchronizing Chaotic Systems with Multi-scroll Attractors [J].Electric Machines and Control,2008,12(2):190-194

[2] CHEN L,SHI Y D,WANG D S.Adaptive Generalized Synchronization Between Chen System and a Multi-scroll Chaotic System [J].Chin Phys B,2010,19(10):100-105

[3] XU F Q,YU P.Chaos Control and Chaos Sychronization for Multi-scroll Chaotic Attractors Generated Using Hyperbolic Functions [J].J Math Anal Appl,2010,62(1):252-274

[4] 马美玲,闵富红,邵书以,等.基于符号函数的注入反馈式蔡氏电路同步控制[J].物理学报,2014,63(1):101-107

MA M L,MIN F H,SHAO S Y,et al.Chaotic Synchronization Control of Chua’s Circuit by Injected Feedback Based on the Symbolic Function [J].Acta Phys.Sin.,2014,63(1):101-107

[5] XU F,YU P,LIAO X X.Synchronization and Stabilization of Multi-scroll Integer and Fractional Order Chaotic Attractors Generated Using Trigonometric Functions [J].Int J Bifur Chaos,2013,23(8):135-145

[6] JL E,LEZ S J.Generalized Multistable Structure via Chaotic Synchronization and Preservation of Scrolls [J].Journal of the Franklin Institute,2013,350(10):2853-2866

[7] 吴忠强,邝玉.多涡卷混沌系统的广义同步控制[J].物理学报,2009,58(10):6823-6827

WU Z Q,KUANG Y.Generalized Synchronization Control of Multi-scroll Chaotic Systems [J].Acta Phys Sin,2009,58(10):6823-6827

[8] CUI D L,ZHANG X L,MA X X.Synchronization for a Class of Multi-scroll Chaotic Systems Via Sliding Mode Control [J].International Journal of Applied Mathematics and Statistics,2013,49(19):135-142

[9] ZHANG X L,MA X,CUI D L.Generalized Synchronization for Multidirectional Saturated Multi-scroll Chaotic Systems [J].International Journal of Applied Mathematics and Statistics,2013,49(19):248-255

[10] GUI Z F,WU X F,CHEN Y.Global Synchronization of Multi-scroll Saturated Chaotic Systems via Single-state Linear Feedback Control [J].Int J Mod Phys B,2013,27(5):135139

[11] 胡玉婷 李东 张兴鹏.参数未知的分数阶混沌系统的自适应追踪控制[J].重庆工商大学学报(自然科学版),2015,32(3):1-7 HU Y T,LI D,ZHANG X P.Adaptive Tracking Control of Fractional Order Chaotic Systems with Unknown Parameters.Journal of Chongqing Technology and Business(Natural Science Edition) [J].2015,32(3):1-7

[12] 包伯成,刘中,许建平,等.基于Colpitts振荡器模型生成的多涡卷超混沌吸引子[J].物理学报,2010,59(3):1540-1548

BAO B C,LIU Z,XU J P,et al.Generation of Multi-scroll Hyperchaotic Attractor based on Colpitts Oscillator Model[J].Acta Phys Sin,2010,59(3):1540-1548

[13] 王兴元,王明军.超混沌Lorenz系统[J].物理学报,2007,56(9):5136-5141

WANG X Y,WANG M J.Hyperchaotic Lorenz System[J].Acta Phys.Sin.,2007,56(9):5136-5141

责任编辑：田静

A Synchronous Method of Multi-scroll Chaotic System with Continuously Changing the Quantity of Attractors

HUANG Yun,ZHAO Wei-feng

(Asset Management Department, Chongqing University of Posts and Telecommunications, Chongqing 400065, China)

In this paper, a synchronous method of multi-scroll chaotic system with continuously changing the quantity of attractors is proposed. Based on Lyapunov stability theory, a synchronous controller is designed. The controller makes the multi-scroll chaotic system with continuously changing the quantity of attractors remain synchronization at all time, while the controller is invariable. Finally, taking synchronization between grid multi-scroll Colpitts hyper-chaotic system and hyper-chaotic Lorenz system as an example, a numerical simulation study is carried out. The simulation results show the effectiveness of the controller.

chaos; multi-scroll chaotic system; hyperchaotic Lorenz system; synchronization

10.16055/j.issn.1672-058X.2016.0005.004

2015-10-10；

2016-04-05.

重庆市自然科学基金(CSTCJJA40039);重庆市自然科学基金(CSTC2012JJA40008);重庆市教委科学技术研究项目(KJ1400406);重庆市教委科学技术研究项目(KJ1400410).

黄沄(1981-)，男，重庆南岸人，工程师，硕士，从事非线性电路分析与计算机应用研究.

O545

A

1672-058X(2016)05-0016-05