L0正则化增量正交投影非负矩阵分解的目标跟踪算法
2016-10-18王海军葛红娟
王海军, 葛红娟
(1. 南京航空航天大学民航学院, 江苏 南京 211106; 2. 滨州学院山东省高校航空信息技术重点实验室, 山东 滨州 256603)
L0正则化增量正交投影非负矩阵分解的目标跟踪算法
王海军1,2, 葛红娟1
(1. 南京航空航天大学民航学院, 江苏 南京 211106; 2. 滨州学院山东省高校航空信息技术重点实验室, 山东 滨州 256603)
针对传统跟踪算法不能在复杂场景下进行有效跟踪的问题,提出一种基于L0正则化增量正交投影非负矩阵分解(incremental orthogonal projective non-negative matrix factorization,IOPNMF)的目标跟踪算法。在粒子滤波框架下采用IOPNMF算法在线获得跟踪目标基于部分的表示以构建模板矩阵,然后将每帧中的候选样本建立基于模板矩阵的线性表示,对表示系数进行L0正则化约束,并提出快速数值解法,同时引入粒子筛选机制,加快跟踪速度。实验结果表明,新算法能够解决跟踪过程中出现的遮挡、光照变化、运动模糊等影响跟踪性能的因素,具有较高的平均覆盖率和较低的平均中心点误差。
目标跟踪; L0正则化; 粒子筛选
0 引 言
目标跟踪是计算机视觉领域一项重要的研究课题,在交通流量控制、人机接口、视频监控等领域得到了广泛的应用。近年来,国内外学者对目标跟踪进行了大量的研究工作,大致可以分为两类:基于判别模型的目标跟踪[1-4]和基于生成模型的目标跟踪[5-7]。基于判别模型的方法将目标跟踪看成是一个二分类问题,将被跟踪的目标物体从众多的背景中分离出来。基于生成模型的方法把目标跟踪看成是从候选样本中寻找与目标模板中最相似的区域。这类方法由于跟踪结果比较鲁棒,得到了国内外许多学者的关注。例如,文献[8]提出增量视觉跟踪(incremental visual tracking,IVT)算法,该方法将每个候选样本用主成分分析(principal component analysis, PCA)基向量图像的线性组合来表示,并采用增量主成分分析方法对PCA基向量进行更新以适应跟踪目标外观的变化,取得了不错的跟踪效果。文献[9]将稀疏表示应用到目标跟踪领域,提出L1最小化跟踪算法,用目标模板和正负琐碎模板组成字典矩阵对候选样本进行线性表示,并对目标模板进行在线更新,获得了较为精确的跟踪结果。文献[10]提出加速近似梯度算法(accelerated proximal gradient,APG)求解L1最小化问题,从而实现快速的目标跟踪。文献[11]提出基于稀疏原型的跟踪算法,将候选样本由正交基向量和琐碎模板稀疏线性表示,同时提出考虑遮挡机制的观测模型更新方式。文献[12]提出基于增量正交映射非负矩阵分解的目标跟踪算法,能够增量获得目标模板基于部分的表示,取得较好的跟踪效果。
上述提到的算法都要对表示系数进行稀疏求解,希望得到的表示系数中0的个数尽可能多,文献[13]提出用L0正则化对系数进行稀疏求解,但是L0正则化是不确定性多项式-难(non-deterministic polynomial-hard,NP-hard)问题,许多学者使用L1正则化代替L0正则化进行求解。但是L0正则化是对表示系数的硬约束,用L1正则化简单的代替L0正则化,会引起性能的下降。本文采用增量正交映射非负矩阵分解获得模板矩阵的部分表示,并采用L0正则化对表示系数进行约束,提出一种新的系数求解算法,同时对采样粒子进行筛选,减少了运算复杂度,提高了跟踪速度。
1 增量正交映射非负矩阵分解
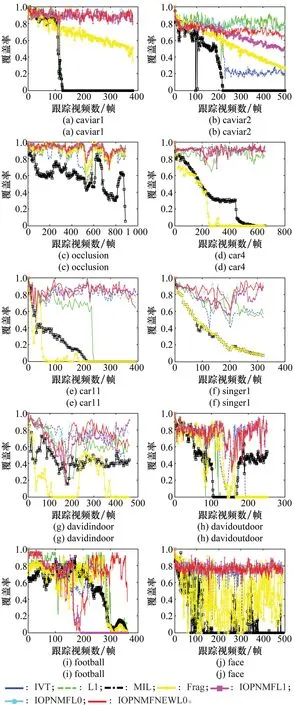
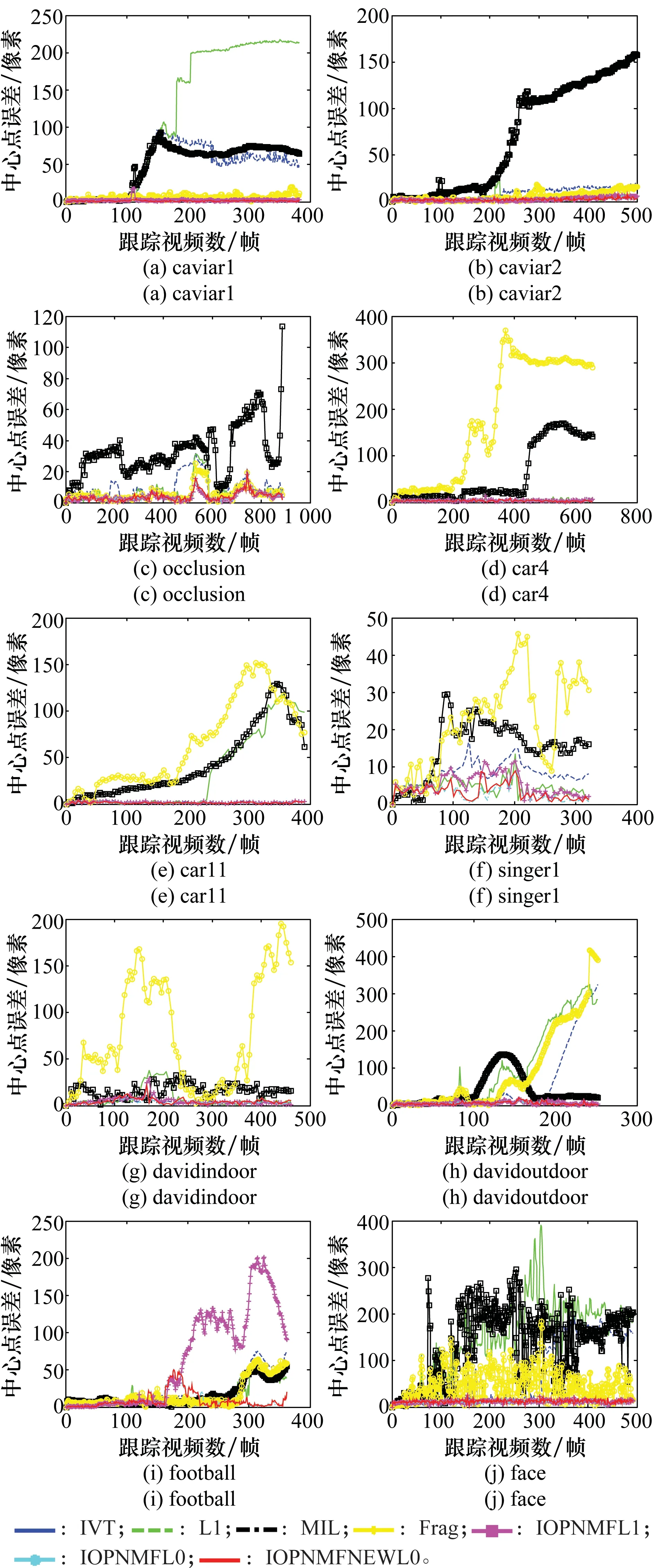
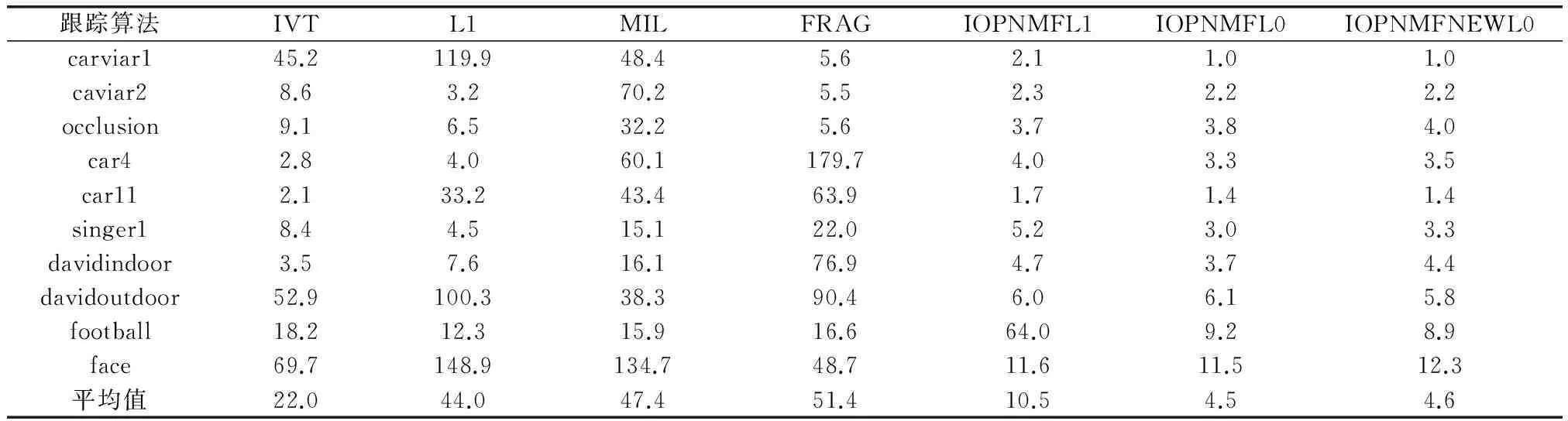
非负矩阵分解[14](non-negative matrix factorization, NMF)假设高维非负矩阵Y=[y1,y2,…,yn]∈Rd×n(其中,yi为d维列向量,n为列向量的个数)可以分解为两个非负矩阵W∈Rd×k和H∈Rk×n的乘积(k (1) (2) 目标函数Jr对Wr进行求导,即 (3) (4) (5) 2.1L1正则化的目标表示 文献[12]提出基于L1正则化增量正交映射非负矩阵分解的目标跟踪(object tracking via IOPNMF with L1 regularization,IOPNMFL1)算法,假设观测目标(候选样本)可以近似由IOPNMF基向量矩阵和琐碎模板组成的字典矩阵线性表示,即 (6) 式中,I代表观测目标(候选样本);W为IOPNMF基向量矩阵,且基向量矩阵之间相互正交,即WTW=E;z为对应的表示系数;E代表单位矩阵,即琐碎模板;e为大小任意且稀疏的误差项,可被看作是琐碎模板对应的表示系数。表示系数z和e可通过式(7)进行求解: (7) 式中,‖·‖2和‖·‖1分别表示L2范数和L1范数;λ为正则化参数。IOPNMFL1算法虽然对异常噪声进行显式处理,相比传统的L1正则化算法提高了运算速度,但是对表示系数z没有进行任何约束,仍然是不稀疏的,当跟踪视频中出现遮挡时,不加约束的表示系数z不能有效地去除遮挡。 2.2L0正则化的目标表示 为了解决IOPNMFL1算法存在的问题,对表示系数z进行约束,进行L0正则化,即式(7)修改为 (8) 式中,‖·‖0为L0范数;γ为正则化参数。 2.3L0正则化的数值解法 式(8)中,表示系数z和e的求解可以分解为两个子问题: (9) (10) 式(9)中,ek+1的求解可通过软阈值方法求解,即给定zk,ek+1=Sλ(I-Wzk),其中Sλ(x)=max(|x|-λ,0)sgn(x)为软阈值函数,sgn(·)为符号函数。 式(10)zk+1的求解,假定 (11) 式中,F是可微凸函数,则其梯度为 (12) 考虑式(10)在qk+1处的二阶近似,同时增加一个近似项,则式(10)可近似为 (13) 式中,L为惩罚参数。 由文献[15],可得式(13)的解为 (14) 求解式(8)求解的算法流程如下: 初始化z0=z-1=0,e0=e-1=0,t0=t-1=1 While不收敛或不终止do 步骤 1ek+1=Sλ(I-Wzk) 步骤 3 k←k+1 Endwhile (15) 式中,p(xt|xt-1)表示描述连续两帧状态转换的运动模型;p(It|xt)表示在状态变量xt条件下,观测样本属于跟踪目标概率大小的观测模型。 3.1运动模型 3.2观测模型 用观测模型来评估每个候选样本属于跟踪目标的可能性,即 (16) 式中,W为IOPNMF基向量矩阵;μ为IOPNMF子空间的均值;ξ为常参数;上标i表示第i个粒子;d(Ii;W,μ)为最小软阈值均方距离,即 (17) 3.3粒子筛选 传统算法是对所有粒子(通常选取粒子数目为600个)进行求解,但是这样会导致计算量增加。为加快运算速度,本文采用局部归一化距离准则[16]对候选粒子进行L0正则化计算观测模型之前进行筛选,滤掉可能不是目标的粒子,从而提高运算速度。局部归一化距离的定义为 (18) 仿真实验平台为Windows8操作系统,Inter(R)Core(TM)i7-5500UCPU@2.4GHz,8GB内存,采用Matlab2014进行软件仿真。实验参数为:λ=0.2,γ=0.024,L=6。IOPNMF子空间的维数为16,每一帧中采样粒子的数目为600,每个采样粒子对应的候选样本缩放为32×32像素,每5帧对观测模型进行更新。本文提出的算法简写为IOPNMFL0,带有筛选机制的算法简写为IOPNMFNEWL0。 为了验证本文所提算法的有效性,选用10个具有代表性的视频与5种算法进行对比,算法包括:IVT(incrementalvisualtracking)[8],MIL(multipleinstancelearning)[1],L1[9],Frag(fragments-basedtracking)[17],IOPNMFL1[12]。 4.1定性对比 严重遮挡:遮挡是影响跟踪性能的重要因素,图1(a)和图1(b)视频中目标人物分别进行由近到远以及由远到近地移动,不仅存在运动场景的光照变化,而且有旁边其他相似移动人物的遮挡,如图1(a)视频中第115帧,图1(b)视频中第200帧,目标人物几乎被完全遮挡。IOPNMFNEWL0、IOPNMFL0、IOPNMFL1由于采取IOPNMF分解获得目标人物基于部分的表示,同时用仿射变换建模跟踪过程中的尺度变化,成功实现整个过程中目标人物的跟踪。MIL算法由于采用haar特征对跟踪目标进行描述,容易受到周围相似目标的干扰,所以当出现遮挡时,跟踪结果都偏移到干扰人物上,导致跟踪失败。图1(c)视频中目标人物头部位置基本不变,但是存在来自目标人物左边、右边以及下方书本的严重遮挡,且书本的颜色和目标人物头发颜色很相似,跟踪过程非常容易受到干扰。从跟踪结果来看,大部分方法整个过程都实现了成功跟踪,但是IVT、L1、MIL、FRAG存在少量的偏移,跟踪准确性方面比IOPNMFNEWL0、IOPNMFL0、IOPNMFL1有所下降。 图1 不同算法在遮挡视频中的跟踪结果对比Fig.1 Comparision of tracking results on occluded videos by different algorithms 光照变化:光照变化严重影响算法的跟踪性能。图2(a)视频中汽车由近处向远处行进,道路以及周围环境与汽车本身的颜色非常接近,同时需要通过桥洞以及树木的阴影区域,存在光照变化;图2(b)视频中,汽车在夜晚道路上行进,对面汽车远光灯以及道路两旁树木上的灯光严重影响算法对目标汽车的跟踪;图2(c)视频中,舞台灯光照射白衣歌者,很难对白衣歌者与灯光进行区分跟踪,同时由于摄像机位置的变化,歌者的尺度也发生变化;图2(d)视频中,不仅存在光照变化,而且人物头部还存在姿态变化。从跟踪结果来看,Frag算法容易受光照变化影响,偏离跟踪目标,如图2(a)视频中第250帧,图2(b)视频中第170帧、240帧,图2(c)视频中第290帧。MIL算法由于没有考虑跟踪目标的尺度变换,所以跟踪框虽然也基本上能够实现对目标物体进行跟踪,但是跟踪精度下降。L1算法在对模板矩阵更新时,没有考虑遮挡因素,导致视频跟踪过程中出现精度下降。 背景杂乱:图3(a)、图3(b)视频中不仅存在背景杂乱,而且跟踪目标存在姿态变化以及周围相似物体的干扰。IOPNMFNEWL0、IOPNMFL0由于对表示系数进行L0约束,相比其他算法,跟踪性能一直比较稳定,能够实现准确跟踪。 运动模糊:图4中face视频不仅目标人物存在剧烈运动导致目标人物头部模糊,而且摄像机也存在快速突然晃动,严重影响算法的跟踪性能。实验结果可以看出,只有IOPNMFNEWL0、IOPNMFL0、IOPNMFL1能够一直稳定进行跟踪,其他算法都偏离目标,导致跟踪失败。 4.2定量对比 图2 不同算法在光照变化视频中的跟踪结果对比Fig.2 Comparision of tracking results on videos with illumination change by different algorithms 图3 不同算法在背景杂乱视频中的跟踪结果对比Fig.3 Comparision of tracking results on videos with background clutter by different algorithms 图4 不同算法在运动模糊视频中的跟踪结果对比(Face)Fig.4 Comparision of tracking results on videos with motion blur by different algorithms (Face) 图5 不同算法的覆盖率对比Fig.5 Comparison of overlap rate by different algorithms 图6 不同算法的中心点误差对比Fig.6 Comparision of center point error by different algorithms 跟踪算法IVTL1MILFRAGIOPNMFL1IOPNMFL0IOPNMFNEWL0caviar10.270.270.250.680.880.910.90caviar20.450.810.250.550.660.770.72occlusion0.840.870.590.890.920.920.92car40.920.840.340.220.890.900.90car110.800.430.170.080.840.830.84singer10.660.700.330.340.770.850.85davidindoor0.710.620.440.190.700.770.74davidoutdoor0.510.340.400.390.760.760.75 续表1 表2 不同算法的平均中心点误差对比 提出一种基于L0正则化IOPNMF的目标跟踪算法。首先采用增量正交投影算法,在线获得候选样本基于部分的表示,然后粒子滤波的框架下,以IOPNMF基向量构建跟踪算法的观测模型,对表示系数进行L0正则化约束,提出快速数值解法。同时引入粒子筛选机制,加快跟踪速度。实验结果表明,本文算法算法具有较高的覆盖率和较低的中心点误差,能够实现鲁棒的跟踪。 [1] Babenko B, Yang M H, Belongie S. Robust visual tracking with online multiple instance learning[J].IEEETrans.onPatternAnalysisandMachineIntelligence, 2011, 33(8): 1619-1632. [2] Zhang K H, Zhang L, Yang M H. Fast compressive tracking[J].IEEETrans.onPatternAnalysisandMachineIntelligence, 2014, 36(10): 2002-2015. [3] Zhang K H, Zhang L, Yang M H, et al. Robust object tracking via adaptive feature selection[J].IEEETrans.onCircuitsandSystemsforVideoTechnology, 2013, 23(11): 1957-1967. [4] Wu J H, Tang L B, Zhao B J, et al. Visual dictionary and online multi-instance learning based object tracking[J].SystemsEnginee-ringandElectronics, 2015, 37(2): 425-435. (吴京辉, 唐林波, 赵保军, 等. 基于视觉字典的在线多示例目标跟踪[J]. 系统工程与电子技术, 2015, 37(2): 425-435.) [5] Wang H J, Zhang S Y. Algorithm of object-tracking based on collaborative representation[J].JournalofUniversityofChineseAcademyofSciences, 2016, 33(1): 135-143. (王海军, 张圣燕. 基于协同表示的目标跟踪算法[J]. 中国科学院大学学报, 2016, 33(1): 135-143.) [6] Ma B, Hu H W, Shen J B, et al. Linearization to nonlinear learning for visual tracking[C]∥Proc.oftheIEEEInternationalConferenceonComputerVision, 2015: 4400-4407. [7] Ma B, Shen J, Liu Y, et al. Visual tracking using strong classifier and structrual local sparse descriptors[J].IEEETrans.onMultimedia, 2015, 17(10): 1818-1828. [8] Ross D, Lim J, Lin R S, et al. Incremental learning for robust visual tracking[J].InternationalJournalofComputerVision, 2008, 77(1): 125-141. [9] Xue M, Ling H B. Robust visual tracking using L1 minimization[C]∥Proc.oftheIEEEInternationalConferenceonComputerVision, 2009: 1436-1443. [10] Bao C L, Wu Y, Ling H B, et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]∥Proc.oftheIEEEConferenceonComputerVisionandPatternRecognition, 2012: 1830-1837. [11] Wang D, Lu H C, Yang M H. Online object tracking with sparse prototypes[J].IEEETrans.onImageProcessing, 2013, 22(1): 314-325. [12] Wang D, Lu H C. On-line learning parts-based representation via incremental orthogonal projective non-negative matrix factorization[J].SignalProcessing, 2013, 93(6): 1608-1623. [13] Dohoho D L. Compressed sensing[J].IEEETrans.onInformationTheory, 2006, 52(4): 1289-1306. [14] Lee D, Seung H. Learning the parts of objects by non-negative matrix factorization[J].Nature, 1999(401): 788-791. [15] Liu R S, Bai S S, Su Z X, et al. Robust visual tracking via L0 regularized local low-rank feature learning[J].JournalofElectronicImaging, 2015, 24(3): 033012. [16] Wang D, Lu H C, Bo C J. Visual tracking via weighted local cosine similarity[J].IEEETrans.onSystems,Man,andCyberneticsPartB, 2015, 45(9): 1838-1850. [17] Adam A, Rivlin E. Robust fragments-based tracking using the integral histogram[C]∥Proc.oftheIEEEConferenceonComputerVisionandPatternRecognition, 2006: 798-805. Object tracking via incremental orthogonal projective non-negative matrix factorization with L0 regularization WANG Hai-jun1,2, GE Hong-juan1 (1. College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106,China;2.KeyLaboratoryofAviationInformationTechnologyinUniversityofShandong,BinzhouUniversity,Binzhou256603,China) In order to solve the problem of tracking failure in complex scenes by traditional object tracking algorithms, a new object tracking algorithm based on incremental orthogonal projective non-negative matrix factorization (IOPNMF) with L0 regularization is presented. In the framework of the particle filter, template matrix is obtained on the part-based representation of the tracked object by the IOPNMF algorithm. The candidates in each frame are linearly representated by the template matrix. The representation coefficients are constrained by the L0 regularization while a fast numerical solution is proposed. At the same time, the particle selection mechanism is introduced to speed up the tracking speed. Experimental results show that the proposed algorithm can effectively overcome the influence of occlusion, illumination change, and motion blur, with higher average overlap rate and lower average center point error. object tracking; L0 regularization; particle selection 2016-03-17; 2016-07-01;网络优先出版日期:2016-08-05。 山东省自然科学基金高校、科研单位联合专项计划(ZR2015FL009);滨州市科技发展计划(2013ZC0103);滨州学院科研基金(BZXYG1524)资助课题 TP 391 A 10.3969/j.issn.1001-506X.2016.10.29 王海军(1980-),男,讲师,博士研究生,主要研究方向为目标跟踪。 E-mail:whjlym@163.com 葛红娟(1966-),女,教授,博士,主要研究方向为电机与电器、交通信息工程及控制。 E-mail:allenge@nuaa.edu.cn 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160805.1524.004.html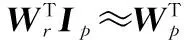

2 L0正则化增量正交映射非负矩阵分解的目标表示
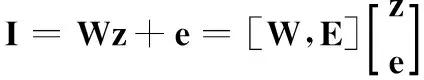
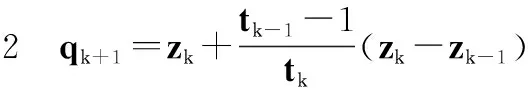
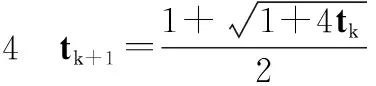
3 L0正则化增量正交映射非负矩阵分解的目标跟踪算法
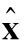

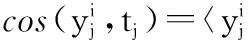
4 实验结果

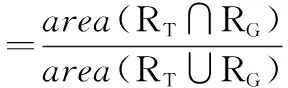





5 结 论
