模糊度固定解PPP/INS紧组合模型

刘　帅, 孙付平, 张伦东

(信息工程大学导航与空天目标工程学院, 河南 郑州 450001)



模糊度固定解PPP/INS紧组合模型

刘帅, 孙付平, 张伦东

(信息工程大学导航与空天目标工程学院, 河南 郑州 450001)

差分全球定位系统(difference global positioning system, DGPS)与惯性导航系统(inertial navigation system,INS)所构成的组合定位测姿系统已广泛应用于高精度移动测量领域,但由于需要基准站支持,该系统作业范围有限、作业复杂且成本高。模糊度为浮点解的精密单点定位(precise point positioning,PPP)与INS所构成的组合系统，虽不需要架设基准站,但定位精度有限且收敛时间较长,其原因就在于模糊度为浮点解。针对以上问题,提出将模糊度为固定解的PPP与INS进行紧组合,给出了该新组合详细的观测模型和系统模型。实测车载组合导航实验对新组合进行了验证,结果表明,仅用单台GPS接收机,只需约10余分钟就能获取首次固定解;一旦实现固定,新组合的位置误差迅速由分米级降低到稳定的厘米级。

精密单点定位; 模糊度固定; 惯性导航系统; 紧组合; 定位测姿

0　引　言

目前,载波相位差分全球定位系统(difference global positioning system, DGPS)与惯性导航系统(inertial navigation system,INS)所构成的组合定位测姿系统已经应用于车载移动测图、航空摄影测量、航空重力测量等高精度移动测量领域[1-3]。该系统使用基准站与流动站间的相位双差观测值跟INS进行组合,当模糊度成功固定时,该系统能够达到厘米级定位精度[4-5]。但是DGPS/INS组合系统存在着两个缺点:①在作业时,需要架设基准站于坐标控制点上,但对于海洋、丛林等区域的测量而言,极不便于架设基准站;②流动站要与基准站保持十几米甚至几千米以内的距离,以保证GPS观测误差的时空相关性,从而实现模糊度的成功固定,但当测区面积较大时,就需要同时架设多个基准站来确保定位精度,这增加了作业成本和复杂度。

精密单点定位(precise point positioning,PPP)技术只使用单台GPS接收机的双频相位、伪距观测值,在国际GNSS服务组织(international GNSS service, IGS)提供的精密星历和钟差等产品的支持下并考虑各项误差的精确改正,能够实现全球范围的静态毫米到厘米级、动态厘米到分米级的绝对定位[6-7]。若将PPP与INS组合,就有望克服DGPS/INS组合中存在的缺点,既不受作业距离限制,又能降低系统成本和复杂度,作业将更加灵活。不少学者在这方面开展了研究工作[8-13],但他们的研究全部集中在模糊度为浮点解的(即传统的)PPP与INS的组合上。由于模糊度为浮点解,导致了该组合有如下两个不足:①定位精度与观测条件(比如观测环境、时长、卫星数目等因素)密切相关,仅能获取厘米到分米范围的定位精度,与DGPS/INS组合的厘米级定位精度仍有差距；②通常需要几十分钟甚至数小时的初始收敛时间。

近些年,得益于不少学者的突破性工作,模糊度为固定解的PPP成为了可能[14-17]。阻碍PPP中模糊度难以固定的原因在于观测值中存在的偏差项。若能有效处理这些偏差项,就可以恢复模糊度的整数可固定特性。一旦模糊度成功固定,PPP定位精度可迅速由分米级提高到稳定厘米级。如果将模糊度固定解PPP与INS进行组合,既能有效地克服DGPS/INS组合的缺点,又能弥补模糊度浮点解PPP/INS组合的不足,有望实现无需架设基准站、无作业距离限制的高精度定位和测姿,可大大降低移动测量领域的作业成本和复杂度。因此,本文将针对这种新组合展开研究。由于紧组合较松组合有诸多优势,本文将研究集中在紧组合上。

首先给出模糊度固定解PPP观测模型、地心地固坐标系下的INS系统模型;随后构建模糊度固定解PPP/INS紧组合扩展卡尔曼滤波器(extended Kalman filter,EKF);最后通过实测车载组合导航实验,对新组合进行验证分析。

1　模糊度固定解PPP观测模型

单台GPS接收机的消电离层伪距、相位观测方程可写作:

(1)

(2)

(3)

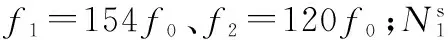
在接下来的推导之前,先定义4类钟差:

(4)

(5)

(6)

(7)

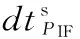
将式(4)和式(5)代入式(1)和式(2),经整理可得传统的模糊度为浮点解的PPP观测方程:

(8)

(9)

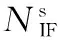
(10)

(11)

为避免同时估计两类接收机钟差,也是为了避免接收机钟差的建模难题,可对观测值星间求差,消掉接收机钟差。那么,对式(10)和式(11)星间单差可得:

(12)

(13)

式中,上标m和s分别指代基准星和非基准星;上标ms表示该量为星间单差量,由s量减去m量求得。在进行紧组合时,还应使用多普勒观测值。此处,直接给出星间单差的消电离层多普勒观测方程:

(14)

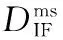
观察式(12)～式(14):对于卫星钟差与钟速,可使用精密卫星钟差产品改正;对于对流层延迟,它的干延迟使用模型改正,天顶方向湿延迟可进行估计;对于对流层延迟变化率,由于对流层变化缓慢,该项可忽略。此后,对这3式进行泰勒展开至一阶项,展开点取INS推算的位置、速度点,可得线性化后的观测方程:

(15)

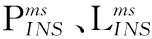
2　地心地固坐标系下INS系统模型

地心地固坐标系(e系)更适合于紧组合实现[18-19]。该坐标系下的惯性导航微分方程:

(16)

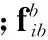
(17)

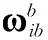
基于式(16),可推得INS系统模型:

(18)

式中,φe表示姿态失准角向量;I表示单位阵;符号[×]表示求斜对称矩阵;对于算例中战术级INS,假定它的加速度计和陀螺输出误差仅包含常值零偏加随机噪声,ba和bg分别表示b系下加速度计和陀螺的常值零偏向量,被建模成常数;εa和εg分别表示b系下加速度计和陀螺的随机噪声向量。

3　紧组合扩展卡尔曼滤波器设计

在模糊度固定解PPP/INS组合中,可采用松、紧两种组合结构,它们的区别是:松组合中使用PPP解算出的位置、速度结果与INS进行组合;紧组合中使用消电离层伪距、相位、多普勒观测值与INS进行组合。尽管紧组合实现复杂,但是当可见卫星数目少于4颗时,依旧可以进行量测更新[20],而且在观测噪声方差阵的确定、抵抗GPS观测粗差等方面也有优势。具体而言,一方面，输入到松组合滤波器中的PPP位置、速度是时间相关的,而且由于PPP需要经历收敛,很难确定收敛过程中的位置、速度方差大小;但是输入到紧组合滤波器中的观测值可认为在时间上是不相关的,而且可根据经验模型给出较准确的观测噪声方差。另一方面，紧组合可以直接在卫星的层次上发现并抵抗观测值粗差,对含粗差观测值直接进行降权处理。

因此本文直接研究紧组合结构,图1给出了具体的结构图。

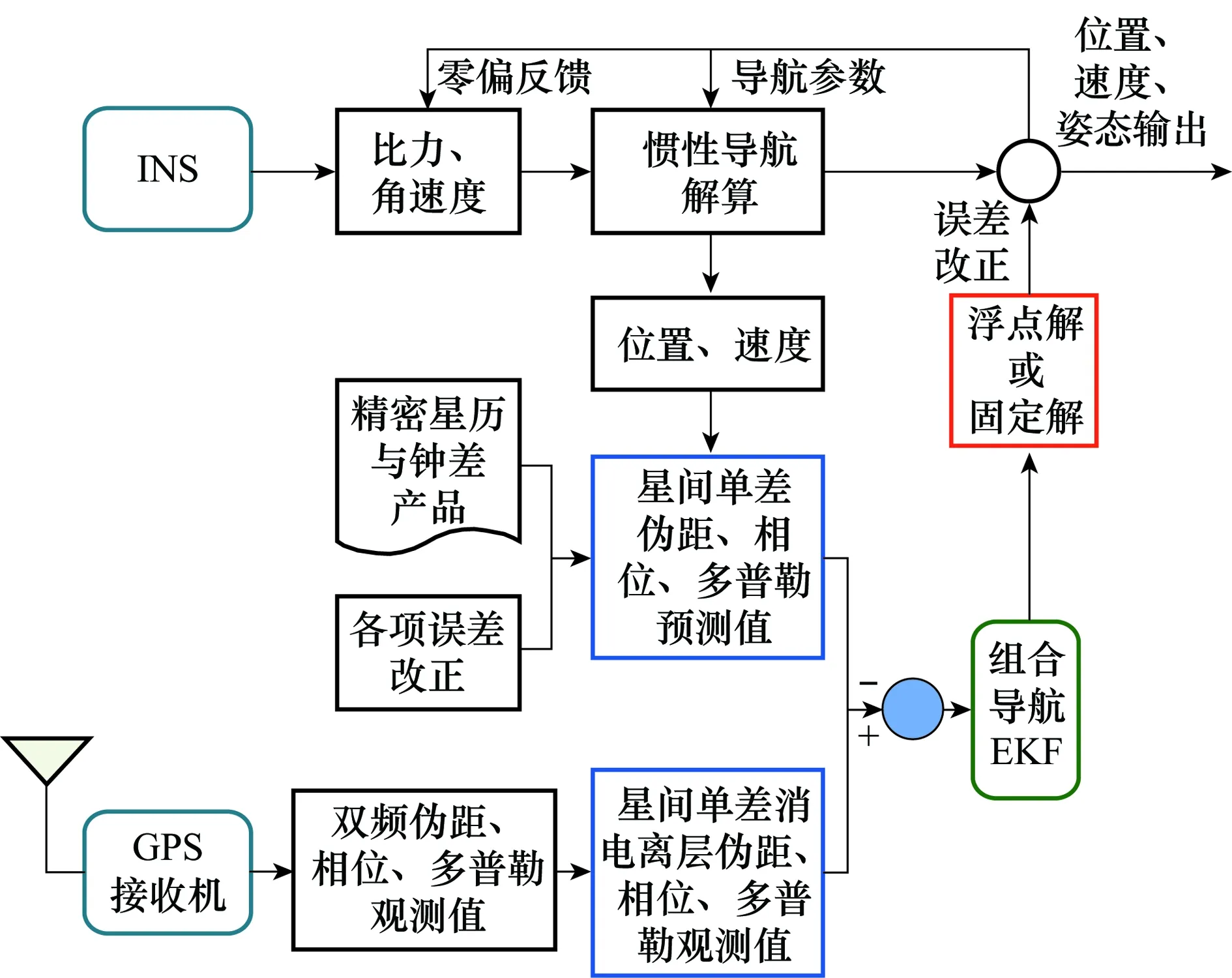
图1　PPP/INS紧组合结构图Fig.1　Architecture of tight integration of PPP and INS

基于式(15)和式(18),进行状态参数扩充,就可实现模糊度固定解PPP/INS紧组合扩展卡尔曼滤波器设计。

假设观测到了n颗卫星,并取高度角最高的卫星为基准星,将它的索引设为1,然后基于式(15)进行状态参数扩充,可得紧组合滤波器的观测模型:

(19)

基于式(18)进行状态参数扩充,可得紧组合滤波器的系统模型:

(20)

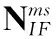
随机模型设置亦是紧组合滤波器能够取得理想结果的关键。对于观测噪声协方差阵(即R阵),笔者遵循的是经验模型(根据卫星高度角加权,伪距和相位的权比为100∶1);对于系统噪声功率谱密度阵(即Q阵),可以直接根据INS设备参数(速度随机游走和角度随机游走系数),再加上天顶方向对流层湿延迟随机游走噪声即可设置。

至此,就完成了模糊度固定解PPP/INS紧组合滤波器设计,之后便可滤波解算。实际上,该滤波器也可直接用于模糊度浮点解PPP/INS紧组合。它们的区别在于:模糊度浮点解PPP/INS紧组合仅用IGS发布的精密卫星钟差产品,所求星间单差消电离层模糊度始终保持浮点解;模糊度固定解PPP/INS紧组合还要使用CNES发布的精密卫星钟差产品和宽巷偏差产品,所求星间单差消电离层模糊度可按文献[17]所述逐级模糊度固定策略进行固定,一旦模糊度成功固定,该组合即可获取厘米级的定位结果。

4　算例分析

4.1数据背景介绍

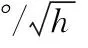
图2　跑车平面轨迹Fig.2　Plan trajectory of the car test

使用NovAtel公司出品的商用组合导航数据后处理软件InertialExplorer8.50(简称IE)对所采集数据以DGPS/INS紧组合模式进行后处理解算。该组合模式的后处理性能如表1所示。

表1　无GPS信号中断条件下IE软件后处理精度(DGPS/INS紧组合后处理平滑模式)

因为在后处理模式下使用了平滑算法,精度较好。论文以IE软件的解算结果作为参考值。

4.2解算结果分析

该组跑车实验中初始约9 min为静止段,使用此段数据进行初始对准,对其后的数据按照如下两种模式进行解算:①模糊度浮点解PPP/INS紧组合(传统组合);②模糊度固定解PPP/INS紧组合(新组合)。为了最原本的展示模式②实际的模糊度固定效果,未对模糊度进行固定保持等约束操作。若未成功固定,即直接输出浮点解。不过,本次实验观测条件较为理想,首次固定后的历元均可成功固定。

将解算结果与参考值做比较,得到位置、速度和姿态的误差值。解算中用到的GPS卫星颗数如图3所示。

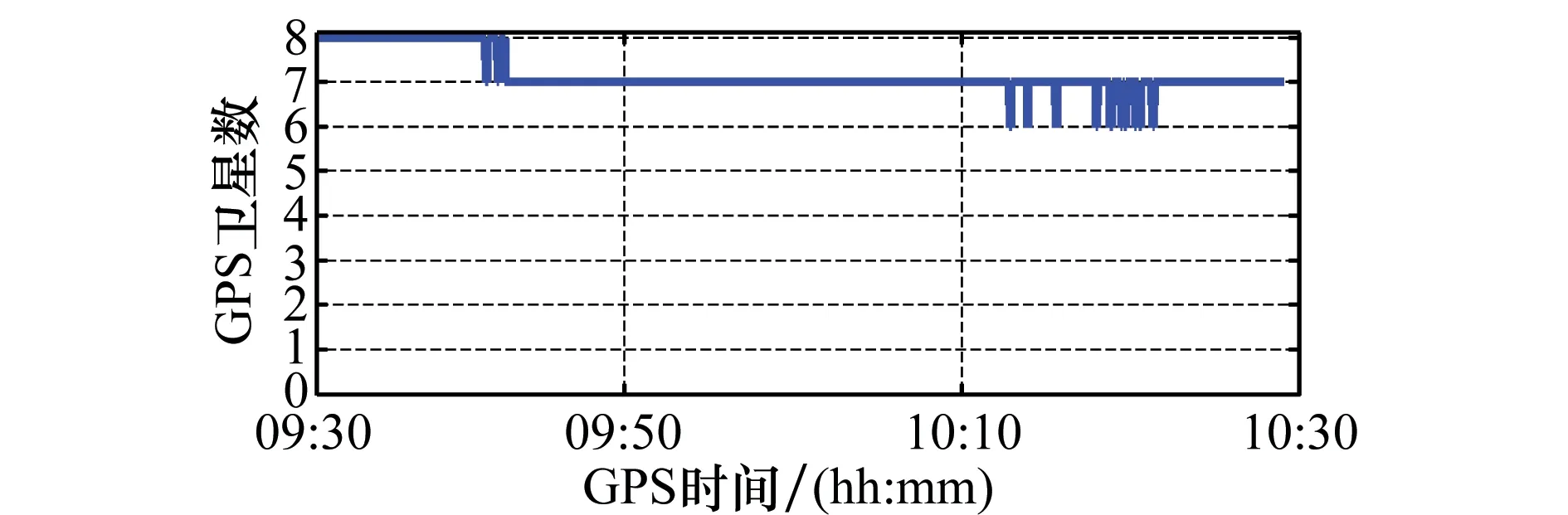
图3　观测到的GPS卫星数Fig.3　GPS satellite numbers

图4和图5分别给出了两种模式下的位置误差图。观察图5,约10 min,新组合就能实现首次固定,一旦模糊度固定成功,位置误差迅速由分米级降低至厘米级且较为稳定,具体可见该图中椭圆框部分。表2为对数据段最后30 min的位置误差进行统计,由统计结果也可看出新组合较传统组合的定位效果有显著改善。

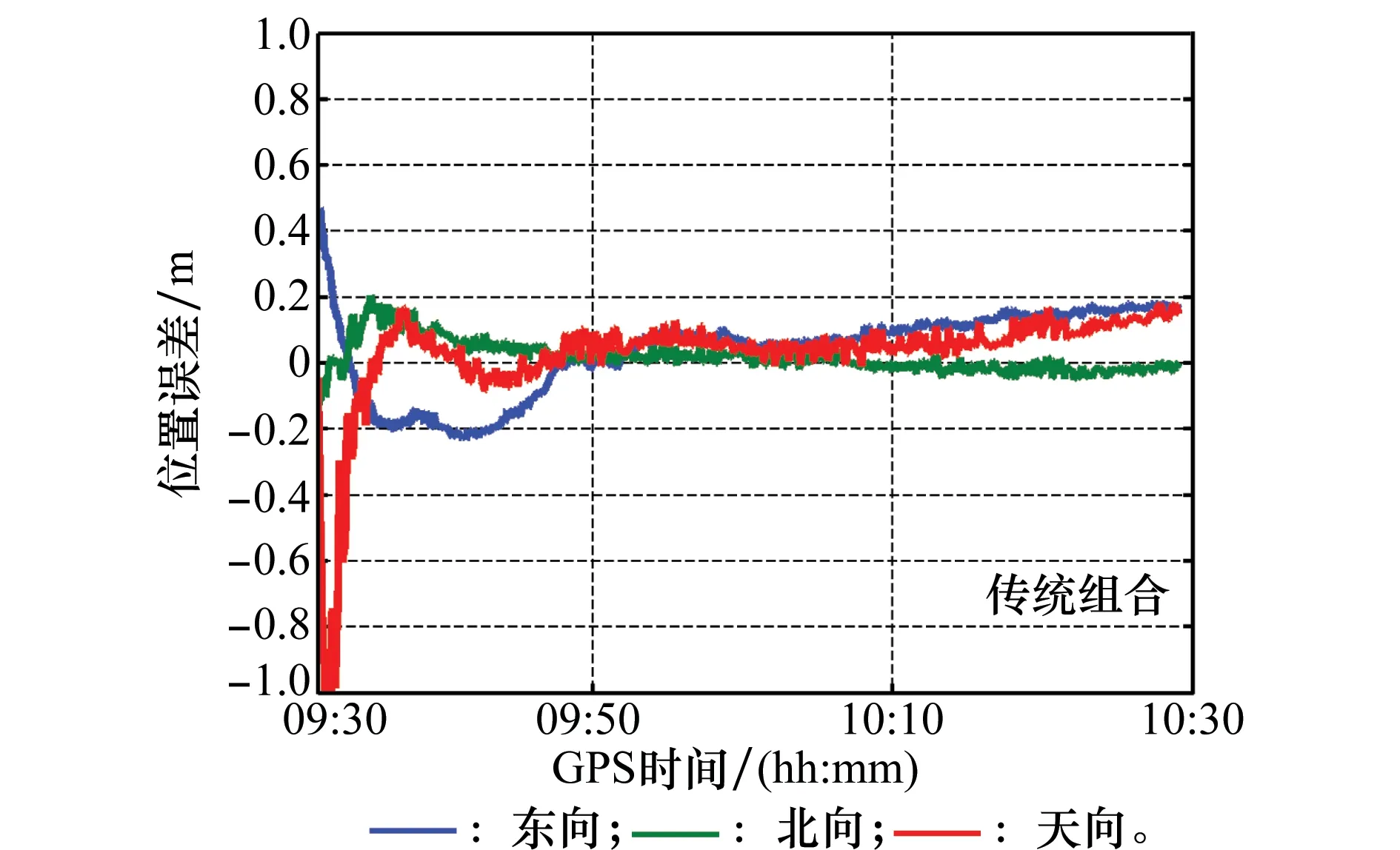
图4　模糊度浮点解PPP/INS紧组合位置误差Fig.4　Position error of the tight integration of ambiguity-float PPP and INS

图6和图7分别给出了新组合的速度误差和姿态误差,由于新组合相对于传统组合的主要优势在于模糊度固定后的位置精度的提升,而对速度、姿态的改进并不明显,因此传统组合的速度、姿态误差不再给出。但需注意,这里的“误差”实际上是新组合的解算结果与IE软件解算结果的差值,并非真正的误差。但是,从误差量级上仍能反映出:尽管解算模式不同,新组合与DNGSS/INS组合(IE软件)的速度、姿态解算结果是精度相当的。其中航向角的精度要略差,这是由于车载实验中,它的可观测度要差些。

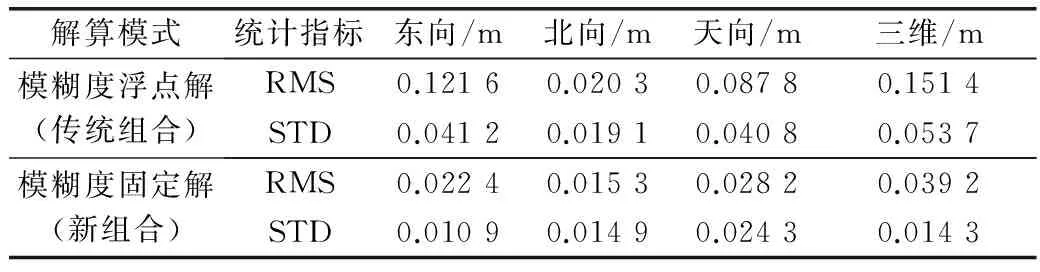
解算模式统计指标东向/m北向/m天向/m三维/m模糊度浮点解(传统组合)RMS0.12160.02030.08780.1514STD0.04120.01910.04080.0537模糊度固定解(新组合)RMS0.02240.01530.02820.0392STD0.01090.01490.02430.0143

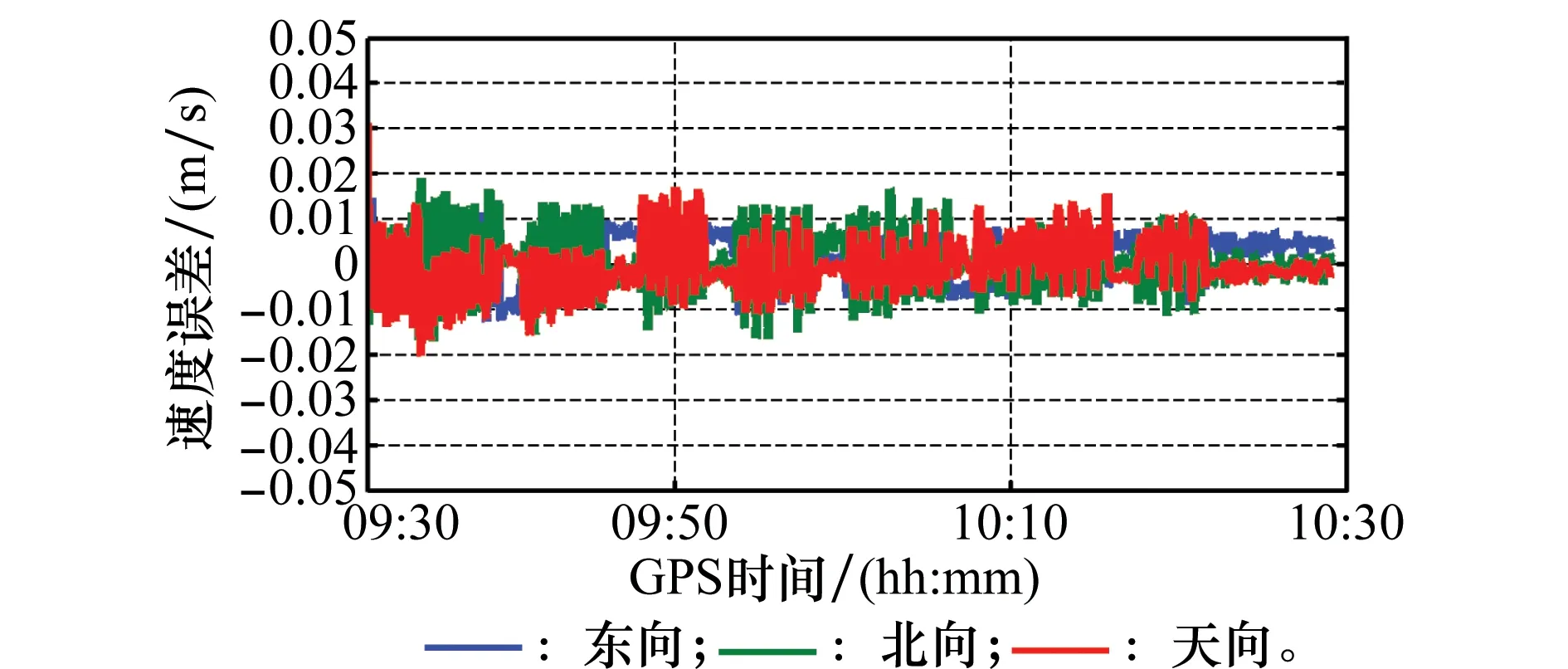
图6　模糊度固定解PPP/INS紧组合速度误差Fig.6　Velocity error of the tight integration of ambiguity-fixed PPP and INS

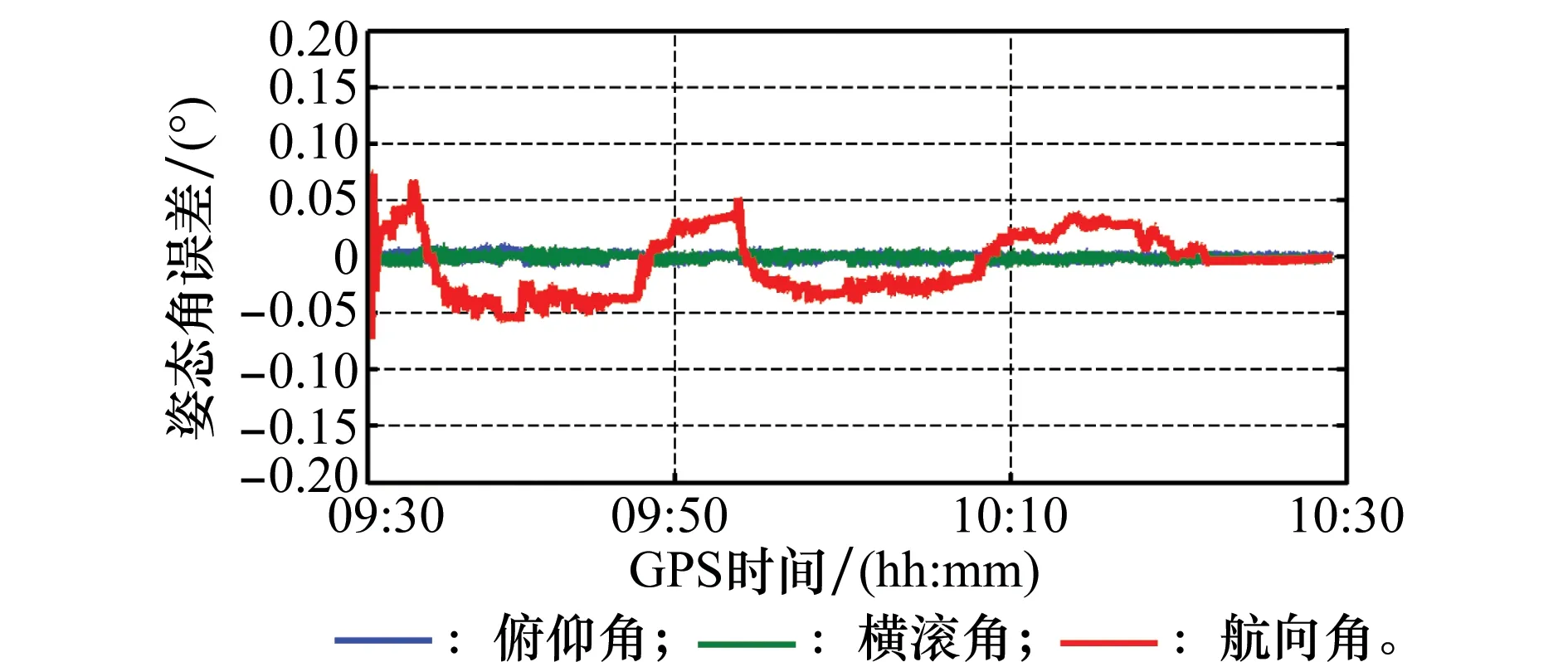
图7　模糊度固定解PPP/INS紧组合姿态误差Fig.7　Attitude error of the tight integration of ambiguity-fixed PPP and INS

图8和图9分别给出了新组合估计得到的加速度计和陀螺的常值零偏。对比两图可知,加速度常值零偏更容易估计和收敛。滤波收敛后的加速度计和陀螺常值零偏在量级上与所用INS的标称指标较为相符,也从侧面对新组合模型的正确性进行了验证。

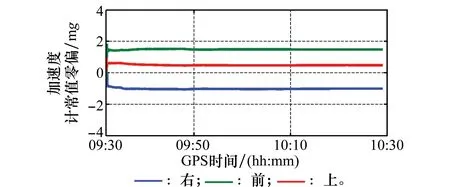
图8　加速度计常值零偏Fig.8　Accelerometer constant bias

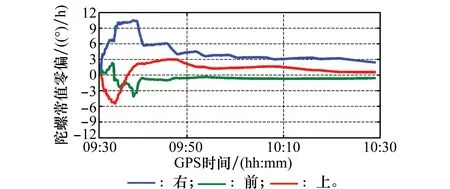
图9　陀螺常值零偏Fig.9　Gyroscope constant bias

5　结　论

本文对模糊度固定解PPP/INS紧组合模型进行了研究,给出了详细的观测模型和系统模型。实测车载组合导航实验表明:模糊度固定解PPP/INS紧组合仅用单台GPS接收机就能获取厘米级的定位性能,测速测姿精度也与IE软件中DGNSS/INS组合相当。

由于无需架设基准站,因此该组合特别适合大面积移动测绘,为测绘用户提供了新选择。但是,要把模糊度固定解PPP/INS紧组合系统推向实用,还需要增强系统的容错与质量控制能力。此外,由于在紧组合滤波器中加入了模糊度参数,导致计算负担显著增加,如何提高数值解算效率也值得研究。

[1] Skaloud J. Optimizing georeferencing of airborne survey systems by INS/DGPS[D]. Calgary: University of Calgary, 1999.

[2] Godha S, Cannon M E. GPS/MEMS INS integrated system for navigation in urban areas[J].GPSSolutions, 2007, 11(3):193-203.

[3] Cai S K, Wu M P, Zhang K D, et al. The first airborne scalar gravimetry system based on SINS/DGPS in China[J].ScienceChina:EarthSciences, 2013, 56(12): 2198-2208.

[4] Grejner-Brzezinska D A, Da R, Toth C. GPS error modeling and OTF ambiguity resolution for high-accuracy GPS/INS integrated system[J].JournalofGeodesy, 1998, 72(11): 626-638.

[5] Petovello M G, Cannon M, Lachapelle G. Benefits of using a tactical-grade IMU for high-accuracy positioning[J].JournaloftheInstituteofNavigation, 2004, 51(1): 1-12.

[6] Zumberge J F, Heflin M B, Jefferson D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J].JournalofGeophysicalResearch,1997,102(B3):5005-5017.

[7] Kouba J. A guide to using international GNSS service (IGS) products[EB/OL]. [2014-06-03]. http:∥igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGS ProductsVer21.pdf.

[8] Zhang Y, Gao Y. Integration of INS and un-differenced GPS measurements for precise position and attitude determination[J].JournalofNavigation, 2008, 61(1): 87-97.

[9] Roesler G, Martell H. Tightly coupled processing of precise point position (PPP) and INS data[C]∥Proc.oftheIONGNSS, 2009: 1898-1905.

[10] Shin E, Scherzinger B. Inertially aided precise point positioning[C]∥Proc.oftheIONGNSS, 2009: 1892-1897.

[11] Du S, Gao Y. Inertial aided cycle slip detection and identification for integrated PPP GPS and INS[J].Sensors, 2012, 12(11): 14344-14362.

[12] Abd Rabbou M, El-Rabbany A. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems[J].GPSSolutions, 2015, 19(4): 601-609.

[13] Liu S, Sun F P, Li H F, et al. Forward-backward-smoothing algorithm with application to tightly coupled PPP/INS data post-processing[J].JournalofChineseInertialTechnology, 2015, 23(1): 85-91. (刘帅, 孙付平, 李海峰, 等. 前后向平滑算法在精密单点定位/INS紧组合数据后处理中的应用[J]. 中国惯性技术学报, 2015, 23(1): 85-91.)

[14] Laurichesse D, Mercier F, Berthias J P, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J].JournaloftheInstituteofNavigation,2009,56(2):135-149.

[15] Collins P, Bisnath S, Lahaye F, et al. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing[J].JournaloftheInstituteofNavigation, 2010, 57(2): 123-135.

[16] Shi J, Gao Y. A comparison of three PPP integer ambiguity resolution methods[J].GPSSolutions, 2014, 18(4): 519-528.

[17] Liu S, Sun F P, Hao W L, et al. Modeling and effects analysis of PPP ambiguity fixing based on integer phase clock method[J].ActaGeodaeticaetCartographicaSinica, 2014, 43(12): 1230-1237. (刘帅,孙付平,郝万亮,等.整数相位钟法精密单点定位模糊度固定模型及效果分析[J].测绘学报,2014,43(12):1230-1237.)

[18] Wei M, Schwarz K. A strapdown inertial algorithm using an earth-fixed cartesian frame[J].Navigation:JournalofInstituteofNavigation, 1990, 37(2): 153-167.

[19] Zhao S H, Lu M Q, Feng Z M. Application of EKF and UKF in tightly-coupled integrated navigation system[J].SystemsEngineeringandElectronics,2009,31(10):2450-2454.(赵思浩,陆明泉,冯振明.EKF与UKF在紧耦合组合导航系统中的应用[J].系统工程与电子技术,2009,31(10): 2450-2454.)

[20] Luo D C, Wang S C, Zeng H G, et al. Simulation research on the technology of the tightly-coupled GPS/INS integration[J].SystemsEngineeringandElectronics, 2009, 31(12): 2929-2933. (罗大成, 王仕成, 曾洪贵, 等. 紧耦合GPS/INS组合导航技术仿真研究[J]. 系统工程与电子技术, 2009, 31(12): 2929-2933.)

Research on the tight integration of ambiguity-fixed PPP and INS

LIU Shuai, SUN Fu-ping, ZHANG Lun-dong

(School of Navigation and Aerospace Engineering, Information Engineering University, Zhengzhou 450001, China)

The positioning and attitude system based on the difference global positioning system/inertial navigation system (DGPS/INS) integration is widely used in the precise mobile surveying area. However, the DGNSS/INS integration requires the support of base stations, which limits the working range and increases the system cost and complexity. Although the ambiguity-float precise point positioning (PPP)/INS integration does not need base stations, it requires a lot of convergence time and its positioning accuracy is restricted, which are caused by the float ambiguities. A new integration that tightly fuses the ambiguity-fixed PPP and INS is proposed. The system and measurement models of the new integration are described in detail. Validation of the new integration by using the real vehicle test data is made. The test results show that only using a single receiver, the new integration can achieve its first fixed solution in about ten minutes; and once the ambiguities are successfully fixed, the positioning error dramatically declines from the decimeter level to the stable centimeter level.

precise point positioning (PPP); ambiguity-fixed; inertial navigation system (INS); tight integration; positioning and attitude determination

2015-04-08；

2016-04-01；网络优先出版日期：2016-06-02。

国家自然科学基金(41374027)资助课题

U 666.1

A

10.3969/j.issn.1001-506X.2016.10.24

刘帅(1986-),男,博士研究生,主要研究方向为精密单点定位及其与惯性导航系统的组合。

E-mail:liushuai-0115@163.com

孙付平(1964-),男,教授,博士,主要研究方向为惯性导航与组合导航算法。

E-mail:sun.fp@163.com

张伦东(1980-),男,讲师,博士,主要研究方向为惯性导航系统设计、组合导航算法。

E-mail:zhangldxd@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160602.1529.010.html