Underlay认知无线电网络功率与允入控制优化算法
2016-10-18任晓岳陈长兴
任晓岳, 陈长兴
(空军工程大学理学院, 陕西 西安 710000)
Underlay认知无线电网络功率与允入控制优化算法
任晓岳, 陈长兴
(空军工程大学理学院, 陕西 西安 710000)
研究了衬底式(Underlay)频谱共享认知无线电网络中允入控制算法对系统总吞吐量、总传输概率及认知用户中断概率的影响,并提出两种新功率与允入控制联合优化算法。所提算法基于信干噪比与功率对应关系,引入有效信干噪比、有效链路增益比两个新权值。在非可行系统中依据新权值逐步移除违规认知用户,使允入认知用户数目最大化并有效控制总传输功率。在可行系统中利用新权值将“极大—极小”服务质量和总吞吐量优化两个问题转化为易解决的传统线性规划问题。仿真实验结果表明,新算法复杂度低、用户中断概率小且系统吞吐量大。
频谱共享; 允入控制; 中断概率; 总吞吐量
0 引 言
无线频谱资源紧缺已成为制约无线通信技术服务进一步发展的瓶颈。认知无线电技术对授权频谱“二次利用”成为近年来提升频谱资源利用率的一个重要研究方向[1-5]。随着对认知技术深入研究,频谱共享方面获得了一定的研究成果[4-15]。综合频谱共享方面主要研究可知理论上衬底式频谱共享比覆盖式频谱共享的频谱利用率更高,但现有算法仍存在不足。文献[9]提出利用天线阵列达到最小化链路总传输功率目的的分布式算法,但主用户被允许提高传输功率的有效限度未能给出。文献[10]提出一种最大化允入控制算法,在满足单一主用户服务质量要求基础上最大化允入认知用户数量,但该算法将主用户的传输功率等级设为固定值,实用性存在缺陷且计算复杂度较高。文献[11]采用集中随机搜索算法来最大化允入认知用户数量,但该算法的复杂性随着网络中认知用户数量的增多而大幅增加。文献[12]假设所有认知用户的允入门限信干躁比(signal to interference plus noise power ratio, SINR)要求一致,根据链路增益比将认知用户分类,通过二分搜索算法将不符合要求的认知用户移除,虽然有效降低了算法复杂度,但在认知用户允入门限SINR不一致时,算法复杂度依然很高。文献[13]提出基于链路增益比算法,其复杂度得到大幅降低,但其仅适用于允入门限SINR统一的认知网络,难以适应用户应用服务需求的多样性。文献[14]借鉴文献[11]改进得到一种逐步消除算法,将超过最大干扰限度的认知用户移除,降低了不同允入门限SINR时的算法复杂度。文献[15]研究的最大化吞吐量优化算法,在控制认知用户接入以满足主用户服务质量方面是一个非确定行多项式困难问题,需要对所有可能接入的认知用户进行彻底搜索,因此对于大型认知无线电网络并不适用。
本文针对上述研究存在的不足,提出复杂性更低且适应性更强的功率与允入控制联合优化集中式算法。依据用户SINR与功率之间的简单对应关系,引入两个新的允入权值,通过新权值可降低给定SINR的系统可行性检测复杂度。对于可行系统,在保证主用户服务质量基础上为认知用户分配一个高于最低允入门限的SINR,达到最大化系统吞吐量的目的。根据建立的对应关系可将此寻优问题转化为一个传统线性规划问题。对于不可行系统(所有用户的最小可接受门限不能同时满足),根据建立的对应关系该只需移除最少量的认知用户,从而大大降低算法检索的复杂度。
1 系统模型与复杂度分析
1.1“P↔SINR”模型
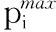
用户i相对于基站的SINR值si对于任何给定功率向量P,均存在以下关系:
(1)
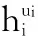
(2)
式中,I表示N×N的单位矩阵;
(3)
1.2系统优化模型
1.2.1联合优化模型
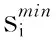
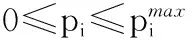
(4)
相应地,用OS(P)表示认知用户中断概率。
(5)
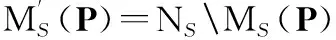
对于一个给定的门限SINR向量Smin,它需要通过“P↔SINR”关系获得一个功率向量P∈[0,Pmax],该功率在所有主用户均以门限SINR值工作基础上最大化允入认知用户的数量。该问题亦可以转化为在保证主用户服务质量基础上最小化认知用户中断率的问题,即
(6)
同时必须服从以下条件:
(7a)
(7b)
其中,约束条件式(7a)和式(7b)分别对应决定系统可行性以及主用户服务质量。
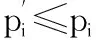
以上问题优化结果并非唯一,存在很多功率矢量满足条件要求。仍需从使认知用户中断概率最小化的传输功率矢量中进一步选取使被支持用户总传输功率最小化的功率矢量,所有允入用户经筛选得到的传输功率恰好可以达到其门限SINR值。由于任意功率矢量P通过式(1)对应一个SINR矢量S,因此该优化筛选过程实质上可称为基于目标函数的SINR分配问题,即
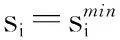
(8)
在此分配问题中,所有主用户以门限SINR值工作并依此获得一个优化可行有效SINR矢量μ*,同时允入和未被允入认知用户分别分配SINR门限值与零值,使允入认知用户数量最大化。
以上式(6)和式(8)优化问题联合执行,经式(8)优化选择得到有效SINR矢量μ*,根据关系式(1)推导出功率矢量P*,P*是经式(6)优化后得到的功率矢量空间P中的最小元素,即优化问题式(6)保证主用户和感知用户的服务质量要求,优化问题式(8)进一步从中筛选优化SINR值分配给认知用户,最终达到最小传输功率最大化允入用户数量的目的。
1.2.2合理性验证
本节将对以上联合优化问题结论中P*为最小元素进行合理性推导证明。
假设:给定一个可行SINR矢量S,φF(S)表示式(3)中矩阵F(S)最大模特征值,由于F(S)中所有的元素都是非负的,根据Perron-Frobenius理论可知,S的可行性促使φF(S)<1,进而式(2)作如下变化:
(9)
对上文的论点此处采用反证法,优化问题(8)的解亦为优化问题(6)的解,因此设P*∈P,若P*不是P中的最小元素,那么必然会存在另外一个P**<≠P*,P**∈P,即至少存在一个认知用户i∈NS拥有以下关系
(10)
此外,P*∈P,P**∈P意味着
(11)
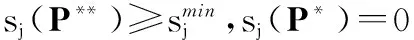
1.3系统可行性检测模型
在以上优化过程(8)中,满足主用户服务质量基础上对认知用户进行允入控制是一个非确定性多项式困难问题,在解决该困难问题方面现有算法大部分是依赖迭代选择AS⊂NS,复杂性较高。同时还需检查对应功率矢量可行性,可行性检查是决定算法复杂度的主要因素。为有效降低整个算法流程复杂度,本文提出一种基于有效SINR矢量μ的低复杂度可行性检测方法,具体模型分析如下:
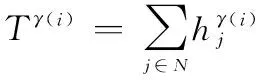
(12)
主用户与认知用户功率可具体分为
(13)
式中,TP,TS分别表示主基站与认知基站收到的总功率(含噪声)。对式(13)进行计算可得
(14)
(15)
(16)
(17)
分别将式(16)代入式(15),式(17)代入式(14)解出TP和TS,将得到的结果进一步代入式(13)最终可得
(18)
式中
因此,对于给定的SINR矢量S,可计算得到其有效SINR矢量μ,对应的功率矢量P通过式(18)计算得到,但其可行性尚需检测。从文献[12]可知,给定门限SINR可行性的检测需要进行矩阵求逆,其复杂度可达到O(N3)。此外,对于非可行门限SINRS并未给出一个支持最大化允入认知用户数目的初始分类移除候选名单。鉴于以上缺陷问题,下面将提出一个基于有效SINR矢量μ的约束条件来完成可行性检测。

(19)
(20)
式中
(21)
(22)
(23)
(24)
(25)
对以上“当且仅当”的论点做证明分析,将式(19)、式(20)各项因素代入,两式成立时μ的可行性可直接解出证明。下面主要介绍当μ可行时,式(19)、式(20)的成立情况。
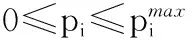
(26)
同理,若0≤pi(i∈NS)成立,则通过式(18)和式(15)可以得到
(27)
通过式(18)、式(26)和式(27)推断可知:当0≤pi, i∈N时,
(28)
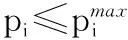
(29)
经式(28)、式(29)不等式联合,并将属于AS的关系因素全部代入不等式(29)右侧,将其他关系因素代入不等式(29)左侧可推知:当μ可行时,式(19)成立。
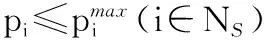
(30)
经式(28)、式(30)不等式联合并将属于AS的关系因素全部代入不等式(30)右侧,将其他关系因素代入不等式(30)左侧可推知:当μ可行时,式(20)成立。
上文提出的“当且仅当”可行性判断只需检测以下两个条件:
条件 1式(19)需成立,为主用户的服务质量提供保障,允入认知用户的影响在可接受范围内,不会造成主用户的服务中断。
条件 2式(20)需成立,保证分配给各允入认知用户的SINR值足以支持其正常工作。
只要给定的有效SINR矢量μ满足上述两条件即可保证其可行性,大大降低了检测复杂度。式(8)提出的优化问题可以等价于在服从约束条件式(19)和式(20)情况以下的允入控制问题:
(31)
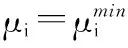
1.4干扰温度限制模型
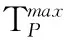
(32)
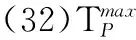
(33)
由此,干扰温度限制值可通过式(34)获得
(34)
2 算法实现
2.1非可行系统功率和允入控制联合算法
上文提出的可行性检测方法在满足保护主用户正常工作基础上,解决了最大化允入用户的问题。继而本节首先提出一种基于主用户保护的有效认知用户逐步移除算法,其算法复杂度与工作性能指标明显优于现有算法。同时为进一步降低算法复杂度,本文又提出一种基于有效链路增益比移除算法,该算法可进一步降低算法复杂度,但需牺牲部分工作性能。实际上这两种算法均依据功率与允入控制联合实现。
2.1.1有效认知用户逐步移除算法实现
在可行判决条件式(19)、式(20)不成立时,该算法将引起最大程度非可行性的认知用户移出允入用户集合,直到所有主用户达到门限SINR值以及剩余允入认知用户均可行为止。实现过程如下。
步骤 1初始化
步骤 1.1假设所有认知用户均分配门限SINR值,主用户亦分配其门限SINR值。
步骤 1.2分别根据式(22)和式(25)估算KP(μNP)和KS(μNP)。
步骤 2允入控制
步骤 2.1若式(19)或式(20)不成立,同时有|AS|>0,则继续按序运行下去,否则转向步骤2.2。
步骤 3功率估计
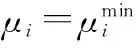
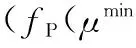
2.1.2基于有效链路增益比算法实现
上述算法已有效降低了复杂度,然而随着认知无线电网络的增大,进一步降低算法复杂度显得十分必要。本节提出一种通过牺牲少量工作性能,进一步降低复杂度的有效链路增益比功率与允入控制联合算法。具体分析如下:
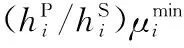
步骤 1初始化
假设所有认知用户都分配了门限SINR值,主用户亦分配了其门限SINR值。
步骤 2接入控制
步骤 2.1若式(19)或式(20)不成立且|AS|>0,继续步骤2.2,否则转向步骤3。
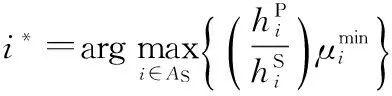
步骤 3功率估计
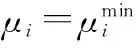
2.1.3算法的全局最优解
在某些特殊情况下,本文提出的算法可获得式(8)中最小中断优化问题的全局最优解。
在所有认知用户拥有相同的目标SINR Smin基础上,具体可分为以下两种特殊情况:
情况 1若式(20)成立适用于AS=NS,则两个算法均可获得认知用户最小中断概率全局最优解。
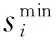
由于在情况1中已假设式(20)成立适用于AS=NS,从上文假设可知,如果式(21)中存在fS(μAS)≤KS(μNP),则可行性成立。
(35)
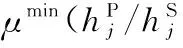
(36)
(37)
从上述式(36)和式(37)中可知:
(38)
因此可以推断允入认知用户集合NS(n*)均达到门限SINR值,假设从上述两算法中获得的允入认知用户数目为n。算法从移除第一个认知用户至剩余n个认知用户可以正常工作为止,从中可推断有n≥n*,前面已有假定n*为最大允入认知用户数目,因此存在结论n=n*。
证毕
情况 2若主基站与认知处于同一位置,有效认知用户逐步移除算法可获得认知用户最小中断概率全局最优解。
(39)
(40)
另一方面,在第2.1.1节算法中存在以下关系:
(41)
(42)
通过上述式(39)~式(42)可知允入认知用户集合μNS(n*)的门限SINR值均可达到。假设通过第2.1.1节算法获得n个允入认知用户,算法从移除第一个认知用户至剩余n个认知用户可以正常工作为止,从中可推断有n≥n*,前面已有假定n*为最大允入认知用户数目,因此存在结论n=n*。
综上所述,若所有认知用户具有相同的门限SINR值,第1种特殊情况表示最初所有认知用户均被允许接入,但对主用户造成的影响超过干扰温度限制,即判决条件(20)成立,式(19)并未成立,在这种情况下一部分主用户可能获得不了其门限SINR值,只需移除最少数量的认知用户直到所有主用户获得其门限SINR值。同样地,第2种特殊情况保证了当主基站和认知基站位于同一地点时,第2.1.1节算法只需移除最少数量的认知用户即可。在这两种特殊情况下,提出的两种算法可得到中断概率最小化问题的全局最优解。
2.1.4算法复杂度分析
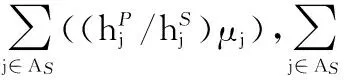
2.2可行系统吞吐量最优化
若系统可行,所有认知用户不会给主用户产生中断影响,均被允许接入网络。在这个情况下,本文所提算法导致的认知用户中断概率为零(所有用户均可接入工作)。然而,可行系统中认知用户可能达到比其门限SINR值更高的SINR值(门限SINR值为最小化值),这样可获得更高的数据传输效率,或者通过增大吞吐量进一步提高认知用户的服务质量。那么可以用用户i的吞吐量Ti作为服务质量的测量。Ti一般为关于si递增凹函数,假设Ti为用户i与其对应接受者之间的链路信道容量,单位为bit/s,具体可表示如下:
(43)
式中,k为常数。
现有大部分关于功率控制系统吞吐量最优化问题,均以变量P的非线性凸优化问题形式提出。本文通过式(18)可以推导出可行系统中有效SINR矢量μ与对应功率矢量P之间的关系,可以将P的非线性凸优化问题转化为关于变量μ的线性规划问题,从而使解决认知用户服务质量和总吞吐量提升的优化问题更加简单易行。
2.2.1认知用户服务质量优化问题
在无线认知网路中,满足用户零中断率基础上,使所有用户至少以其最小可接受门限SINR值工作,最大化认知用户可实现的吞吐量极小值,即为“极大—极小”优化问题:
(44)
同时必须服从以下条件:
(45)
(46)
(47)
当系统可行时,式(44)的优化解相当于给认知用户尽可能高的分配SINR值,即在所有主用户被一直保护的同时最大化认知用户的服务质量。从式(2)或式(18)可知,可行性约束条件(47)是一个关于S的非线性函数。下面将以上问题等效改写成关于变量μ的线性约束。
(48)
同时,必须服从以下条件:
(49)
(50)
(51)
式中
(52)
(53)
(54)
(55)
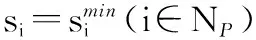
式(44)的目标函数可以等效改写为
(56)
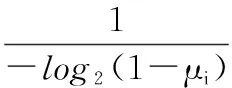
(57)
利用一个辅助变量t,式(44)所提问题可以改写为
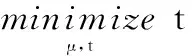
(58)
同时必须满足以下条件:
(58a)
(58b)
(58c)
(58d)
显而易见,以上优化问题为线性规划,解决该问题相对较为简单。
2.2.2最大化吞吐量优化问题
在保证用户零中断率的基础上实现认知用户总吞吐量最大化可以写为以下优化问题:
(59)
同时必须服从以下条件:
(59a)
(59b)
(59c)
同样,该优化问题可以转换为以下优化问题:
(60)
同时必须服从以下条件:
(60a)
(60b)
(60c)
服从条件均为线性凸函数,目标函数为凹函数。假设si≪1, i∈NS,目标函数线性逼近,将优化问题进一步改写为
(61)
同时必须服从以下条件:
(61a)
(61b)
(61c)
以上优化问题为线性规划,可以轻松解决。
3 实验仿真
第2.1.4节中已分析出本文所提两种算法的复杂度,现将其与其他允入控制算法进行制表对比。表1中算法复杂度均来自已有文献且本文对每个算法复杂度均已进行验证。

表1 算法复杂度
从表1中可以看出,本文所提出基于主用户保护条件的有效认知用户逐步移除算法(第2.1.1节算法)与有效链路增益比移除算法(第2.1.2节算法)在实现复杂度方面要优于其他现有算法。其中有效链路增益比移除算法(下文简称算法Ⅲ)的复杂度要低于有效认知用户逐步移除算法(下文简称算法Ⅳ)。
为进一步验证本文所提算法在认知无线电网络中的工作性能优越性,本节设计两组与现有相关算法的仿真对比实验。
仿真实验1,非可行系统中基于不同认知用户数量、不同门限SINR值及不同基站间距离的认知用户最小中断概率和总传输功率对比。
仿真实验2,可行系统中总吞吐量优化对比。
对比对象选取现有算法中复杂度较低、工作性能较为优秀的链路增益比算法(下文简称算法Ⅰ)[13]及最大干扰逐步移除算法(下文简称算法Ⅱ)[14]。具体参数设置如表2所示。

表2 仿真参数设置
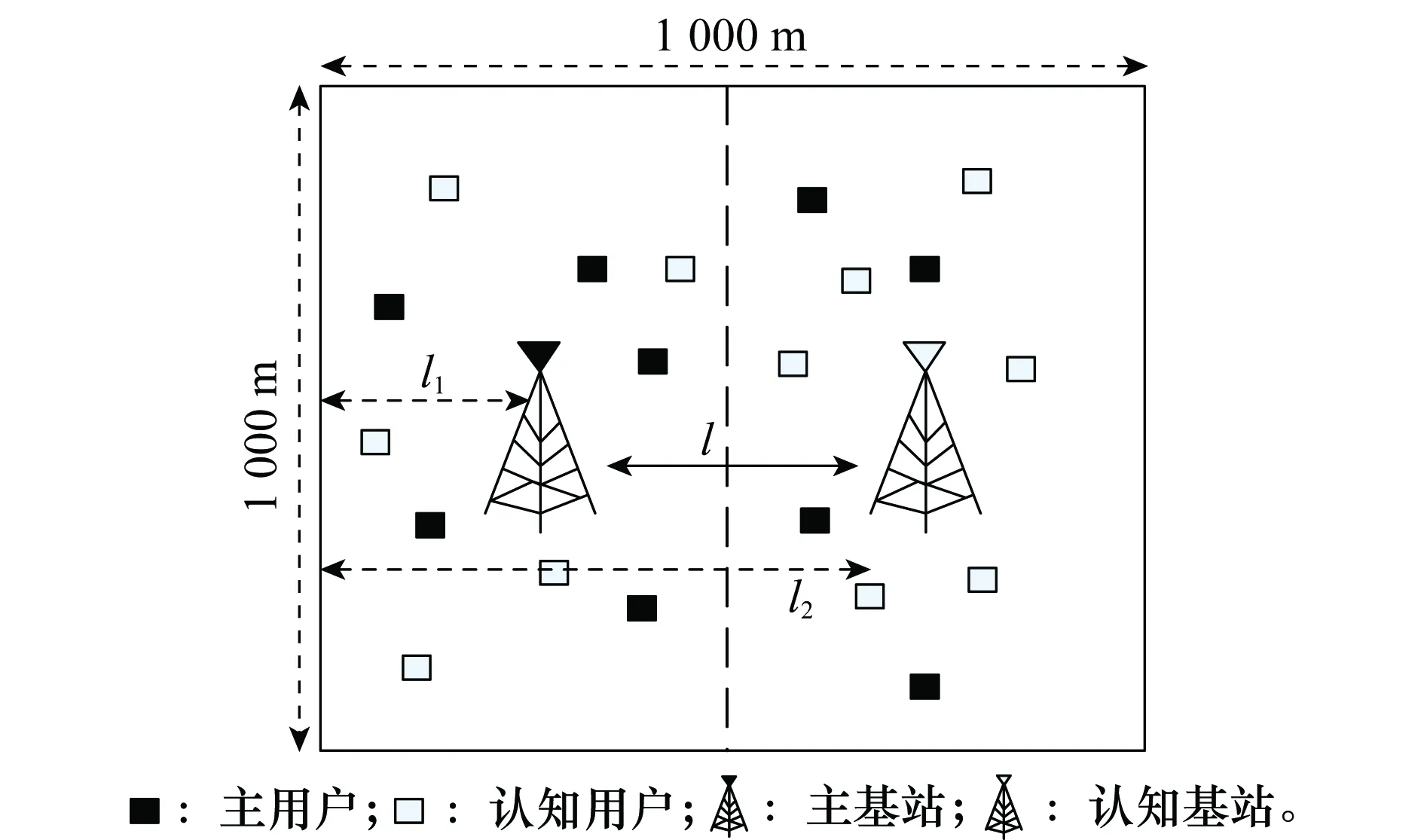
图1 用户及基站分布图Fig.1 Distribution of users and base stations
3.1仿真实验1
3.1.1基于不同认知用户数量的算法性能对比
假设主用户数量为20,认知用户数量从10依次增加至35,用户随机分布在主、认知基站覆盖范围内(1 km×1 km),主用户门限SINR值设定为-18 dB,认知用户门限SINR值从{-14,-18,-22}dB中随机选取。图2、图3为基于不同认知用户数量情况下,4种算法的平均中断概率和平均总传输功率。
从图2和图3中明显可以看出,本文提出的算法Ⅲ和算法Ⅳ在认知用户中断概率和总传输功率方面均优于现有算法Ⅰ和算法Ⅱ。本文提出的算法Ⅲ和算法Ⅳ不仅可以支持更多认知用户允入工作,而且认知用户达到其门限SINR值时总传输功率更低。算法Ⅲ虽然较算法Ⅳ拥有复杂度上的优势,但在中断概率方面却略有差距。例如,在30个认知用户存在的情况下,算法Ⅰ至算法Ⅳ的平均中断概率分别为0.34、0.44、0.31、0.28,因此在认知用户允入数量方面,算法Ⅳ比算法Ⅰ和算法Ⅱ分别提高了18%和百分之36%,算法Ⅲ比算法Ⅰ和算法Ⅱ分别提高了9%和百分之30%。在认知用户总传输功率控制方面,本文提出的算法Ⅳ要略优于算法Ⅲ,随着认知用户数量增大二者差距呈减小趋势。
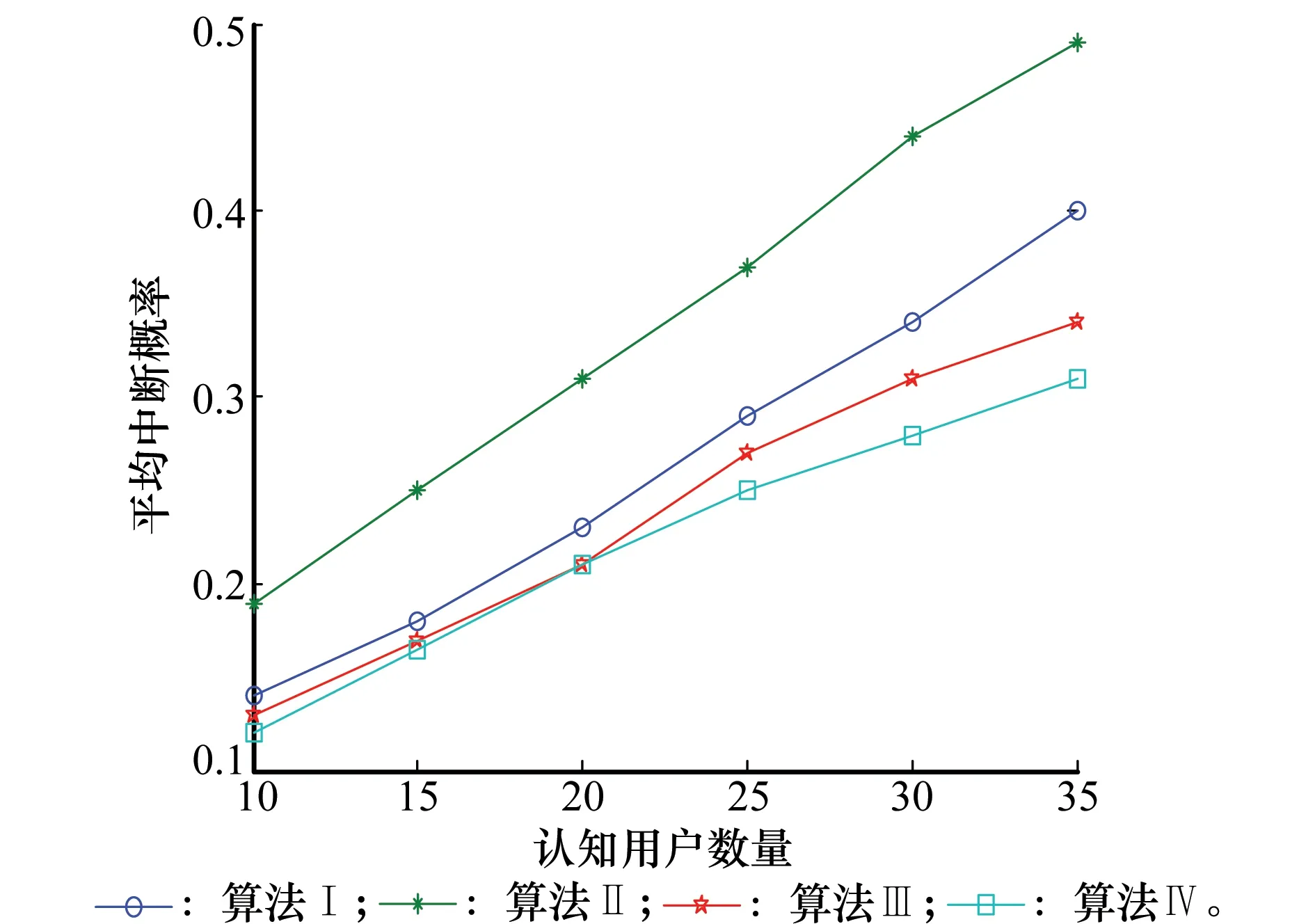
图2 基于不同认知用户数量的中断概率Fig.2 Outage ratio based on the different number of cognitive users
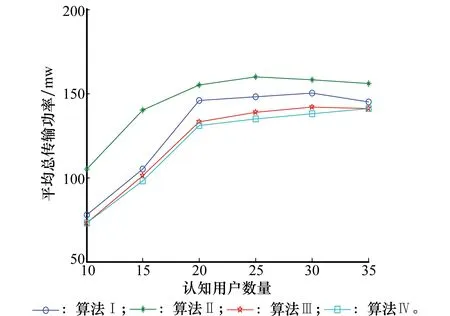
图3 基于不同认知用户数量的总传输功率Fig.3 Aggregate transmit power based on the different number of cognitive users
3.1.2基于用户不同门限SINR的算法性能对比
假设主用户数量20,认知用户数量35,基站间距离为100 m,主用户门限SINR值为-18 dB,每个认知用户被随机分配门限SINR值Smin或Smin-10 dB,其中门限Smin以1 dB跨度从-14~-22 dB变化。图4、图5为各算法基于不同门限SINR值的的认用户中断概率和总传输功率。
从图4中可以明显看出,本文提出的算法Ⅲ和算法Ⅳ认知用户平均中断概率要优于现有算法Ⅱ,同时随着门限SINR值的增大,二者较现有算法Ⅰ的中断概率优势逐渐明显。从图5中可以看出,在认知用户总传输功率方面,随着认知用户门限SINR值的提高本文提出的算法Ⅲ和Ⅳ并不能全程保持控制传输功率更小化,有待进一步改进提高,但综合考虑仍具有一定优势。
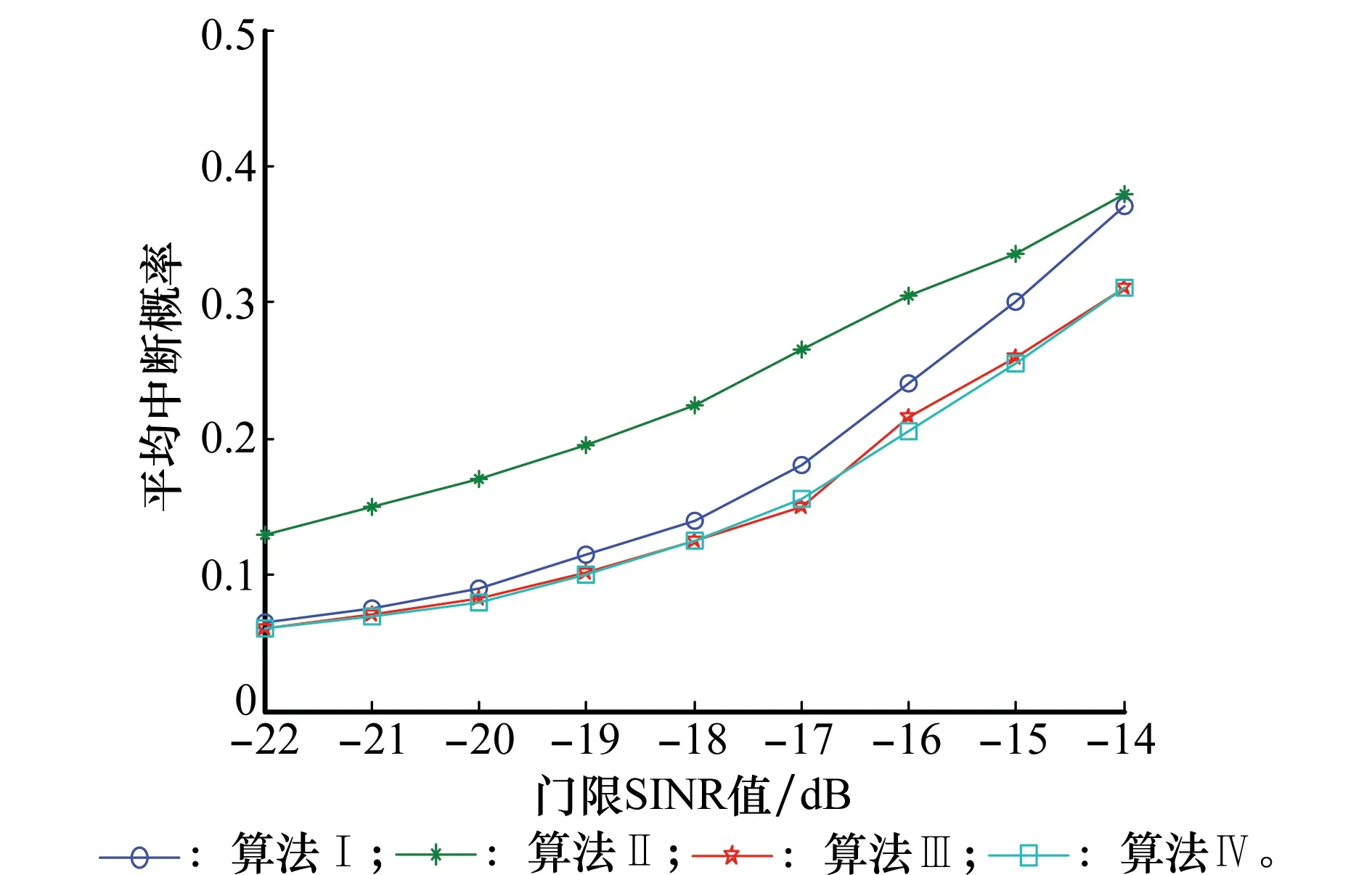
图4 基于不同认知门限SINR的中断概率Fig.4 Outage ratio based on the different target SINR
3.1.3基于基站间不同距离的算法性能对比
为评测主、认知基站间不同距离对4种算法性能带来的影响,假设主用户数量20,认知用户数量35,主用户门限SINR值为-18 dB,认知用户门限SINR值从{-14,-18,-22}dB中随机选取,用户随机分布在覆盖范围内,将基站间距离以跨度40 m从0~160 m变化。
从图6中可以明显看出,虽然本文提出的两种算法认知用户平均中断概率随着基站间距离增大而提升,但其对应距离上仍小于现有算法Ⅰ和算法Ⅱ。从图7可以明显看出,在总传输功率方面,80 m范围内本文算法Ⅲ和算法Ⅳ性能介于现有算法Ⅰ和算法Ⅱ之间,随着基站间距离的增大,本文算法的性能优势逐渐显现。
综上分析可得,非可行系统中本文提出的算法在认知用户数量较多、基站距离较大及门限SINR值较小时性能优势明显。
3.2仿真实验2
该组仿真实验中假设系统可行,对比分析本文提出的“极大—极小”服务质量和最大化吞吐量优化问题对系统总吞吐量的提升。实验参数设置主用户数量为5,认知用户数量以5跨度从5递增至25,主用户门限SINR值为-18 dB,认知用户从最小可接受门限SINR值-22 dB或-18 dB中选取,用户随机分布在覆盖范围内,基站间距离为100 m。
从图8可以明显看出,采用“极大—极小”服务质量和最大化吞吐量优化方法,相比于直接为认知用户分配最小可接受门限SINR值,能够大量提升总吞吐量,随着认知用户的增加,由于干扰限制问题,两种优化问题均出现总吞吐量下降,但总体上优势明显。从图9可以看出,在对应相同认知用户基础上,本文两个优化问题对总传输功率的控制也要优于直接分配最小门限SINR值的方法。
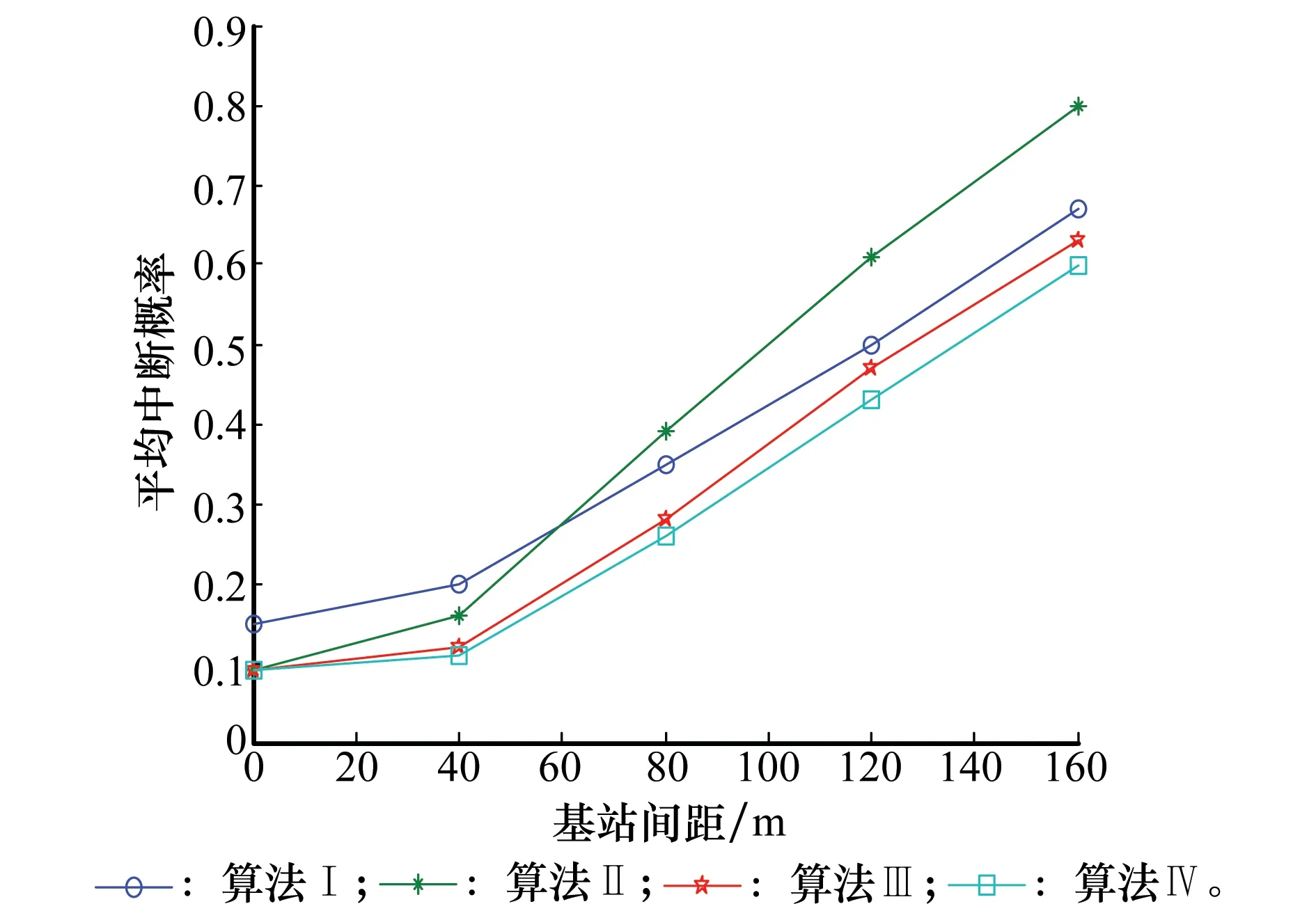
图6 基于基站不同间距的中断概率Fig.6 Outage ratio based on the different distance between the base stations
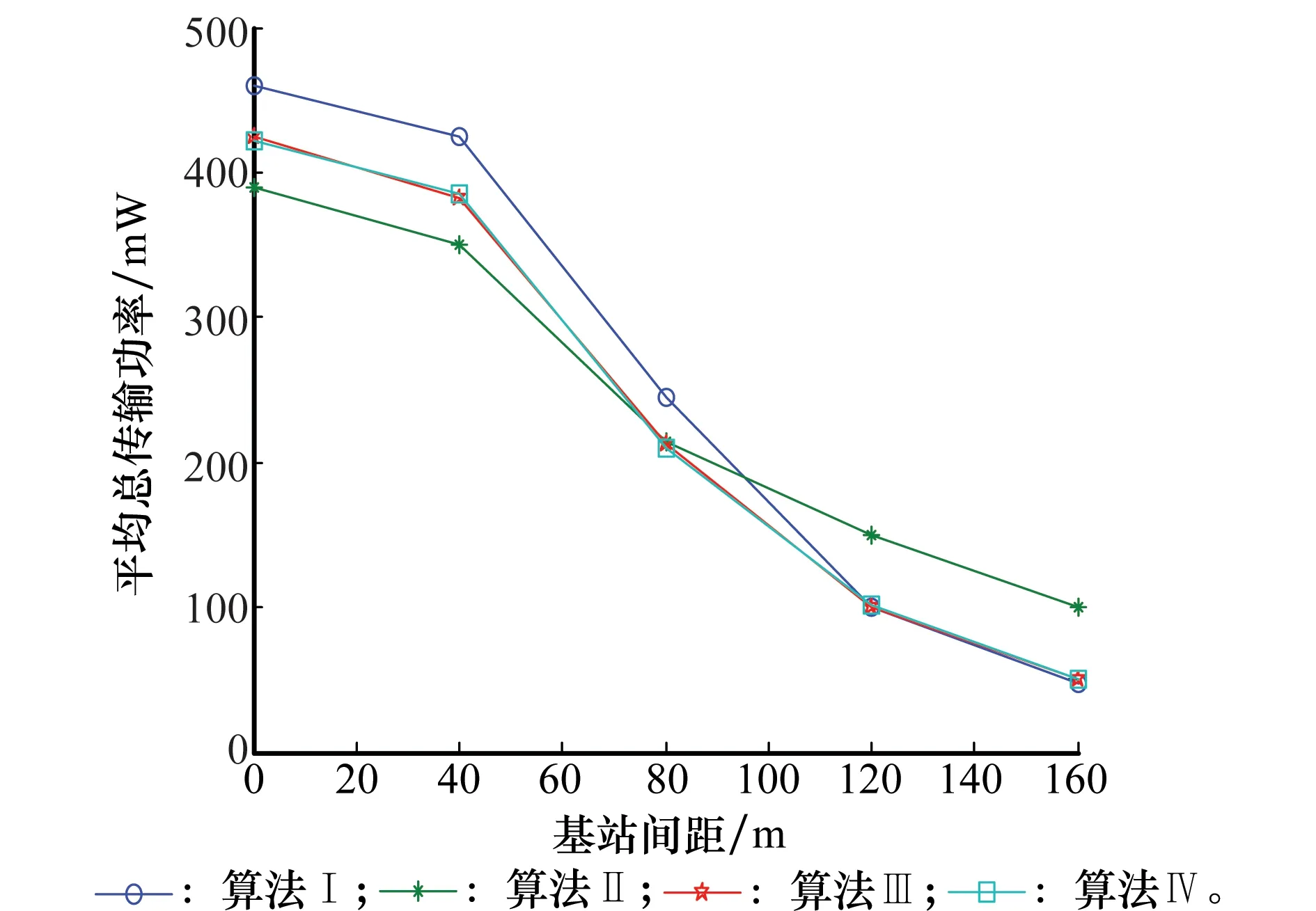
图7 基于不同基站间距的总传输功率Fig.7 Aggregate transmit power based on the different distance between the base stations
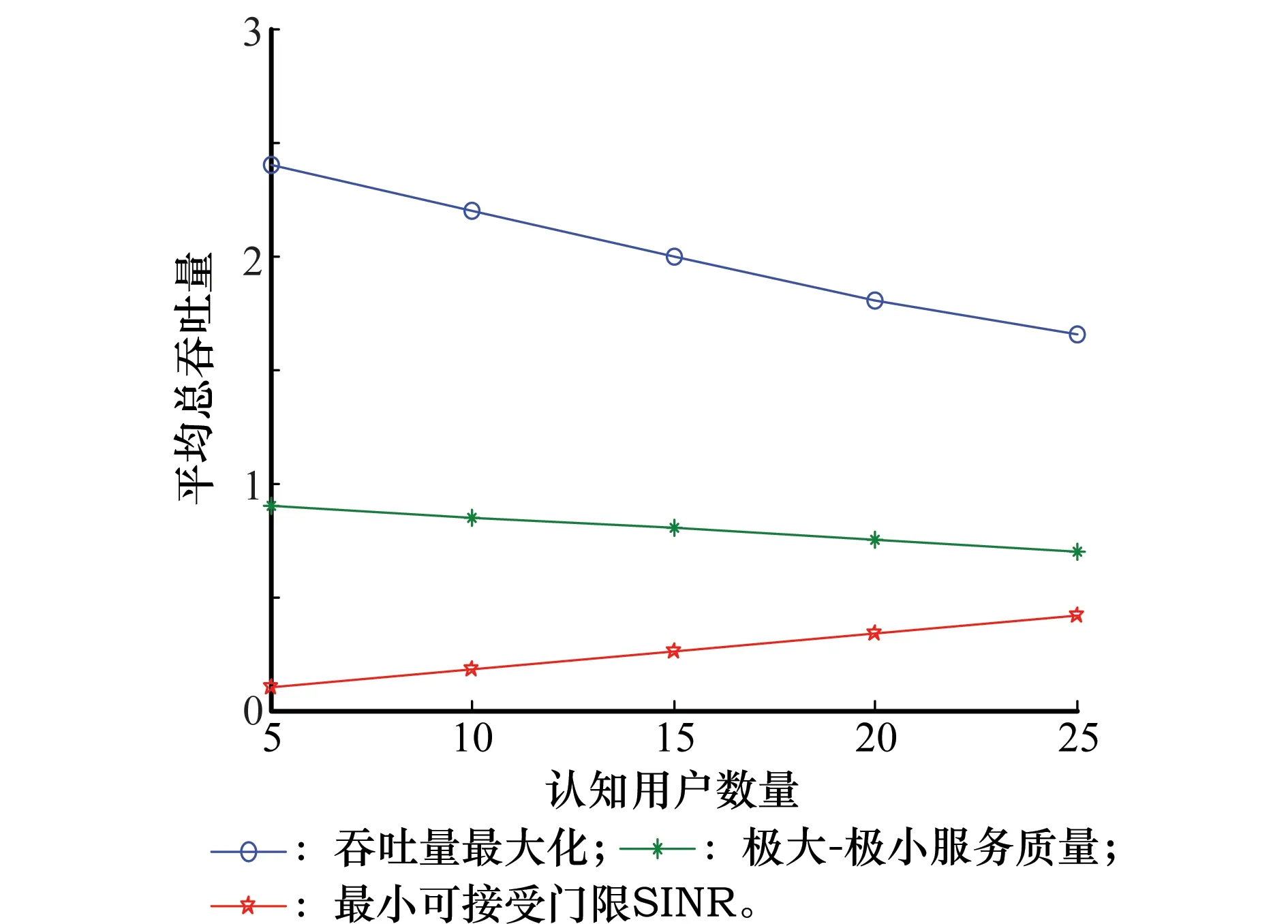
图8 基于不同认知用户数量的总吞吐量Fig.8 Aggregate throughput based on the different number of cognitive users
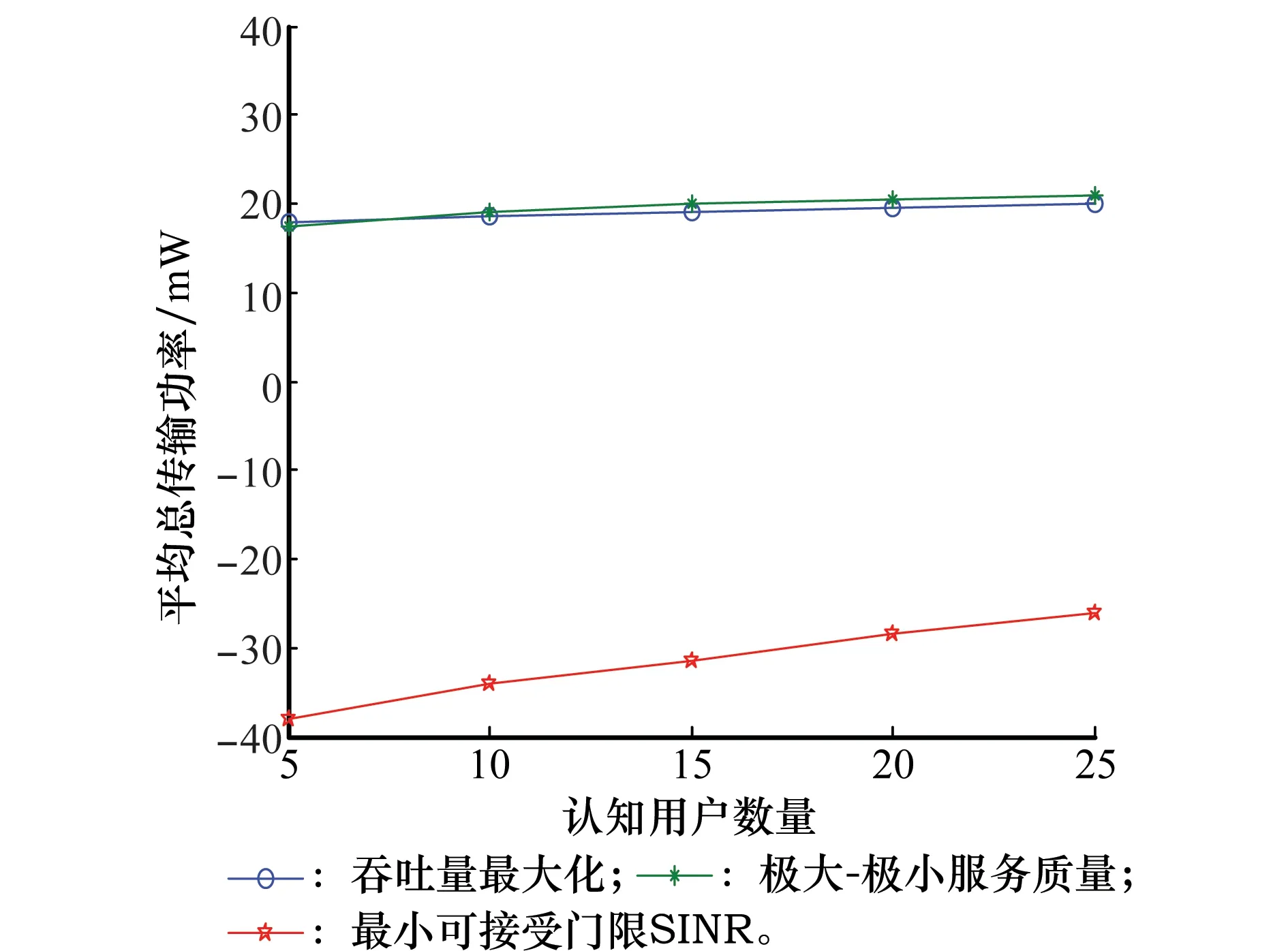
图9 基于不同认知用户数量的总传输功率Fig.9 Aggregate transmit power based on the different number of cognitive users
4 总结分析
本文研究了Underlay认知无线电网络中基于功率与允入控制联合的频谱共享优化问题。本文首先简单推导了“P↔SINR”模型,引入有效SINR和有效链路增益比两个新权值,然后基于此关系模型提出两种功率和允入控制联合集中算法,两个算法可以在保证主用户正常工作情况下移除最少数量的认知用户,与现有算法相比不仅有效降低了认知用户中断概率还有效降低了算法复杂度。同时基于“P↔SINR”模型进一步将“极大—极小”服务质量和最大化吞吐量两个非线性凸优化问题转化为易于解决的传统线性规划问题,在可行系统总吞吐量方面优化效果明显。
[1] Yin C, Tan X Z, Ma L. Global proportional fairness scheduling algorithm based on spectrum aggregation in cognitive radio[J].ActaPhysicaSinica, 2014, 63(11):1-4.(殷聪,谭学治,马琳. 认知无线电中基于频谱聚合的全局比例公平调度算法[J]. 物理学报,2014, 63(11):1-4.)
[2] Monemi M, Asli A R Z, Haghighi S G, Ra-sti M. Distributed multiple target-SINRs track-ing power control in wireless networks[J].IEEETrans.onWirelessCommunications,2013,12(4):1850-1859.
[3] Zhang X J, Lu Y, Tian F. Double threshold cooperative spectrum sensing for cognitive radio based on trust[J].ActaPhysicaSinica, 2014, 63(7): 11-16.(张学军,鲁友,田峰. 基于信任度的双门限协作频谱感知算法[J]. 物理学报,2014, 63(7):11-16.)
[4] Rasti M, Hossain E. Distributed priority based power and admission control in sellular wireless networks[J].IEEETrans.onWirelessCommunications, 2013, 12(9):4483-4495.
[5] Liu Y, Peng Q Z, Shao H Z. A novel spectrum detecting algorithm for cognitive radio based on the characteristics of authorized channel[J].ActaPhysicaSinica, 2013, 62(7):3-6.(刘允,彭启宗,邵怀宗. 一种基于授权信道特性的认知无线电频谱检测算法[J]. 物理学报,2013, 62(7):3-6.)
[6] Zhang J C, Fu N, Qiao L Y. Investigation of information bandwidth oriented spectrum sensing method[J].ActaPhysicaSinica, 2014, 63(3):11-15.(张京超,付宁,乔立岩. 一种面向信息带宽的频谱感知方法研究[J]. 物理学报,2014, 63(3):11-15.)
[7] Zhang Q, Liu G B, Yu Z Y, et al. An adaptive global optimization algorithm of cooperative spectrum sensing with relay[J].ActaPhysicaSinica, 2015, 64(1):41-45.(张茜,刘光斌,余志勇. 一种面向中继协作频谱感知系统的自适应全局最优化算法[J]. 物理学报,2015, 64(1):41-45.)
[8] Niu D Z, Chen C X, Ren X Y. Blind angle elimination method in weak signal detection with Duffing oscillator and construction of detection statistics[J].ActaPhysicaSinica, 2015, 64(6):33-37.(牛德志,陈长兴,任晓岳. Duffing振子微弱信号检测盲区消除及检测统计量构造[J]. 物理学报,2015, 64(6):33-37.)
[9] Islam M H, Liang Y C, Hoang A T. Distributed power and admission control for cognitive radio networks using antenna arrays[C]∥Proc.oftheIEEEInternationalSymposiumonDynamicSpectrumAccessNetworks, 2007:3250-3253.
[10] Mitliagkas I, Sidiropoulos N D, Swami A. Joint power an admission contrl for ad-hoc and cognitive underlay networks[J].IEEETrans.onWirelessCommunications, 2011,11(12): 4110-4121.
[11] Xing Y, Mathur C N, Haleem M A, et al. Dynamic spectrum, access with QoS and interference temperature constraints[J].IEEETrans.onMobileComputer, 2007, 6(4):423-433.
[12] Le L B, Hossain E. Resource allocation for spectrum underlay in cognitive radio networks[J].IEEETrans.WirelessCommunications, 2008, 7(12):423-436.
[13] Kim D, Le L, Hossain E. Joint rate and power allocation for cognitive radios in dynamic spectrum access environment[J].IEEETrans.onWirelessCommunications, 2008, 7(2):5517-5527.
[14] Qian L, Li X, Attia J, et al. Power control for cognitive radio ad hoc networks[C]∥Proc.oftheIEEEInternationalWorkshoponLocalandMetropolitanAreaNetworks, 2007:1012-1017.
[15] Gu H Y, Yang C Y, Fong B. Low complexity centralized joint power and admission control in cognitive radio networks[J].IEEECommunicationsLetters, 2009, 13(6):420-422.
Optimization algorithms based on power and admission control for underlay cognitive radio networks
REN Xiao-Yue, CHEN Chang-Xing
(School of Science, Air Force Engineering University, Xi’an 710000, China)
An investigation is carried out that the influence of aggregate throughput, aggregate transmit power and outage ratio caused by the admission control algorithm in underlay cognitive radio networks, and two new optimization algorithms for joint power and admission control are proposed. In these algorithms, we introduce two new weights based on the relation between the signal to interference plus noise ratio and transmit power. In the infeasible system, the irregularity cognitive users are gradually removed according to the new weight, it can maximize the number of the access cognitive users and effective control aggregate transmit power can be solved. In the feasible system, we use the new weight to translate the optimization problem of max-min quality of service (QoS) and maximum aggregate throughput into the traditional linear programming problem. Numerical simulations demonstrate that the new algorithm has lower complexity, the lower users outage ratio and larger system aggregate throughput.
spectrum sharing; admission control; outage ratio; aggregate throughput
2015-11-17;
2016-06-12;网络优先出版日期:2016-07-17。
国家安全重大基础研究专题协议(6132660401)资助课题
TN 92
A
10.3969/j.issn.1001-506X.2016.10.25
任晓岳(1989-),男,博士研究生,主要研究方向为认知无线电、卫星导航。
E-mail:776596484@qq.com
陈长兴(1963-),男,教授,博士研究生导师,主要研究方向为电子信息综合化工程。
E-mail:349913314@qq.com
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160717.0949.010.html
