基于组网雷达的空间旋转对称进动目标三维重构

2016-10-18胡晓伟童宁宁王建业丁姗姗赵小茹

系统工程与电子技术 2016年10期

关键词：进动锥体夹角

胡晓伟, 童宁宁, 王建业, 丁姗姗, 赵小茹

(空军工程大学防空反导学院, 陕西西安 710051)

基于组网雷达的空间旋转对称进动目标三维重构

胡晓伟, 童宁宁, 王建业, 丁姗姗, 赵小茹

(空军工程大学防空反导学院, 陕西西安 710051)

对于空间旋转对称进动目标,单部雷达成像仅能获得目标在雷达视线(line of sight,LOS)方向的一个切面,无法反映目标真实的三维结构,同时进动增加了成像的复杂度。利用组网雷达多视角观测的特点,提出一种基于组网雷达的旋转对称进动目标三维重构方法。首先建立了旋转对称进动目标的回波模型;在估计视线-轴线夹角的基础上,采用复数逆投影方法实现进动目标的二维成像,并分析了允许的夹角误差范围;基于分布式雷达二维图像,提出一种适用于旋转对称目标的三维重构方法,通过对各二维图像进行空间定标、匹配融合、强点检测和曲线圆拟合,最终实现目标的三维重构;最后通过仿真实验初步验证了该方法的有效性。

组网雷达; 旋转对称进动目标; 复数逆投影; 三维重构

0　引　言

弹道目标识别是当前弹道导弹中段防御的热点和难点。雷达成像能够提供目标直观的外形和结构特征,是中段目标识别的一个重要手段。进动是弹道中段目标特有的微动形式[1],会导致目标姿态的快速变化,使得以往的匀速小转角成像方法不再适用。同时,弹道目标多为旋转对称结构,目标的自旋运动对回波没有调制,因此单部雷达获得的始终是雷达视线方向上目标一个切面的信息,无法据此重构弹道目标真实的三维空间结构。因此,有必要针对空间旋转对称进动目标的三维重构方法开展研究。

关于空间进动目标二维成像,目前已取得一些研究成果。文献[2]利用窄带雷达实现了空间进动锥体目标的二维成像;文献[3]提出了一种基于后向投影变换的空间进动目标成像新方法;文献[4]将匹配追踪(matching pursuit,MP)稀疏分解引入弹道目标成像,提出了一种弹道中段目标微动逆合成孔径雷达(inverse synthetic aperture radar,ISAR)成像方法;对于空间非旋转对称进动目标,文献[5]基于时频分析技术,研究了旋转对称进动目标的二维成像方法。而目前国内外关于空间进动目标三维成像方面研究还较少[6],现有研究多集中在空间自旋目标的三维成像[7-10]。但已有一些关于进动目标三维特征提取与运动参数估计方面的研究,如文献[11]基于组网雷达研究了有翼弹道目标三维进动特征提取,获得了目标的空间锥旋矢量、进动周期、自旋周期等特征参数;文献[12]在多个雷达站距离像匹配的基础上,重构了锥体弹头各散射点的三维空间位置,并实现了锥体弹头参数的估计;文献[13]提出了一种有翼弹头的进动参数提取方法。

与三维特征与运动参数相比,目标的三维图像能够提供更加直观、更加丰富的目标信息。在文献[11-12]的启发下,本文将研究基于组网雷达的空间旋转对称进动目标的三维重构。组网雷达由空间分布配置的单一体制或混合体制的多部雷达组网而成,可以获得目标更为全面和详细的信息,因而近年来受到极大关注[14]。本文考虑利用分布式宽带雷达组网,以获得目标多角度的二维切片图像,因为其中包含了目标的三维信息,因此有望通过信息的融合处理重构目标真实的三维结构。基于此本文首先建立了空间旋转对称进动目标的回波,研究了适用于空间进动目标的二维成像方法,在此基础上利用组网雷达信息对空间旋转对称目标的三维重构方法进行了研究。

1　空间旋转对称进动目标回波建模

1.1进动模型

理论和实验表明,在高频区,目标总的电磁散射可以用等效散射点模型来近似[15]。对于如图1所示的空间旋转对称锥体目标,其等效散射中心位于锥顶以及雷达视线与目标对称轴所在平面与底部边缘的交点处。其中XYZ为参考坐标系,xyz为目标本地坐标系,y轴为目标对称轴,锥体以Y轴为进动轴作进动。

图1　空间旋转对称锥体进动模型Fig.1　Model of spatial precession targets with rotational symmetry

对于锥顶散射点P0,设其在本地坐标系中的初始位置为lP0,则t时刻在参考坐标系中的位置可表示为

(1)

式中,Rinit为锥体的初始旋转矩阵;Rconing为锥旋旋转矩阵,由Rodrigues[16]公式

(2)

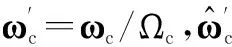
P1,P2为雷达视线(lineofsight,LOS)和对称轴所在平面与锥体底面边缘的交点,其运动规律与目标主体不一致,属于非理想散射点。设锥体质心到底面的距离为d,底面半径为a,则根据锥体底面非理想散射点与雷达视线、锥体结构的空间相对位置关系[16],其位置矢量可表示为

(3)

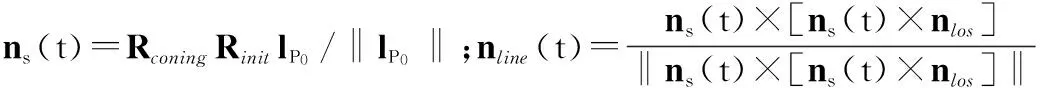
1.2回波模型

设雷达发射线性调频信号:

(4)

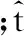
目标回波信号可表示为

(5)

式中,ρ(x,y)和R(x,y;tm)分别为目标上(x,y)处散射点的散射强度和在tm时刻的径向距离。

对回波解线频调处理后,可得距离时间域信号:

(6)

式中，RΔ(x,y;tm)=R(x,y;tm)-Rref；Rref为参考信号参考距离。

2　进动目标的二维复数逆投影成像

2.1二维逆投影成像方法

由式(1)可知,锥顶散射点P0的运动规律为正弦形式,而非理想散射点P1,P2的运动规律与P0不同,除正弦形式外还包含其他高阶调制项[7]。文献[7]通过理论分析证明,当进动角较小时,高阶项对散射点运动形式的调制作用很小,因此P1,P2的运动规律可近似为正弦形式。

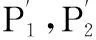
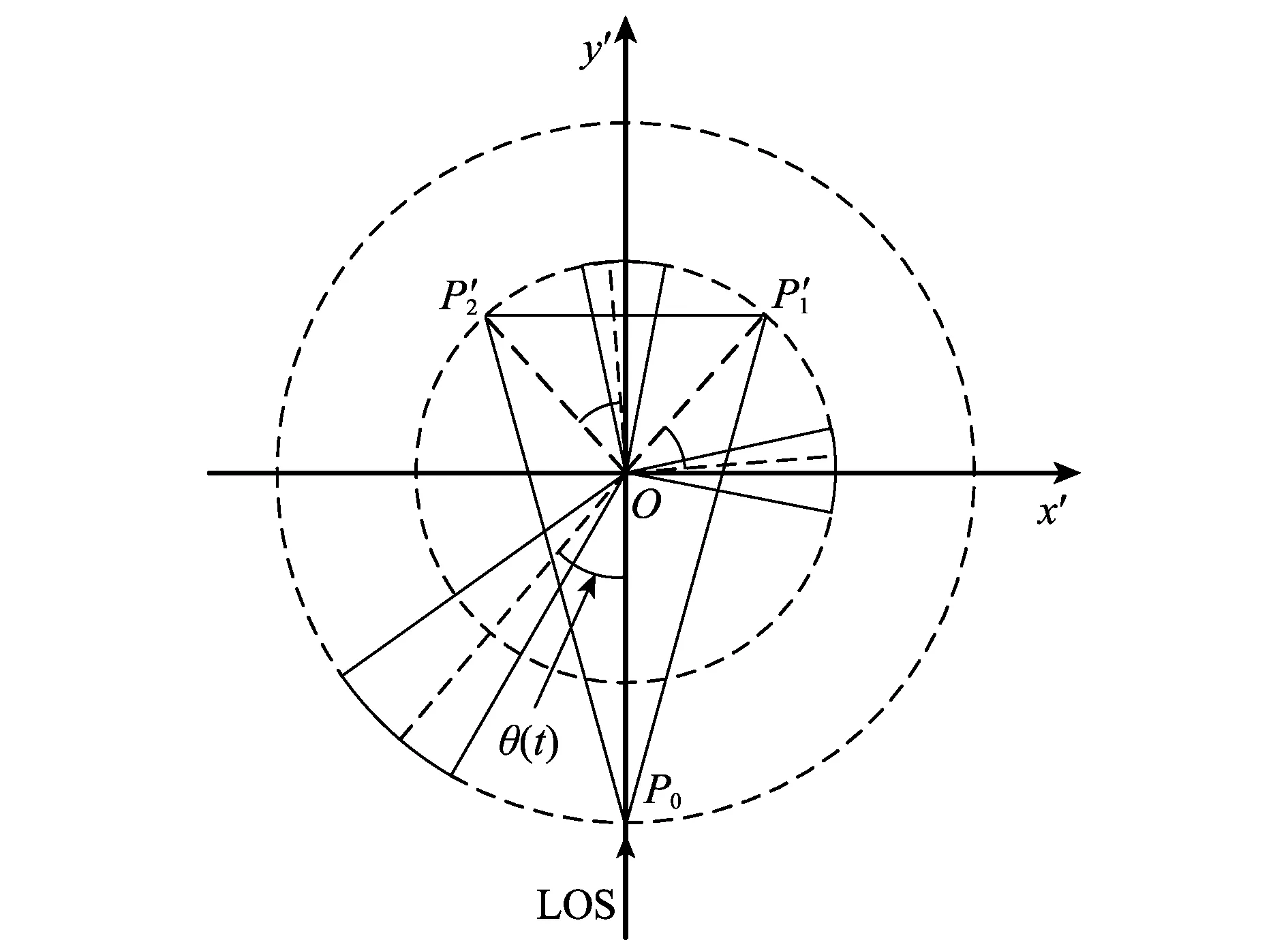
图2　三维进动的等效二维转动示意图Fig.2　Equivalent two-dimensional rotation of three-dimensional precession

对图2中的二维转动目标,有RΔ(x,y;tm)=xsinθ(tm)+ycosθ(tm),则

(7)

对以上二维转动目标,可以利用复数逆投影算法进行二维成像。

(8)

2.2夹角估计方法

式(8)所示投影变换的关键是夹角θ(tm)的估计,下面给出一种基于分布式雷达组网的夹角估计方法。

步骤 1在非理想散射点正弦近似的条件下,可以利用文献[12]方法实现不同雷达站之间散射点的匹配。

步骤 2利用文献[7]的方法分别提取锥顶散射点微动曲线的幅度、均值和频率,进而利用文献[11]的方法解算目标进动轴单位方向矢量。

步骤 3初始位置矢量的解算。

设雷达视线方向单位矢量为nlos,则由式(1)可得,锥顶散射点在雷达视线方向的距离变化可表示为

(9)

(10)

式中，m,μ均可由步骤2得到。则单部雷达观测可以获得关于未知量的2个方程,所以理论上求解l0只需组网中2部雷达的数据,联立以下方程组进行求解即可

(11)

步骤 4夹角估计。夹角θ(tm)可由下式求得

(12)

2.3夹角估计误差分析

从成像过程看,估计的夹角不可避免地会存在误差,从而对成像结果造成影响。下面对成像可承受的误差范围进行分析。

设目标只存在一个强散射点,即

估计的夹角为θ′(tm),则在点(x0,y0)处的投影值为

(13)

其中,Δr=x0(sinθ′(tm)-sinθ(tm))+y0(cosθ′(tm)-cosθ(tm)),令角误差Δθ(tm)=θ′(tm)-θ(tm)(单位：rad),代入Δr,经整理后可得

(14)

当Δθ(tm)很小时,满足cosΔθ(tm)≈1,sinΔθ(tm)≈Δθ(tm),此时

(15)

式中,L为目标在成像平面内的横向最大距离。

由式(13)可知,要实现图像在点(x0,y0)处的有效聚焦,包络和相位[3]需分别满足

(16)

进而可得角误差需满足的条件为

(17)

式中，ρr为雷达的距离分辨率；λ为雷达信号波长。

3　旋转对称目标的三维重构

对于旋转对称目标,单部雷达得到的仅是目标在雷达视线方向上的一个切片图像,无法反映目标的三维结构。分布式雷达网中不同雷达获取的二维图像反映了目标在不同视角下的二维切片,原则上通过融合这些二维切片就有可能真实地重构目标的三维结构。

3.1二维图像的空间定标

以上获取的二维图像实际是三维目标在雷达视线方向上的一个切面,要实现不同二维图像在空间上的融合,首先需要确定二维切面在空间中的位置,即二维图像的空间定标。

切面图像由目标轴线方向和视线方向共同确定。设第i部雷达获取的二维图像为Ii,则Ii在三维空间中的位置可表示为(l0×nlos)·li=0,li为Ii上点的三维坐标。设Ii对应的目标空间三维图像为Ji,则Ji(li)=Ii。

3.2二维图像的空间配准与融合

因为在不同视角下,目标上非理想散射点的位置是变化的,而锥顶散射点的相对位置固定,因此这里以锥顶散射点为基准进行多幅二维图像的配准和融合。

由进动目标二维成像过程可知,目标二维图像的y′轴负方向与锥体对称轴方向重合。因此对不同二维图像进行空间配准时,只需进行空间位置的平移,而不需要进行姿态的调整。

3.3三维重构

对配准融合后的三维图像J,检测除锥顶散射点之外的局部强散射点,并记录各散射点的三维坐标(xl,yl,zl)(l=1,…,m,m为检测到的强点个数)。考虑到目标的旋转对称性,利用三维曲线圆对检测到的散射点进行空间拟合,这样目标的三维重构问题就转化为非线性曲线的拟合问题。三维空间的曲线圆可以表示为

(18)

式中，(x0,y0,z0)为曲线圆心坐标；ρ曲线圆半径；w为曲线圆所在平面的法向单位矢量。式(18)可以转化为关于z的显式形式z=F(A;x,y),其中A=(x0,y0,z0,ρ,w)为参数向量。

应用最小二乘拟合准则,以上三维曲线的拟合问题即等价为求解以下最优化问题

(19)

将取得最优解时的参数向量A带回式(18),便得到锥体底面的重构结果。联合锥顶散射点和锥体底面圆,即可唯一重构锥体目标的三维空间结构。

4　仿真实验

仿真目标为一个进动锥体,长3m,底面半径1m,进动频率1Hz,进动角20°。目标回波产生采用动态电磁仿真的方法,首先用几何绕射理论和物理光学法相结合的静态电磁计算法[6]对锥体目标进行宽带、全方位的雷达散射截面(radarcrosssection,RCS)计算,之后结合第1节的目标进动模型,对静态RCS进行抽取,得到目标的动态电磁仿真回波。雷达网由3部雷达组成,在参考坐标系中的坐标分别为(-707,0,0)km、(-354,0,-612)km、(354,0,-612)km,目标坐标为(0,707,0)km。各雷达发射载频不同的线性调频信号,脉宽1μs,带宽2GHz,脉冲重复频率1 000Hz,假设各雷达同步对目标观测1s。

图3给出了第1部雷达经dechirp处理后的距离时间域信号。提取各部雷达距离曲线的特征,并联合解算目标轴线的初始位置矢量,即可估计各部雷达视线与目标轴线的实时夹角。图4给出了第1部理想情况下的雷达夹角估计结果。

图3　第1部雷达距离时间域信号Fig.3　Range profiles in radar 1

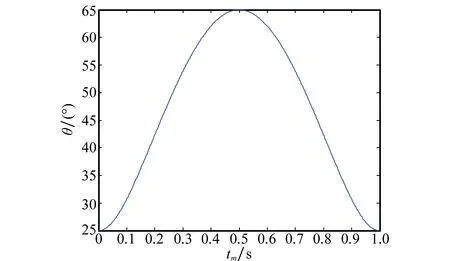
图4　第1部雷达夹角估计值Fig.4　Estimated value of the angle in radar 1

在估计夹角的基础上,利用复数逆投影算法对各部雷达回波进行二维成像。图5为第1部雷达的二维成像结果。

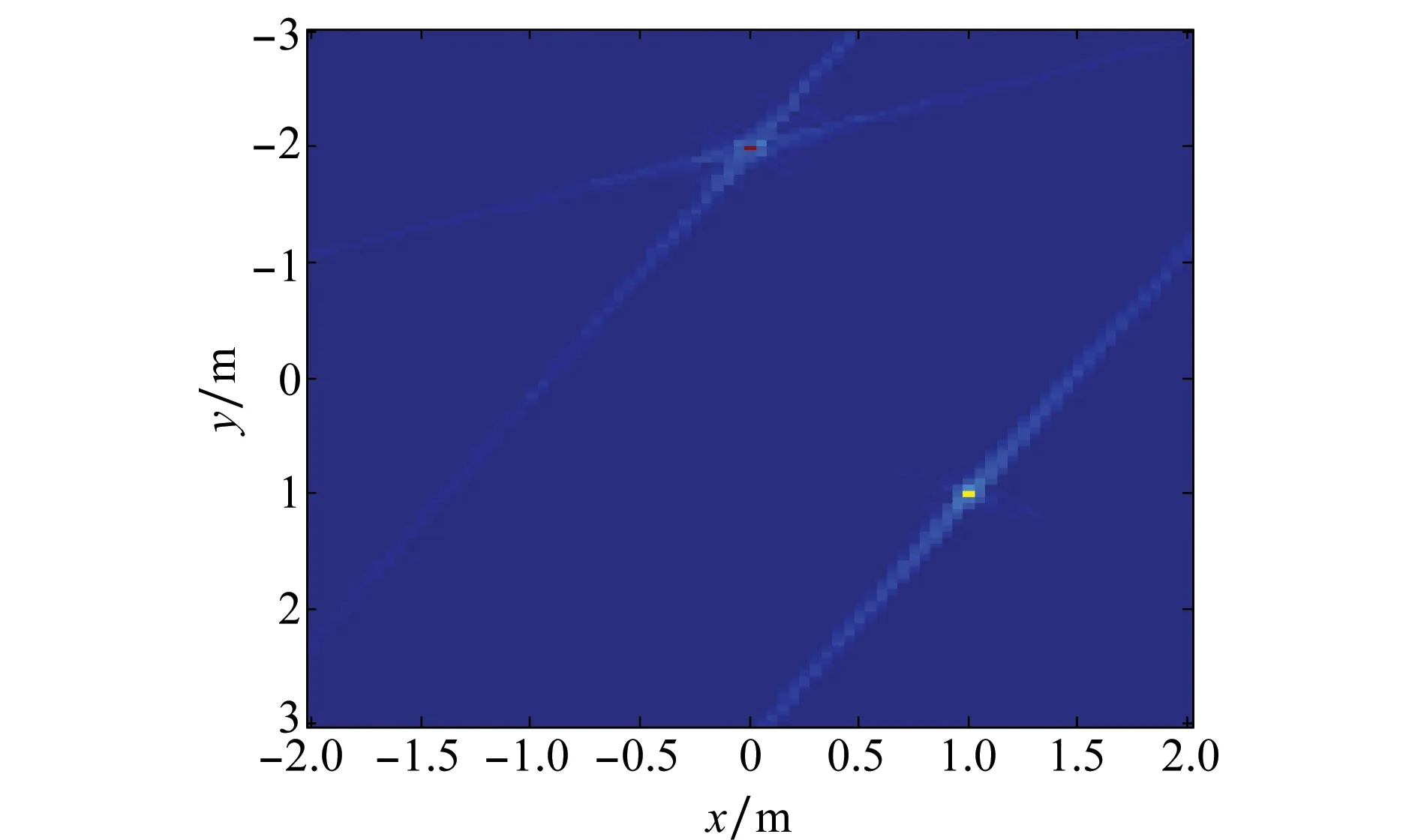
图5　第1部雷达的二维成像结果Fig.5　Two dimensional imaging result in radar 1

考虑估计的夹角不可避免会有误差,为分析其对成像的影响,在理想夹角基础上加入方差为σ2的零均值高斯分布噪声。由式(17)可计算出夹角误差应满足的范围为Δθ(tm)<ΔΘ=0.003 75,图6和图7分别为σ=0.8ΔΘ和σ=2ΔΘ时,第1部雷达的成像结果。

图6　σ=0.8ΔΘ时第1部雷达成像结果Fig.6　Imaging result in radar 1 with σ=0.8ΔΘ

由图6和图7可以看到当σ=0.8ΔΘ时,图像质量下降不明显;而当σ=2ΔΘ时,图像中目标点会发严重散焦。因此,当噪声方差小于ΔΘ2时,通常可保证较好的二维成像效果。

图7　σ=2ΔΘ时第1部雷达成像结果Fig.7　Imaging result in radar 1 with σ=2ΔΘ

对各二维图像进行空间定标、配准和融合后,可以得到目标在空间上的三维切面图,如图8所示。

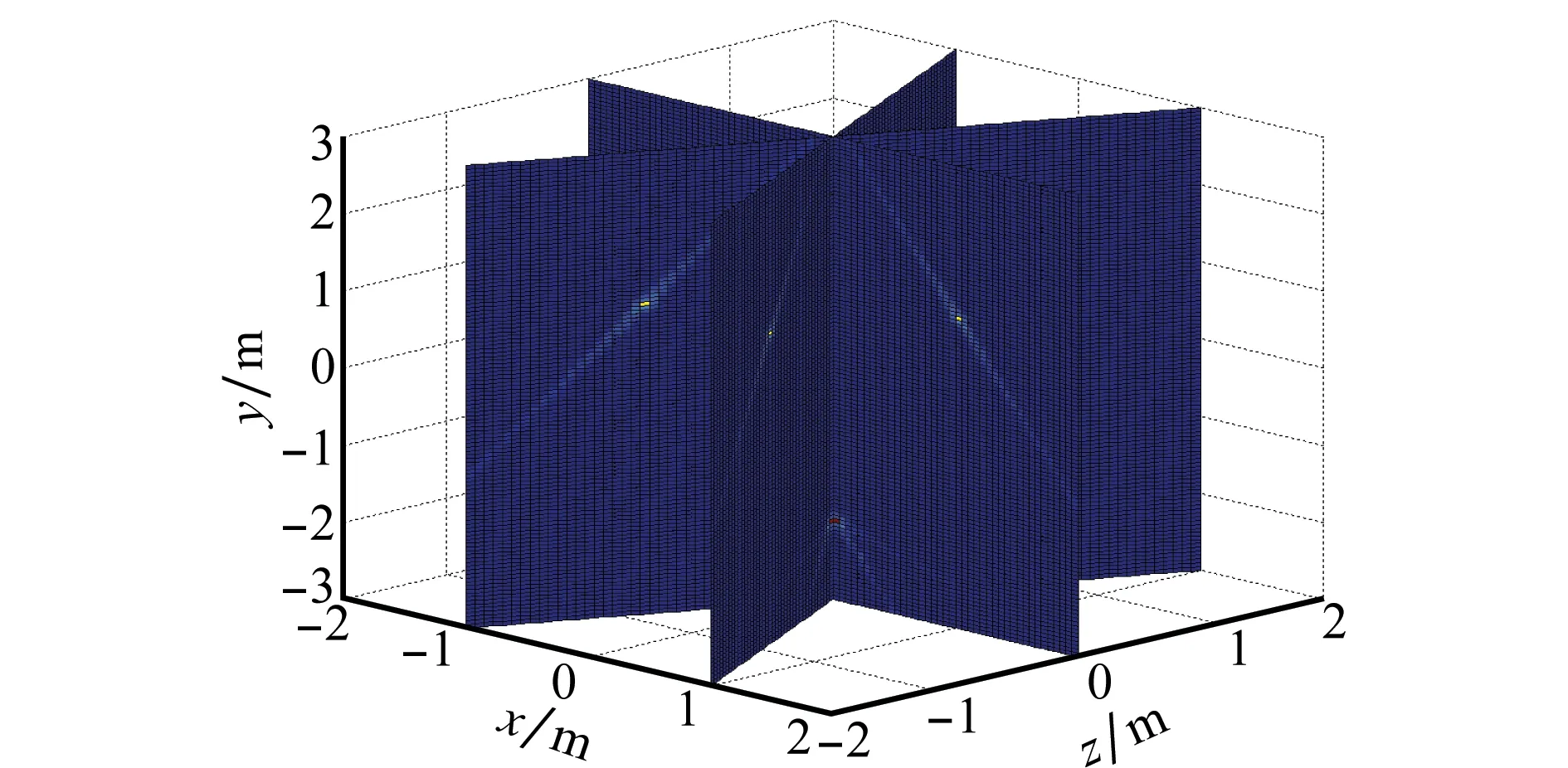
图8　锥体目标三维切面图Fig.8　Three dimensional sections of cone targets

对以上三维图像进行局部强散射点检测,锥顶散射点的坐标为[0,-2,0],其余共3个强点,坐标分别为[1,1,0],[0.5,1,-0.866],[-0.5,1,-0.866],对后3个散射点利用式(19)的方法进行三维曲线拟合。此处考虑三维切面图的特点,在参数向量A中w=[0,1,0]已知,因此三维曲线拟合可简化为二维曲线拟合;结合各散射点坐标,利用最小二乘准则求解二维曲线拟合时的最优化问题,可得需拟合的曲线形式为x2+z2=1,y=1。图9为检测到的散射点位置及目标的三维重构结果。从图9中看出重构结果与仿真目标外形结构一致,从而验证了方法的有效性。

图9　锥体目标三维重构结果Fig.9　Three dimensional reconstruction of cone targets

5　结束语

针对空间旋转对称目标三维重构问题,本文基于分布式宽带雷达组网,研究了旋转对称进动目标的三维重构方法。分析和实验证明只要夹角估计误差满足一定范围,利用文中成像方法即可得到聚焦良好的二维图像。该二维图像空间意义较为明确,因此对多幅二维图像做简单的匹配融合处理后,即可真实重构目标的三维结构。本文工作可以解决单部雷达无法获取旋转对称目标三维图像的问题,对弹道中段目标成像识别以及高速微动目标三维重构都具有一定的理论和实际意义。对于空间非旋转对称进动目标的三维重构问题,因其在结构和运动形式上与旋转对称进动目标存在较大差异,故对此尚需作进一步地研究。

[1] Chen V C, Li F, Ho S S, et al. Micro-Doppler effect in radar: phenomenon, model, and simulation study[J].IEEETrans.onAerospaceandElectronicSystems, 2006, 42, (1):2-21.

[2] Ding X F, Fan M M, Wei X Z, et al. Narrowband imaging method for spatial precession cone-shaped targets[J].ScienceinChina:TechnologicalScience, 2010,53(4):742-949.

[3] Hu J M, Zhan R H, Niu W, et al. A novel imaging method for precession targets with rotational symmetry based on back projection transform[J].JournalofElectronics&InformationTechnology,2012,34(8):1847-1852.(胡杰民,占荣辉,牛威,等.基于后向投影变换的进动旋转对称目标成像新方法[J].电子与信息学报,2012,34(8):1847-1852.)

[4] Lei T, Liu J M, Li S, et al. A novel ISAR imaging method of ballistic midcourse targets based on MP sparse decomposition[J].SystemsEngineeringandElectronics, 2011, 33(12):2649-2654.(雷腾, 刘进忙, 李松, 等. 基于MP稀疏分解的弹道中段目标微动ISAR成像新方法[J].系统工程与电子技术,2011,33(12):2649-2654.)

[5] Pan X Y, Wang W, Liu J, et al. Modulation effect and inverse synthetic aperture radar imaging of rotationally symmetric ballistic targets with precession[J].IETRadar,SonarNavigation, 2013, 7(9):950-958.

[6] Bai X R, Bao Z. High-resolution 3D imaging of precession cone-shaped targets[J].IEEETrans.onAntennasPropagation, 2014, 62(8):4209-4219.

[7] Liang B S, Zhang Q, Lou H, et al. A method of three-dimensional imaging based on micro-motion feature association for spatial asymmetrical spinning targets[J].JournalofElectronics&InformationTechnology, 2014, 36(6):1381-1388.(梁必帅, 张群, 娄昊, 等. 基于微动特征关联的空间非对称自旋目标雷达三维成像方法[J].电子与信息学报, 2014, 36(6):1381-1388.)

[8] He S S, Zhao H N, Feng C Q, et al. Imaging for complex rotation target based on singular value decomposition[J].SystemsEngineeringandElectronics,2013,35(6):1119-1205.(贺思三,赵会宁,冯存前, 等. 基于奇异值分解的复杂转动目标成像[J].系统工程与电子技术, 2013, 35(6):1119-1205.)

[9] Bai X R, Sun G C, Wu Q S, et al. Narrow-band radar imaging of spinning targets[J].ScienceinChina:InformationScience, 2011,54(4):873-883.

[10] Bai X R, Zhou F, Bao Z. High-resolution radar imaging of space targets based on HRRP series[J].IEEETrans.OnGeoscienceandRemoteSensing, 2014,52(5):2369-2381.

[11] Luo Y, Zhang Q, Yuan N, et al. Three-dimensional precession feature extraction of space targets[J].IEEETrans.onAerospaceandElectronicSystems, 2014,50(2):1313-1329.

[12] Lei T, Liu J M, Yang S C, et al. Study on feature extraction method of ballistic target based on three-station range profiles[J].JournalofAstronautics,2012,33(2):228-234.(雷腾,刘进忙,杨少春,等.基于三站一维距离像融合的弹道目标特征提取方法研究[J].宇航学报,2012,33(2):228-234.)

[13] Yao H Y, Sun W F, Ma X Y, et al. Precession feature extraction of warhead with empennages[J].ElectronicandLetters,2013, 49, (9):617-618.

[14] Subotic N S, Thelen B, Cooper K, et al. Distributed radar waveform design based on compressive sensing considerations[C]∥Proc.oftheIEEERadarConference, 2008. 1-6.

[15] Ma L, Liu J, Wang T, et al.Micro-Doppler characteristics of sliding-type scattering center on rotationally symmetric target[J].ScienceinChinaSeriesFInformationSciences, 2011,54(9):1957-1967.

[16] Yao H W, Wei X Z, Xu S K, et al. Micro-motion characteristics of non-ideal scattering centers of midcourse targets with precession[J].ActaElectronicaSinica,2012,40(9):1844-1851.(姚辉伟,魏玺章,徐少坤,等.弹道中段进动目标非理想散射中心微动特性研究[J].电子学报,2012,40(9):1844-1851.)

Three-dimensional reconstruction for spatial precession targets with rotational symmetry in radar networks

HU Xiao-wei, TONG Ning-ning, WANG Jian-ye, DING Shan-shan, ZHAO Xiao-ru

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

For the spatial precession targets with rotational symmetry,the image got in monostatic radar is only a section of targets in the line-of-sight (LOS), which cannot reflect the real 3-D structure. And the precession makes it more complex. Profited from the multi-view in radar networks, a 3-D reconstruction method for precession targets with rotational symmetry is proposed, based on radar networks. The echo model of precession targets with rotational symmetry is established firstly. On the basis of estimating the angle between LOS and the target’s symmetry axis, 2-D image of precession targets is got with complex-valued back projection, and the allowed angle error range is analyzed. Based on 2-D images from radar, a 3-D reconstruction method for targets with rotational symmetry is proposed, which realizes target’s 3-D reconstruction through 2-D images’ space calibration, matching fusion, strong scatter diction and circular curve fitting. Simulation results indicate that the method is valid.

radar networks; precession targets with rotational symmetry; complex-valued back projection; 3-D reconstruction

2015-12-22；

2016-02-04；网络优先出版日期：2016-05-03。

国家自然科学基金(61372166, 61571459)；陕西省自然科学基础研究计划项目(2014JM8308)资助课题

TN 957

10.3969/j.issn.1001-506X.2016.10.09

胡晓伟(1987-),男,博士研究生,主要研究方向为雷达目标成像与识别。

E-mail:601237134@qq.com

童宁宁(1963-),女,教授,博士,主要研究方向为雷达阵列信号处理。

E-mail:18092629021@189.com

王建业(1962-),男,教授,主要研究方向为电子科学与技术。

E-mail:17792630862@163.com