(2+1)维NNV方程的周期孤立波解和双周期孤立波解

傅海明,戴正德

(1.广州华夏职业学院 基础部,广东 广州,510935;2.云南大学 数学与统计学院,云南 昆明 650091)



(2+1)维NNV方程的周期孤立波解和双周期孤立波解

傅海明1,戴正德2

(1.广州华夏职业学院 基础部,广东 广州,510935;2.云南大学 数学与统计学院,云南 昆明 650091)

扩展了Hirota法,即将Hirota法中的测试函数用新的测试函数来替代,并利用扩展了的方法来构造(2+1)维Nizhnik-Novikov-Veselov方程的周期孤子解和双周期孤子解.显然扩展的Hirota方法也可以解其他一些非线性发展方程.

(2+1)维Nizhnik-Novikov-Veselov方程; Hirota方法;周期孤子解;双周期孤子解

随着科学技术的发展,非线性发展方程的应用越来越广泛,如非线性光学、流体力学、弹性理论和凝聚态物理等,这些领域的研究都用到非线性发展方程的解,因此,吸引了很多学者去寻求非线性发展方程的精确解.传统的求解方法主要有逆散射法[1]、Backlund法[2]、Darboux变换法[3]、Hirota双线性法[4-6]、Painlevé 展开法[7]等.近年在众多学者的努力下,又发展出许多新的求解非线性发展方程的方法,如双曲函数法[8]、齐次平衡法[9]、Jacobi椭圆函数展开法[10]、包络变换法[11-12]、ADM方法[13]、双指数函数法[14]、利用分支理论直接积分法[15]和新辅助函数法[16]等等.

Hirota法是Hirota最先使用的,用该方法可以求出非线性方程的孤子解和多孤子解.笔者把Hirota法扩展为可以求出非线性发展方程的含有周期的孤子解.然后利用扩展了的Hirota法求得(2+1)维Nizhnik-Novikov-Veselov方程

(1)

的周期孤子解和双周期孤子解.

1　方程(1)的求解过程

使用变换

(2)

再引进双线性算子

(3)

方程(1)通过式(2)和式(3)可以写成双线性型形式:

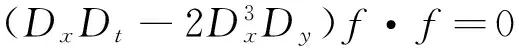
(4)

使用测试函数

f(x,y,t)=a1cosξ1+a2sinhξ2+exp(-ξ3)+a3exp(ξ3)

(5)

其中, ξi=kix+hiy+wit+ηi0(i=1,2,3),ki,hi,wi为待定常数,ηi0(i=1,2,3)为任意实常数.

把式(5)代入式(4),并且令sinξ1exp(±ξ3),cosξ1exp(±ξ3),sinhξ2exp(±ξ3),coshξ2exp(±ξ3),exp(0),sinξ1sinhξ2,cosξ1coshξ2的系数为零,得到如下代数方程组

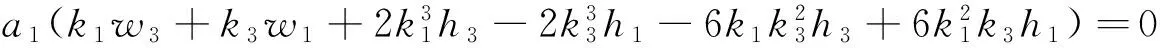
(6)

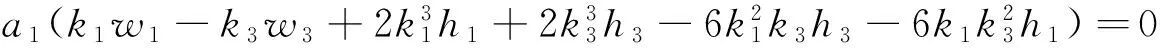
(7)

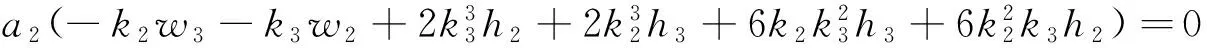
(8)

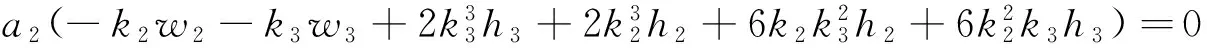
(9)

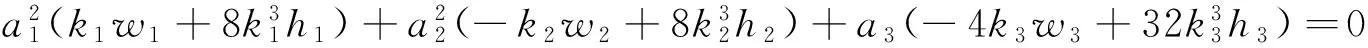
(10)

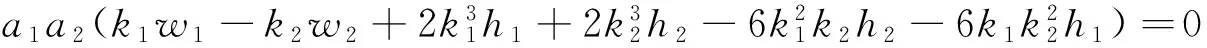
(11)

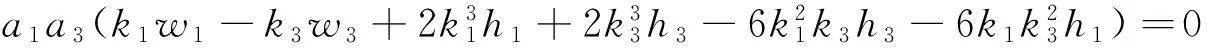
(12)

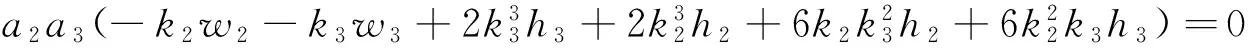
(13)

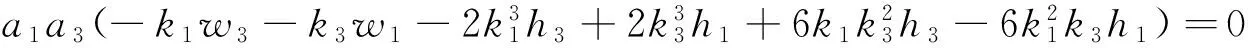
(14)

(15)

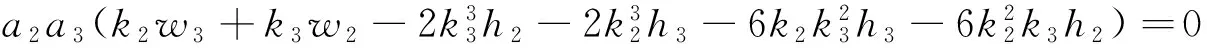
(16)

利用 MATLAB 解以上代数方程组,得到如下几种情形

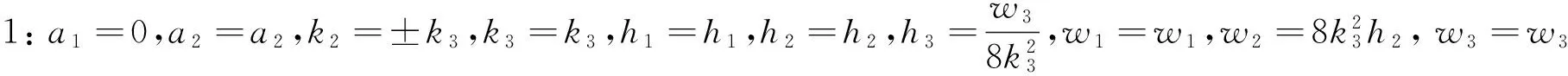
(17)

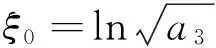
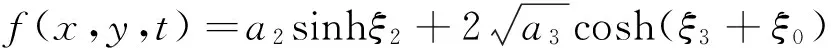
(18)

把式(18)代入式(2),得方程(1)的孤子解为

(19)

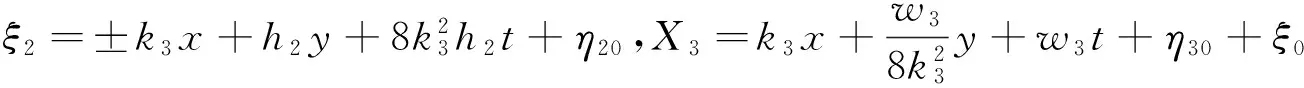
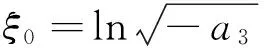
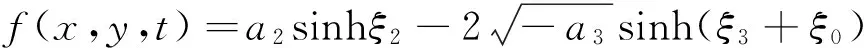
(20)

把式(20)代入式(2),得方程(1)的孤子解为

(21)

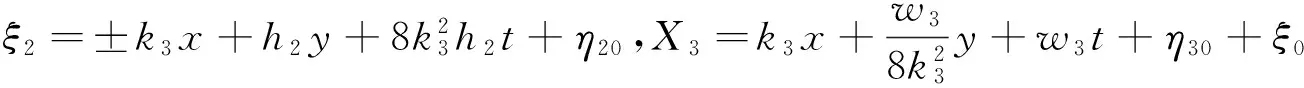
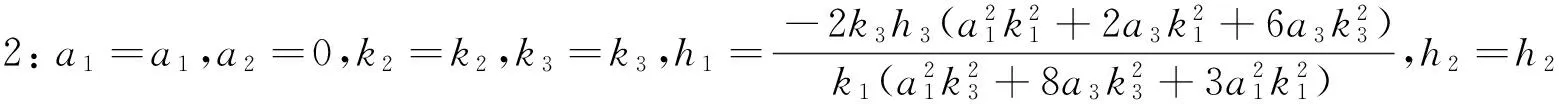
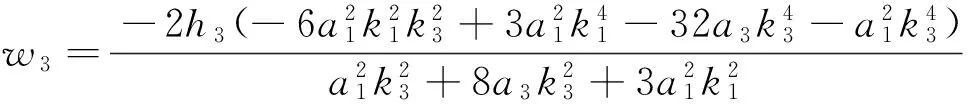
(22)

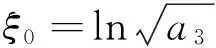
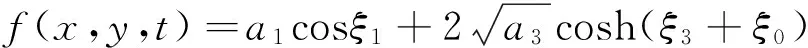
(23)

把式(23)代入式(2),得方程(1)的周期孤子解为

(24)

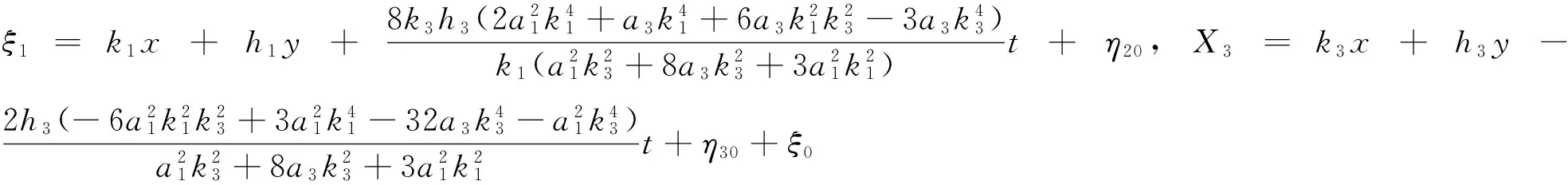
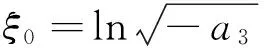
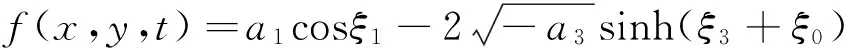
(25)

把式(25)代入式(2),得方程(1)的周期孤子解为

(26)

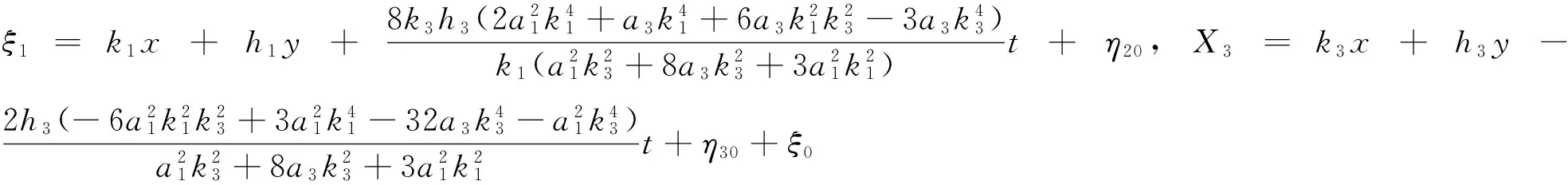
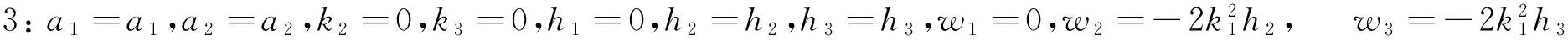
(27)

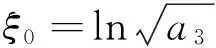
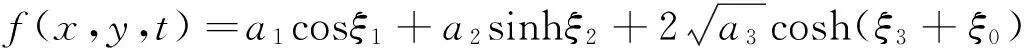
(28)

把式(28)代入式(2),得方程(1)的周期双孤子解为

(29)

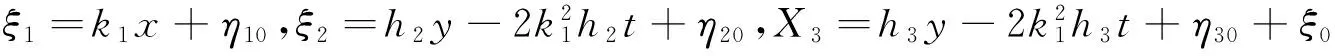
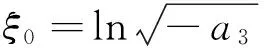
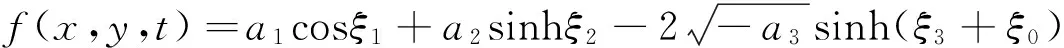
(30)

把式(30)代入式(2),得方程(1)的周期双孤子解为

(31)

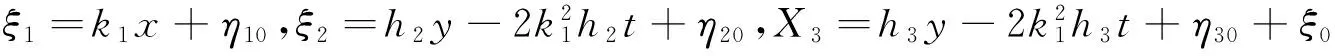
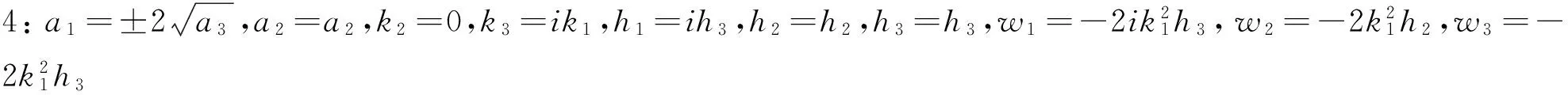
(32)

由于a3,h3任意性，不妨假设a3=1,h3=iH3,则式(32)变为

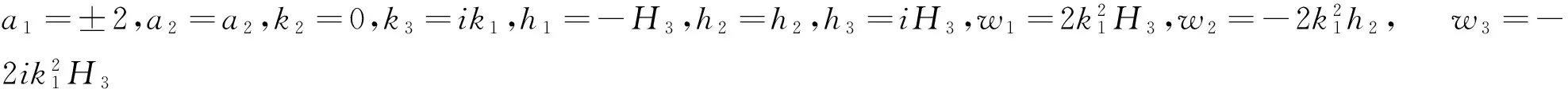
(33)

把式(33)代入式(5), 并设ξ3=iX3得

f(x,y,t)=±2cosξ1+a2sinhξ2+2cosX3,

(34)

把式(34)代入式(2),得方程(1)的双周期孤子解为

(35)

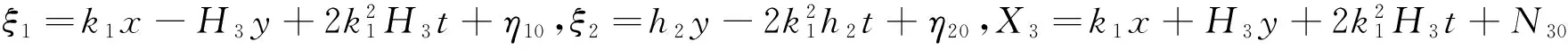
2　结论

笔者扩展了Hirota法,即将Hirota法中的测试函数用新的测试函数来替代.以(2+1)维Nizhnik-Novikov- Veselov方程为例,给出用这个扩展后的方法求周期孤子解的具体过程,这些孤子解都没曾见报道过.容易看到,这个扩展后的方法适用于相当一部分非线性方程.

[1]ABLOW ITZ M J, CLARKS ON P A. Soliton, nonlinear evolution equations and inverse scattering [M].Cambridge Univ. Press, 1991:123-136.

[2]谷超豪.孤立子理论及其应用[M ].杭州:浙江科技出版社, 1990:86-98.

[3]MAT VEEV V B, S ALLEM A.Daroux transformations and solitons[M]. Berlin: Springer, 1991:326-387.

[4]HIROTAR. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons[J]. Phys Rev lett, 1971, 27: 1192-1194.

[5]傅海明,戴正德.(3+1)维K-P方程的周期孤波解[J].山西大学学报(自然科学版),2010, 33(1): 4-7.

[6]傅海明,戴正德.(3+1)维孤子方程的周期孤波解[J].东北师范大学学报(自然科学版),2011, 47(2): 32-34,42.

[7]楼森岳.推广的 Painlevé 展开及 KdV方程的非标准截断解[J].物理学报,1998,47: 1739-1745 .

[8]李志斌,张善卿.非线性波方程准确孤立波解的符号计算[J].数学物理学报,1997,17(1):81-89.

[9]WANG M L, ZHOU YB, LI ZB. Application of homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J]. Phys Lett A, 1996,213:67-75.

[10]刘式适,傅遵涛,刘式达，等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报, 2001,50 (11):2068-2073 .

[11]FU Hai-Ming, DAI ZHeng-De. Exact chirped solitary-wave solutions for Ginzburg-Landau equation[J]. Communications in Nonlinear Science and Numerical Simulations，2010(15):1462- 1465.

[12]傅海明,戴正德.一类非线性偏微分方程的新孤立波解[J].西北师范大学学报:自然科学版,2014,50 (2):47-49.

[13]SALAN M, KAYA D. An application of the ADM to seven-order Sawada-Kotara equations[J]. Applied Mathematics and Computation, 2004,157: 93-101.

[14]FU Hai-Ming, DAI ZHeng-De. Double Exp-function Method and Application[J]. International Journal of Nonlinear Science and Numerical Simulation，2009,10(7):927-933.

[15]LI Ji-Bin, ZHANG Li-Jun. Bifurcations of traveling wave solution in generalized Pochhammer-Chree equation[J]. Chaos, Soitons and Fractals, 2002,14:581-593.

[16]傅海明,戴正德.新辅助函数法及(2+1)维Burgers方程的精确解[J].江苏师范大学学报(自然科学版),2015,33(4):25-29.

Periodic-soliton wave solutions and double periodic-soliton wave solutions for (2+1)-dimensional NNV equation

FU Haiming1, DAI Zhengde2

(1. Department of Basic Courses, Guangzhou Huaxia Technical College, Guangzhou 510935, China;2.College of Mathematics & Statistics, Yunnan University, Kunming 650091, China)

Hirota method proposed recently is extended to construct more exact solutions of nonlinear evolution equations. To be more precise, new text function is used instead of text function in Hirota method. By using the extended Hirota method, (2+1)-dimensional Nizhnik-Novikov-Veselov equation is solved an abundance of exact periodic soliton wave solutions and double periodic soliton wave solutions. Obviously, the extended Hirota method can be applied to solve some other nonlinear evolution equations as well.

(2+1)-dimensional Nizhnik-Novikov-Veselov equation; Hirota method; periodic-soliton wave solutions; double periodic-soliton wave solutions

2016-04-04;

2016-05-16

国家自然科学基金资助项目(No.11061028)

傅海明(1981- ),男,广东从化人,讲师,硕士,主要从事可积系统与孤立子方面的研究.

O175.29

A

1671-9476(2016)05-0039-05

10.13450/j.cnki.jzknu.2016.05.010