大学生学习投入与学业表现的相关性分析

张爱武,李万斌

(江苏盐城师范学院 数学与统计学院，江苏 盐城 224002)



大学生学习投入与学业表现的相关性分析

张爱武,李万斌

(江苏盐城师范学院 数学与统计学院，江苏 盐城 224002)

研究了当代大学生学习投入与学业表现之间的相关关系．综合利用多元线性回归和主成分分析等现代统计方法，深入讨论了学业表现与其他诸如行为投入、认知投入和情感投入等影响因素之间的关系．文后通过实证分析说明了行为投入、认知投入、情绪投入均与学业表现之间呈现正向相关关系.

学习投入；多元线性回归分析；主成分分析

现代高等教育质量观主要侧重学生投入于各种有效学习活动的程度，以及关注学生的发展质量[1]．学习投入指这样一种状态：一个人在学习时精力充沛且心理韧性较好，他能够认识到学习的重要性，对学习有较强的积极性.其中，学习投入主要包括三个方面：行为投入、认知投入和情绪投入.

学习投入是国内以及国外教育界和学术界关注的热点问题．虽然朱红、史静寰、Brophy J、McIntyre D J、Natriello G等国内外学者从不同角度构建了学习投入的评价模型，但是很少有学者研究学习投入与学业表现之间的密切关系[2-6]．学习投入是影响学业表现的重要因素，如果学生对学习的投入较低，就会导致较低的学业表现．反之，如果学生对学习的投入较高，一般也会导致较高的学业表现.因此，为了探讨江苏省大学生的学习投入与学业表现之间是否存在着一定的相关关系以及它们之间存在着怎样的相关关系，笔者通过多元回归分析和主成分回归分析的方法[7-9]对学生学习投入和学业成绩的实际数据进行实证分析，归纳学习投入和学业成绩间的相关关系．

首先，笔者选取学习投入的三个方面，即行为投入、认知投入、情绪投入作为三个变量，把学生的最近一次期末学业综合成绩作为学业表现，对它们进行多元回归分析，对得到的回归结果进行综合评价.其次，对三个变量进行主成分分析，以找到一个综合指标因子作为学习投入，再把学习投入与学业表现进行主成分回归分析.最后，归纳总结出学习投入与学业表现两者之间的相关关系.

1　初步分析

1.1数据获取和评价指标体系建立

为了得到相关的数据，研究小组在某高校进行了问卷调查.调查问卷设计了20道关于学习投入三个方面的问题，通过这一系列问题来了解大学生在学习投入三个方面中的表现.此次调查采用了随机抽样的方法，对不同年级、不同专业的大学生进行抽样调查，当面发放调查问卷，并现场回收调查问卷.共发放310份调查问卷，收回266份问卷.

在研究学习投入与学业表现之间的相关关系时，选取一些与学习投入可能相关的变量，用X1表示行为投入，X2表示认知投入，X3表示情绪投入，Y表示学业表现.

1.2变量的相关分析

本节分别对行为投入、认知投入、情绪投入与学业表现进行相关分析.图1给出了Y与X1、X2、X3的散点图，且在表1中给出Y与X1、X2、X3的相关系数.

从图1中，可以发现行为投入、认知投入、情绪投入与学业表现有一定的相关性.此外，样本点主要围绕一条向右上方倾斜的拟合线附近上下波动，呈现出Y与X1、X2、X3的正相关性.

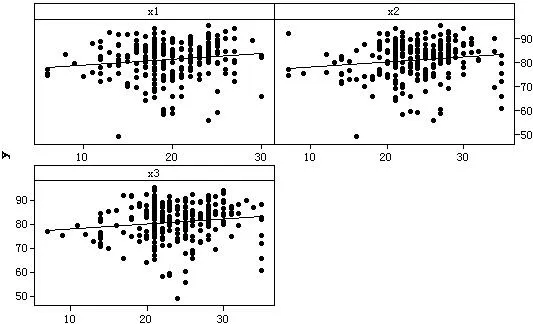
图1　Y与X1、X2、X3的散点图表1　相关系数

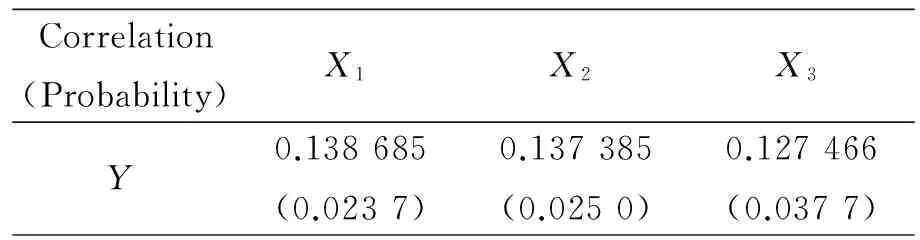
Correlation(Probability)X1X2X3Y0.138685(0.0237)0.137385(0.0250)0.127466(0.0377)

表1给出了Y与X1、X2、X3的相关系数r及其p值，相关系数均为正数，说明行为投入、认知投入、情绪投入与学业表现呈正相关.

2　模型构建

为了进一步研究X1、X2、X3与Y之间的关系，本文对Y与X1、X2、X3进行多元线性回归分析和主成分回归分析，试用具体的模型来描述它们之间的关系.

2.1 建立多元回归模型

Eviews统计软件的估计结果如图2所示：

图2　多元线性回归结果

从图2中可以看出，在显著性水平α=0.05的情况下，变量X1、X2、X3的p值均显著大于α值，则X1、X2、X3对Y的影响均不显著.R2的值接近为零，说明变量X1、X2、X3对Y的解释较小.而F统计量的p值为0.116 652大于α值，则表明拟合模型不显著.

表2　相关系数矩阵

表2给出了X1、X2、X3之间的相关系数，从此可以发现X1、X2的相关系数达到0.77以上，因此这两个变量高度相关.而X1、X3和X2、X3之间的相关系数分别为0.720 3,0.693 4.从相关系数矩阵可以得出，X1、X2、X3之间存在着高度的相关性，这影响着模型的显著性.为了解决变量之间的相互影响，本文对变量进行主成分分析，然后进行主成分回归，试图拟合出较为合适的模型.

2.2主成分分析

运用Eviews统计分析软件可以输出以下结果：

表3　相关矩阵特征值

表3给出了相关矩阵特征值、差异值、贡献率、累计贡献率.特征值越大，它所对应的主成分变量包含的信息就越多.此处输出结果中前两个主成分特征值的累计贡献率为92.44%，说明前两个主成分几乎包含了原来3个指标的信息.主成分的实际意义由各线性组合中权数较大的几个指标的综合意义来确定.因此只需用前两个主成分就能很好地概括这组数据.

表4　特征向量

由表4相关数据给出了特征根对应的特征向量，第一个特征根对应的特征向量为：

u1=(0.579 556,0.586 402,0.565 904),

第二个特征根对应的特征向量为：

u2=(-0.519 714,-0.268 920,0.810 913),

则第一主成分得分为：

Z1=0.579 556X1+0.586 402X2+

0.565 904X3,第二主成分得分为：

Z2=-0.510 714X1-0.268 920X2+

0.810 913X3.

所以，综合前两个主成分对学业表现的影响，定义如下的主成分得分值为：

Z=0.818 8Z1+0.105 6Z2，即Z为学习投入.下面，试用主成分回归分析方法求出学习投入与学业表现之间的定量关系式.

2.3建立主成分回归模型

运用Eviews统计分析软件可以输出以下结果：

图3　学业表现与学习投入因子的散点图

从图3中所描绘的学业表现(Y)与学习投入(Z)的散点图来看，在Z∈(24,40)的范围内Y与Z之间存在正向相关关系,即学习投入的数值越大，学业表现的数值也就越大.反之，则学习投入的数值越小，学业表现得数值也就越小.此外，在散点图中，Eviews软件拟合出一条回归直线，样本点主要围绕回归直线上下波动，这条回归直线也说明Y与Z呈正相关，即大学生的学业表现和学习投入之间是正相关的关系.

运用Eviews分析软件进行回归分析，采用最小二乘估计方法，得到主成分回归的拟合模型为Y=74.936 25+0.186 563Z，其中Y为学业表现，Z为学习投入.

在显著性水平α=0.05的情况下，Z的p值为0.015 7，小于α值，则拒绝原假设，即说明Z对Y的影响是显著的.从上面的拟合模型中，可以得出学习投入与学业表现之间呈正相关.虽然可决系数和调整后的可决系数均不高，但是F检验的p值小于α值，则模型通过F检验，即主成分回归拟合的模型是显著的.

3　结论及建议

3.1 结论

通过借鉴已有的研究成果和学习投入和学业表现的主要内涵，对学习投入和学业表现进行建模，初步探讨二者之间的相关关系.从以上分析可以得出：行为投入、认知投入、情绪投入均与学业表现之间呈现一定的正向相关关系.此外，从上面的初步分析中可以看出，行为投入对学业表现的影响最为显著，其次是认知投入和情绪投入.由于三个变量之间存在多重共线性，本文后半部分进行了主成分回归建模.通过主成分分析构建一个学习投入因子，进而得到学习投入与学业表现的回归方程，定量地描述了二者的正向相关性，可以为高校学生的成绩评估提供一些参考.

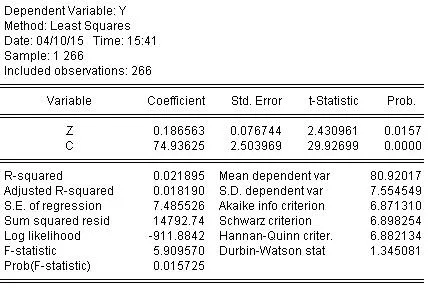
图4　主成分回归结果

当然，本文尚存在一些局限性，有待做进一步的研究.归纳起来，主要有以下两点：第一，本文只是从学习投入的其中三个维度与学业表现进行了建模，分析的变量较少；第二，由于数据来源于简单地问卷调查，存在很大的误差，导致模型拟合效果不理想.因此，学习投入与学业表现的相关性的评价模型有待于进一步研究.

3.2 建议

通过前面对行为投入、认知投入、情绪投入与学业表现的初步分析，有以下几点值得在今后的教育改革中加以注意.

第一，重视对影响学生学业表现的关键因素进行分析，通过适当干预来改善学生学习效果. 本文选取了行为投入、认知投入、情绪投入这三个变量.在某高校大学生调查问卷得到的数据的支持下，肯定了三个变量对大学生的学业表现具有正向影响，其中行为投入最为重要.教育部门和高校可以通过积极引导学生自主学习和提高他们的学习乐趣来进一步提高教育质量.

第二，在坚持基础教育均衡发展的前提下，加强学生对学习重要性的认识.平时，教师可以适时地找同学谈心，多了解一下学生的心理，对他们进行一些贴心地说教，鼓励学生好好学习，学会因材施教，实行针对性教育等.

第三，把握学习投入与学业表现之间的正相关关系，探究一些提高大学生的学习投入的方法和策略，从而有效地提高学生的学业成绩.

大数据时代的到来，对教育事业发展和教育科研提出了更大的挑战，也提供了更多的机会.面对海量数据，如何通过适当的手段展开分析去获取对教育改革与发展有效的信息，成为每一个教育工作者义不容辞的责任[10].对教育界而言，大学生的学习投入与学业表现之间的相关关系需要用更科学、更合理的方法来进一步研究.本文的分析，只是初步地为教育界提供一些建议，具有一定的研究价值和现实意义，但是还需要深入探讨，不断地完善，为提高大学的教育质量提供一定的帮助.

[1]朱红灿. 大学生学习投入影响因素的研究—基于学习行为投入、情绪投入、认知投入维度[J].高教论坛，2014，29(4)：36-40.

[2]朱红. 高校学生参与度及其成长的影响机制—十年首都大学生发展数据分析[J]. 清华大学教育研究，2010，31(6)：35-43.

[3]史静寰，文雯. 清华大学本科教育学情调查报告2010[J]. 清华大学教育研究，2012，33(1)：4-16.

[4]Brophy J. Conceptualizing StudentMotivation[J]. Educational psychologist，1983， 18(5)：200-215.

[5]McIntyre D J，Copenhaver R W，Byrd D M，et al. A Study of Engaged Student Behaviour within Classroom Activities During Mathematics Class[J]. Journal of Educational Research，1983, 77(2)：55-59.

[6]Natriello G. Problems in the Evaluation of Students and Student Disengagement from Secondary Schools[J]. Journal of research and Development in Education，1984，17(4)：4-24.

[7]王芳，陈胜可，冯国生. SAS统计分析与应用[M]. 北京：电子工业出版社，2011：160-163.

[8]汤银才. R语言与统计分析[M]. 北京：高等教育出版社，2008：278-279.

[9]陶锦莉，郑洁. 长三角地区人才竞争力的比较研究[J]. 南京社会科学，2007，17(9)：21-25.

[10]唐一鹏. 从上海PISA2012透视学生能力分位的影响因素[J]. 上海教育科研，2014，16(6)：15-19.

Correlation analysis between college students’learning engagement and academic performance

ZHANG Aiwu,LI Wanbin

( (School of Mathematics, Yancheng Teachers University, Jiangsu 224002,China)

This paper considers the correlation between the learning engagement and academic performance. By combining the multivariate linear regression with principal component method, the dependence of academic performance on other affecting factors, such as behaviour engagement, cognitive engagement and affective engagement, is intensively analyzed. The empirical study also demonstrates the positive relationship between the academic performance and other affecting variables in the end of this paper.

learning engagement; multivariate linear regression analysis; principal component analysis

2016-03-07;

2016-04-08

江苏省教育科学十二五规划课题(No.D/2013/01/129)资助

张爱武(1963- )，男，江苏盐城人，教授，主要研究：统计分析与诊断、高等教育研究，E-mail:zaw_017@163.com，电话：15951558680

G645

A

1671-9476(2016)05-0007-04

10.13450/j.cnki.jzknu.2016.05.002