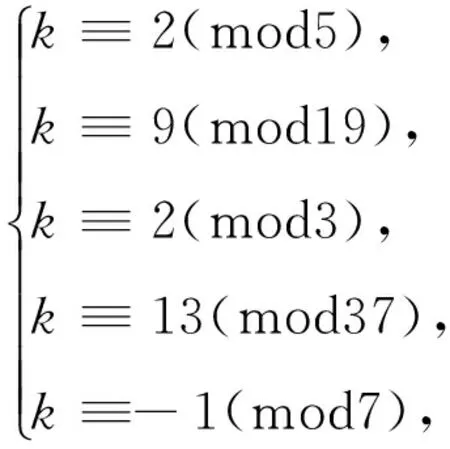关于覆盖同余式的一个应用
2016-10-17管训贵
管训贵
(泰州学院 数理学院,江苏 泰州 225300)
关于覆盖同余式的一个应用
管训贵
(泰州学院 数理学院,江苏 泰州 225300)
建立了一组覆盖同余式并通过对非负整数n进行分类等方法,给出了使2kpn+1对每一个非负整数n均为合数的k值,这里素数p=7,13及p≡5(mod6).
覆盖同余式;合数;剩余;模
覆盖同余式的构造问题是数论中较为复杂的问题之一,目前这方面已有许多非常重要的成果[1-6].
由于覆盖同余式通过一切非负整数,故可用来解决一类与合数有关的数论问题.1980年国际数论会议上,著名数学家P.Erdös 曾提出“能否找到一个正整数k,使得k·2n+1对每一个非负整数n均为合数?”的求解问题.文献[7]利用覆盖同余式证明了k的存在性,并给出了21类这样的k值.作为该问题的延续,本文利用一组覆盖同余式证明了以下一般性的结果.
定理设素数p=7,13及p≡5(mod6),则存在正整数k,使得2kpn+1对每一个非负整数n均为合数.
1 预备知识和引理
定义若每一个非负整数n都至少满足下列同余式中的一个:
n≡a1(modn1),n≡a2(modn2),…,n≡as(modns),
(1)
这里1 引理1 n≡0(mod2),n≡0(mod3),n≡1(mod4),n≡5(mod6),n≡7(mod12)是一组覆盖同余式. 证全体非负偶数满足n≡0(mod2);全体正奇数可按模12分成六类: 12r+1,12r+3,12r+5,12r+7,12r+9,12r+11,r=0,1,…. 这里12r+3,12r+9满足n≡0(mod3),12r+1,12r+5满足n≡1(mod4),12r+11,12r+7分别满足n≡5(mod6)和n≡7(mod12). 引理2[8]设奇数n>1,则方程x2+x+1=yn仅有正整数解(x,y,n)=(18,7,3). 引理6设素数p>13且p≡5(mod6),则存在素数q>13,使q∣(p3-1). 证只需证在题设条件下,存在素数q>13,使q∣(p2+p+1),或 p2+p+1≡0(modq). (2) 即可. p2+p+1=7a·13b, (3) 这里a,b是不全为0的非负整数. 当a=0或b=0或a,b同为偶数时,结合引理2知,式(3)不成立.下设a,b为正整数且a,b中至少有一个为奇数. 若a=b=1,则由式(3)得p2+p+1=91,解得p=9,不合题意.因此a,b中至少有一个是大于1的奇数.由式(3)得 (4) s2-91r2=-3. (5) 根据引理3~5,方程(5)的全部正整数解(s,r)=(sn,rn)由以下两个非结合类给出: (6) 或 (7) 由式(6)得 sn+2=3 148sn+1-sn,s0=19,s1=59 936. (8) 因sn为奇数,故n必为偶数.对式(8)模3得剩余序列周期为2,且当n为偶数时,有sn≡1(mod3),即2p+1≡1(mod3),推知p=3与p>13矛盾.故式(6)不成立. 由式(7)得 sn+2=3 148sn+1-sn,s0=-19,s1=124. (9) 对式(8)模5得剩余序列周期为2,且当n为偶数时,有sn≡1(mod5),即2p+1≡1(mod5),推知p=5与p>13矛盾.故式(7)不成立.于是式(4)不成立. 由式(3)得 (10) s2-13r2=-3. (11) 根据引理3~5,方程(11)的全部正整数解(s,r)=(sn,rn)由以下两个非结合类给出: (12) 或 (13) 由式(12)得 sn+2=1 298sn+1-sn,s0=7,s1=9 223. (14) 由式(14)知,对任意非负整数n,有sn≡1(mod3),即2p+1≡1(mod3),推知p=3与p>13矛盾.故式(12)不成立. 由式(13)得 sn+2=1 298sn+1-sn,s0=-7,s1=137. (15) 由式(15)知,对任意非负整数n,有sn≡1(mod8),即2p+1≡1(mod8),推知p≡0(mod4),不可能.故式(13)不成立.于是式(10)不成立. 若a=1,则由式(3)得 (16) s2-28r2=-3. (17) 根据引理3~5,方程(17)的全部正整数解(s,r)=(sn,rn)由以下两个非结合类给出: (18) 或 (19) 由式(18)得 rn+2=254rn+1-rn,r0=1,r1=247. (20) 考虑到13∣rn,对式(20)模13得剩余序列周期为7,且有n≡1(mod7). 由式(19)得 sn+2=254sn+1-sn,s0=-5,s1=37. 易知,对任意非负整数n,有sn≡1(mod6),即2p+1≡1(mod6),推知p=3与p>13矛盾.于是式(16)不成立. 若a≥3,则由式(3)得 (21) s2-7r2=-3. (22) 根据引理3~5,方程(22)的全部正整数解(s,r)=(sn,rn)由以下两个非结合类给出: (23) 或 (24) 由式(23)得 sn+2=16sn+1-sn,s0=2,s1=37. (25) 因sn为奇数,故n必为奇数.对式(25)模3得剩余序列周期为2,且当n为奇数时,有sn≡1(mod3),即2p+1≡1(mod3),推知p=3与p>13矛盾.故式(23)不成立. 由式(24)得 rn+2=16rn+1-rn,r0=1,r1=2. (26) 对式(26)模7得剩余序列周期为7,且当n≡6(mod7)时,7∣rn;对式(26)模13得剩余序列周期为14,且当n≡3,10(mod14)即n≡3(mod7)时,13∣rn.此时有6≡3(mod7),显然不可能.故式(24)不成立.于是式(21)不成立.引理6得证. 分两步进行: Ⅰ.若p=5,由于52≡1(mod3),53≡1(mod31),54≡1(mod13),56≡1(mod7),512≡1(mod601),所以 当n≡0(mod2),即n=2m时,有2k·5n+1=2k·52m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·5n+1=2k·53m+1≡2k+1(mod31); 当n≡1(mod4),即n=4m+1时,有2k·5n+1=2k·54m+1+1≡-3k+1(mod13); 当n≡5(mod6),即n=6m+5时,有2k·5n+1=2k·56m+5+1≡-k+1(mod7); 当n≡7(mod12),即n=12m+7时,有2k·5n+1=2k·512m+7+1≡-10k+1(mod601). 因此,只需k满足下列同余方程组 (27) 则由引理1知,对每一个非负整数n,2k·5n+1至少被3,31,13,7,601中一数整除,因而2k·5n+1必是一个合数.由计算知,式(27)等价于下列同余方程组 进而等价于 (28) 由于模m1=21,m2=13,m3=31,m4=601两两互素,故式(28)可用孙子剩余定理求得k≡1 107 583(mod5 086 263).于是所求的正整数k=1 107 583+5 086 263t,这里t是任意非负整数. 若p=7,由于72≡1(mod3),73≡1(mod19),74≡1(mod5),76≡1(mod43),712≡1(mod13),所以 当n≡0(mod2),即n=2m时,有2k·7n+1=2k·72m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·7n+1=2k·73m+1≡2k+1(mod19); 当n≡1(mod4),即n=4m+1时,有2k·7n+1=2k·74m+1+1≡-k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·7n+1=2k·76m+5+1≡-12k+1(mod43); 当n≡7(mod12),即n=12m+7时,有2k·7n+1=2k·712m+7+1≡-k+1(mod13). 因此,只需k满足下列同余方程组 (29) 则由引理1知,对每一个非负整数n,2k·7n+1至少被3,19,5,43,13中一数整除,因而2k·7n+1必是一个合数.由计算知,式(29)等价于下列同余方程组 进而等价于 (30) 由于模m1=195,m2=19,m3=43两两互素,故式(30)可用孙子剩余定理求得k≡58 111(mod159 315).于是所求的正整数k=58 111+159 315t,这里t是任意非负整数. 若p=11,由于112≡1(mod5),113≡1(mod19),114≡1(mod3),116≡1(mod37),1112≡1(mod7),所以 当n≡0(mod2),即n=2m时,有2k·11n+1=2k·112m+1≡2k+1(mod5); 当n≡0(mod3),即n=3m时,有2k·11n+1=2k·113m+1≡2k+1(mod19); 当n≡1(mod4),即n=4m+1时,有2k·11n+1=2k·114m+1+1≡k+1(mod3); 当n≡5(mod6),即n=6m+5时,有2k·11n+1=2k·116m+5+1≡17k+1(mod37); 当n≡7(mod12),即n=12m+7时,有2k·11n+1=2k·1112m+7+1≡k+1(mod7). 因此,只需k满足下列同余方程组 (31) 则由引理1知,对每一个非负整数n,2k·11n+1至少被5,19,3,37,7中一数整除,因而2k·11n+1必是一个合数.由计算知,式(31)等价于下列同余方程组 进而等价于 (32) 由于模m1=15,m2=19,m3=37,m4=7两两互素,故式(32)可用孙子剩余定理求得k≡50 777(mod73 815).于是所求的正整数k=50 777+73 815t,这里t是任意非负整数. 若p=13,由于132≡1(mod7),133≡1(mod61),134≡1(mod17),136≡1(mod3),1312≡1(mod5),所以 当n≡0(mod2),即n=2m时,有2k·13n+1=2k·132m+1≡2k+1(mod7); 当n≡0(mod3),即n=3m时,有2k·13n+1=2k·133m+1≡2k+1(mod61); 当n≡1(mod4),即n=4m+1时,有2k·13n+1=2k·134m+1+1≡9k+1(mod17); 当n≡5(mod6),即n=6m+5时,有2k·13n+1=2k·136m+5+1≡2k+1(mod3); 当n≡7(mod12),即n=12m+7时,有2k·13n+1=2k·1312m+7+1≡-k+1(mod5). 因此,只需k满足下列同余方程组 (33) 则由引理1知,对每一个非负整数n,2k·13n+1至少被7,61,17,3,5中一数整除,因而2k·13n+1必是一个合数.由计算知,式(33)等价于下列同余方程组 进而等价于 (34) 由于模m1=7,m2=61,m3=17,m4=15两两互素,故式(34)可用孙子剩余定理求得k≡59 566(mod108 885).于是所求的正整数k=59 566+108 885t,这里t是任意非负整数. Ⅱ.设素数p>13.易验证:p2+p+1≡0(mod32),p2+p+1≡0(mod5),p2+p+1≡0(mod11).根据引理6,p>13时,必存在素数q>13,使得q∣(p3-1),即p3≡1(modq). 又若p≠3,5,7,13,则gcd(p,3·5·7·13)=1,进而p2≡1(mod3),p4≡1(mod5), p6≡1(mod7),p12≡1(mod13),所以 当n≡0(mod2),即n=2m时,有2kpn+1=2kp2m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2kpn+1=2kp3m+1≡2k+1(modq); 当n≡1(mod4),即n=4m+1时,有2kpn+1=2kp4m+1+1≡2pk+1(mod5); 当n≡5(mod6),即n=6m+5时,有2kpn+1=2kp6m+5+1≡2p5k+1(mod7); 当n≡7(mod12),即n=12m+7时,有2kpn+1=2kp12m+7+1≡2p7k+1(mod13) 因此,只需k满足下列同余方程组 (35) 则由引理1知,对每一个非负整数n,2kpn+1至少被3,q(q为大于13的素数),5,7,13中一数整除,因而2kpn+1必是一个合数.不难知道,式(35)中第三、四、五个同余方程分别有唯一解k≡a(mod5),k≡b(mod7),k≡c(mod13),故式(35)等价于下列同余方程组 由孙子剩余定理可得k. 综上所述,对任意素数p≡5(mod6)及p=7,13,存在正整数k,使得2kpn+1对每一个非负整数n均为合数.定理得证. p2+p+1=3·7a·13b, (36) 这里a,b是不全为0的非负整数. 只需证(36)式不成立,则当p≡1(mod6)时,便存在素数q>13,使q∣(p3-1).因此,有下列 猜想:若素数p≡1(mod6),则存在正整数k,使得2kpn+1对每一个非负整数n均为合数. [1]Schinzel A.Reducibility of polynomials and covering systems of congruences[J]. Acta Arith.,1967/1968(13):91-101. [2] 孙琦,万大庆,旷京华.关于覆盖同余式组的一个注记[J].数学研究与评论,1984,4(2):1-3. [3] 孙智伟,孙智宏. 关于覆盖同余式组的若干结果[J].西南师范大学学报,1987(1):10-15. [4]孙智伟.关于不同模覆盖系[J].扬州师院学报(自然科学版),1991,11(3):21-27. [5] SunZ.W.On exactly m times covers[J]. Israel J.Math.,1992,77:345-348. [6]及万会. 关于覆盖同余式组[J].贵州师范大学学报(自然科学版),2000,18(4):72-75. [7]侯炮明,王炳安. 一类覆盖同余式组的一个应用[J].辽宁工程技术大学学报(自然科学版),1999,18(1):93-97. [8] Nagell T. Note sur I’é quation indé terminé (xe-1)/(x-1)=yq[J]. Norsk. Mat.Tidsskr,1920,2:75-78. [9]柯召,孙琦.谈谈不定方程[M].上海:上海教育出版社,1980. An application on covering systems of congruences GUAN Xungui (School of Mathematics and Physics ,Taizhou University,Taizhou Jiangsu 225300, China) In this paper, a kind of covering congruence group is constructed and with a method of classification for nonnegative integern,we give a method ofkvalue computation to make 2kpn+1 the composite for every nonnegative integern,wherepbe prime withp=7,13 and p≡5(mod6). covering systems of congruences;composite number;residue;moduli 2016-01-12; 2016-03-16 江苏省教育科学“十二五”规划课题(No.D201301083);泰州学院教授基金项目(No.TZXY2015JBJJ002);云南省教育厅科研课题(No.2014Y462) 管训贵(1963- ),男,江苏兴化人,教授,研究方向:数论. E-mail:tzszgxg@126.com O156.1 A 1671-9476(2016)05-0001-06 10.13450/j.cnki.jzknu.2016.05.001



















2 定理的证明