原子力显微镜探针悬臂弹性常数校正技术进展

屈泽华，卜　娟，潘晓霞

（聚合物分子工程国家重点实验室，复旦大学高分子科学系，上海 200433）

原子力显微镜探针悬臂弹性常数校正技术进展

屈泽华，卜娟，潘晓霞

（聚合物分子工程国家重点实验室，复旦大学高分子科学系，上海 200433）

利用原子力显微镜对材料表面的力学性能进行定量表征时，需要准确知道原子力显微镜探针悬臂的弹性常数，所以对弹性常数进行校正十分重要。该文综述近年来对探针悬臂弹性常数的校正方法，主要包括维度法、静态挠度法、动态挠度法。维度法对不同悬臂形状（主要针对矩形、V型）进行阐述，分析不同方法使用的数学模型与优缺点；静态挠度法不仅对方法的数学模型进行阐述，还着重介绍近年来对该方法精确度的改进研究；动态挠度法以附加质量法、Sader法与热调谐法分别阐述，比较3种方法的模型特点与先进性；最后分析常用探针适合使用的校正方法，对今后校正方法的发展提供参考。

探针悬臂；弹性常数；校正；综述

0　引　言

原子力显微镜发展到今天，人们已经不再局限于仅用其实现对材料表面的显微成像，而是更多地关注其对物化性能的检测，对力学性能的表征便是其一[1-2]。原子力显微镜在进行力学表征时是通过测定探针与样品表面的相互作用的力曲线实现的。在测定力-位移曲线时，检测的探针与样品之间的作用力即微悬臂的弹力，它遵循Hooke定律：F=-Kδc（K为微悬臂的弹性常数，δc为微悬臂的偏移量）。要想获得准确的探针与样品之间的作用力，必须知道悬臂的弹性常数，悬臂的弹性常数不仅影响原子力显微镜测定力的大小，还影响探针的扫描速度以及扫描图像的质量，通常市售探针盒上会标注一个供参考的弹性常数，但是由于悬臂梁的制作工艺造成每根探针的弹性常数都不同，都与标注值有偏差，所以，在定量表征力学性能前必须先对弹性常数进行校正[3]。本文将针对近年来探针悬臂弹性常数校正方法的研究进展作详细综述。一般来讲，校正探针悬臂弹性常数的方法可归结为维度法、静挠度测量法和动挠度测量法3种方法。

1　维度法

通常原子力探针悬臂的形状主要分为两种：矩形和V型。维度法对于矩形探针模型比较容易建立，弹性常数可以通过加载在悬臂自由端时沿着光束的力来计算。通过假定一个小的垂直的反射量Z，用下式[4]计算：

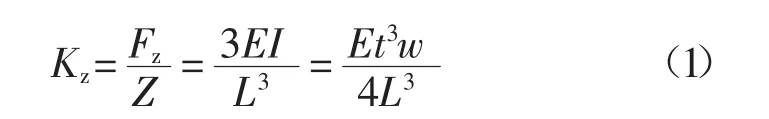
式中：L、w、t——悬臂的长度、宽度和厚度；

E——杨氏模量；

Fz——加载的力；

I——矩形梁的惯量。

V型悬臂由于被认为具有更高的侧向刚度是目前探针形状里面较流行的设计[4]，但对于V型探针，不同厂家的设计形状略有不同，有些还有金属涂层。这些因素都影响悬臂的弹性常数，也造成弹性常数计算方法的不同。

维度法计算V型悬臂的方法主要有3种：1）平行光束近似法；2）复杂的分析模型；3）有限元分析法。

1.1平行光束近似法

平行光束近似法是将V型悬臂近似地看作两个矩形梁平行连接组成。Butt等[5]基于这个假设对式（1）进行改进，但是由于实际两个“矩形梁”并非平行，而是斜交的，因此计算方法会带来一定的误差，当悬臂的长L比较短且悬臂自由端成一条直线时，这种假设更加准确，但是当悬臂的长L比较长的时则Albrecht模型公式则更为准确[6]。为了让模型更加有效而准确，Sader等[7]在数学模型中引入了V型悬臂顶角2θ（如图1（a）所示）。下面列举4个最典型的平行光束近似法的简单模型公式。

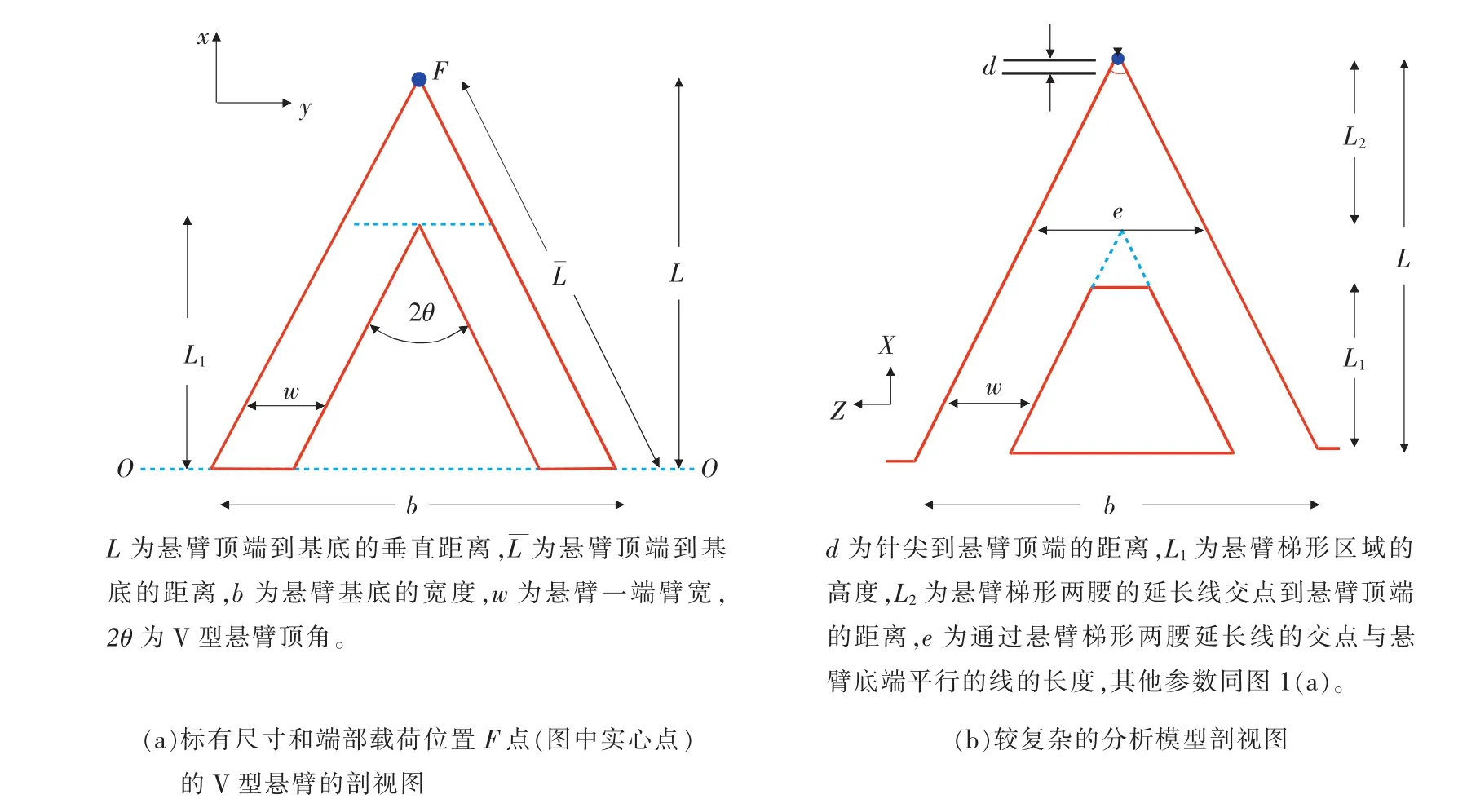
图1　V型悬臂示意图

Butt模型[5]：

Albrecht模型[6]：

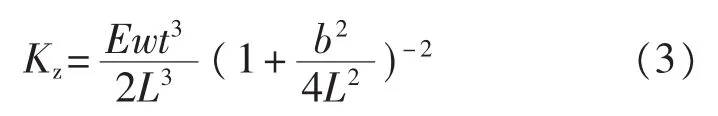
Sader模型[7]：

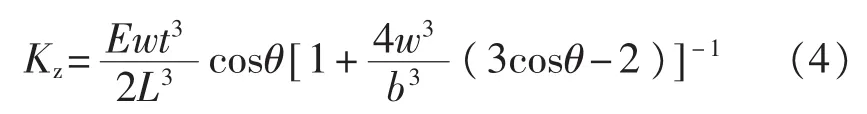
1.2复杂分析模型

复杂分析模型的中心思想是将悬臂看成两个或两个以上的形状，并且引入更多的元素。复杂模型也适用于悬臂成A字形状的探针，比如Warmack阐述的计算模型[8]如式（5）所示，模型中悬臂几何尺寸参数的意义如图1（b）所示，此计算方法需要已知悬臂尺寸、针尖的位置和杨氏模量。如果L1和针尖到悬臂顶端的距离d设定为0，则弹性常数可以简化为下式，成为简单模型。

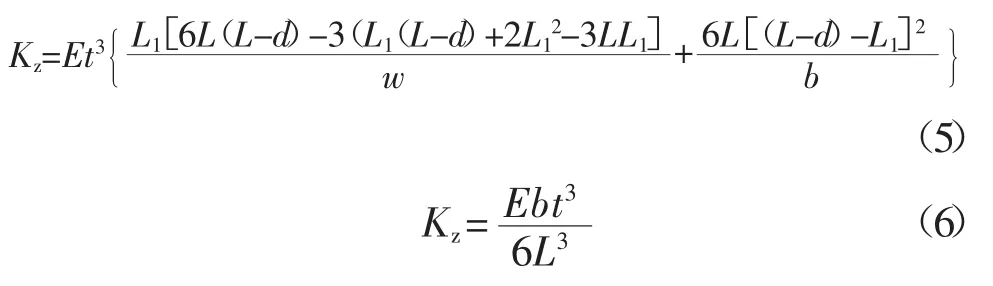
Tortonese把悬臂尖端尺寸分出如图1（b）所示的L2的区域，并标示通过悬臂梯形两腰延长线的交点与悬臂底端平行的线的长度e，引出另外一个式（7）[9]。对于一个V形悬臂（见图1（a）），该宽度等于2w。Tortonese方程同Warmack方程在当悬臂假定为V型，同时d为0时具有一致的结果。

1.3有限元分析

90年代初已有利用有限元分析（FEA）方法模拟V形悬臂的报道。这种方法要求精确知道悬臂几何形状、杨氏模量还有悬臂梁的密度。该方法的优点是简单、快速，可以将涂层与基体视为一个平均材料处理各种带有不同涂层的V形悬臂。近年对该方法的研究大多是将有限元的方法结合到其他方法中提高弹性常数的精确度[3，10]。

维度法直观明了，主要基于对探针的几何尺寸和弹性性能的测试。维度法针对直角悬臂的计算准确度较高，但对于V型、A型、梯形或者更加复杂的形状精确度不高。

2　静态挠度法

静态挠度法即参考悬臂法，主要通过准确校正一个参考悬臂，然后使用这个参考悬臂校准未知的悬臂梁，如图2[11]所示。

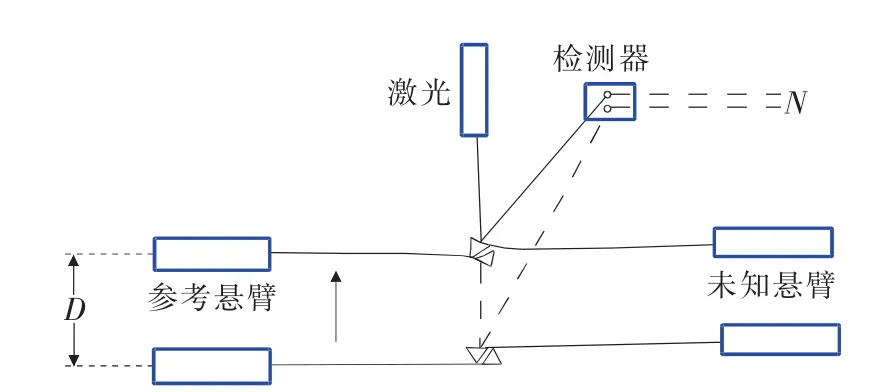
图2　参考悬臂法校正弹性常数的示意图

未知弹性常数的探针悬臂（右侧）压在已知弹性常数的参考悬臂（左侧）上，通过测定两个悬臂的偏转灵敏度，即可得出未知悬臂的弹性常数，如下式所示：

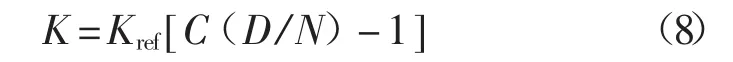
式中：Kref——参考悬臂的弹性常数；

C——nA与nm的转化系数；

D/N——在力曲线接触区域的斜率的倒数。

参考悬臂法由于其测试方法简单快速，测试结果准确性较高等优点使用广泛，近年来不断有研究人员对方法进行改进。Richard S.Gates等[12]对参考悬臂梁的外端荷载进行了修正。通过Hooke定律结合Euler-Bernoulli光束方程得到下式：

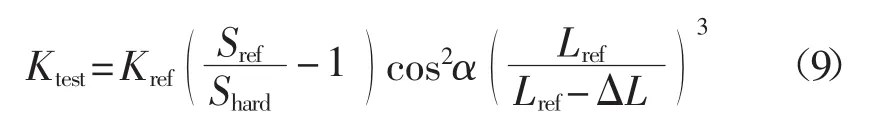
式中：Kref、L——参考悬臂的弹性常数和长度；

ΔL——端部到承载位置的距离（如图3所示）；

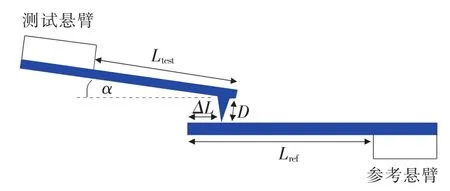
图3　Gates改进参考悬臂数学模型的参数意义

cos2α——悬臂倾斜角度的几何校正；

Sref——测试悬臂压在参考悬臂上的光杆灵敏度；

Shard——测试悬臂梁压在坚硬的表面（如硅等）的光杆灵敏度。

实际上，参考悬臂法的准确度主要依赖于参考悬臂本身弹性常数测量的准确性，因此，近年来对该方法的改进集中在提高对参考悬臂弹性常数的测量准确度上。Clifford等[13]采用纳米压痕仪首先校正参考悬臂的弹性常数，获得更加准确的参考悬臂的弹性常数值，再对未知悬臂做进一步检测，提高了本方法的准确度，其方法具体的表达式为

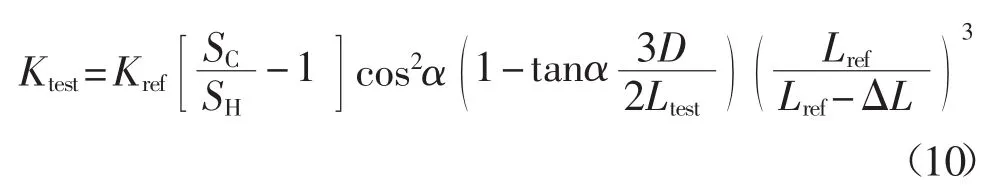
式中：SH——未知悬臂梁压在坚硬表面的光杆灵敏度；

SC——未知悬臂梁压在参考悬臂梁时的光杆灵敏度；

D——未知悬臂投影的高度（如图3所示）；

Kim等[14]把校准的悬臂连接到一个固定的支架上，支架由一个高准确度扫描仪（重力方向1nm分辨率）记录位移。悬臂被压在一个精密质量比较器的负载按钮上。将弹性压缩悬臂所产生的力再由一个电磁力补偿，从而保持负载按钮的位置。补偿力等于接触力，悬臂的弹性常数通过其位移除以电磁力来确定。悬臂的位移测量由一个电容传感器纳入扫描仪中，由激光干涉仪校准。这种被称为纳米力的校准方法可提供更加准确的测定，对MP31120探针不确定性不到1%。

Ashley D Slattery等[15]使用聚焦离子束在参考悬臂上制造小孔进行位置标记，再利用Clifford方法校正弹性常数，同样，也提高了该方法的不确定性。

3　动态挠度法

3.1Cleveland方法（附加质量法）

1993年，Cleveland[4]通过将已知质量的物质如微球等附加到悬臂的自由端，然后测量附加质量前后共振频率的变化获得弹性常数。其弹性常数的计算为

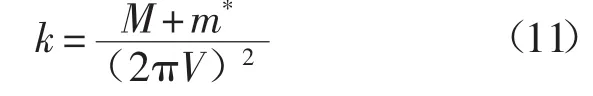
式中：m*——有效的悬臂质量；

M——附加在悬臂末端的质量；

V——悬臂的共振频率。

如果测量得到空载谐振频率V0及附加质量M1的谐振频率V1，则可以根据已知得到质量、频率、弹性常数的关系方程：

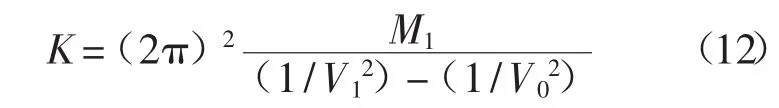
式（12）还可以转变为弹性常数与悬臂尺寸、密度、模量和谐振频率的关系式：

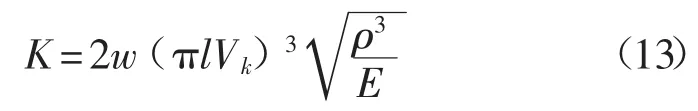
式中：w——悬臂梁的宽度；

l——悬臂梁的长度；

Vk——谐振频率；

ρ——悬臂密度；

E——弹性模量。

利用Cleveland计算方法推导出的扭转弹性常数的计算式[16]为

式中：KΦ——扭转弹性常数；

ωt——扭转共振频率；

Je——有效的质量矩。

并得到当附加物为球型时的扭转弹性常数的计算公式：

式中ρs和r分别为附加物的密度与半径。

3.2Sader方法

Sader方法[17]是通过在已知密度和粘度的流体场（如空气）中微悬臂梁振动的谐振响应过程中加入流体耗散效应计算弹性常数的方法。对于直角悬臂，有：

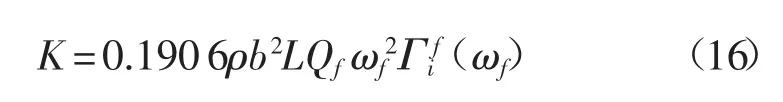
式中：L、b——悬臂的长和宽；

ρ——流体的密度；

ωf——径向的振动频率；

Qf——谐振峰的品质因子；

Γi——流体函数的虚部。

Γi是雷诺兹数Re的函数。悬臂的谐振频率ω和品质因子Q值可以通过悬臂热驱动的振荡功率谱密度分析得到，基本功率谱共振峰通过拟合一个简谐振子的响应加白噪声基底得到[18]，其计算表达式为

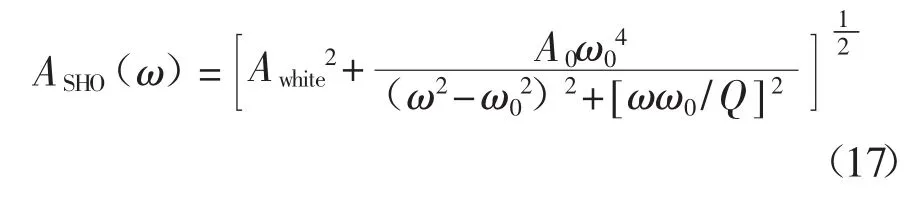
式中：Awhite——白噪声基底振幅；

A0——零频率振幅；

ω0——无耗散效应的谐振频率；

Q——品质因子。

Sader等将Sader方法进行拓展，推导出了Sader扭转弹性常数的公式：

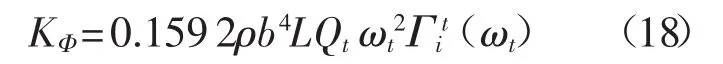
经实验验证，Sader扭转弹性常数公式与Cleveland扭转弹性常数公式计算结果高度一致[16]。

Sader等[19-21]最近还提出了对Sader公式的简化。简化方法仅依靠悬臂的共振频率和品质因数，不需要测量悬臂梁的动力学性能，更加省时实用。经过验证，该简化方法同样准确、快速。

Sader还在网站上（http://www.ampc.ms.unimelb. edu.au/afm/calibration.html）提供了一个Java小程序，只要输入悬臂的长度和宽度，适当的谐振频率和相应的质量因子，按计算按钮，就可以自动执行计算，在线校正弹性常数。

3.3热噪音法

热噪音（或称热调谐、热振动）法是目前最流行和最广泛使用的方法之一。Vecco公司所有使用V型控制器的系统都用热噪音法进行校正。热噪音法是根据分子热运动理论，把悬臂梁近似等效成理想弹簧，悬臂当作一个简单的谐波振荡器，测量微悬臂梁的位移随着时间的变化，通过微悬臂处于热平衡状态时的热噪音谱，获得弹性常数与温度、噪声谱之间的关系，从而求出微悬臂的法向弹性常数[22]。

热噪音法的基本数学模型公式为

式中：KB——波尔兹曼常数（1.38×10-23J/K）；

T——绝对温度；

〈Zc2〉——悬臂位移的均方根。

考虑到悬臂不是理想弹簧，他们振荡模式的能量不同于一个简单的谐波振荡器。所以引入校正因子，公式变为

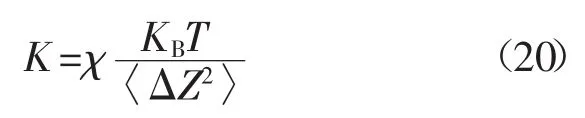
式中：〈ΔZ2〉——悬臂自由端位移的均方根；

χ——校正因子。

校正因子依赖于探针悬臂的形状和激光聚焦在悬臂上面的位置[23-24]。

为了提高探针与样品间的距离，原子力显微镜的悬臂通常安装在与水平有很小角度的位置。校准的弹性常数往往由于倾斜低估一个cos2α因素（这里α为相对水平倾斜角度，通常约12°）。如果没有适当的修正，可能会导致在力的测量上的错误。研究发现，对于参考悬臂和热调谐方法，无需进一步校正。维度法，附加质量法和Sader方法，需要进一步校正，得到有效的弹性常数，校正公式为

4　探针弹性常数校正方法的选择

综上所述，以上所有的校正方法，都有各自模型特点。总结现已发表的弹性常数校正方法的优缺点与不确定度如表1所示。对于相对刚性的（即K＞1N/m）矩形悬臂，Sader方法更加适合，该方法的不确定度良好，测量方便。参考悬臂法也是不错的选择，但它操作不够友好，对探针的损耗大，通常会带来更多的不确定性。相对柔软的悬臂（即K＜1N/m），热调谐法则更适合也很简便，不确定性相对较低。而对于柔软的V形悬臂，Sader方法则不适用，参考悬臂法则是不错的选择。

表1　已发表的弹性常数校正方法的优缺点与不确定性的概述

结合笔者所在实验室目前使用较多的探针类型和测试仪器型号（Bruker Multimode 8），在考虑已知悬臂参数的情况下，可采用的方法如表2所示。当然，在进行弹性常数校正实验的实际操作中，不仅要考虑探针悬臂本身的实际情况（形状、尺寸、已知参数等条件），还要考虑每种方法执行的难易程度；同时，选用的方法其误差大小是否在可以接受的范围也需要事先考虑清楚；当然，实验人员对哪种方法运用更熟练也是非常重要的因素。

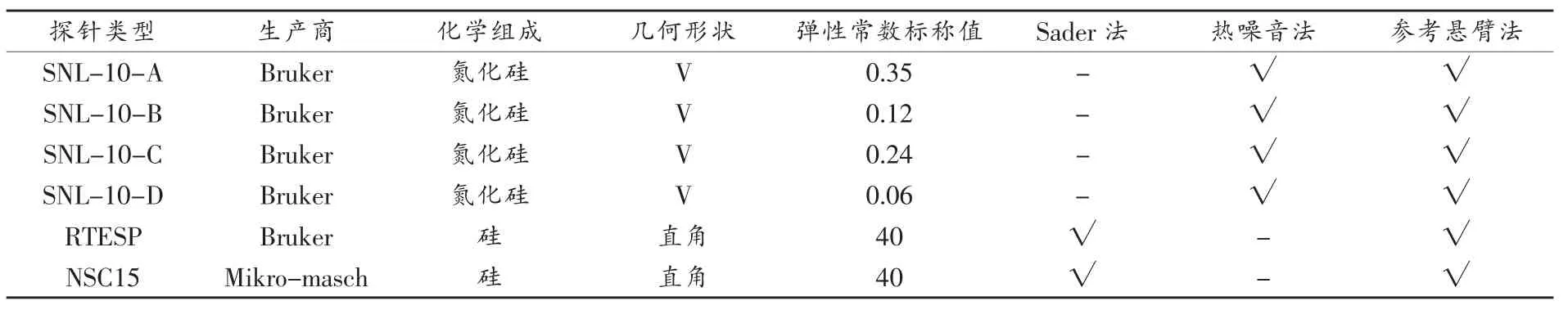
表2　不同类型探针弹性常数校正方法的选择

5　结束语

通过借助一些额外的设备，如电子或光学显微镜等，原子力显微镜探针悬臂的弹性常数获得了更为准确的表征。随着这些辅助测量仪器的精密度的提高，弹性常数校正方法的准确程度也必将不断提高。对于今后弹性常数校正的研究，不仅需要对校正方法准确度的提高进行研究，还应该对校正方法进行不断的简化[20-21]，追求更加精确、先进的校正方法。

[1]RAMAN A，TRIGUEROS S，CARTAGENA A，et al. Mapping nanomechanical properties of live cells using multi-harmonic atomic force microscopy[J].Nature Nanotechnology，2011（6）：809-814.

[2]STAN G，SOLARES S D，PITTENGER B，et al.Nanoscale mechanicsbytomographiccontactresonanceatomic force microscopy[J].Nanoscale，2014（6）：962-969.

[3]GEORGAKAKID，MITRIDIS S，Sapalidis A A，et al. Calibration of tapping AFM cantilevers and uncertainty estimation：Comparisonbetweendifferentmethods[J]. Measurement，2013（46）：4274-4281.

[4]CLEVELAND J P，MANNE S，BOCEK D，et al.A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy[J].Rev Sci Instrum，1993（64）：403-405.

[5]BUTT H，SIEDLE P，SEIFERT K，et al.Scan speed limit in atomic force microscopy[J].J Micro，1992（169）：75-84.

[6]ALBRECHT T R，AKAMINE S，CARVER T E，et al. Microfabrication of cantilever styli for the Atomic Force Microscope[J].J Vac Sci Tech，1990（8）：3386-3396.

[7]SADER J E.Parallel beam approximation for V-shaped atomic force microscope cantilevers[J].Rev Sci Instrum，1995（66）：4583-4587.

[8]WARMACK R，ZHENG X Y，THUNDAT T，et al. Friction Effects in the Deflection of Atomic Force Microscope Cantilevers[J].Rev Sci Instrum，1994（65）：394-399.

[9]TORTONESE M.Cantilevers and tips for atomic force microscopy[J].IEEE Eng Med Bio，1997（16）：28-33.

[10]CHOI J L，GETHIN D T.Simulation of atomic force microscopy operation via three-dimensional finite element modelling[J].Nanotechnology，2009（20）：1-14.

[11]GIBSON C T，WATSON G S，MYHRA S.Determination of the spring constants of probes for force microscopy/ spectroscopy[J].Nanotechnology，1996（7）：259-262.

[12]GATES R S，REITSMA MARK G.Precise atomic force microscope cantilever spring constant calibration using a reference cantilever array[J].Rev Sci Instrum，2007（78）：086101-3.

[13]CLIFFORD C A，SEAH M P.Improved methods and uncertainty analysis in the calibration of the spring constant of an atomic force microscope cantilever using static experimental methods[J].Meas Sci Technol，2009（20）：125501-10.

[14]KIM M S，CHIO J H，KIM J H，et al.Accurate determination of spring constant of atomic force microscope cantilevers andcomparison with other methods[J].Measurement，2010（43）：520-526.

[15]SLATTERY A D，BLANCH A J，QUINTON J S，et al. Calibration of atomic force microscope cantilevers using standard and inverted static methods assisted by FIB-milled spatial markers[J].Nanotechnology，2013（24）：015710-13.

[16]GREEN C P，LIOE H，CLEVELAND J P，et al.Normal andtorsionalspringconstantsofatomicforce microscope cantilevers[J].Rev Sci Instrum.，2004（75）：1988-1995.

[17]SADER J E，CHON J W M，MULVANDY P.Calibration of rectangular atomic force micro scope cantilevers[J]. Rev Sci Instrum，1999（70）：3767-3969.

[18]PIRZER T，HUGEL T.Atomic force microscopy spring constant determination in viscous liquids[J].Rev Sci Instrum，2009（80）：035110-6.

[19]SADER J E，SANELLI J A，ADAMSON B D，et al. Spring constant calibration of atomic force microscope cantilevers of arbitrary shape[J].Rev Sci Instrum，2012（83）：103705-16.

[20]SADER J E，FRIEND J R.Calibration of atomic force microscopecantileversusingonlytheirresonant frequency and quality factor[J].Review of Scientific Instruments，2014（85）：116101-3.

[21]SLATTERY A D，BLANCH A J，EJOV V.Spring constant calibration techniques for next-generation fastscanningatomicforcemicroscopecantilevers[J]. Nanotechnology，2014（25）：335705-13.

[22]SADER J E，LU J，MULVANEY P.Effect of cantilever geometry on the optical lever sensitivities and thermal noise method of the atomic force microscope[J].Rev Sci Instrum，2014（85）：113702-6.

[23]PROKSCH R，SCHAFFER T E，CLEVELAND J P，et al. Finiteopticalspotsizeandpositioncorrectionsin thermal spring constant calibration[J].Nanotechnology，2004（15）：1344-1350.

[24]SCHAFFER T E.Calculation of thermal noise in an atomic forcemicroscopewithafiniteopticalspotsize[J]. Nanotechnology，2005（16）：664-670.

（编辑：徐柳）

Research progress on the calibration methods for elastic constant of atomic force microscopy cantilevers

QU Zehua，BU Juan，PAN Xiaoxia
（State Key Laboratory of Molecular Engineering of Polymers，Department of Macromolecular Science，Fudan University，Shanghai 200433，China）

It’s vital to know exactly the elastic constant of the cantilever of an atomic force microscope before the mechanical properties of material surfaces are quantitatively characterized with this device.This paper has reviewed corresponding calibration methods used in recent years，comprising dimensional method，static deflection and dynamic deflection.The dimensional method is designed for expounding different cantilever shapes（mostly rectangular and V-shaped），the mathematical models and their advantages and disadvantages of different methods will be analyzed in this paper.The static deflection is used to explain the mathematical models and the study on the accuracy improvement of these methods particularly.The dynamic deflection is reviewed separately with three approaches namely added mass method，Sader method and thermal tuning method.The model characteristics and advancement of the three methods are compared here.In the end，several suitable calibrations also be discussed for common cantilevers;the research prospect of these calibration methods are proposed.

cantilever；elastic constant；calibration；summary

A

1674-5124（2016）03-0001-06

10.11857/j.issn.1674-5124.2016.03.001

2015-09-18；

2015-11-19

聚合物分子工程国家重点实验室仪器类开放课题（KVH1717101/001/018）

屈泽华（1978-），女，吉林九台市人，博士，主要从事原子力显微镜、扫描电镜相关研究工作。