不同晶体时间响应参数对脉冲辐射测量统计涨落影响评估

郭洪生，张建华，杨高照，朱学彬，胡青元

（中国工程物理研究院核物理与化学研究所，四川 绵阳 621900）

不同晶体时间响应参数对脉冲辐射测量统计涨落影响评估

郭洪生，张建华，杨高照，朱学彬，胡青元

（中国工程物理研究院核物理与化学研究所，四川 绵阳 621900）

为评估不同时间响应参数的无机晶体所造成的统计涨落对零功率堆瞬发中子时间常数α测量结果的影响，构建数值模型对其进行计算。结果表明：原本为负常数的α曲线，经过不同时间响应参数的晶体卷积后，α值由常数变成曲线；且在时间零点附近急剧变化，甚至出现正数值；晶体时间响应参数越大，偏离α值越多；对于不同的晶体，时间零点附近α值变化区间不一样，慢晶体的变化区间最长。

零功率堆；瞬发中子时间常数；无机晶体；时间响应参数；统计涨落

0　引　言

任何一个放射性测量，即使所有测量条件都是稳定的，每次测量结果也并不完全相同，而是围绕某个平均数值上下涨落，这种现象称为放射性测量的统计涨落。这种涨落并非由测量条件变化引起，而是微观粒子运动过程中的一种规律性现象，由放射性测量的随机性造成。

零功率堆瞬发中子时间系数α，对于反应堆核安全分析、核材料加工存储以及加速器驱动次临界系统研究等多方面的应用都有重要意义，是反应堆物理研究中的重要参数。基于高强度、短脉冲瞬态中子源[1]（DPF）的瞬态测量方法[2]较成熟的传统测量方法具有费时短、准确度高等优点，该方法所采用的探测系统由光电倍增管（PMT）与无机闪烁晶体组成，系统中光电倍增管的时间常数约为1～2 ns，所引起的统计涨落效应可以忽略，而无机闪烁晶体的时间常数从数ns到数百ns不等，所引起的统计涨落效应对相应测量结果的影响不同。本文针对上述问题构建了数值模型进行计算评估。

1　测量原理

在反应堆物理研究中，零功率堆瞬发中子时间系数α是零功率堆系统动力学行为的重要物理特征量，对于反应堆核安全分析、核材料加工存储以及加速器驱动次临界系统研究等多方面的应用都有重要意义[1-2]。近年来，伴随脉冲功率和气体放电技术的不断进步，发展了高强度（～1010n/pulse，D-T中子）、窄脉冲（～30ns）中子源（DPF）[3]，并在此基础上研发了零功率堆瞬发中子时间系数α的瞬态测量方法[4]。该方法较Rossi-α法、方差平均比方法、零几率法、时间间隔分布法、252Cf随机脉冲源法等传统测量方法具有费时短、准确度高等优点。

零功率堆中子时间系数α的瞬态测量方法原理[5]为：在DPF强中子源照射下，零功率堆装置出射的γ射线经过准直器直接作用于对γ射线灵敏的探测器上，该探测器由对γ射线灵敏、对中子相对不灵敏的无机闪烁体和光电倍增管组成（ST-PMT系统），该探测系统具备荧光衰减时间短和灵敏电荷放大能力高等优点。探测器输出脉冲电流信号，该信号经射频电缆传输至示波器记录（如图1所示），数据处理后得到中子时间系数α。在探测器动态范围内，测量系统是线性的，探测器的输出电流i（t）与零功率堆的γ射线时间谱N（t）成正比。

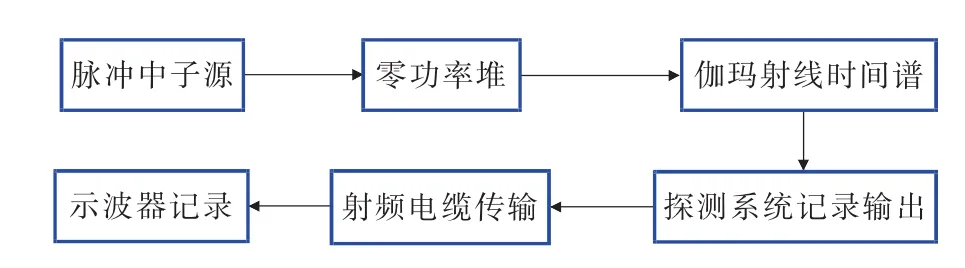
图1　瞬发中子时间系数α测量原理

2　数学模拟

在核粒子测量和脉冲辐射场测量中，不论是测量记录的粒子数目，还是记录粒子所致的电荷量，即使测量条件不变，测量系统工作状态保持稳定，每次测量值总是在某个值的水平上下波动[6]。这种波动是由辐射粒子数目及其所致的次级效应的统计性造成的，谓之统计涨落。脉冲辐射场测量中，表现出的统计性是群粒子（量子）集体行为的统计平均性，既有记录粒子数目的统计涨落，又有群粒子总作用效果的统计涨落。因为零功率堆中子时间系数α的测量也属于脉冲辐射场测量范畴，统计涨落对测量结果也将产生影响。为了模拟统计涨落对中子时间系数α瞬态测量的影响，依据上述测量原理，人为构造一个中子衰减系数输入函数I（t）（相当于图1中的第4个环节，即探测器记录由零功率堆放出的γ射线时间谱），是一个常负指数型脉冲信号。设定零功率堆系统参数（质量、密度、平均每次裂变放出光子数等），DPF中子源参数（产额、半宽度、距离、类型（D-D/D-T）、入射到零功率堆时间等）及探测系统参数（响应函数、探测效率、面积、距离、屏蔽系数等），由设定的参数出发对探测系统的输出信号进行模拟计算。计算依据的公式[7-8]为

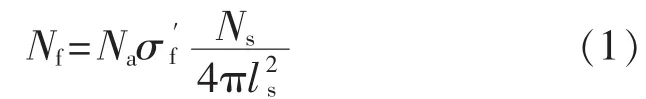
式中：Nf——DPF源中子在零功率堆中引发的直接

裂变数；

Na——裂变核总数；

σf——源中子裂变截面；

Ns——中子源中子产额；

ls——中子源至零功率堆心的距离。

式中：C——将中子源看作δ时由源中子直接裂变

产生的增长引起的裂变速率；

νn——平均每次源中子裂变产生中子数；

na——裂变核的数密度；

<σ·ν>——裂变截面σ与中子速度ν之积

在裂变中子谱上的平均值。

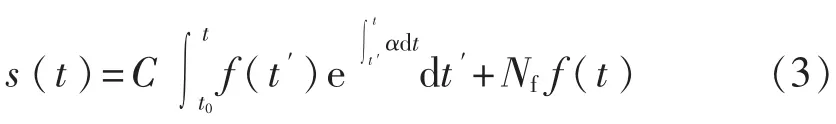
式中：s（t）——t时刻零功率堆系统的裂变速率；

t0——源中子开始注入时间；

f（t）——源中子归一化时间分布曲线；

α——零功率堆中子时间系数。

式（3）中的第2项表示源中子直接裂变的裂变速率，第1项为经系统增值的裂变速率。显然，当α为负无穷大时，第1项趋近于0。

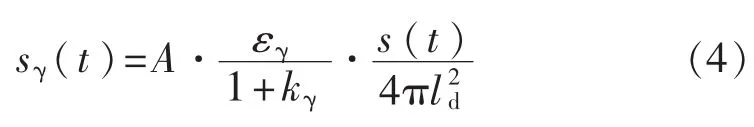
式中：sγ（t）——t时刻单位时间里探头记录到的光子数；

A——探头对着零功率堆装置心的横截面；

εγ——探头的探测效率；

kγ——对γ的屏蔽系数；

ld——探头到零功率堆装置心的距离。

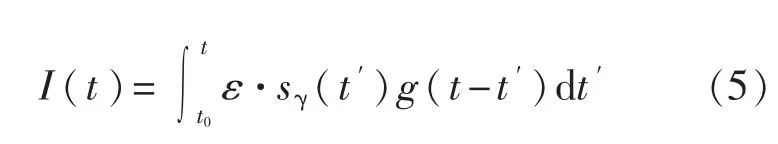
式中：I（t）——探头输出的平均信号曲线；

ε——平均每个光子沉积在探头中的能量；

g（t）——探头的响应曲线。

中子时间系数α的求取由信号曲线按下式进行：

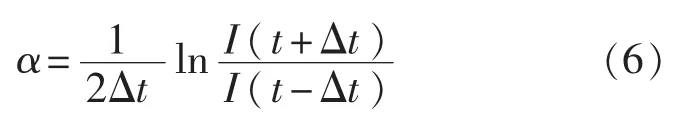
3　数学卷积

在物理测量中，探测器由光电倍增管（PMT）和对γ射线相对灵敏、对中子相对不灵敏的无机晶体组成。γ光子入射到无机晶体表面转换成光电子入射到光电倍增管内经倍增放大输出电信号并由电缆传输至示波器记录。

设模拟获取的输入I（t）为指数信号，I（t）由第2节给出，探测器响应为g（t），由：

利用卷积公式：

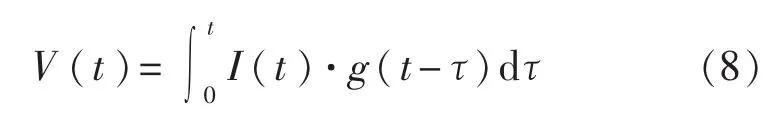
可获得输出V（t）（相当于图1中的第4到第5个环节）。将V（t）按上述给定方法计算α，即可考察探测器对α的畸变；如果在式（7）中加上某种统计涨落，再按上述方法处理，则可知道在这种情况下探测器和该种统计涨落对常数α测量的影响。

4　统计涨落的数值模拟

设在示波器上所记录的波形如式（7）所示，利用公式：

可得到在（a，b）上满足某种分布（如均匀分布）的随机数xi+1。

由ti=（i-1）Δt i=1，2，…，按上式计算ti上的值νi，于是有：

得到一种带随机涨落的信号幅度数据。若将波形幅度值νi乘以系数K：

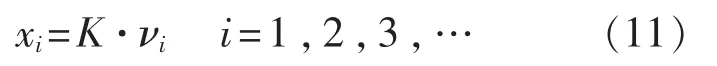
并随机取定xi的符号，利用式（11）可获得另一种带随机涨落的信号幅度数据，这里K为小于1的任意实数。

当式（11）中xi的符号严格按一正一负的方法确定时，可得到正负相间的一种统计涨落的信号幅度数据[9]。可以看出，用数值方法模拟统计涨落的方法很多，具体运用时主要看模拟结果是否符合实际测量情况。

时间特性不同的晶体对α系数测量的影响不同，使用不同晶体时产生的统计涨落可能也各不相同。为方便起见，不论涨落的产生机制如何，都归结为记录信号带统计涨落。一般的，实验时采用无机晶体，其响应函数为

利用式（8）即可得出时间特性不同的晶体对α测量的影响。

令式（7）中N0=1，β=5，α=-4μs-1，晶体时间响应参数T1=0.1ns，T2分别取值5，50，200 ns。卷积后再计算α值，可得到表1中的结果。从表中可看出：晶体时间常数T2值越小，受统计涨落影响越小，随着测量结果所取时间段变长，测量结果越接近真值。

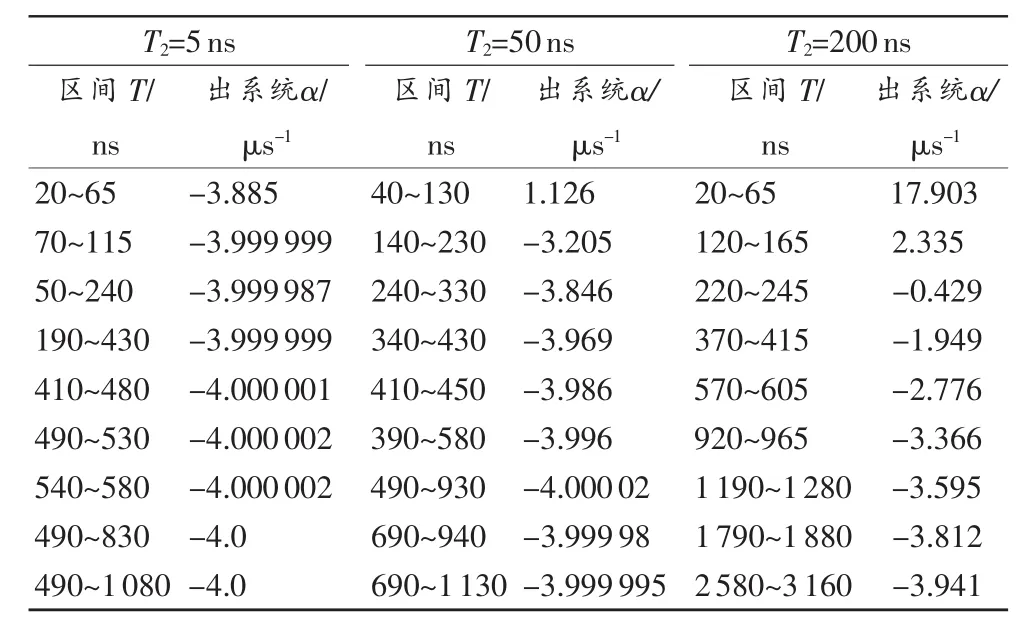
表1　不同晶体（T1=0.1ns）对α测量的影响

5　结束语

从上述数值模拟可看出，原本的输入函数α=-4μs-1，经过不同时间常数的晶体卷积后，有如下特点：

1）α的图形由直线变成了曲线；

2）在时间零点附近 α值急剧变化，非但不等于-4，甚至出现了正值；

3）时间常数T2越大，偏离α值越多；

4）对于不同的晶体，时间零点附近α值不断变化的区间不一样，慢晶体的变化区间最长，这是晶体发光上升时间造成的畸变。

经分析，入射光子在晶体中产生统计涨落的原因为：1）即使光子与物质相互作用的主要机制是康普顿效应，它所产生的次级电子能量随出射角度不同而变化；2）闪烁体体积有限，有一部分次级电子的射程会超出闪烁体之外，而这部分份额与闪烁体的体积、形状以及光子与原子发生相互作用的地点有关；3）闪烁体不可能把发出的可见光全部耦合到光阴极上；4）闪烁体内部的不均匀性、光电倍增管光阴极各部分的量子效率不均匀性都会引起统计涨落。

实验结果的数据处理所选时间段通常为光子衰减一个量级的时间[10]，当α=-4 μs-1时，光子衰减一个量级的时间为575 ns，从表1中可看出，当取值为575ns时，对于晶体时间常数为5，50，200ns时的出系统 α值分别为：-4.000 002，-3.996，-2.776 μs-1，它们与真值α=-4 μs-1的差别分别为：0.000002，0.004，1.224μs-1。目前常用的无机晶体主要有：CeF3（T2=20ns），Yb∶YAG（T2=3ns），Ce∶YAG（T2= 50ns）和NaI（Tl）（T2=230ns）。为避免探测器晶体对测量结果造成的影响，实际测量时不能选用太慢的晶体（当α=-4μs-1时宜选用时间常数小于50ns的晶体），否则必须首先消除测量系统对结果的畸变。

[1]刘庆兆，赵毓武，陈冠宇，等.脉冲辐射场诊断技术[M].北京：科学出版社，1994：436-456.

[2]复旦大学，清华大学，北京大学.原子核物理实验方法（上册）[M].北京：原子能出版社，1985：253-261.

[3]郭洪生.DPF中子产生机制和中子参数测量技术研究[Z].中国工程物理研究院年报.绵阳：中国工程科学研究院科技年报编辑部，2003.

[4]郭洪生.静态次临界装置衰变常数的瞬态测量方法[Z].中国工程物理研究院年报.绵阳：中国工程科学研究院科技年报编辑部，2003.

[5]汲长松.核辐射探测器及其实验技术手册[M].北京：原子能出版社，1990：317-324.

[6]安继刚.电离辐射探测器[M].北京：原子能出版社，1995：19-27.

[7]吕敏.脉冲辐射束测量中的统计起伏问题[J].物理学报，1983，32（2）：216.

[8]陈元金.脉冲辐射场测量数据处理与误差分析[M].北京：国防工业出版社，1997：88-114.

[9]冯康，张建中，张绮霞，等.数值计算方法[M].北京：国防工业出版社，1978：147-152.

[10]张世英，刘智敏.测量实践的数据处理[M].北京：科学出版社，1977：484－491.

（编辑：刘杨）

Effects evaluation of pulsed radiation measurement statistical fluctuation caused by time responses of scintillators

GUO Hongsheng，ZHANG Jianhua，YANG Gaozhao，ZHU Xuebin，HU Qingyuan
（Institute of Nuclear Physics and Chemistry，CAEP，Mianyang 621900，China）

Different time responses of scintillators result in different fluctuation in pulsed radiation measurement which play great influence on the measurement of time constant α of zero power assembly.Mathematical models are established to evaluate the influence in this paper.Results show that the initial negative constant values of α turns to curves due to convolution of different time responses of scintillators.Values of α changes drastically and there are even positive values of α.The slower the time reoponse is，the more deviation of α.Especially，the time variation section of α changes differently around the zero point of time axis for different scintillators.The time variation section of α is the longest for the slowest time response of scintillators.

zero power reactor；instant neutron time constant；inorganic scintillator；time response parameter；statistical fluctuation

A

1674-5124（2016）03-0021-03

10.11857/j.issn.1674-5124.2016.03.005

2015-05-30；

2015-07-17

郭洪生（1961-），男，福建龙岩市人，研究员，研究方向为强脉冲辐射测量。