基于试验模态法的五轴水射流机床动态特性研究

余西伟，张仕进，张　祥，曾令亮，章伟成

（上海大学 机电工程与自动化学院，上海 200072）

基于试验模态法的五轴水射流机床动态特性研究

余西伟，张仕进，张祥，曾令亮，章伟成

（上海大学 机电工程与自动化学院，上海 200072）

基于试验模态分析理论，运用力锤激励法对五轴联动水射流机床整机进行单点激励（SISO）结构模态试验；结合响应信号，构建试验模态分析系统，获得了整机结构的低阶固有频率、阻尼比和相应的模态振型，并通过模态置信准则（MAC）进行验证；通过振动试验分析可知，机床第一、二、三阶振型为其主要振动，并找出其了振源，提出了相应的措施，以降低振动。

试验模态分析；动态特性；机床振动试验；模态置信准则（MAC）

0　引言

随着五轴联动水射流机床在机械加工领域应用的日趋广泛，水射流机床由于振动引起的误差也越来越受到人们的关注。由上海狮迈科技有限公司生产的LTJ1613-5B型五轴联动智能水刀切割加工的零部件如图1所示。在没有振动的切割环境下，零件切割表面非常光滑（见图1a） ；在切割过程中机床发生振动，会导致零件的加工表面较为粗糙，严重影响被加工零件的使用（见图1b）。针对上述振动现象，学者们对机床进行振动测试，分析造成该振动现象产生的原因，并提出改进措施［1］。

试验模态分析就是研究机械振动的重要方法之一［2］。曹文平等［3］采用锤击脉冲激励法和变时基采样方法对五轴联动铣床进行试验模态分析，并提出了提高机床整体结构动态特性的方法；葛双好等［4］基于模态分析理论和模态测试技术，研究了机床进给系统的动态特性，并提出改进措施；禇志刚等［5］分别采用最小二乘复指数法和最小二乘复频域法识别模态参数，再对机床进行模态试验，得到准确的低阶固有频率、阻尼比和模态振型后，提出改进措施，以提高机床的加工精度稳定性和抗振性；魏要强等［6］提出了一种新的试验模态分析方法，以机床运动本身产生的振动为激励源，获得结构的动态特性参数，再结合基于响应信号的模态参数识别方法，去除模态参数中的伪模态，该方法可对大型重型难激励数控机床的结构动态特性进行研究。

图1　水射流切割零件Fig. 1　Water-jet cutting parts

本文针对水射流机床加工过程中的振动现象，运用力锤激励法对LTJ1613-5B型五轴联动智能水刀进行单点激励模态试验，并采用单参考点正交多项式法进行模态参数识别。在此基础上，结合机床振动试验分析机床动态特性，找出振源并提出具有可行性的减振措施［7］。

1　机床模态试验

1.1振动测试平台搭建

试验以LTJ1613-5B型五轴联动智能水刀为研究对象，结合MI-7008型数据采集分析仪（忆恒科技生产）、3263A3型压电式三向加速度传感器（美国Dytran公司生产）和5850A型力锤（美国Dytran公司生产）以及联想笔记本电脑搭建图2所示振动测试平台。

模态试验原理如图3所示。试验以力锤为激励源，采用单点激励法对机床样机进行激励，并使用压电式三向加速度传感器采集振动响应信号， 然后通过相干函数、自功率谱等对试验结果进行校验，最后对合理的试验数据进行分析。

图2　振动测试分析平台Fig. 2　Analysis platform for vibration tests

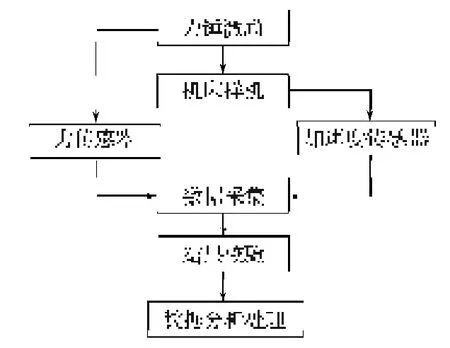
图3　模态试验原理图Fig. 3　Schematic diagram of modal experiments

1.2采样频段选择

根据香农采样定理，为了不失真地恢复模拟信号，采样频率应该不小于模拟信号频谱中最高频率的2倍，采样后的离散信号频谱才不会出现混频现象［8］。在本次振动测试中，力锤激励信号为脉冲信号，具有很高的峰值，因此，较高的采样频率才可以实现精确采样。由于试验主要关注的是机床低频阶段的振动，故本文采用变时基采样方法，以高频采集激励信号，以低频采集响应信号。因此，机床分析频段选为0～1 200 Hz，压电式三向加速度传感器的采样频率选为2 400 Hz。

1.3结构建模及布点

在模态分析中，测点数量、测点位置、测点方向的选择至关重要，既要体现出结构的特征，又要保证所关心的关注点都在测试点范围之内。与传统刀具切削过程相比，水射流切割过程中，喷嘴不与工件直接接触，无切削应力出现，但是，高速射流对机床会产生较大的反冲击作用，故本次试验主要关注机床本体的振动特性。根据其工作特性，选取154个响应点，建立测振模型，如图4所示。

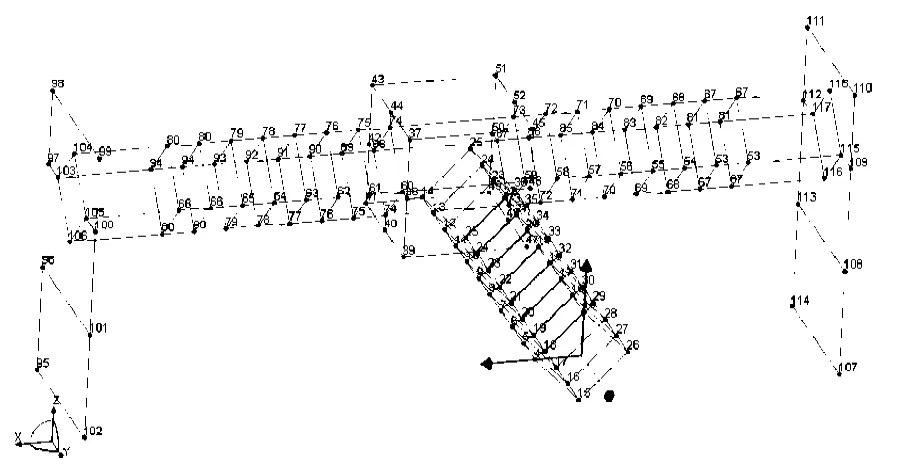
图4　测振模型Fig. 4　A vibration test model

1.4模态测试结果

通过模态试验得到154个响应点的频响函数，再采用单参考点正交多项式法进行模态参数识别，得到整机的前6阶固有频率和阻尼比。表1为前6阶的固有频率和阻尼比。

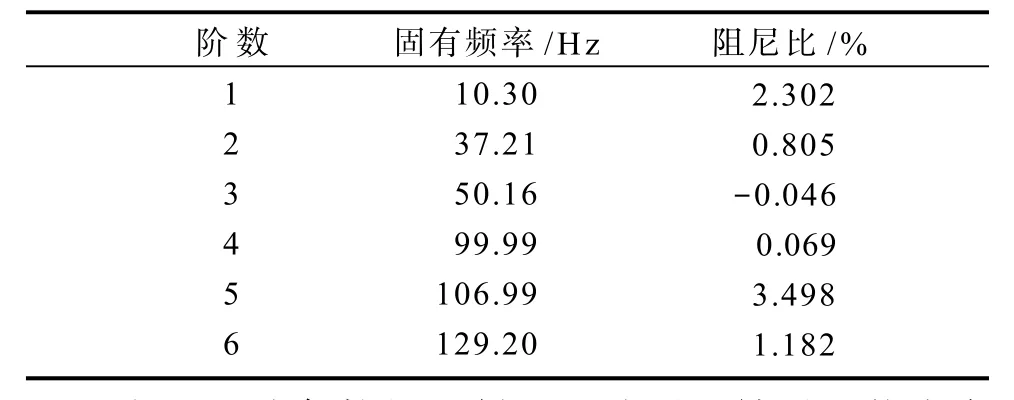
表1　前6阶固有频率和阻尼比Table 1　Inherent frequency and damping ratio of the former 6 ranks

由于试验条件的限制，试验测试结果可能会产生误差，因此，需要对模态测试结果进行评估，验证试验数据的准确性。模态置信准则（modal assurance criterion，MAC）是常用的模态验证方法之一，可对模态振型的一致性进行验证，评估两个模型模态之间的相关性。模态置信准则的校验公式为：

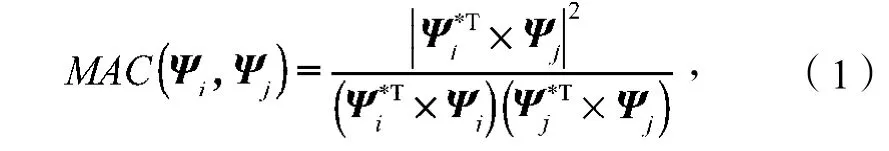
本次试验的模态置信校验如图5所示。

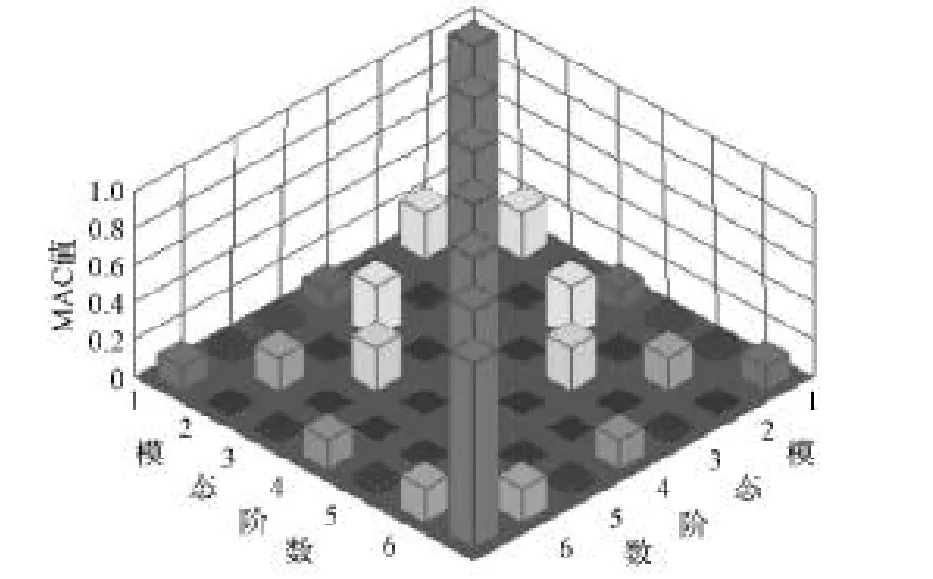
图5　模态置信校验图Fig. 5　Check diagram of the modal assurance

由图5可以得到如下结论。

1）当i=j时，MAC值等于1，说明每一阶模态振型与本身完全相关。

2）当i≠j时，大部分MAC值接近于0，说明计算得到的模态振型具有很好的正交性，每一阶模态振型与其他阶不相关。

因此，根据正交性原理可知，本次模态测试及其数据处理结果是可靠的。

1.5振型描述与分析

由模态参数识别得到前6阶固有频率所对应的模态振型如图6所示（水平轴为x轴，法向轴为y轴，竖直轴为 轴）。第一阶固有频率为10.30 Hz，振型为整机x轴正向摆动，且悬臂梁摆动幅度较大；第二阶固有频率为37.21 Hz，振型为整机x轴正向摆动，悬臂梁x负向摆动；第三阶固有频率为50.16 Hz，振型为悬臂梁轴负向摆动；第四阶固有频率为99.99 Hz，振型为悬臂梁绕y轴扭转；第五阶固有频率为106.99 Hz，振型为悬臂梁x轴正向大幅度摆动；第六阶固有频率为129.20 Hz，振型为横梁向 轴正向摆动，悬臂梁中间部位向 轴负向摆动。

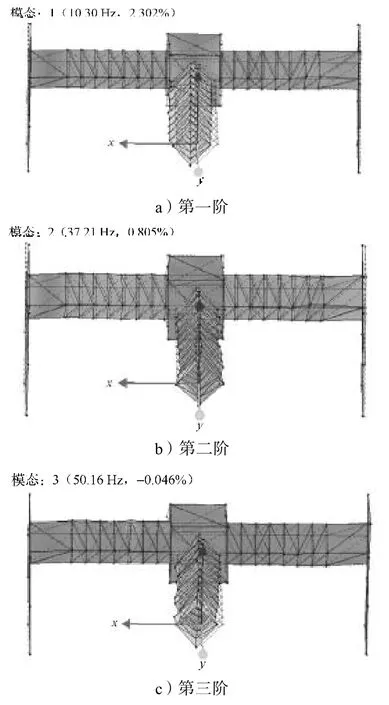
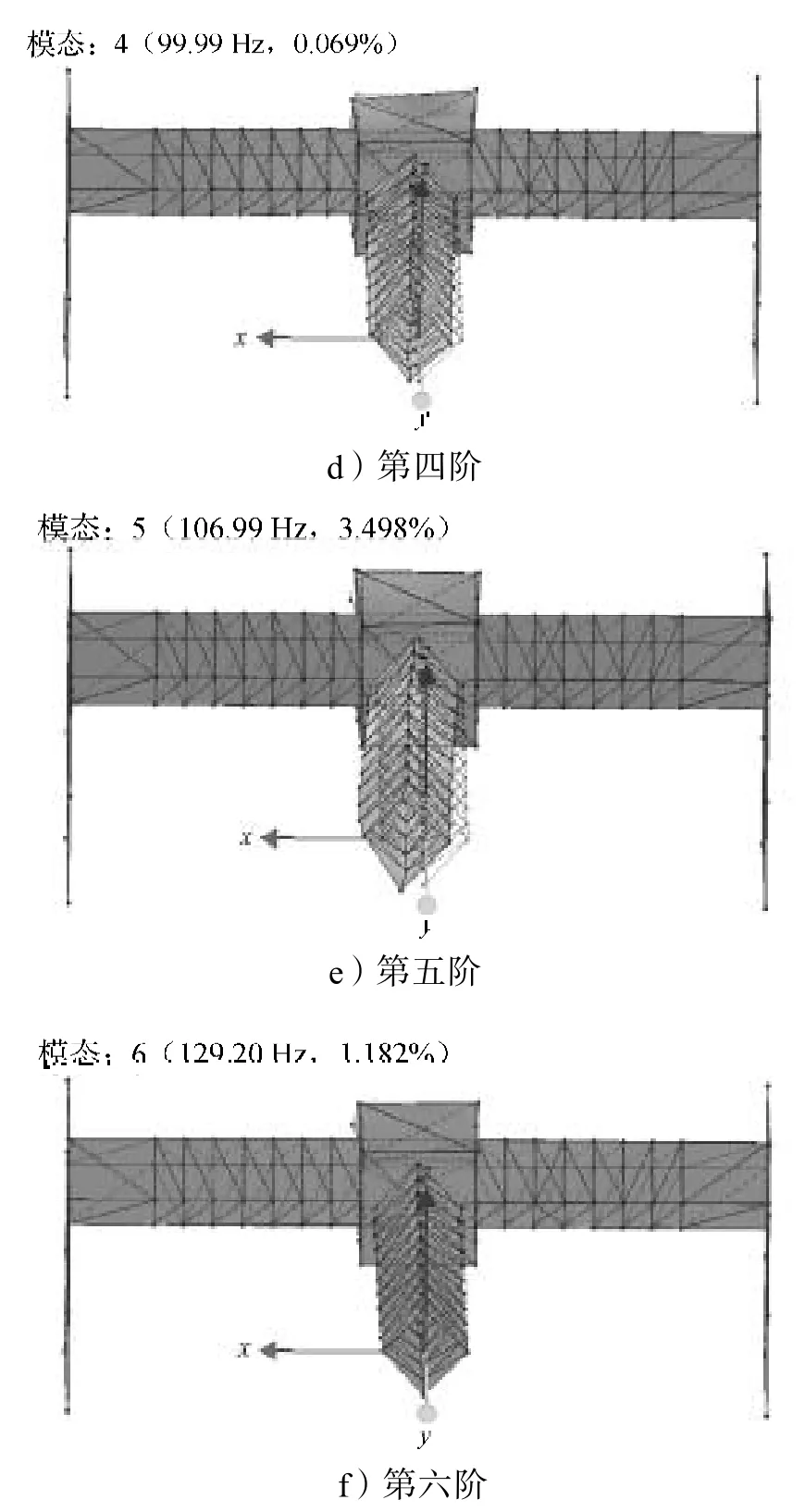
图6　机床试验模态振型Fig. 6　Mode shapes of machine tool experiments

由图6可知，前3阶模态振型的位移幅值较大，悬臂梁系统属于薄弱环节，但仍无法确定模态的主要影响因素和其振动来源。因此，需要对水射流机床进行振动测试，分析影响前3阶模态的的主要因素，找出共振频率。

2　机床振动测试

2.1振动测试

机床在切割中厚板过程中，引起机床振动的原因较多，对于五轴联动的水射流机床而言，切割头的加减速运动、水射流阀门的启闭、高压管路中水流的波动、水槽中水的波动、水槽中承料板的晃动等都可能引起机床的振动，导致加工零件的加工面被破坏。一般而言，虽然诸多因素会引起机床的振动，但在切割过程中，部分影响因素完全可以避免，如由于高压泵中有储能器，高压管路中水流的波动不会引起振动；当水槽的刚度足够时，水槽中水的波动引起的振动也可忽略；当夹紧力够大时，水槽中承料板的晃动不会引起振动。通过上述分析，本文只考虑由切割头的加减速运动所引起的机床振动，该振动产生的主要原因是机床本身的惯性作用和射流反冲击作用。

为验证上述分析，本次试验根据指定的运动轨迹，分别测试了x， y轴联动的机床空走状态下及射流工作状态下机床的振动。虽然本试验选用的机床是五轴联动机床，但水射流机床切割的零件主要为板件，轴一般不需要联动，因此，本文没有考虑 轴联动。机床切割的工作状态图如图7所示。

图7　机床切割工作状态图Fig. 7　State diagram of working cutting machines

机床空走状态下振动激励的频谱函数如图8所示。由图8可知，机床的主要共振频率分别为15.62，23.13， 31.25， 50.00， 65.63 Hz，且在23.13， 31.25 Hz处振幅最大为0.000 5G。由此可知空走状态下，x轴和y轴电机的振动及机床自身运动的自激振动是机床振动的主要来源。

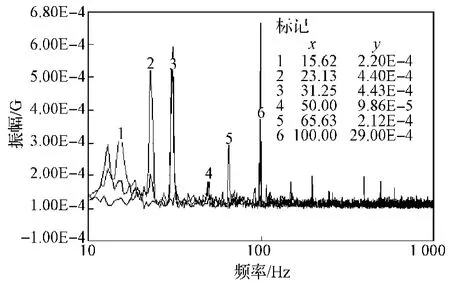
图8　机床空走状态下的频谱函数Fig. 8　Frequency spectrum function of machine tools under the state of idling

射流工作状态下振动激励的频谱函数如图9所示。由图9可知，机床的主要低阶共振频率为23.13，35.00， 58.12， 70.00 Hz，且在58.12 Hz处振幅最大为0.15G。可知相对于空走状态，机床工作状态下机床振动非常剧烈且复杂，除受x， y轴联动产生的振动外，还受到高速射流切割产生的冲击作用的影响，且振幅最大处对应模态测试第三阶固有频率，表现为悬臂梁z 轴负向摆动。

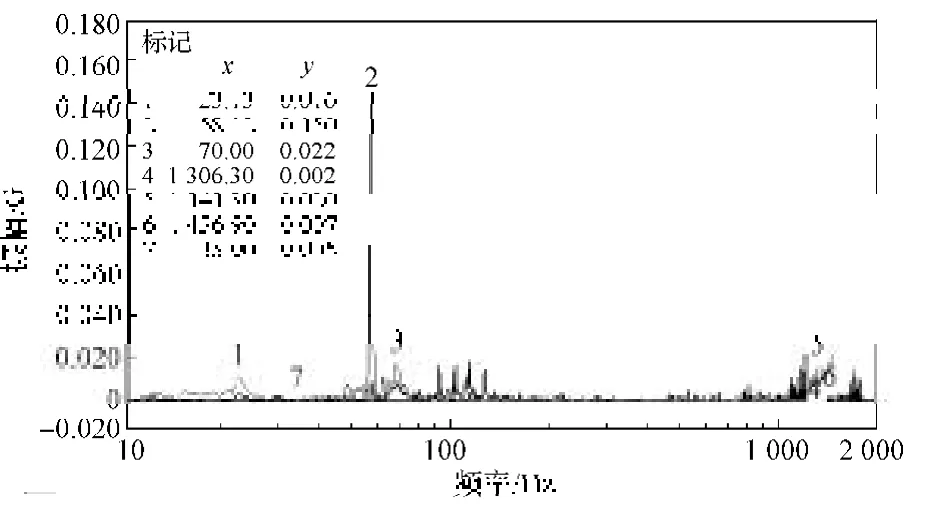
图9　机床射流工作状态下的频谱函数Fig. 9　Frequency spectrum function of working jet machines

2.2振动分析与改进措施

结合图6试验模态振型及图8，9频谱函数数据分析可知，机床振动主要集中在第一、二、三阶。第一、二阶振动来源于机床x， y轴电机的振动及其自激振动，主要表现为悬臂梁x向摆动，且在23.13， 31.25 Hz处振动最为剧烈；第三阶振动主要来源于射流反冲击作用，表现为悬臂梁 向摆动，且在58.12 Hz处振动最大。

针对上述振动现象，本文提出以下改进措施：1）机床瞬间加减速的惯性作用是自激振动产生的来源，因此，在加减速时，应尽量避开主要共振频率，并且选用电机的共振频率与第一、二、三阶固有频率尽量避开；2）为减小射流反冲击作用产生的振动，可以根据不同切割材料，使用不同压力的射流，尽可能降低射流多余能量对机床的冲击作用。

3　结语

本文采用力锤激励法对LTJ1613-5B型五轴联动智能水刀进行单点激励结构模态测试，获得机床整机的动力学特征参数（固有频率、阻尼比、模态振型），以此表征被测机床的固有属性，并通过MAC验证本次试验的正确性。通过振动响应试验可知，机床的共振主要来源于本身的自激振动及高速射流切割时产生的反冲击作用。最后，本文提出了合理的措施来避开共振频率点，以有效地降低振动，达到提高机床整机动态特性的目的。

［1］廖伯瑜，周新民，尹志宏. 现代机械动力学及其工程应用［M］. 北京：机械工业出版社，2004：3-7. LIAO Boyu，ZHOU Xinmin，YIN Zhihong. Modern Mechanical Dynamics and Its Engineering Application［M］. Beijing：China Machine Press，2004：3-7.

［2］韩清凯，于涛，孙伟. 机械振动系统的现代动态设计与分析［M］. 北京：科学出版社，2010：76-81. HAN Qingkai，YU Tao，SUN Wei. Modern Dynamic Design and Analysis of Mechanical Vibration Systems［M］. Beijing：Science Press，2010：76-81.

［3］曹文平，杨庆东. 五轴联动铣床的实验模态分析［J］. 机械制造与自动化，2008，37（1） ：71-73. CAO Wenping，YANG Qingdong. The Experimental Ental Modal Analysis of Five-Axis Milling Machine［J］. Machine Building & Automation，2008，37（1） ：71-73.

［4］葛双好，张蔚波，王佩凤，等. 基于模态实验的机床进给系统的分析［J］. 机床与液压，2015，43（1） ：37-40. GE Shuanghao，ZHANG Weibo，WANG Peifeng，et al. Analysis of Machine Tool Feed System Based on Modal Experiment［J］. Machine Tool & Hydraulics，2015，43（1） ：37-40.

［5］禇志刚 ，夏金凤. 机床整机试验模态分析［J］. 机械设计与研究，2014，30（6） ：106-108. CHU Zhigang，XIA Jinfeng. Experimental Modal Analysis of Machine［J］. Machine Design and Research，2014，30（6） ：106-108.

［6］魏要强，李斌，毛新勇，等. 数控机床运行激励实验模态分析［J］. 华中科技大学学报（自然科学版），2011，39（6） ：79-82. WEI Yaoqiang，LI Bin，MAO Xinyong，et al. Movement Exciting-Based Experimental Modal Analysis of NC Machine Tools［J］. Journal Huazhong University of Science and Technology（Natural Science Edition），2011，39（6） ：79-82.

［7］傅志芳，华宏星. 模态分析理论与应用［M］. 上海：上海交通大学出版社，2000 ：135-138. FU Zhifang，HUA Hongxing. Modal Analysis Theory and Its Application［M］. Shanghai：Shanghai Jiao Tong University Press，2000：135-138.

［8］周莉，李爱平，古志勇，等. 基于实验模态分析的机床动态性能测试［J］. 中国工程机械学报，2014，12（4） ：360-363. ZHOU Li，LI Aiping，GU Zhiyong，et al. Dynamic Performance Testing on Machine Tools Based on Experimental Modal Analysis［J］. Chinese Journal of Construction Machinery，2014，12（4） ：360-363.

（责任编辑：邓彬）

Research on Dynamic Characteristics of Five-Axis Water-Jet Machine Based on EMA

YU Xiwei，ZHANG Shijin，ZHANG Xiang，ZENG Lingliang，ZHANG Weicheng
（School of Mechatronic Engineering and Automation，Shanghai University，Shanghai 200072，China）

Based on experimental modal analysis theory， with the method of force-hammer excitation adopted， a single-input-single-output （SISO） structural modal experiment has been conducted on five-axis linkage water-jet whole machines. Combined with the response signal， an experimental modal analysis system has been established， thus acquiring the low-order inherent frequency， the damping ratio and the mode shapes of the whole machine structure， which are to be verified by the modal assurance criterion. A vibration test analysis shows that the first， second and third vibration modes are the main vibration patterns， with its vibration source to be successfully located and some corresponding measures to be taken so as to achieve the purpose of reducing vibration.

experimental modal analysis ；dynamic characteristics ；vibration test of machine tools ；modal assurance criterion（MAC）

TG664

A

1673-9833（2016）03-0019-05

10.3969/j.issn.1673-9833.2016.03.004

2016-04-06

上海张江国家自主创新示范区专项发展资金重点基金资助项目（201411-JD-C104-010）

余西伟（1990-），男，河南商丘人，上海大学硕士生，主要研究方向为机械动力学与有限元仿真分析，E-mail：jesseyxw@sina.com