助行器起坐系统优化模型研究

张　霞，孔玲爽

（1. 长沙职业技术学院 汽车工程系，湖南 长沙 410217；2. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

助行器起坐系统优化模型研究

张霞1，孔玲爽2

（1. 长沙职业技术学院 汽车工程系，湖南 长沙 410217；2. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

以患者的舒适度和系统运行效率为优化目标，对起坐系统进行了优化设计。先介绍了助行器起坐系统的原理和结构，分析了其主要元器件的数学模型，基于变分法构建了助行器起坐系统的优化模型。运用MATLAB建立了系统仿真模型，仿真结果表明：该优化模型是有效的。

起坐系统；优化模型；电控系统；变分法

对于具有协助患者进行康复训练功能的助行器，不仅能够协助患者行走，还能协助患者独立进行康复训练和调整坐姿与卧姿，提高患者生活自理能力。助行器上不同的操控系统可以实现不同的功能。起坐系统的主要功能是协助患者调整坐姿和卧姿，即根据患者的操作意图，控制相应的操控机构动作，使患者保持理想的姿势［1-3］。因此，本文对起坐系统进行研究，以患者的舒适度和系统运行效率为优化目标，根据变分法建立了起坐系统的优化控制模型。仿真结果表明，本文改进的起坐系统在调整坐姿和卧姿时，使患者感觉更加平稳、舒适。

1　起坐系统工作原理

起坐系统主要由电控系统和执行机构组成，如图1所示。电控系统主要包括电控单元、电动机、转速传感器、患者指令传感器、负荷传感器等；执行机构主要包括主动齿轮、被动齿轮、靠背机构等。

起坐系统的工作流程是：患者通过操作手柄和按钮向起坐系统发送操作指令；电控单元根据患者的操作指令、电机转速和患者质量等计算出所需的推动力和转速；再根据推动力和转速，计算电机的控制量即控制电压；通过控制电压使电机作旋转运动，从而驱动与电机刚性连接的主动齿轮也做旋转转动，再使从动齿轮做旋转运动，最后驱动靠背做相同转速和方向的旋转运动。

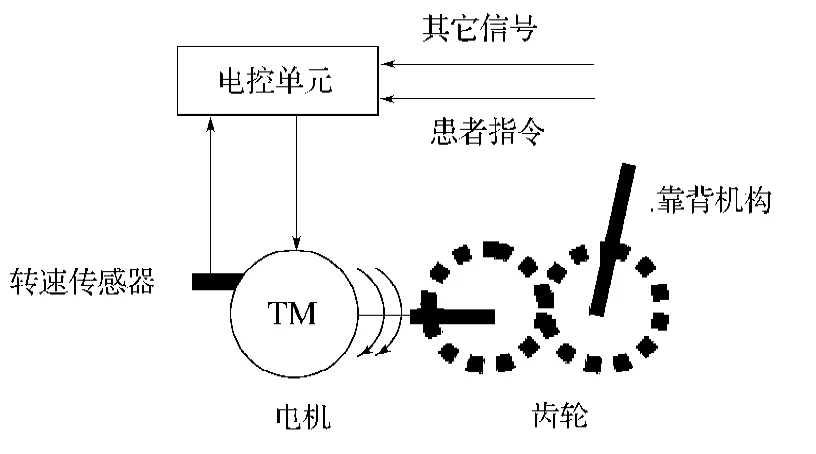
图1　起坐系统的原理简图Fig. 1　Schematic diagram of working principles for the auto-lifting system

2　起坐系统优化设计

起坐系统的性能好坏，取决于其驱动方式和控制系统的性能。1）由于直流力矩电机具有动态响应迅速，速度和位置的精度高，伺服刚度高，特性的线性度好，结构紧凑，运行可靠，维护方便，震动小，机械噪声小，控制简单等优点，驱动方式采用直流力矩电机［4-6］。2）当患者从卧姿转换到坐姿时，发送起坐指令到电控单元，电控单元控制整个系统执行动作，推动靠背从水平位置旋转到与水平位置成一定角度的倾斜位置，使患者从卧姿转换到坐姿。因此，考虑到患者的舒适度，执行动作的安全性，以及系统的运行效率，主从动齿轮的角加速度和转速需要进行优化控制。

2. 1电机数学模型

直流力矩电机的电枢电路原理图［7］如图2所示。

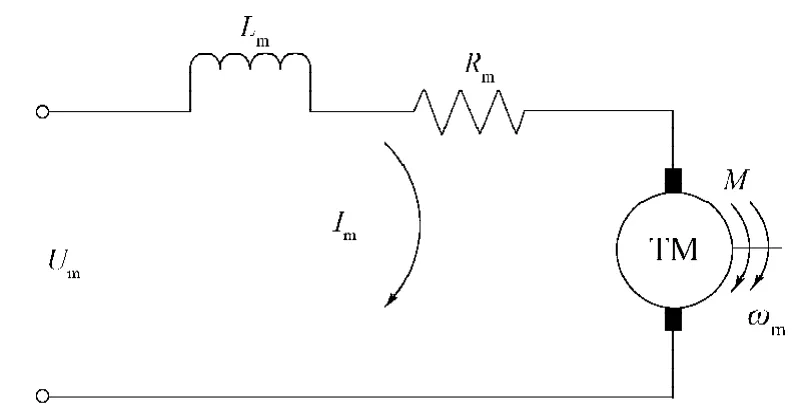
图2　直流电机电枢电路原理Fig. 2　Circuit schematic diagram for DC motor armatures

图2中， Um为电机的输入电压，Rm为电枢电阻，Lm为电枢电感，Im为通过电枢的电流，m为电机转速，M为电磁力矩。

由基尔霍夫电压定律得

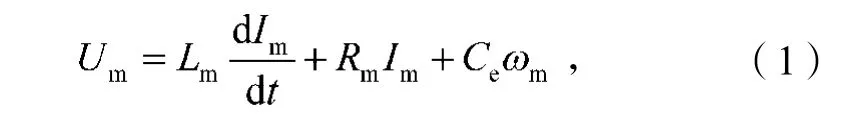
式中Ce为电动势常数。

由动力学方程得

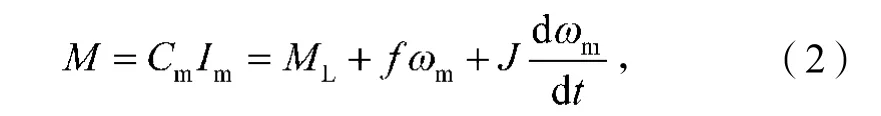
式中：Cm为转矩常数；

f为集中黏性摩擦系数；

ML为负载力矩；

J为电机的转动惯量。

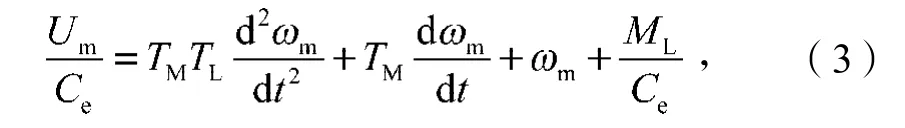
式中：TM为电机的机电时间常数，；

TL为电机的电磁时间常数，。

设电机侧的主动齿轮与从动齿轮的传动比为i，两齿轮的啮合处线速度相等，角速度为i倍关系。由式（3）可知，电控单元的输出控制电压Um决定齿轮的运动速度m。

2. 2优化模型

以患者发出控制指令从卧姿转换到坐姿为例，该转换过程分为3个阶段：加速阶段、匀速阶段、减速阶段，如图3所示。1）加速阶段即0～tc时刻，齿轮以一定的加速度从零转速加速到预定的转速；2）匀速阶段即tc～td时刻，齿轮按照预定的转速做匀速运动；3）减速阶段即td至结束时刻，当靠背快要到达坐姿位置时，齿轮开始做减速运动，以一定的加速度减速到0 rad/s，即当靠背到达预定位置时，齿轮停止运动，转速为0 rad/s。由图可知，加速阶段tc时刻的速度是匀速阶段的速度，也是减速阶段的初始速度；加速阶段与减速阶段的加速度绝对值是按时间对称的。

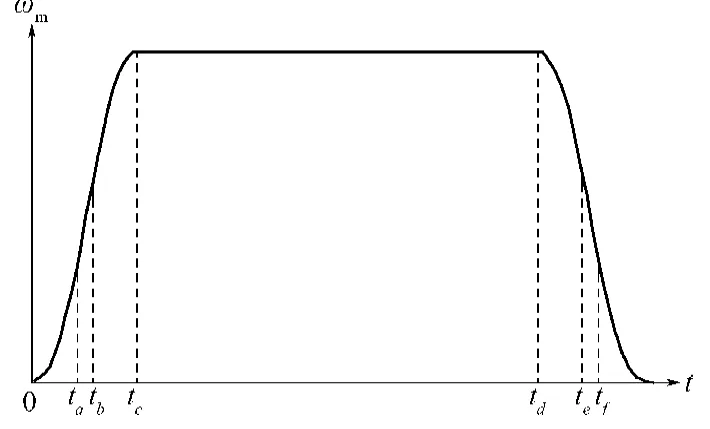
图3　速度-时间曲线Fig. 3　A curve graph for velocity-time parameters

对于患者来说，上述转换过程要平稳可靠，即舒适度高；转换时间越短越好，即系统的运行效率高。因此，本文将患者的舒适度和系统的运行效率作为起坐系统的优化目标［8］。而患者的舒适度和系统的运行效率主要体现在加速阶段和减速阶段，因此，本文优化了加速阶段，而减速阶段采用对称的方法即可。

患者的舒适度主要取决于加速阶段和减速阶段的加速度和加速度变化率，即与齿轮的角加速度 和加速度变化率d/dt有关。齿轮的角加速度和加速度变化率越小，舒适度越好；反之，舒适度越差。因此，要提高患者的舒适度，就要使齿轮在加减阶段齿轮的角加速度和加速度变化率尽量的小。

系统的运行效率主要取决于电机转速m和齿轮的角加速度 。m和 越大，系统的运行效率越高。因此，要提高系统的运行效率即缩短转换时间，就要提高和 ，其中。

以加速阶段为例，本文将其分为3个时间段（见图3）。每个时间段的加速度运行方式不一样。

1）0～ta时刻，齿轮的角加速度逐渐增加。0时刻，角加速度为0 rad/s2。ta时刻，角加速度为整个过程的最大角加速度。

2）ta～tb时刻，齿轮为匀加速运动，角加速度为。

3）tb～tc时刻，齿轮的角加速度逐渐减小。tc时刻，角加速度为0 rad/s2，电机转速为最大值。

0～ta时刻与tb～tc时刻两个阶段的运行时间相等，且按时间对称，对应加速度的绝对值相等。

由以上分析可知，如要提高舒适度，则要减小角加速度和角加速度的变化率；如要提高系统的运行效率，则要缩短运行时间，增加角加速度和角速度。这两个目标不能同时最优。因此，本文给患者舒适度和系统的运行效率这两个目标赋予了相应的权重系数，使两个目标的优化问题转化为单目标优化问题（见式（4）），即优化目标函数J′的值为最小。

整个转换过程，影响患者的舒适度的主要因素是加速度的变化率。为了简化问题，在舒适度指标中，只把角加速度的变化率引入优化目标函数中；而角加速度的大小作为优化目标函数的边界条件，该角加速度为整个转换过程中的最大角加速度和平均角加速度，其中最大角加速度反映极端的舒适度，而平均角加速度反映整体的舒适度。

优化目标函数即电机的转动惯量为

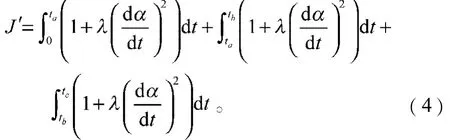
式中：ta= tc- tb；为加权系数。

设加速阶段的平均角加速度为av，即

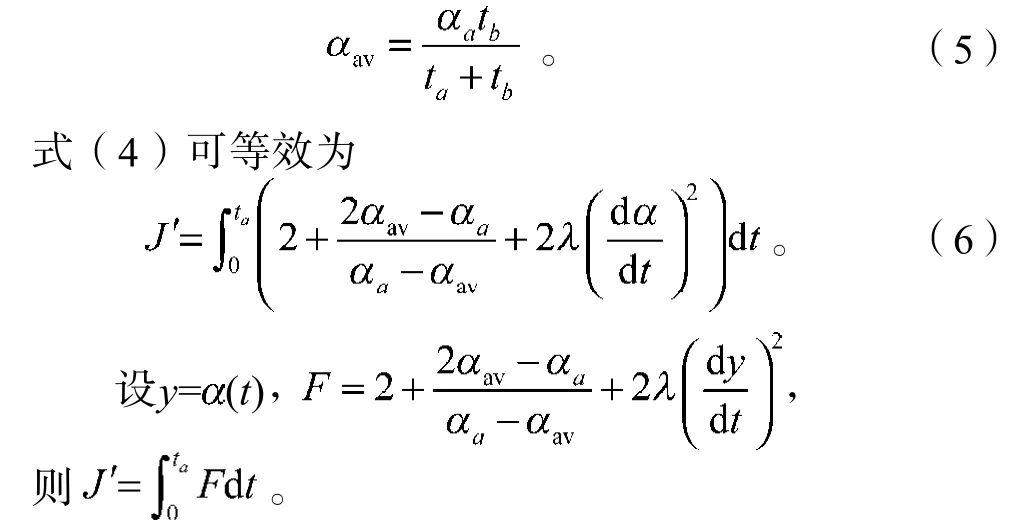
使加速阶段的优化目标函数J′值达到最小，为经典变分法中的固定边界变分问题［9］，即确定函数y=（t）。函数J′取极值的必要条件是满足欧拉方程；函数J′取极小值的充分条件是函数J′使魏尔斯特拉斯极值条件成立。因此，本问题先求解欧拉方程，再根据边界条件求解（t），最后判断魏尔斯特拉斯极值条件是否成立。

式中c1， c2为系数。

将边界条件代入式（7）中，t=0时，y=0 ；t= ta时，，得

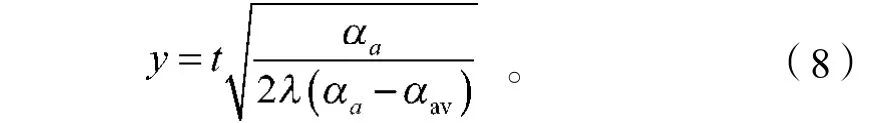
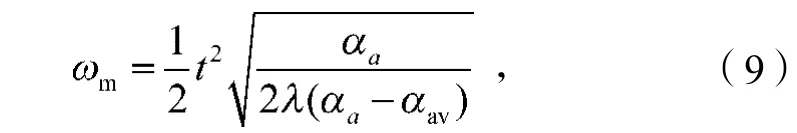
代入式（3）中，得

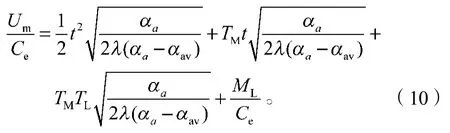
从动齿轮的转矩随着靠背转角的改变而改变，即电机的负载力矩ML随着靠背转角的改变而改变。当靠背转角为0°时，负载力矩ML最大；当靠背转角为90°时，负载力矩ML最小。由式（9）可得靠背转角m，即

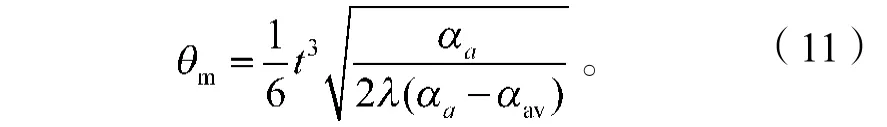
由式（11）可得负载力矩ML，即

式中k为患者质量与靠背长度相关的系数。

由式（10）和式（12）可得

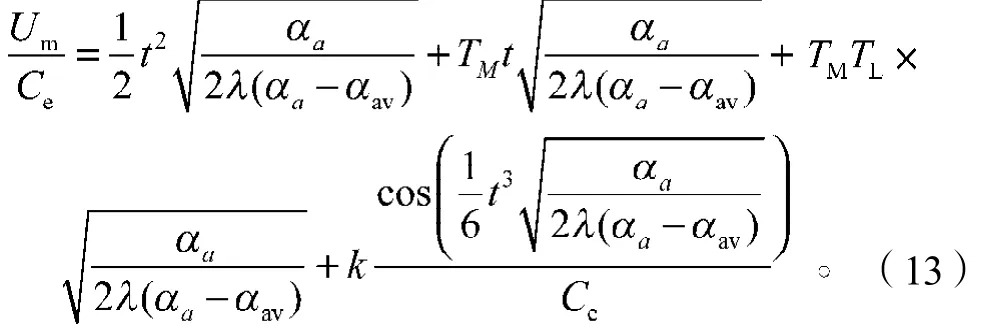
式（13）是起坐系统的优化模型函数表达式。该式表明了电控单元输出的控制电压与时间的关系。

3　仿真试验

本文运用MATLAB软件仿真分析了助行器的起坐系统。仿真参数［10］设置如下：TM=2.86 ms，TL=0.443 ms，

3.1控制电压仿真分析

根据式（13），得到加速阶段的输出控制电压曲线，如图4所示。

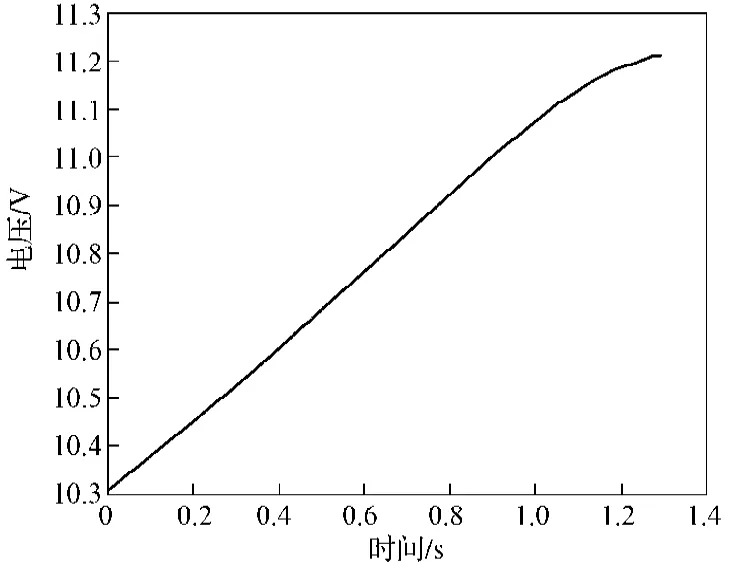
图4　控制电压曲线Fig. 4　A curve graph for control voltage

从图4可以看出，当t＜1.15 s时，输出控制电压与时间的关系接近线性关系；t＞1.15 s时，其线性关系不明显。

3.2电机角加速度仿真分析

根据式（8），得到加速阶段的电机角加速度曲线，如图5所示。

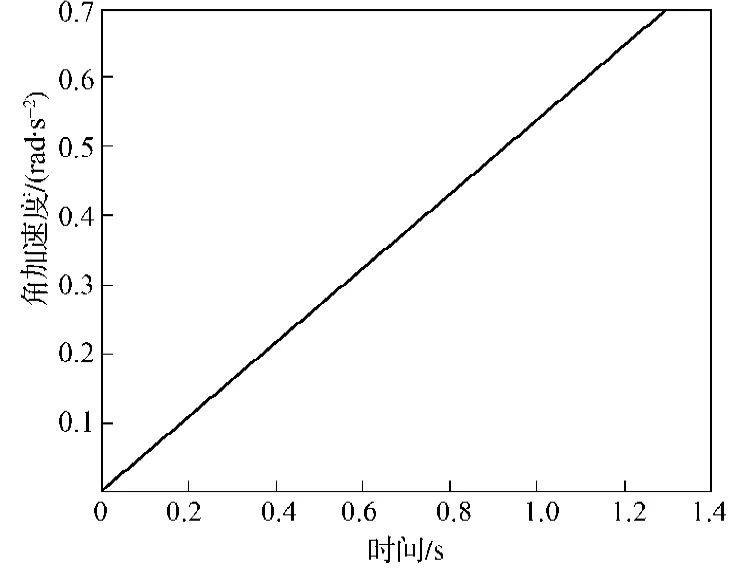
图5　角加速度曲线Fig. 5　A curve graph for the angular acceleration

从图5可以看出，角加速度曲线是一条斜率固定的直线。改变舒适度的加权系数可得到不同斜率的直线。如果要求舒适度更好，则增大加权系数，减小斜率；如果要求效率更高，则减小加权系数，增大斜率。

3.3电机角速度仿真分析

根据式（9），得到加速阶段的电机角速度曲线，如图6所示。

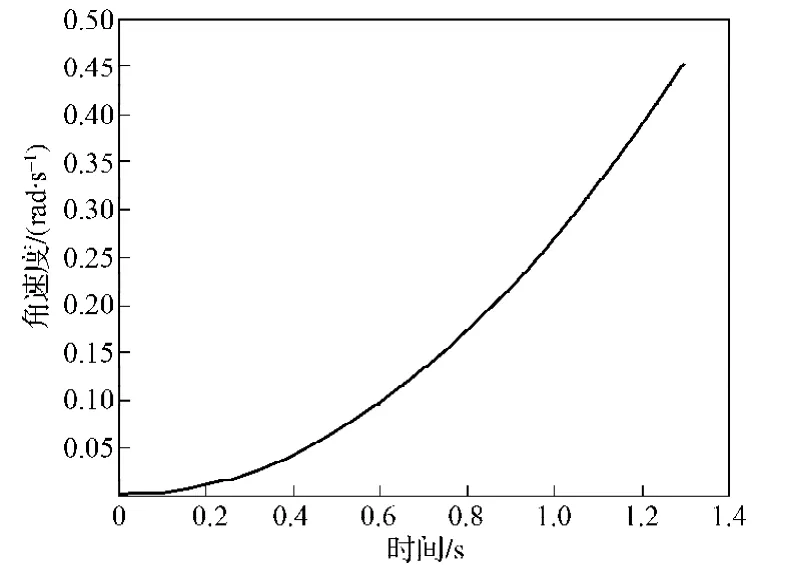
图6　角速度曲线Fig. 6　Angular velocity curve

从图6可以看出，角速度曲线是一抛物线。改变舒适度的加权系数可得到不同抛物线。如果要求舒适度更好，则增大加权系数，使抛物线更平坦，速度变化减小，让人觉得舒服；如果要求效率更高，则减小加权系数，使抛物线更陡。

3.4电机角位移仿真分析

根据式（11），得到加速阶段的电机角位移曲线，如图7所示。

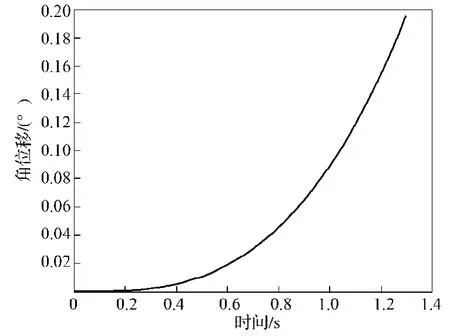
图7　角位移曲线Fig. 7　A curve graph for the angular displacement

从图7可以看出，角位移的最大值不到0.2°。如要使起坐系统运行更平稳，则在加速阶段角位移应尽量小，即缩短加速阶段的时间；如要使系统运行效率更高，则在加速阶段角位移应尽量大。在模型参数当中，最大角加速度和平均角加速度对加速阶段角位移影响较大，这两者的值越大，加速阶段角位移越大；反之越小。

4　结语

助行器可以协助患者进行康复训练。本文对助行器的起坐系统进行了优化设计，基于变分法建立了起坐系统的优化模型，并运用MATLAB软件对该模型进行仿真分析，仿真结果表明，该模型是有效的。在实际应用中，可修改模型的某些参数，使起坐系统能更好地满足患者的需求。

［1］白大鹏. 多功能助行机器人机构研究［D］. 哈尔滨：哈尔滨工程大学，2013. BAI Dapeng. Research on Mechanism of Multifunctional Walking Assistance Robot［D］. Harbin ：Harbin Engineering University，2013.

［2］邱若琳，张秋菊，邱玉宇. 老年人助步需求调查与分析［J］.甘肃医药，2014，33（9） ：648-651. QIU Ruolin，ZHANG Qiuju，QIU Yuyu. The Analysis of the Elderly's Stepping Demands and the Situation of Walking Aids［J］. Gansu Medical Journal，2014，33（9） ：648-651.

［3］张峻霞，尹由之，温泉，等. 人体下肢动力助行器的结构设计与仿真［J］. 机械设计，2015，32（9） ：71-75. ZHANG Junxia，YIN Youzhi，WEN Quan，et al. Structure Design and Simulation of Dynamic Walking-Aid［J］. Journal of Machine Design，2015，32（9） ：71-75.

［4］于宝成，龙冲，王春梅. 基于直流力矩电机的位置控制伺服系统研究［J］. 武汉工程大学学报，2015，37（10） ：40-44. YU Baocheng，LONG Chong，WANG Chunmei. Servo System of Stable Speed Control Based on Direct Current Torque Motor［J］.Journal of Wuhan Institute of Technology，2015，37（10） ：40-44.

［5］李宝荣，李先峰，颜昌翔，等. 基于System Generator直流力矩电机模型及控制系统仿真［J］. 仪表技术与传感器，2013（3） ：105-107. LI Baorong，LI Xianfeng，YAN Changxiang，et al. Simulation of DC Torque Motor Model and Control System Based on System Generator［J］. Instrument Technique and Sensor，2013（3） ：105-107.

［6］雷杨，李军，李绍军，等. 高精度稳定平台伺服控制系统仿真实现［J］. 电光与控制，2015，22（5） ：72-76. LEI Yang，LI Jun，LI Shaojun，et al. Simulation Realization of High Precision Stabilized Platform Servo Control System［J］. Electronics Optics & Control，2015，22（5） ：72-76.

［7］梅晓榕. 自动控制元件及线路［M］.北京：科学出版社，2010：10-234. MEI Xiaorong. Automatic Control Elements and Circuits［M］. Beijing：Science Press，2010 ：10-234.

［8］袁艳丽，关天民，秦美超. 轮椅舒适度评价体系与评价方法研究［J］. 机械科学与技术，2014，33（3） ：332-338. YUAN Yanli，GUAN Tianmin，QIN Meichao. Study on System and Method of Wheelchair Comfort Evaluation［J］. Mechanical Science and Technology for Aerospace Engineering，2014，33（3） ：332-338.

［9］老大中. 变分法基础［M］. 北京：国防工业出版社，2015：98 -120. LAO Dazhong. National Defense Industry Press［M］. Beijing：National Defence Industry Press，2015 ：98-120.

［10］刘金琨. 先进PID控制MATLAB仿真［M］. 3版. 北京：电子工业出版社，2011：10-68. LIU Jinkun. Advanced PID Control MATLAB Simulation［M］. 3rd ed. Beijing：Electronic Industry Press，2011：10-68.

（责任编辑 ：邓彬）

Research on Optimized Models for the Auto-Lifting System of Walking Aids

ZHANG Xia1，KONG Lingshuang2
（1. Department of Automotive Engineering，Changsha Vocational and Technical College，Changsha 410217，China；2. School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

An optimized design has been proposed for the auto-lifting system of walking aids， with its comfortableness and operating efficiency the optimization objectives. An introduction has been made of the working principle and structure of the auto-lifting system of walking aids， followed by an analysis of the mathematical model of its main components. And then an optimized modeling， based on the variation method， has been proposed for the auto-lifting system of walking aids，with a simulation model based on MATLAB thus established for the system. The simulation result shows that the optimized model is effective for practical applications.

auto-lifting system ；optimization model ；electric control system ；variation methods

TP272

A

1673-9833（2016）03-0077-05

10.3969/j.issn.1673-9833.2016.03.014

2016-03-16

湖南省高校科学研究基金资助项目（14C0133）

张霞（1972-），男，湖南澧县人，长沙职业技术学院副教授，主要从事汽车安全技术方面的研究，E-mail：zx7206@126.com

孔玲爽（1979-），女，河北邢台人，湖南工业大学副教授，博士，主要从事复杂工业过程建模与优化控制方面的研究， E-mail：konglingsh@126.com