基于多尺度重采样思想的类指数核函数构造
2016-10-14胡站伟焦立国徐胜金
胡站伟 焦立国 徐胜金 黄 勇
基于多尺度重采样思想的类指数核函数构造
胡站伟①②焦立国③徐胜金*①黄 勇②
①(清华大学航空航天学院流体力学所 北京 100084),②(中国空气动力研究与发展中心 绵阳 621000),③(大庆地区防洪工程管理处 大庆 163311)
该文按照多尺度重采样思想,构造了一种类指数分布的核函数(ELK),并在核回归分析和支持向量机分类中进行了应用,发现ELK对局部特征具有捕捉优势。ELK分布仅由分析尺度决定,是单参数核函数。利用ELK对阶跃信号和多普勒信号进行Nadaraya-Watson回归分析,结果显示ELK降噪和阶跃捕捉效果均优于常规Gauss核,整体效果接近或优于局部加权回归散点平滑法(LOWESS)。多个UCI数据集的SVM分析显示,ELK与径向基函数(RBF)分类效果相当,但比RBF具有更强的局域性,因此具有更细致的分类超平面,同时分类不理想时可能产生更多的支持向量。对比而言,ELK对调节参数敏感性低,这一性质有助于减少参数优选的计算量。单参数的ELK对局域特征的良好捕捉能力,有助于这类核函数在相关领域得到推广。
多尺度重采样;Nadaraya-Watson回归;支持向量机;类指数核函数
1 引言
核方法(kernel method)自二十世纪90年代引入模式识别与机器学习后,取得了巨大的成功,在信号回归、特征识别、聚类分析、运动检测等非参数机器学习领域有广泛的应用,其中支持向量机(Support Vector Machine, SVM)的发展尤为迅速。核方法的研究主要集中在两方面:(1)核方法与常规的线性学习方法的结合,如基于核函数的主成分分析(KPCA)[5];(2)核方法中核函数的构造与核参数的优选。本文对(2)进行研究。
核函数的构造通常有3种途径[6,7]:改造常用分布函数、构造核函数、组合核函数。一些应用通过构造核矩阵来代替一个显式的核函数,来实现对具体问题核参数调整的要求[8]。常见核函数大多基于线性、多项式、高斯分布、样条函数等分布,通过改造使其性质满足Mercer定理要求。构造核函数针对字符、图像、生物信息等特殊应用,以实现对信息的高效提取。组合核函数原则上可实现核函数程序化优化,组合形式包括不同适用范围核函数的组合、不同局域性的核函数组合、不同尺度的同一核函数的多分辨组合等形式[9]。
多分辨组合的小波核函数,使用多尺度小波的非负线性组合,实现对某一空间上目标函数的高精度逼近[10]。借鉴这一思想,对空间上的目标函数直接进行多尺度重采样,也可以获得对目标函数的稳健估计;将这一过程使用单一核函数进行描述,可使多分辨组合核函数参数优化的计算量显著降低。
以提升信号局部信噪比为分析样本,通过对瞬态信号进行时域多尺度重采样,本文构造了一种以分析尺度为唯一参量的类指数核函数(Exponential- Like Kernel, ELK),并通过数值仿真来讨论该核函数在回归分析和SVM中的适应性。
本文首先对局部回归和SVM这两种核方法简单介绍;然后,通过引入时域多尺度重采样的概念,导出了ELK。利用ELK对两类典型非稳态信号进行了回归处理,分析了ELK的降噪和瞬态信号捕捉性能。通过对比几组UCI标准数据的SVM分类效果,讨论了ELK的参数敏感特征;最后,对ELK的应用和局限进行了讨论。
2 两种核方法的介绍
2.1 局部回归
信号回归中一项重要内容就是对瞬态信号的提取[11]。在常见的样条平滑、正交回归等方法中,大多隐含了对数据分布形式的强制拟合(使用样条函数、小波基函数等),容易引起信号畸变。局部回归是一类易于保留信号局域特征的非参数回归分析,主要包括:核回归分析、局部多项式回归分析、稳健回归分析等方法[12]。N-W(Nadaraya-Watson)回归在核回归方法中发展历史较早,形式简单、便于分析[13],其核概率密度分布加权累加形式为
常见的核函数包括:均匀核函数、高斯(Gauss)核函数、三角核函数等[12]。核回归分析的研究表明,相对于核函数的选择,更为关键的是分析带宽的选取[2,4]。
2.2 SVM
SVM是由文献[14,15]在20世纪末提出的一种基于统计学习理论的新型机器学习方法。在SVM方法中,高效和具有良好扩展性的核函数的选择,是模型复杂度和鲁棒性的关键[14,16]。方法中核参数选择算法包括:grid search 暴力搜索方法,启发式GA, PSO方法等[17]。恰当选择核函数及其参数,或者寻求对低参数敏感性的核函数以降低参数计算成本也是该类问题的研究热点[16]。
SVM常见的核函数类型有:线性、多项式、径向基函数(Radial Basis Function, RBF)和Sigmoid函数、样条核函数等。其中,RBF具有高维数映射能力和参数相对简单的特点,常被用作未知数据集处理的默认核函数。RBF的形式为
SVM算法在机器学习的几大领域:模式识别、回归估计、概率密度函数估计等都有应用。特别地用于分类的模式识别方面,对于手写数字识别、语音识别、人脸图像识别、文章分类等问题,SVM算法在精度上达到甚至优于其他传统算法。
3 方法介绍
过采样技术可以有效地增加信噪比,但在采样样本既定的情况下,充分并合理利用有限的采样点,有效减小估计偏差,是信号识别的重要内容。借鉴微弱信号识别中采用的取样积分方法的思想[21],可以对信号进行多尺度重采样,并利用多个采样样本的组合来提高信噪比。
3.1多尺度重采样
对于同一个弱的脉冲信号,相同背景噪音下多探测器同步测量,其累加结果会类似于取样积分的效果。按照这一思路,可以将一个高频采样信号(),人工分为多组较低频率的采样信号x(t),构成重采样信号组。
从采样间隔的设定方法上区分,重采样可分为定间隔的采样法dTc、间隔递增的采样法dTn两种。dTc方法与常规的降采样过程类似,对信号总长度为的原始数据,从任意一点开始,以固定的间隔选取样本点就可以获得一组单尺度重采样数据。记原始样本间隔为, dTc方法可表述为
图1展示了对含噪矩形阶跃信号,不同重采样方法的效果。原始信号总长度201,脉冲位于时间序列中部、宽度21,信噪比()设为5.6 dB。可以看到,dTc方法各样本尺度相同,在阶跃点附近失真显著。dTn不同尺度样本对阶跃特征的捕捉效果存在差异,且数据样本间的采样点数不同,在样本累加处理上需要进行样本重构。以下重点讨论dTn方法。

图 1 多尺度重采样点示意图
3.2 时域多尺度重采样构造的窗函数
多尺度重采样数据重构时,需要充分利用瞬态信号在时域上影响范围有限的特征。考虑局部长度为的一段信号进行采样,按照dTn方法共取组多尺度重采样样本,即存在个有效数据点。某一时刻多尺度重采样样本累加结果可表示为
该权函数端点值非0,关于中心对称,且自然满足归一化,如图2(a)。由于该分布的形状与指数分布相似,因此将该分布记作类指数(Exponential Like, EL)分布。EL分布在中心区具有局部极大,近似指数分布;在远端迅速衰减,更接近高斯分布。

图 2 ELK分布与高斯分布、指数分布之间的对比
以上分析中,分别提到基于dTc的采样平均(记作dTc AVG)、基于dTn的线性插值(dTn LInter)和基于dTn的原始信号填充(dTn OSP)3种方法。可以从幅值跟踪、阶跃位置逼近和降噪效果3个方面对比这几种方法的降噪处理效果。根据图3,最大采样样本尺度越窄,降噪效果越差,但对于阶跃捕捉越准确。具体而言,dTc AVG方法造成过度平滑,在幅值跟踪和边缘检测方面较差;dTn LInter方法在幅值跟踪、阶跃位置逼近方面均不理想;dTn OSP方法各指标均最佳,但随分析尺度增加,其阶跃位置也会产生模糊。
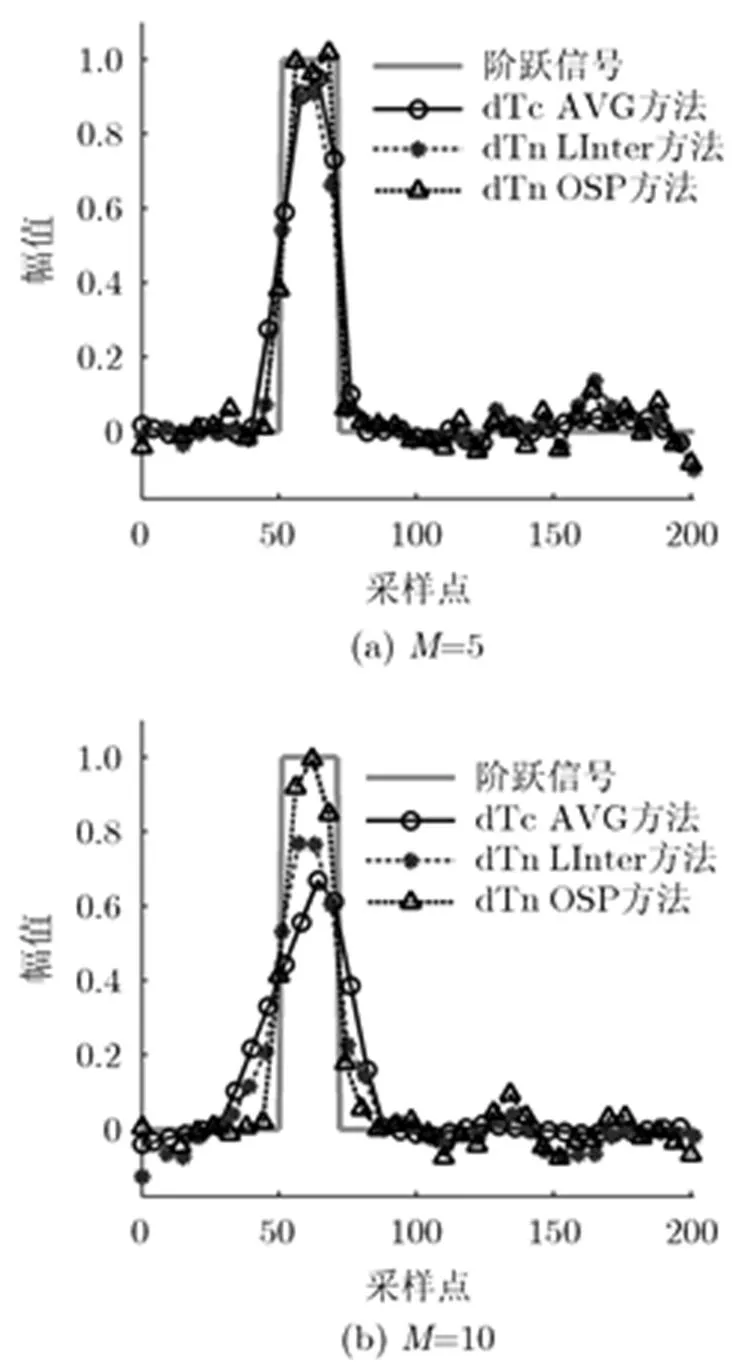
图 3 不同降噪方法的效果对比
3.3 类指数分布核函数
式(9)所示加权函数,满足式(2)的核函数条件,因此可以称之为类指数分布核函数(ELK)。 用于SVM时,不关心归一化,也可以表述为基于向量空间范数的ELK形式:
由于ELK是对称正分布,ELK的Gram矩阵是正定的。使用数值仿真可以证明,ELK对于任意两个维向量映射的核函数矩阵,都是对称半正定的。按照Mercer定理[22],ELK是一个有效核函数。从分布上看,ELK与高斯核一样,同属于径向对称核函数,计算复杂程度一致。由于ELK具有强局域性,作用于核方法时可以获得精细的局部特征。
4 类指数分布函数回归分析
对于不同的信号类型,不同核函数在最优的带宽选择下会有近似的结果,但核函数对于带宽的敏感性会有所不同。核回归分析中常用Gauss核,以下即对ELK与Gauss核在N-W回归中的效果进行对比。为增强对比的有效性,引入局部加权回归散点平滑法(LOWESS)作为参照。
模拟分析信号采用Matlab软件的Wnoise函数产生,主要讨论包括阶跃和多普勒两种典型信号。为保证对瞬态细节显示,信号的长度选择为1024点。通过改变原始信号SNR、调整核函数的带宽进行分析。模拟信号回归估计效果的评估,采用均方误差(Mean Squared Error, MSE)。考虑到N-W回归的边界效应,设计归一化MSE并不引入边界部分的影响:
此外,为了衡量算法对于阶跃量的拟合效果,构造阶跃平方误差(Step Squared Error, SSE)函数。记,阶跃平方误差仅包含强阶跃信号:
4.1 阶跃信号回归分析
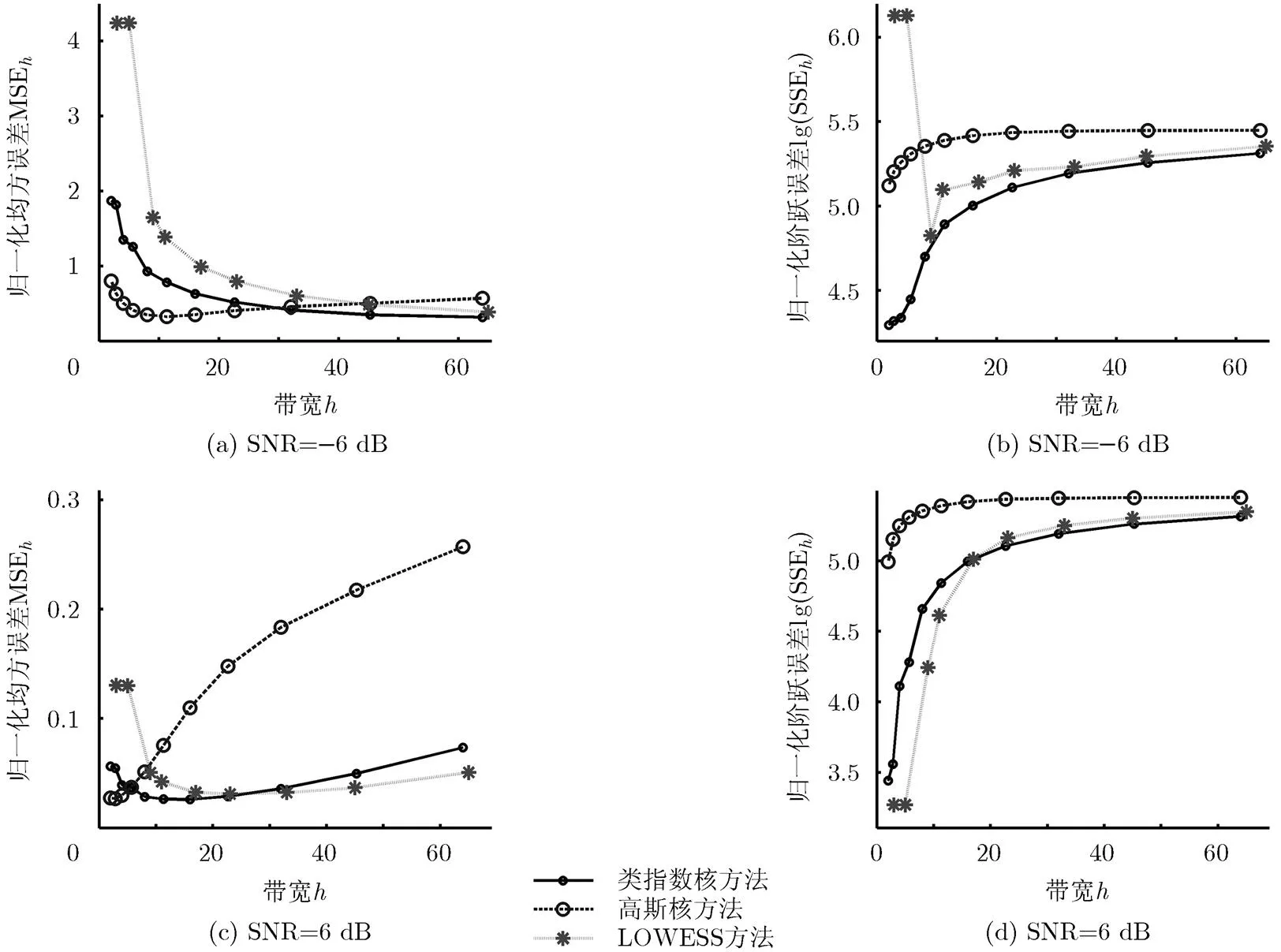
图4 含噪阶跃信号不同回归方法的参数影响对比
ELK的N-W回归结果,整体上效果优于以上两种方法。除了在局部小带宽低SNR的情况下,ELK由于具有对局部的高加权因子的性质,得到了与LOWESS方法相似的高MSE。这一现象的成因在于低SNR信号回归中,需要较大样本才能取得相对较好的回归效果,因此需要选择较大的带宽。
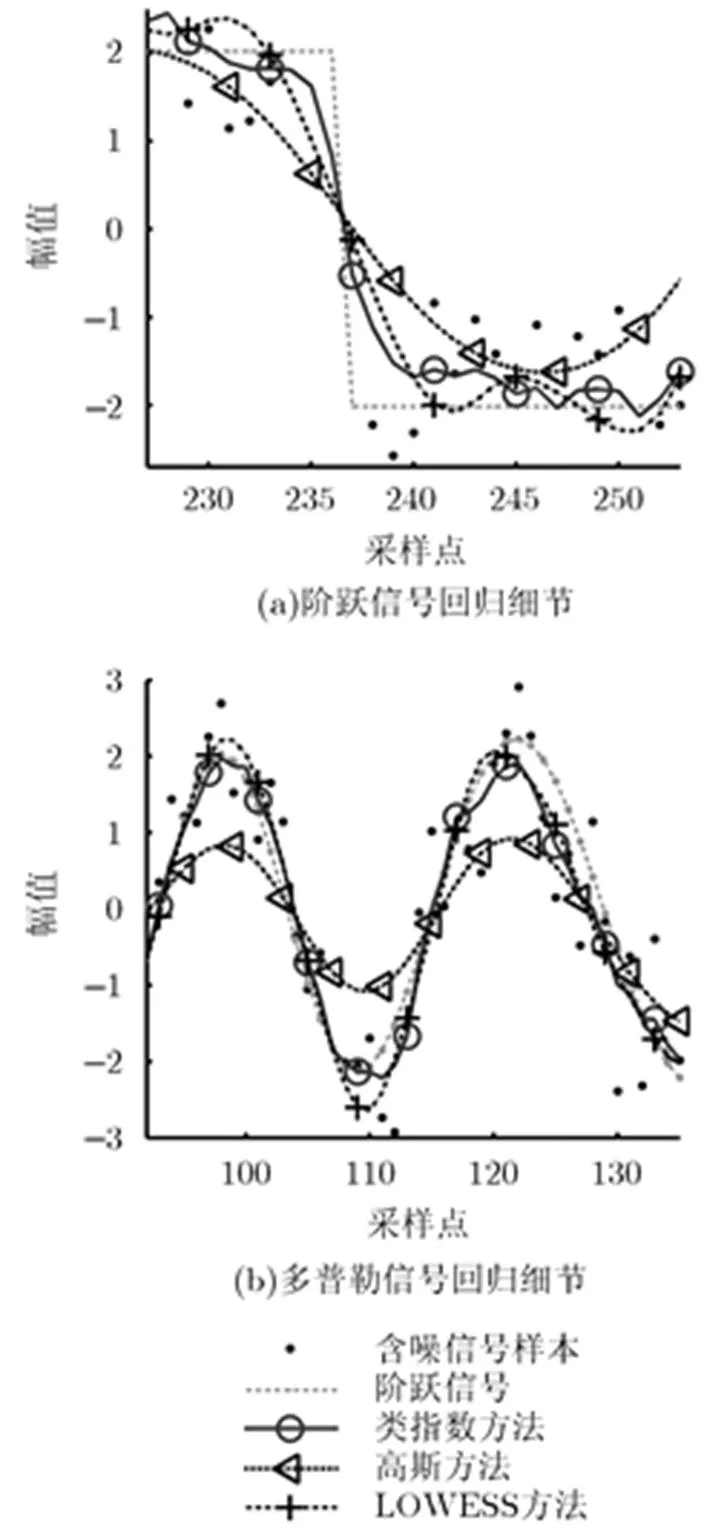
图 5 含噪阶跃信号不同回归方法的效果对比
4.2 多普勒信号回归分析
对于含噪多普勒信号,SNR和带宽对回归效果的整体影响与阶跃信号类似(图略)。同样以各算法最优带宽对含噪多普勒信号进行回归,其效果对比参见图5(b)。
5 类指数分布函数SVM性能分析
不同核函数对SVM的分类性能会有影响,同时核函数参数也对分类问题的效果影响显著[23]。在考察在分类问题中不同核函数的性质时,均选择C-SVC(C-Support Vector Classification)算法,并采用SMO求解;核函数效果检验使用多组UCI 数据集。
5.1 ELK用于SVM时的分类超平面对比
以fisheriris的部分数据为例[24],以花萼宽度和花萼长度对两类(Verg., Vers.)鸢尾花进行分类,直观考察不同核函数的分类特征。选择默认罚函数,对参数的影响进行了分析(图略)。两个核函数在各自的最优参数下最大失误率相当,参数变化范围内ELK分类效果整体上更接近最优。图6给出了最优时支持向量分布,可以看出ELK相对于RBK,对于同样的参数,其分类超平面更为细致,表明具有显著的局域性。
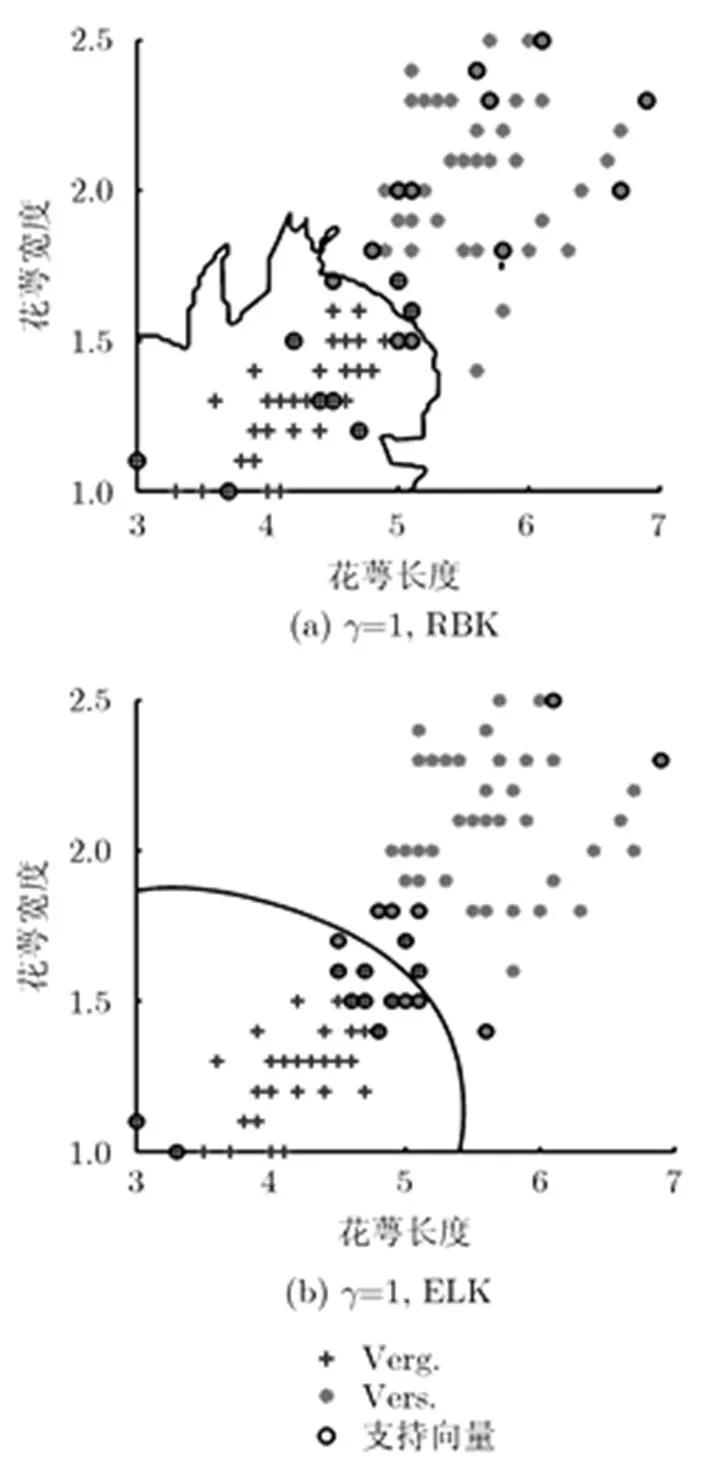
图 6 RBK与ELK用于fisheriris数据分类
5.2 ELK在SVM中的性能对比
在核函数效果的对比验证中,使用UCI数据库的fisheriris, glass, heart, wine数据集[24],进行分类效果检验。数据集的参数描述见表1。分类计算使用LibSVM工具箱。为了考察核函数的性能,罚函数和部分参数的使用网格搜索法对最优核参数进行选择,并使用5-折交叉验证正确率(5-Cross Validation Accuracy, 5-CVA)、使用支持向量数(number of Support Vector, nSVs)来估计LOO (Leave-One-Out) 误差上限等方法对最优参数下不同核函数的效果进行对比。仿真过程中,首先对各参变量进行归一化预处理,防止出现参数特征对分类效果的影响。
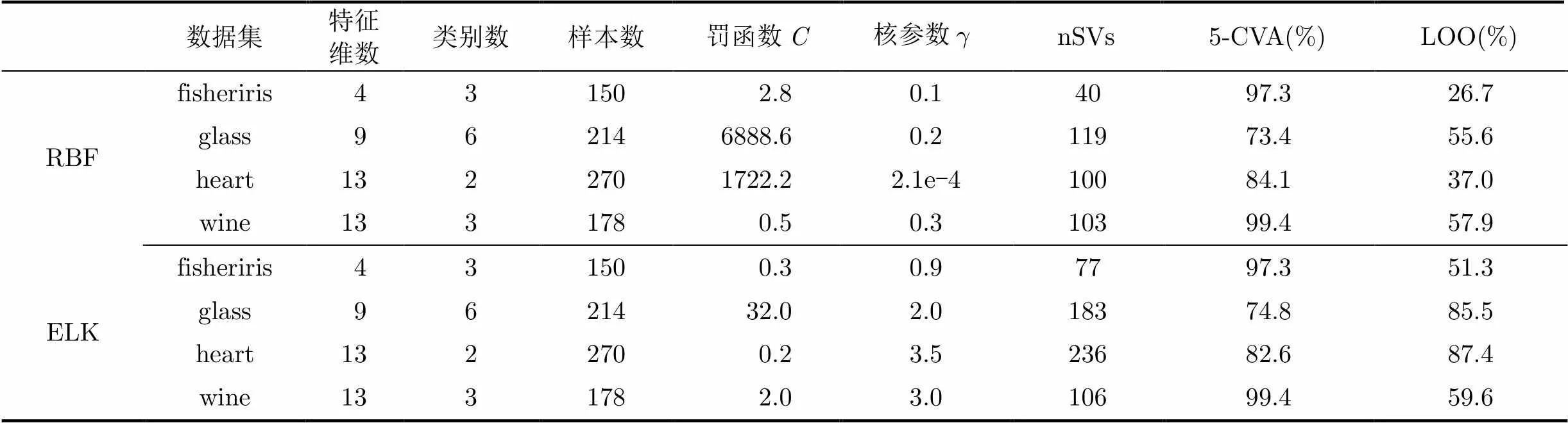
表1 各UCI数据集使用不同核函数的最优分类效果
各数据集最佳分类正确率下,不同核函数的参数值及支持向量数见表1。不同数据集下,ELK参数整体上量级更为接近,因此在参数选择上可以以较小的代价进行参数优选。从5-CVA效果看, ELK比RBF具有相当或者更优的结果。这一结果与ELK对于局部特征的显著捕捉能力有关,这一点也体现在ELK在分类效果不良时所需要的支持向量数量远大于RBF的支持向量数量。支持向量增加会引起LOO误差上限增大,也增加过拟合的风险。
图7给出了不同参数组合下两种核函数的对Iris分类准确率分布。ELK最优参数的分布区间相对集中,且在优选区域内罚函数的变化对分类准度的影响相对较小,更多的影响到支持向量的数目。这一性质有助于大大减少参数选择所需的计算量。
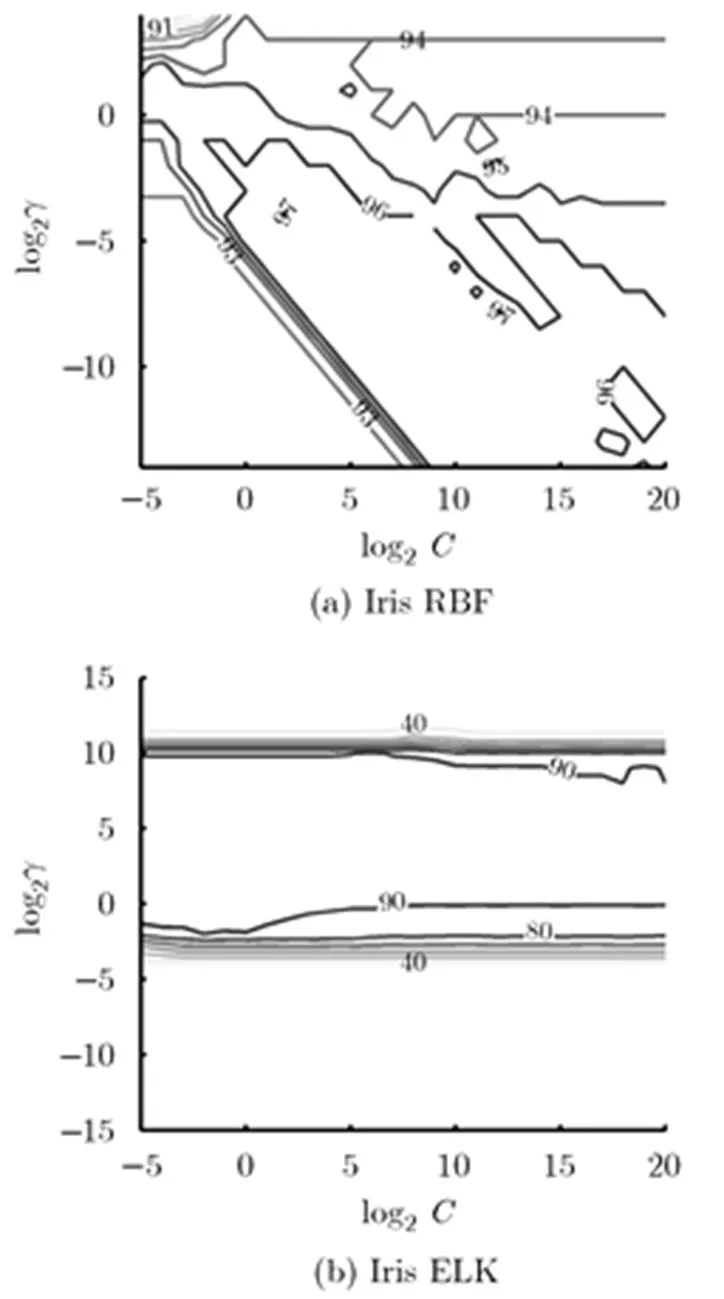
图 7 UCI数据集使用RBF和ELK的参数选择效果对比
6 结论
通过对多尺度重采样过程建模,从理论上导出了时域瞬态信号的局部加权函数,并将这种具有显著中心权重的正对称分布函数发展为一种类指数分布核函数(ELK)。ELK既具有稳定的强局域性,也在一定程度上可以感受大尺度范围的影响。
ELK用于核回归分析,在分析尺度样本的规模,比Gauss核函数具有更好的信号降噪和局部阶跃捕捉能力,综合效果甚至优于LOWESS方法。ELK用于SVM分析时,比使用RBF时更为细致的分类超平面,整体上具有更佳的分类效果,但数据集分类不良时需要更多的支持向量。此外,ELK在一定区域内对于罚函数的变化不敏感,有助于减少参数选择所需的计算量。ELK对局域信号的捕捉能力,以及其形状仅由分析尺度单参数决定的性质,使得该函数的尺度选择上物理意义明确。这一性质有助于这类核函数在其他诸如模式识别、聚类分析等领域的应用中得到推广。
[1] SMOLA A J and SCHLKOPF B. On a kernel-based method for pattern recognition, regression, approximation, and operator inversion[J]., 1998, 22(1): 211-231. doi: 10.1007/PL00013831.
[2] KOHLER M, SCHINDLER A, and SPERLICH S. A review and comparison of bandwidth selection methods for kernel regression [J]., 2014, 82(2): 243-274. doi: 10.1111/insr.12039.
[3] DAS D, DEVI R, PRASANNA S,Performance comparison of online handwriting recognition system for assamese language based on HMM and SVM modelling[J].&, 2014, 6(5): 87-95. doi: 10.5121/csit.2014.4717.
[4] HASTIE T and LOADER C. Local regression: Automatic kernel carpentry[J]., 1993, 8(2): 120-143. doi: 10.1214/ss/1177011002.
[5] Schölkopf B, Smola A, and Müller K R. Nonlinear component analysis as a kernel eigenvalue problem[J]., 1998, 10(5): 1299-1319. doi: 10.1162/ 089976698300017467.
[6] BUCAK S S, JIN R, and JAIN A K. Multiple kernel learning for visual object recognition: A review [J]., 2014, 36(7): 1354-1369. doi: 10.1109/TPAMI.2013.212.
[7] BACH F R, LANCKRIET G R, and JORDAN M I. Multiple kernel learning, conic duality, and the SMO algorithm[C]. Proceedings of the Twenty-first International Conference on Machine Learning, Banff, Canada, 2004: 1-6. doi: 10.1145/1015330.1015424.
[8] 吴涛, 贺汉根, 贺明科. 基于插值的核函数构造[J]. 计算机学报, 2003, 26(8): 990-996.
WU Tao, HE Hangen, and HE Mingke. Interpolation based kernel function’s construction[J]., 2003, 26(8): 990-996.
[9] JAIN P, KULIS B, and DHILLON I S. Inductive regularized learning of kernel functions[C]. Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 2010: 946-954.
[10] ZHANG L, ZHOU W, and JIAO L. Wavelet support vector machine[J].,,,:, 2004, 34(1): 34-39. doi: 10.1109/TSMCB.2003.811113.
[11] NADARAYA E A. On estimating regression[J].&, 1964, 9(1): 141-142. doi: 10.1137/1109020.
[12] Wasserman L著, 吴喜之译. 现代非参数统计[M]. 北京: 科学出版社, 2008: 163-179.
[13] WATSON G S. Smooth regression analysis[J].:,, 1964, 26(4): 359-372.
[14] CRISTIANINI N and SHAWE-TAYLOR J. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods[M]. Cambridge: Cambridge University Press, 2000: 93-112.
[15] VLADIMIR V N and VAPNIK V. Statistical Learning Theory[M]. New York: Wiley, 1998: 293-394.
[16] CHANG C C and LIN C J. LIBSVM: A library for support vector machines[J]., 2011, 2(3): 27. doi: 10.1145 /1961189.1961199.
[17] REN Y and BAI G. Determination of optimal SVM parameters by using GA/PSO[J]., 2010, 5(8): 1160-1168. doi: 10.4304/jcp.5.8.1160-1168.
[18] SARAFIS I, DIOU C, and TSIKRIKA T. Weighted SVM from click through data for image retrieval[C]. 2014 IEEE International Conference on Image Processing (ICIP 2014), Paris, 2014: 3013-3017. doi: 10.1109/ICIP.2014.7025609.
[19] SONKA M, HLAVAC V, and BOYLE R. Image Processing, Analysis, and Machine Vision[M]. Kentucky: Cengage Learning, 2014: 257-749. doi: 10.1007/978-1-4899-3216-7.
[20] SELLAM V and JAGADEESAN J. Classification of normal and pathological voice using SVM and RBFNN[J]., 2014, 5(1): 1-7. doi: 10. 4236/jsip.2014.51001.
[21] 高晋占. 微弱信号检测[M]. 北京: 清华大学出版社有限公司, 2004: 154-299.
GAO Jinzhan. Weak Signal Detection[M]. Beijing: Tsinghua University Press Ltd., 2004: 154-299.
[22] MERCER J. Functions of positive and negative type, and their connection with the theory of integral equations[J].,, 1909, 209(456): 415-446. doi: 10.1098/rsta.1909. 0016.
[23] MARRON J and CHUNG S. Presentation of smoothers: The family approach[J]., 2001, 16(1): 195-207. doi: 10.1007/s001800100059.
[24] LICHMAN M. UCI machine learning repository[OL]. http://archive.ics.uci.edu/ml. 2013.
Design of An Exponential-like Kernel Function Based on Multi-scale Resampling
Hu Zhanwei①②Jiao Liguo③Xu Shengjin①Huang Yong②
①(,,,100084,),②(&,621000,),③(,163311,)
Based on multi-scale resampling, an Exponential-Like Kernel (ELK) function is designed, and evaluated with local feature extraction in kernel regression and Support Vector Machine (SVM) classification. The ELK is a one-parameter kernel, whose distribution is controlled only by the resolution of analysis. With block and Doppler noisy signals, Nadaraya-Watson regression with ELK mainly shows more noise and step error than with Gaussian kernel, it also has better precision and is more robust than LOcally WEighted Scatterplot Smoothing (LOWESS). Data sets from the UCI Machine Learning Repository used in SVM test demonstrate that, ELK has nearly equal classification accuracy as RBF does, and its locality results in more detailed margin hyperplanes, in consequence, a big number of support vectors in low classification accuracy situation. Moreover, the insensitivity of ELK to the adjustive coefficient in kernel methods shows the potential to facilitate the parameter optimization progress. ELK, as a single parameter kernel with significant locality, is hopefully to be extensively used in relative kernel methods.
Multi-scale resampling; Nadaraya-Watson regression; Support Vector Machine (SVM); Exponential- Like Kernel (ELK) function
TN911.7
A
1009-5896(2016)07-1689-07
10.11999/JEIT151101
2015-09-25;改回日期:2016-05-03;网络出版:2016-06-03
徐胜金 xu_shengjin@tsinghua.edu.cn
国家自然科学基金(11472158)
The National Natural Science Foundation of China (11472158)
胡站伟: 男,1984年生,工程师,博士生,研究方向为实验流体力学、信号处理.
焦立国: 男,1970年生,高级工程师,研究方向为信号处理、防洪工程.
徐胜金: 男,1969年生,副教授,博士生导师,研究方向为实验流体力学、流固耦合.
黄 勇: 男,1973年生,副研究员,研究方向为流动控制和动力模拟.
