分数阶Chen系统的控制与反相延迟同步

吉枳霖，郑永爱

（扬州大学江苏扬州225127）

分数阶Chen系统的控制与反相延迟同步

吉枳霖，郑永爱

（扬州大学江苏扬州225127）

分数阶混沌系统在保密通信和振荡器设计等领域有着巨大的应用前景。利用分数阶线性系统的稳定性理论分析了分数阶Chen混沌系统在平衡点处的局部稳定性。设计线性反馈控制并依据分数阶Routh-Hurwitz准则实现了分数阶Chen系统的混沌控制，提供了抑制混沌到不稳定平衡点的充分条件。结合反相同步和延迟同步，提出了分数阶系统的反相延迟同步，并设计相应的非线性控制器实现了分数阶Chen系统的反相延迟同步。数值仿真结果表明了该方法的有效性和可行性。

分数阶Chen系统；混沌控制；分数阶赫尔维茨判据；反相延迟同步

分数阶微积分起源于17世纪，其发展几乎与整数阶微积分具有同样长的历史。分数阶微积分实际是整数阶微积分的推广，分数阶微积分的记忆性和遗传性更能反映系统呈现的工程物理现象，从而促进了分数阶系统的研究和发展。

由于分数阶混沌系统在保密通信和振荡发生器设计等领域有着巨大的应用前景，分数阶混沌系统的控制与同步已成为混沌和控制领域的研究热点。随着对分数阶混沌理论的深入研究，人们从不同角度提出了多种分数阶混沌系统控制和同步的方法，例如，利用分数阶Routh-Hurwitz准则和选择特定的线性反馈控制器，文献［1］控制分数阶Newton-Leipnik系统到它的平衡点；进一步结合分数阶稳定性理论，实现了分数阶Newton-Leipnik系统的混合投影同步。结合广义T-S模糊模型和自适应调节机制，文献［2］提出了控制分数阶混沌系统的一种简单但非常有效的方法。基于分数阶系统稳定性理论和非线性动力学理论，文献［3］构造出相应的非线性控制器，实现了两个维数不同，分数阶次不相等异结构混沌系统与超混沌系统的完全同步与反相同步。通过设计非线性时延观察器，文献［4］分别实现了整数阶Rossler混沌系统和Chua混沌系统的延迟同步。基于分数阶线性系统的稳定性理论，结合反馈控制和主动控制方法，文献［5］提出了实现分数阶混沌系统延迟同步的一种新方法。

文中首先利用分数阶线性系统的稳定性理论分析了分数阶Chen混沌系统在平衡点处的局部稳定性。设计线性反馈控制实现了对分数阶Chen系统的混沌控制，并利用分数阶Routh-Hurwitz准则求出了控制参数的取值范围，避免了每取一组值就要代入公式进行验算，加强了取值的明确性。然后，再结合反相同步和延迟同步提出了分数阶反相延迟同步。通过设计非线性反馈控制器实现了分数阶Chen系统的反相延迟同步，从理论上证明了该方案的可行性。利用预估-校正算法［6-7］对分数阶Chen系统进行的数值模拟验证了该方案的有效性。

1　分数阶微积分定义

尽管分数阶微积分有Riemann-Liouville（R-L）定义和Caputo定义两种常用定义，下面是经常使用的Caputo定义：

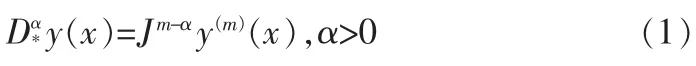
在这里m是不小于α的第一个整数，y（m）表示m阶导数，yβ表示如下β阶R-L积分算子：通常表示α阶微分算子，Γ（·）是Gamma函数。

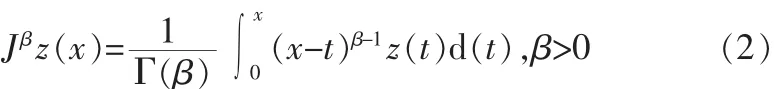
2　分数阶Chen混沌系统的控制

描述如下三维分数阶Chen混沌系统：

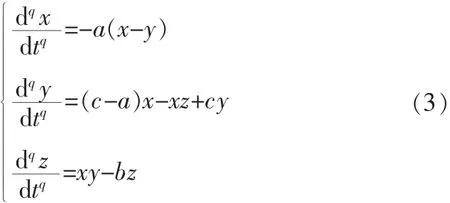
这里0＜q≤1。利用分数阶微分方程的预估-校正算法进行数值仿真。取a=35，b=3，c=28，q=0.9，初始值为（x，y，z）=（2，1，3），时间步长h=0.01，图1呈现了Chen混沌系统（3）的混沌吸引子。

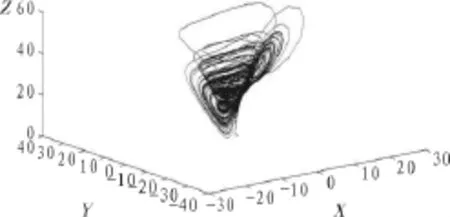
图1　分数阶Chen系统的吸引子相空间

下面给出分数阶Routh-Hurwitz准则，考虑三维分数阶系统：

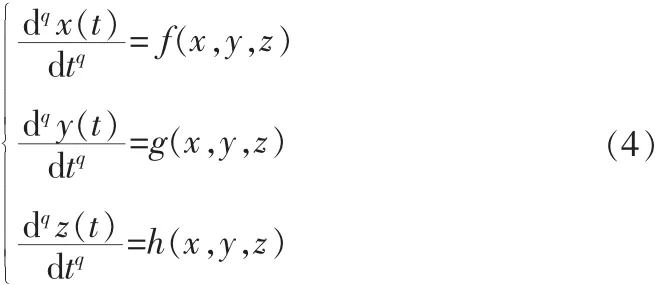
其中q∈（0，1］。上述系统（4）在平衡点处的Jacobian矩阵为：

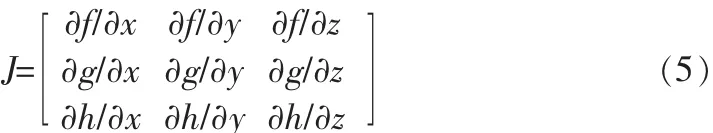
在平衡点处的特征方程为：

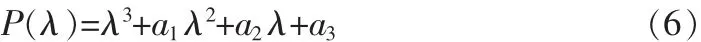
判别式为：

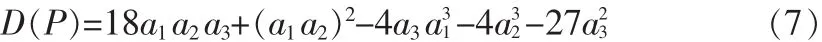
引理1：分数阶系统（4）是局部渐近稳定的当且仅当在平衡点处的Jacobian矩阵（5）的任意特征值λ满足|arg（λ）|＞

引理2（分数阶Routh-Hurwitz准则）［8］：

（i）若D（P）＞0，则系统（4）的平衡点是局部渐近稳定的充分必要条件是a1＞0，a3＞0，a1a2-a3＞0。

（ii）若D（P）＜0，a1≥0，a2≥0，a3＞0，则当α＜2/3时，系统（4）的平衡点是局部渐近稳定的；若D（P）＜0，a1＜0，a2＜0，a＞2/3，则方程（6）的所有根满足

（iii）若D（P）＜0，a1＞0，a2＞0，a1a2-a3=0，则对于0＜q≤1，系统（4）的平衡点是局部渐近稳定的。

（iv）系统（4）的平衡点局部渐近稳定的必要条件是a3＞0。

我们首先来讨论系统（1）的平衡点的稳定性。当参数a= 35，b=3，c=28时，系统（3）有3个平衡点：

性质1：当参数a=35，b=3，c=28时，对于任意的q∈（0，1］，系统（3）的平衡点E1始终是不稳定的。

证明:当参数a=35，b=3，c=28时，系统（3）在平衡点E1处的特征多项式为：

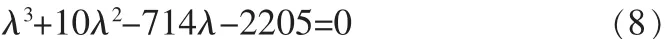
式（8）的特征值为：λ1=-30.8359，λ2=23.8359，λ3=-3.0000。因为λ2＞0，根据引理1，对于任意的q∈（0，1］，平衡点E1是不稳定的。

性质2：当参数a=35，b=3，c=28时，如果q＜0.8244，系统（3）的平衡点E2或者E3是渐近稳定的；如果q＞0.8244，系统（3）的平衡点E2或者E3是不稳定的。

证明：当参数a=35，b=3，c=28时，根据系统（3）的平衡点E2或者E3得到特征多项式：

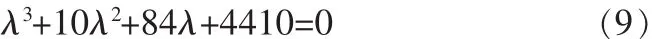
上式（9）的特征值为：

这里λ1是个负实数。根据引理1，当q＜2|arg（λi）|/π≈0.8244（i=2，3）时，系统（3）的平衡点E2或者E3是渐近稳定的。如果q＞0.8244，系统（3）的平衡点E2或者E3是不稳定的。

下面我们利用反馈控制和分数阶Routh-Hurwitz准则来抑制三维分数阶Chen混沌系统到它的一个不稳定的平衡点，三维分数阶Chen混沌受控系统描述如下：

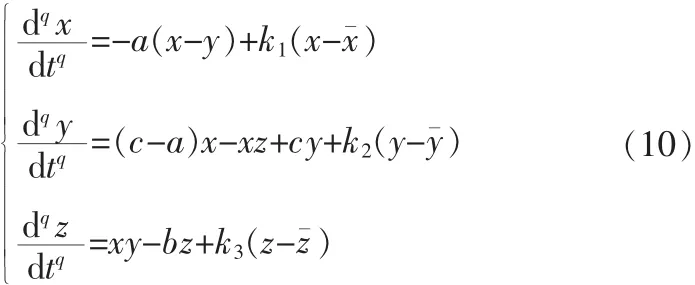
其中k1，k2，k3为控制参数，是系统（3）的平衡点。这里我们仅利用线性反馈来稳定系统（3）的平衡点E1（0，0，0）。当a=35，b=3，c=28，系统（10）在平衡点E1（0，0，0）处的Jacobian矩阵为：

相应的特征多项式为：

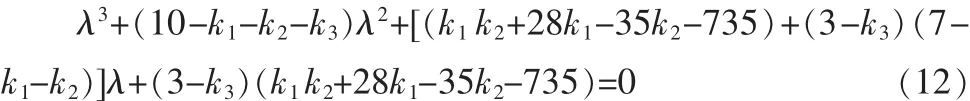
判别式为：

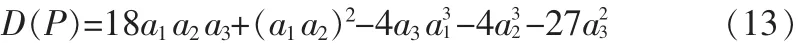
其中

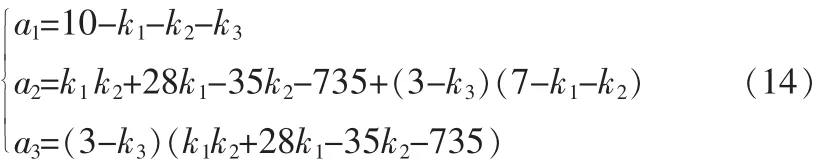
虽然这里我们很难同时求出3个控制参数的取值范围，但是我们经过计算可以先给两个参数赋值，利用分数阶Routh-Hurwitz准则求出第三个控制参数的取值范围。这样避免了每取一组值就要代入公式进行验算，加强了取值的明确性。所以将k1=20，k2=-13代入（14）式中，经过严格的数学计算，如果要满足D（P）＜0，a1＞0，a2＞0，a1a2=a3成立，则k3＜3即可。

3　分数阶Chen系统的反相延迟同步

考虑分数阶Chen混沌系统（3）为驱动系统，那么响应系统为：

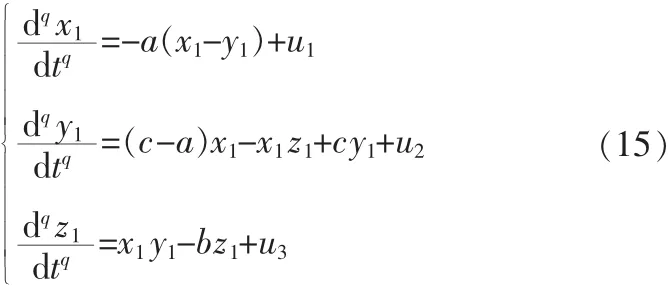
这里u1，u2，u3为控制器。对于系统（3）与（15），如果存在常数τ使得则称分数阶Chen混沌系统（3）与（15）达到分数阶反相延迟同步。其中X（t）=（x（t），y（t），z（t））T，Y（t）=（x1（t），y1（t），z1（t））T分别为系统（3）和（15）的状态向量。结合反馈控制和主动控制方法，设计控制器为：

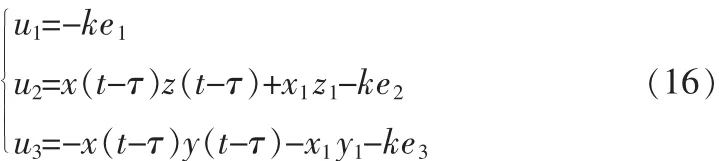
误差系统为：

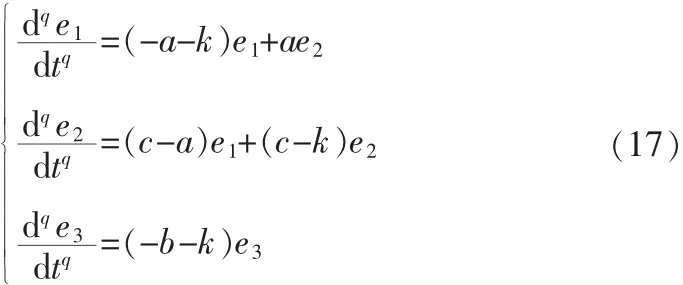
当a=35，b=3，c=28时，通过计算要使D（P）＞0，a1＞0，a3＞0，a1a2-a3＞0成立，则k＞23.8359。根据Routh-Hurwitz判据条件，当k＞23.8359时，误差系统（17）在平衡点E1（0，0，0）处渐近稳定，即驱动系统（3）和响应系统（15）实现了分数阶反相延迟同步。

4　数值仿真

利用分数阶微分方程的预估-校正算法，对分数阶Chen混沌系统的控制和反相延迟同步进行数值仿真，其中选取步长h=0.01，q=0.9，a=35，b=3，c=28。首先对分数阶Chen混沌系统的不稳定平衡点E1（0，0，0）进行混沌控制。选取初始点x（0）=2，y（0）=1，z（0）=3。参数k1=20，k2=-13，k3=2，q=0.9。仿真结果如图2所示。其次对驱动系统（3）和响应系统（15）的反相延迟同步进行仿真。当k=25，时间t=40 s，延迟时间τ=10 s，q=0.9，步长h=0.01，系统（3）和（15）的初值分别为x（0）=（2，1，3）T，y（0）=（3，3，6）T时，图3给出了分数阶线性误差系统（17）中分数阶反相延迟同步误差收敛曲线。

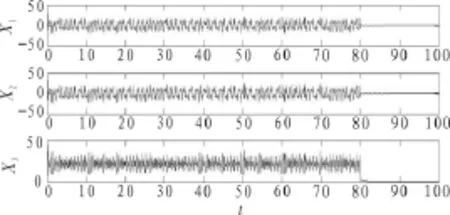
图2　系统（10）在平衡点E1（0，0，0）控制结果

图3　同步误差系统的时间序列曲线

5　结论

本文以分数阶Chen系统为例，利用分数阶Routh-Hurwitz准则和线性反馈控制混沌系统到平衡点。通过对分数阶Chen混沌系统构造相应的非线性控制器实现了分数阶Chen系统反相延迟同步。数值仿真结果验证了该方法的有效性和可行性。该方法同样可以简洁地实现高维分数阶混沌系统的反相延迟同步。

［1］ZHANG K，WANG H，FANG H.Feedback control and hybrid projective synchronization of Sci［J］.Numer Simulat，2012（17）:317-328.

［2］ZHENG Y A，NIAN Y B，WANG D J.Controlling fractional order chaotic systems based on Takagi-Sugeno fuzzy model and adaptive adjustment mechanism［J］.Physics Letters A，2010（2）:125-129.

［3］董俊，张广军，姚宏，等.分数阶异结构超混沌系统完全同步与反相同步控制［J］.动力学与控制学报，2014（2）:119-126.

［4］LI C D，LIAO X F.Lag synchronization of Rossler ctsystem and Chua circuit via a scalar signa［J］.Physics Letters A，2004，329:301-308.

［5］王德金，郑永爱.分数阶混沌系统的延迟同步［J］.动力学与控制学报，2010（8）:338-341.

［6］K Diethelm，N J Ford，A D Freed.A predictor-crrector approach for the numerical solution of Fractional differentialequations［J］.Nonlinear Dynamics，2002（29）:3-22.

［7］K Diethelm.An algorithm for the numerical solution of differential equations of fractional order［J］.Electron Trans Numer Anal，1997（5）:1-6.

［8］Matignon D.Stability results for fractional differential equations with applications to control processing［J］.Computational Engineering in Systems And Application Multi Conference，1996（2）:963-968.

Control and inverse lag synchronization of the fractional order Chen system

JI Zhi-lin，ZHENG Yong-ai
（Yangzhou University，Yangzhou 225127，China）

Fractional order chaotic system has a very great prospect in the fields of secure communication and oscillator design. In this article the local stability of the fractional order Chen chaotic system at various equilibrium points is analyzed using the stability theory of fractional order linear systems.Feedback control is designed to realize chaos control of the fractional order Chen system according to fractional order Routh-Hurwitz criterion，and provide the sufficient conditions suppressing chaos to a unstable equilibrium point.Combining inverse synchronization with lag synchronization，a novel fractional order inverse lag synchronization method is proposed.A corresponding nonlinear controller is designed to reach the inverse lag synchronization of fractional order Chen system.Numerical simulation shows effective and feasibility of the proposed method.

fractional order Chen system；chaos control；fractional routh-hurwitz criteria；inverse lag synchronization

TN93

A

1674－6236（2016）12-0070-03

2015-07-01稿件编号：201507007

吉枳霖（1987—），男，江苏南通人，硕士研究生。研究方向：混沌控制。