一种多源异构数据融合方法及其应用研究

姜建华，洪年松，张广云

（1.广东科学技术职业学院计算机工程学院，广东珠海519090；

2.浙江工贸技术职业学院信息传媒学院，浙江温州325003）

一种多源异构数据融合方法及其应用研究

姜建华1，洪年松2，张广云1

（1.广东科学技术职业学院计算机工程学院，广东珠海519090；

2.浙江工贸技术职业学院信息传媒学院，浙江温州325003）

针对基于多源数据融合的多用户决策问题，建立了多源异构数据融合模型，研究了基于三角模糊数的异构数据统一量化表示方法，采用有序加权平均算子融入决策者的偏好，设计了一种支持多用户决策的多源异构数据融合算法。实际应用表明，本文设计的算法能解决多源异构数据在结构和语义上的模糊性、差异性和异构性等问题，通过在数据融合过程中考虑决策者偏好，提高了多用户决策结果的可靠度。

多源异构数据；数据融合；三角模糊数；有序加权平均

数据融合本质上是对来自多方数据的协同处理，以达到减少冗余、综合互补和捕捉协同信息的目的，该技术已成为数据处理、目标识别、态势评估以及智能决策等领域的研究热点。文献［1］基于统计和人工智能方法，研究了多传感器数据融合技术；文献［2］研究了移动地理信息系统中的多源异构数据组织与管理，建立了多源异构数据融合模型；文献［3］将无线传感器网络和数据融合技术相结合，提出了一种Kalman滤波分批估计融合算法；文献［4］研究了物网联网环境下海量多源异构数据融合方法，并成功应用于目标定位跟踪过程中；文献［5］研究了高铁信号系统基于异构数据融合的智能维护决策架构，提高了决策的准确性和有效性；文献［6］研究了数字矿山建设过程中的多源异构数据融合技术，保证了数字矿山建设中基础信息平台的安全稳定和高效。

数据的表示方式除了数值外，还存在着语言或符号等其他描述形式，多种描述导致了数据信息在结构和语义上的模糊性、差异性和异构性。另一方面，决策过程需要综合考虑多方面的异构数据信息，并通过对数据信息的融合处理来制定最终决策。因此，文中从异构数据的特点出发，研究一种支持多用户决策的多源异构数据融合方法。

1　多源异构数据融合模型

1.1多源异构数据融合方法

数据融合按操作级别分为数据级融合、特征级融合以及决策级融合。本文研究多数据源在决策级上的融合，其方法主要有权重平均法、D-S证据理论和投票表决等。

1）权重平均法

采用Σwitij计算各数据源对决策的支持度值，wi为数据源i权重，tij为数据源i对第j决策的支持度，该方法根据支持度的大小判断决策方案的优劣，具有易操作、考虑了数据源的重要程度等特点，但权重的确定包含着主观因素。

2）D-S证据理论

将待识别对象所有可能结果构成的空间定义

为识别框架D，其子集记为2D，∀A⊆D，定义：

m:2D→［0，1］

其中：m（φ）=0，ΣA⊆2Dm（A）=1，φ为空集，则m为2D上的基本概率分配函数（BPAF），它实际上是根据证据对D的子集进行信任度分配。

实际中往往针对同一问题因证据不同而得到不同的mi，考虑所有证据后的m可通过下式得到：

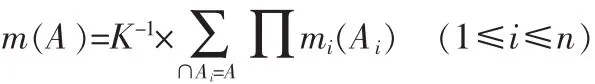
D-S证据理论建立在BPAF基础上，能处理由“不知道”所引起的不确定性，缺点是D中元素必须满足互斥条件，且当BPAF过多时计算很复杂。

3）投票法

将各个数据源看作投票者，通过比较各决策获得的票数以定优劣，计算方法为：

Sup（ai）=F（Supj（ai））

其中：ai为第i决策，Sup（ai）为其得“票数”；Supj（ai）为第j数据源对ai的支持度，若支持则取1，否则为0，函数F可定义为连加求和。

针对多源异构数据的BPAF难以确定，投票法不能区分票数相同的决策，在考虑决策者偏好的情况下，文中采用OWA方法对数据进行融合处理。

1.2多源异构数据融合结构

文献［7］提出一种多数据源的融合结构，如图1所示。该数据融合过程考虑了表达用户需求的特征因素和信息的可靠程度，利用上下文知识和领域知识、采用投票法解决数据冲突等问题。

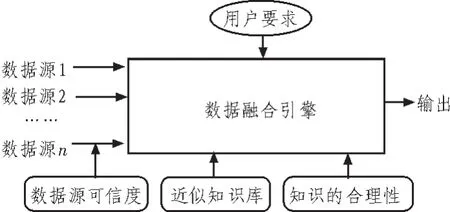
图1　多源数据源融合结构

针对上述模型，本文设计了一种支持多用户决策的多源异构数据融合结构模型，如图2所示。模型中的数据融合引擎包括数据仓库、决策支持度计算、OWA算子权重向量计算和数据转换与排序4个模块，具体描述如下。

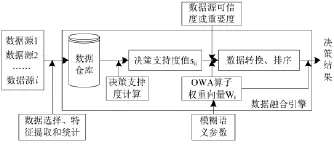
图2　多源异构数据融合模型

1）数据仓库通过数据选择、特征提取和统计等操作实现对数据的集成、消除数据的异构性和差异性，为后续的数据处理提供数据源；

2）决策支持度计算模块根据决策属性从数据仓库获取相关维度的数据，并计算各数据源对决策的支持度值sij（数据源i对第j决策的支持度）；

3）OWA算子权重向量计算模块根据决策者提供的模糊语义原则计算出OWA权重wi，模糊语义参数的选择体现了决策者对数据源的偏好态度；

4）数据转换与排序根据决策者提供的数据源可信度或重要度，结合OWA权重向量wi对sij进行转换，并将转换后的结果按大小顺序排序，最后将排序后的结果与通过求和计算出最终决策值。

2　多源异构数据融合算法

2.1数据类型及其特点

对数据可以从数量和质量两方面进行描述，数量方面通过数值表示，而质量方面通过语言变量进行描述［8］。根据数据描述方式的不同，本文将数据分为定性和定量两类，重点研究随机变量、二值型、语言程度和采用词汇术语的4类描述，如表1所示。

表1　数据描述方式

大样本情况下，随机变量服从正态分布，记为：X～（μ，σ2），μ为期望，σ为标准差，且满足：P（μ-3σ＜X＜μ+3σ）=0.9974。

二值型数据用于描述对事实的肯定或否定，取值空间大多为｛1，0｝或｛True，False｝。

表示程度的数据一般采用汉语程度副词来表示，如很好、非常差等，程度等级大多采用7或9个标准。

基于词汇术语的数据采用词汇空间中规定的词汇或术语给出事物定性的描述，词汇个数视具体情况而定。

2.2基于三角模糊数的支持度计算

考虑到多源数据描述中存在着模糊性，可采用三角模糊数计算数据对决策的支持度值。

1）随机性数据的转换

设：x0=u-3σ

若随机变量的取值越大，其对决策的支持度也越大。将区间［μ-3σ，μ+3σ］进行n等分，则随机数据向支持度的转换可定义为：

若随机变量的取值越小，其对决策方案的支持度越大，则支持度定义为：

s′（x）=（1，1，1）-s（x）

2）二值型数据的转换

二值型数据采用1或0进行描述，若数据源中取1和0的个数分别为n和m，且支持度以取值1为依据，则数据源对决策的支持度定义为：

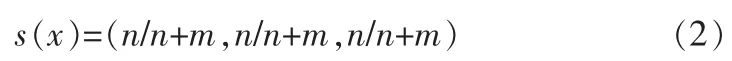
3）程度类数据的转换

描述对象好坏程度一般可采用7或9标准，本文采用7等级标准。程度副词的表示分正比型（效率越高越好）和反比型（费用越高越差），则各等级对决策的支持度可量化如表2所示的数据。

表2　程度类型数据的支持度

4）词汇术语数据的转换

设词汇空间w包含n个术语，对词汇按对决策支持度从低到高排序为：w=｛w0，w1，…，wn-1｝，则支持度定义为：

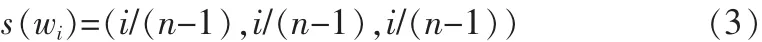
2.3OWA的权重向量计算

设：F:Rn→R，有一个与F相关联的n维加权向量w=（w1， w2，…，wn），wi∈［0，1］，1≤i≤n，且使得：

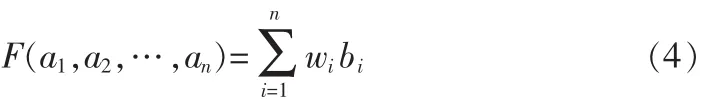
其中：bi是ai中第i个最大的元素，则F称为n维OWA算子。

OWA权向量w=（w1，w2，…，wn）由下式确定：

其中：i=1，2，…，n，f为模糊语义量化算子，定义为：

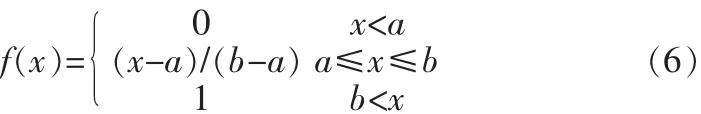
其中：x，a，b∈［0，1］。

此外，OWA算子还定义了反映决策者乐观态度的度量算子：

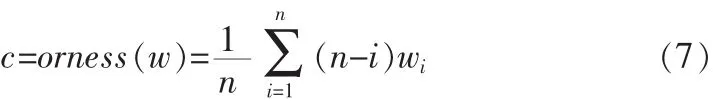
2.4数据融合算法

设有n个决策：A=（A1，A2，…，An），m个数据源：S=（S1，S2，…，Sm），各数据源的可信度（或重要度）为pi，数据融合算法描述如下：

第1步：计算数据源对决策的支持度；

从数据仓库中提取数据，根据数据的不同类型，按1.2部分将其转换为对决策的支持度：

其中：Sij为第i数据源对第j决策目标的支持度，（aij，bij，cij）为支持度的三角模糊数表示，且：0≤aij≤bij≤cij≤1。

第2步：确定OWA算子权重向量；

根据决策者的偏好，选择适当的模糊语义量化准则，确定式（6）中的参数和的值。模糊语义原则一般为“大多数”、“至少一半”或“尽可能多”，它们的参数值分别为（0.3，0.8）、（0，0.5）和（0.5，1），根据参数可确定出模糊语义量化算子f（x）。

根据f（x），通过式（5）求得OWA权重向量w=（w1，w2，…，wn），n为数据源个数，并按式（7）求得c的值。

第3步：根据各数据源可信度（或重要度）pi和支持度值sij对sij进行转换；

为了利用OWA权重向量，需要根据pi与sij对各决策值进行转换并按大小顺序排序，转换方法采用模糊判决法。

设：

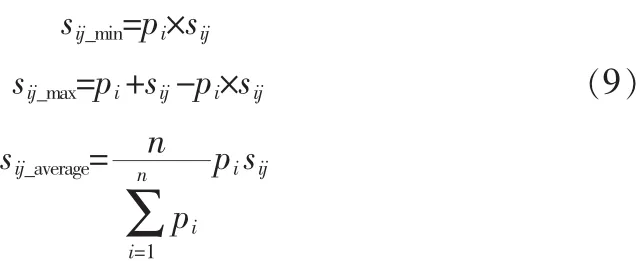
定义：当c≤0.5时

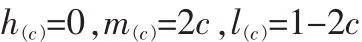
当c≥0.5时

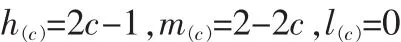
则经过转换后的决策支持度值表示为：

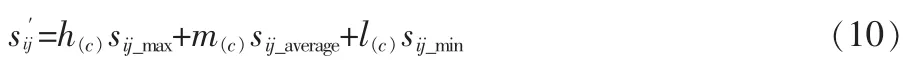
第4步：依据OWA算子权重向量和转换后的支持度对数据进行融合，并计算各决策的最终决策值；

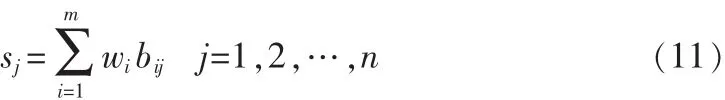
其中：bij为中第i个最大元素。

第5步：根据实际问题按决策值大小做出决策。

3　应用实例

以某公司为了提高其产品市场竞争力，拟从同一品牌下多种型号产品中挑选一款进行重点打造为例。假设现有5种型号的产品，型号为A1、A2、A3、A4、A5，公司可搜集到的数据包括产品市场需求预测、产品使用后的反馈、产品参数、产品使用历史状态、产品故障以及同行专家提供的建议等数据信息。针对各型号产品从市场需求评价a1、平均年故障次数a2（μ= 3.5，σ=0.8）、最长无故障时间a3（μ=12.28，σ=2.53）、经济性a4、用户评价a5和专家建议a66个方面进行比较。通过对数据进行整理，得到各个指标数据信息如表3所示。

1）对表中各数据描述类型分析知：a1和a4为程度型，按表2进行变换；a2和a3为随机变量型，按式1进行变换；n且取15；a5为二值型数据（表中数据为用户评价为“好”的比例），按式2进行变换；a6为词汇空间描述型，按式（3）进行变换。则对表3中统一量化处理的结果如表4所示。

2）选择“大多数”作为模糊语义原则，式（6）中的和分别为0.3和0.8，根据式（5）和式（6）可得到OWA权重向量：w=（0，0.067，0.33，0.33，0.27，0），

计算出权重向量后，根据式（7）求得：

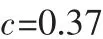
3）根据pi和sij结合式（9）和式（10）对表4中的数据进行转换，转换结果如表5所示。

4）对表5中的每列按第二个数据值从大到小排序，并根据式（11）进行计算的结果如表6所示。

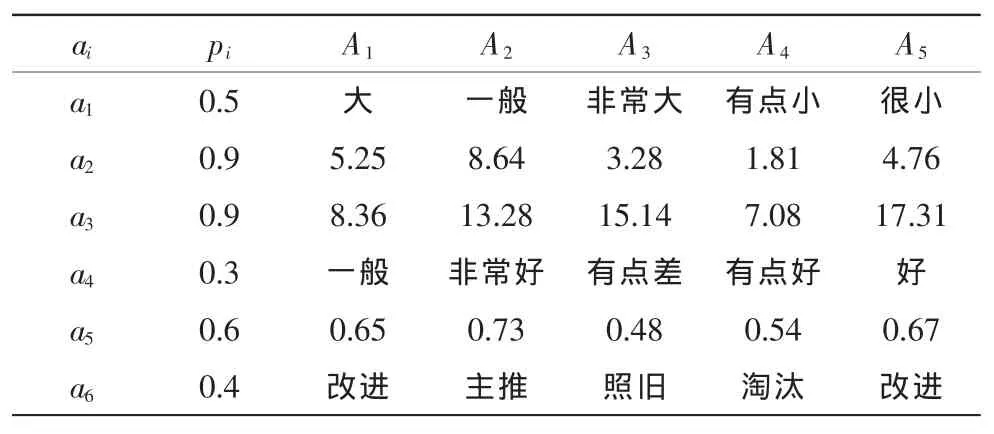
表3　各产品支持度和数据源可信度

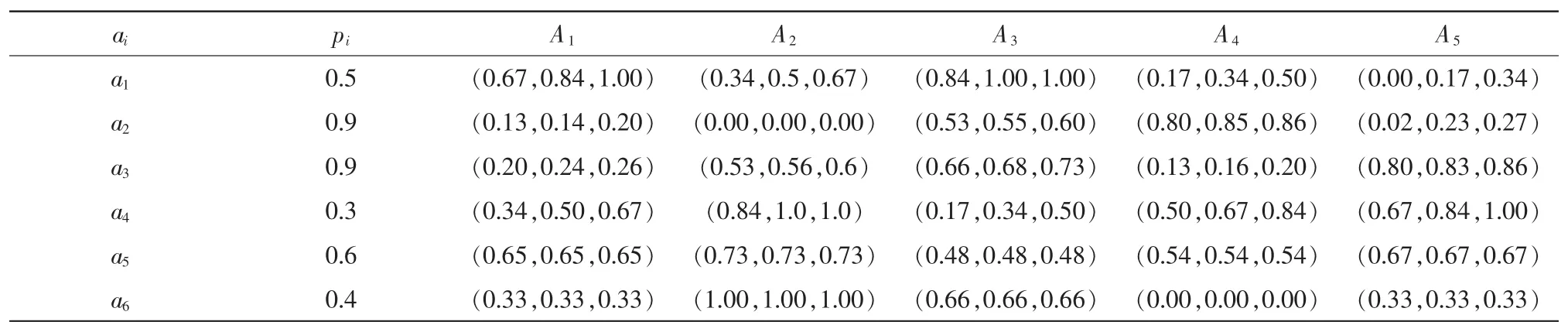
表4　各产品支持度的统一量化结果

表5　数据变换后的结果

表6　最终决策结果

5）从表6可以看出，A3产品的支持度最高，则重点考虑第A3型号产品。

4　结束语

文中建立了多源异构数据融合结构模型，研究了基于三角模糊数的异构数据量化处理方法，基于OWA算子设计了数据融合算法，实际应用证明算法是可行的和有效的。本文的研究为建立智能决策支持系统提供了一种可行的方案，对其他类似的数据处理和融合具有一定的借鉴作用。

［1］Nakamura E R，Loureiro A A F，Frery A C.Information fusion for wireless sensor networks:Methods，models and classifications［J］.ACM Computer SURV，2007，39（A9）:1-55.

［2］李文闯，章永平，潘瑜春.移动地理信息系统中的多源异构数据融合模型［J］.计算机应用，2012，32（9）:2672-2678.

［3］凌云.基于物联网的异构传感数据融合方法研究［J］.计算机仿真，2011，28（11）:138-140.

［4］胡永利，朴星霖，孙艳丰，等.多源异构感知数据融合方法及其在目标定位跟踪中的应用［J］.中国科学，2013，43（10）: 1288-1306.

［5］徐田华，杨连报，胡红利，等.高速铁路信号系统异构数据融合和智能维护决策［J］.西安交通大学学报，2015，49（1）: 72-78.

［6］李国清，胡乃联，陈玉民.数字矿山中多源异构数据融合技术研究［J］.中国矿业，2011，20（4）:90-93.

［7］WANG Guang-yun，LI Wei-hua，HUA Wen-jian，et al.A method for heterogeneous uncertain information fusion and its application［C］.International Conference on Signal Processing Proceedings，2004（3）:2253-2256.

［8］俞黎阳，王能，张卫.无线传感器网络中基于神经网络的数据融合模型［J］.计算机科学，2008，12（35）:43-47.

Research on multi-source heterogeneous data fusion and its application

JIANG Jian-hua1，HONG Nian-song2，ZHANG Guang-yun1
（1.School of Computer Engineering&Technology，Guangdong Institute of Science&Technology，Zhuhai 519090，China；2.College of Information and Communications，Zhejiang Industry&Trade Polytechnic，Wenzhou 325003，China）

As to the multi-source data fusion based multi-user decision，a model of multi-source heterogeneous data fusion was designed.Triangular fuzzy number based uniform quantity description of multi-source data was researched.The ordered weight average（OWA）was used to deal with the preference of decision-maker and a data fusion algorithm for decision making was designed.At last，practical application shows the algorithm can solve the problems of semantic ambiguity，difference and heterogeneity of multi-source heterogeneous data，and the reliability of decision results was improved by considering data maker's preference into the process of data fusion.

multi-source heterogeneous data；data fusion；triangular fuzzy number；ordered weight average

TN01

A

1674－6236（2016）12-0033-04

2015-06-24稿件编号：201506219

姜建华（1978—），男，湖北洪湖人，博士研究生，讲师。研究方向：计算机应用技术。