基于谱聚类的高阶模糊时序自适应预测方法

周春楠，黄少滨，迟荣华，李雅，郎大鹏



基于谱聚类的高阶模糊时序自适应预测方法

周春楠，黄少滨，迟荣华，李雅，郎大鹏

（哈尔滨工程大学计算机科学与技术学院，黑龙江哈尔滨 150001）

结合数据特征及分布特点提出一种基于谱聚类的模糊时间序列自适应预测方法。首先基于谱聚类的思想，根据样本数据特征获取其所属论域的个数及范围，实现向模糊时间序列的自适应转化；然后基于Markov概率模型表示模糊时间序列中的模糊关系，从而对多步模糊关系、高阶模糊关系及模糊关系的稳态进行求解；最后获取预测值的可能模糊状态，进而利用去模糊化方法将其还原为预测值。在真实以及人工时间序列数据上的实验表明了所提方法的合理性与有效性。

模糊时间序列；谱聚类；论域划分；Markov概率模型；模糊关系

1 引言

时间序列数据是在自然界、工程技术以及经济社会等领域广泛存在着的一种重要数据类型，如气象上的降水量和气温数据、天文上的太阳黑子数据、经济领域的GDP和股指数据、医学上的心/脑电波序列、移动通信行业的话务流量、复杂工业系统运行过程中的状态监测数据等均属于时间序列数据。对时间序列数据研究的一项主要内容就是时间序列的预测，即根据历史时间序列数据发现数据的内在特性和发展规律，并构造随时间变化的序列模型，然后基于一定的规则推测未来的数据，从而为相应领域的决策提供依据。

时间序列数据包括线性和非线性数据，相应的预测（建模）方法也分为线性方法和非线性方法。其中，线性预测方法主要包括基于传统统计学时间序列随机模型的经典回归分析等方法，而非线性预测方法则主要包括人工智能领域的神经网络、支持向量机等方法。上述回归方法、神经网络方法、支持向量机方法均利用传统的确定性关系表示数据所属的集合，并且过于依赖历史数据的完整性、精确性和确定性；然而历史数据往往是不完整的、不精确的、不确定的。

面对这种时间序列的观测值中包含大量不完整或噪声信息的情况，模糊时间序列（fuzzy time series）[1]引入了模糊理论，将历史数据中的不确定性变量利用模糊变量进行表示，相应的预测方法也被成功地用于多个领域，如学生登记[1~3]、温度[4,5]、电信业务[6]等，其中，在股票预测上的效果尤为明显[7]，而随着成功案例的不断涌现，许多非信息科学领域，如临床医学[8]、环境治理[9]以及旅游[10]等也开始采用模糊方法进行建模和分析。

模糊时间序列预测方法的核心内容是论域的划分和模糊规则的提取，合理有效的方法确保了模型的预测精度。而模糊规则的提取又是以划分论域的结果为基础，针对这一环节，近年来出现了很多关于论域划分问题的改进方法。较具代表性的有以均匀等分为思想的论域划分方法，这种方法相对简单，建模复杂度较低，但是均匀划分不能体现信息的真实分布，预测精度也较低[2~5]。基于启发式来确定论域划分的方法，考虑了划分间隔对预测结果的影响[11]。另外，还有基于自然划分[12]、基于分布密度[13~15]、基于比例的间隔长度[16]、基于遗传算法[17]，基于多变量[18]以及单变量约束的优化算法[19]等方法来划分论域。除了对算法核心内容的改进之外，混合方法也是提高算法效果的有效途径，例如与模糊聚类和神经网络相结合的方法[20,21]，与粒子群优化与支持向量机结合的方法[22]以及与改进的遗传算法相结合的方法[23]。

上述方法大多是以时间序列数据服从均匀分布或短尾分布为假设而提出的。然而进一步的研究发现，真实时间序列数据（特别是经济领域）由于系统的涌现行为更多的是聚集出一种长尾的密度分布，上述方法便缺乏一定的合理性。同时又有研究表明，根据数据的真实分布来确定论域的划分往往能够获得较好的效果，其中尤以基于聚类思想的论域划分方法更为突出，因为它能够发现数据的真实密度分布，进而可获得较高的预测准确性[24]。

例如文献[25,26]基于层次聚类方法获得聚簇，并将其转化为对应论域的间隔细分，然后根据细分的间隔模糊化时间序列，提取模糊关系并构建预测模型。文献[27]则结合基于密度的聚类以及公理模糊集分类技术构建模糊预测模型。即通过聚类产生的聚簇进行论域划分，并基于公理模糊集分类方法构建预测模型。然而这些方法在聚类之前需先对数据进行排序，如此便失去了聚类能够发现数据分布情况的最大优势。文献[28,29]基于模糊C均值（FCM, fuzzy C-means）算法构建模糊时间序列预测模型，根据聚类结果划分论域并提取模糊关系。虽然模糊聚类方法有助于发现时间序列中的模糊关系，但FCM算法需要预先设定聚簇数目，而时序数据的增长会使数据分布密度也发生变化，如此便会导致预测精度的下降。

如前所述，真实的时间序列数据往往呈现长尾分布的现象，这是因为时间序列数据之间存在一定的关联。另外，根据现有的研究成果可知聚类有助于获取数据分布区域，从而能够更准确地进行论域划分，因此聚类结果的准确性影响着模糊时间序列预测的精度。实际上模糊时间序列中数据之间的关联关系可以利用一个关联矩阵来描述，而谱聚类[30]是基于关系矩阵的一种有效聚类算法，同时它不易陷入局部最优，而且能够识别非云状等特殊分布特点的聚簇，因此谱聚类有助于有效划分模糊时间序列中的数据分布情况。

因此，本文提出一种基于谱聚类的模糊时间序列预测方法。首先基于谱聚类对时间序列数据的论域进行划分，实现由原始时间序列向模糊时间序列的自适应转化，并获得对应的模糊集合；然后利用模糊集表示模糊时间序列；对于时序观测值变化的不确定性，提取模糊时间序列中的高阶模糊关系，并引入高阶Markov概率模型描述这种模糊关系，据此对后续数据进行预测。从而使所提模型可在不对数据分布进行假设的基础上，有效地划分原时间序列数据的论域；同时高阶Markov的引入使模型考虑了之前时刻的数据影响后续数据的各种可能性。从论域划分以及模糊关系提取2个方面保证了模型预测的准确性。

2 相关知识

2.1 模糊时间序列定义及表示

模糊集理论最早由Zadeh提出用于处理不确定性问题。Song和Chissom[1]成功地将该理论用于时间序列预测上，其基本思想是根据时间序列的值域确定一个论域及其对应的一种划分，根据划分的论域构建对应的模糊集合，每个划分的隶属度代表了划分的论域在该模糊集中的权重，然后将时间序列的观测值映射为所属论域划分所对应的模糊集，模糊时间序列即为由模糊集表示的时间序列。上述方法的具体定义如下。

2.2 基于谱聚类的自适应论域划分方法

谱聚类是一种非无督学习过程，相对于其他聚类算法，它能够有效解决数据分布复杂的情况，且收敛于全局最优解[30]。当前部分关于谱聚类的研究集中于利用拉普拉斯矩阵的性质，其中，较典型的是基于矩阵摄动理论的谱聚类算法[31]。

基于摄动理论的谱聚类算法，相较于传统谱聚类算法，具有自适应的能力，可自动确定聚簇个数，该方法主要过程如下所述。

1) 计算数据集中各元素间的相似性，构建的相似矩阵，矩阵中的元素根据高斯相似性有。

3) 计算拉普拉斯矩阵的特征值，将其升序排列。

该方法仍遵循谱聚类的基本思想，不同之处在于它对拉普拉斯矩阵的特征值序列进行了判断，即当矩阵的第个特征值相对于其前一个第个特征值变化较大时，则由前个特征向量所构成的特征矩阵所代表的元素间的关系越稳定，因此可利用特征值的差值来确定聚簇的个数，但多大程度的差值可以得到最佳的聚簇个数需要通过计算特征值的方差来判断。

3 基于谱聚类的模糊时间序列自适应预测方法

面对真实时间序列数据中存在大量不完整或噪声信息的情况，本文所提模型的基本思想是利用无监督学习的聚类方法对时间序列数据的论域进行划分并计算模糊集，用模糊集表示原始时间序列数据所对应的模糊时间序列。然后构建原始时间序列数据中的模糊逻辑关系，并由高阶Markov概率转移矩阵对其进行建模。最后计算已知模糊状态在高阶状态转移中发生概率最高的下一状态，并通过去模糊化方法将下一模糊状态还原为下一时刻的预测数值。那么基于谱聚类的模糊时间序列预测方法（SFTP，spectral-based fuzzy time-series prediction）构建的具体方法如下所述。

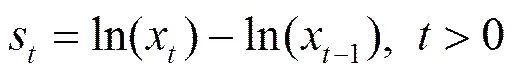
由上述分析可知时间序列数据之间存在一定相似性，在划分论域时需充分考虑它们之间的相似性。谱聚类算法基于对象间的相似矩阵，将聚类问题转化为图划分问题，并且不对数据的分布进行假设。可见谱聚类的特点使其更适合于处理划分论域的问题。那么基于谱聚类确定时间序列论域划分的具体步骤如下。

①计算描述时间序列数据间相似度的相似矩阵，若样本数据对应的趋势变化序列为，那么相似矩阵的元素如式(2)所示，其中，。

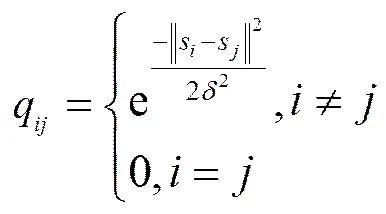
解决图划分问题的有效方法是将其转化为求解对应矩阵的谱分解问题，即根据矩阵的特征值和特征向量对数据集进行划分。同时，由矩阵的摄动理论可知，矩阵的第和个特征值之间的差距越显著，由所选的个特征向量构成的子空间就越稳定。

③获取趋势变化序列的聚类结果。由谱聚类的思想可知，拉普拉斯矩阵对应的特征向量即为嵌入空间中的点，然后利用-means 算法对嵌入空间中的点进行划分，得聚簇集合，其中，。其具体含义为：若第行属于第个聚簇，说明属于第个聚簇。

,

,

…,

步骤7 构建模糊关系矩阵。由引言可知，影响模糊时间序列预测准确性的核心内容除了论域划分外，还包括模糊关系的提取。对于时间序列而言，各时刻的预测值往往是不确定的，而传统的模糊逻辑关系表示往往忽略了这一点。

若将模糊集视为状态，模糊关系即为状态间的转移关系，即可利用高阶Markov概率模型表示上述高阶模糊逻辑关系，方便考虑之前时刻的数据影响后续数据的各种可能性；并将其描述为矩阵的形式，从而可以利用矩阵分析方法对其进行分析以获得时间序列的整体特性。构建的二阶模糊关系矩阵如式(4)所示。

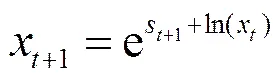
4 实验分析

本文在真实以及人工数据集上进行实验，并通过与当前2种主流时间序列预测方法：自回归和基于神经网络的预测方法，以及3种模糊时间预测方法：平均划分论域、基于-means和层次聚类的论域划分方法的预测结果进行对比，说明所提模糊时间序列预测方法能够获得相对较准确的预测效果。

为了分析预测效果，选取2种常用的度量时间序列预测准确性的指标：预测误差方差（MSE, mean square error）和泰尔不等系数（TIC, Theil inequality coefficient）[32]

4.1 真实数据集

随着通信技术的发展，通话行为的方式发生了较大变化，人们由较早的以手机通话为主的业务模式转变为以数据为主的业务模式，由于数据业务可支撑的应用极多，较难从中分析通话模式，因此本文选择相对较早的纯通话业务数据，进行通话行为模式的分析。同时选用粒度过细的长期数据样本构建预测模型会使模型极不稳定，导致预测结果误差增大[33]。那么以中国某省会城市2004年~2009年各月的电信话务量真实时间序列数据作为验证所提模型有效性的实验数据集，并选取其中2004年1月~2009年5月的数据作为训练样本数据集，2009年6月~2009年12月的数据则作为测试数据集。预测目的是希望基于历史话务量数据，对未来的话务量进行预测。该时间序列数据的原始分布如图1(a)所示，按式(1)计算的原始数据所对应的趋势值分布情况如图1(b)所示。可见趋势转化后的数据分布特点相较于原始数据而言分布特征更明显。

如图2所示，趋势转化后的数据也在一定程度上出现了相关性，因此本文所提模型将以趋势转化后的数据作为预测的基础，并且在获得话务量趋势数据后，利用高斯相关函数构建相似矩阵，相似矩阵的数值分布如图3所示。根据谱聚类特征值计算方法求得特征值序列，在图4所示的特征值序列中，在第6、12、20个特征值处，特征值的差值有明显地变化，且在数值上呈现递增。因此选取前6个、前12个以及前20个特征向量作为特征向量子空间，分别对趋势数据进行拟合，拟合效果如图5所示，通过比较3个特征值可知，模型拟合的效果随着特征向量的增加而提高，且在特征向量为20时最好，但相对于12个特征向量时，模型拟合效果提升不大，且容易出现过拟合影响适应能力。

图6所示的各典型预测方法的拟合曲线对比也显示了相较于其他预测方法，本文所提模型SFTP得到的值更加接近于原始数据，适应性更强，具有更好的拟合效果。

此外，进一步对几种预测方法关于2种预测指标MSE与TIC的结果进行对比，如图7所示，其中MSE值为利用小数定标规范化后的结果。可以发现所提SFTP算法相较于其他算法，能够取得较低的评价指标值，即可以获得较好的预测效果。主要是相较于普通的时间序列预测方法， SFTP利用了模糊时间序列建模方法，充分考虑了数据的原始特征；而相较于几种对比的模糊时间序列预测方法，基于谱聚类进行论域划分并不需要预先对数据的分布进行假设，并且它基于数据间的相似矩阵，将聚类问题转换为对矩阵的谱分解问题，如前所述，模糊时间序列数据之间具有一定的关联关系，因此基于谱聚类的方法能够较准确地获取数据的分布情况，从而有助于论域划分；另外，基于高阶Markov概率模型描述模糊时间序列中的高阶模糊关系的方法，也充分考虑了时间序列中历史数据对未来数据产生的各种可能的影响。可见本文所提模型在论域划分以及模糊关系提取这2个影响模糊时间序列预测准确性的核心内容上，均提供了有效的解决方法。

4.2 人工数据集

为了进一步验证所提算法的有效性，本文还选取了4个常见的人工时间序列数据集[33]：Stock、Room Nights、Male Incidence和Sale，进行对比实验。如图8所示为几种预测算法在该4个数据集上关于2种预测指标MSE与TIC的对比结果，同样的，其中MSE值为利用小数定标规范化后的结果。其中在Stock与Room Nights数据集上，SFTP与AR算法均获得了较低的MSE和TIC值，即预测结果较准确；而在另2个数据集上，相较于几种对比算法，SFTP也均能表现出较准确的预测效果。这主要是因为SFTP利用数据原始特征，无需对数据分布进行预先假设，基于谱聚类可较准确地获取数据的分布情况；同时充分考虑了时间序列中历史数据对未来数据产生的各种可能的影响。而AR在几个数据集上也能获得较好的预测效果，说明简单的预测模型在简单的时间序列数据中即能发挥较准确的预测作用。

通过上述分析可知，在几种典型时间序列人工数据集上的实验结果也进一步验证了所提SFTP算法的有效性。

5 结束语

针对模糊时间序列预测方法中存在的问题，本文提出一种基于谱聚类的模糊时间序列预测方法。该模型基于谱聚类进行论域划分，在不对数据分布进行预先假设的基础上，能够有效地划分原时间序列数据的论域；另外模型利用高阶Markov概率模型描述模糊时间序列中的高阶模糊关系，并据此对后续数据进行预测，使之前时刻的数据对后续数据产生的各种可能影响均被处理。即从论域划分以及模糊关系提取2个方面保证了模型预测的准确性。在真实时间序列数据集上的实验表明了所提预测方法的有效性。

[1] SONG Q, CHISSOM B S. Fuzzy time series and its models [J]. Fuzzy Sets System, 1993, 54(3): 269-277.

[2] SONG Q, CHISSOM B S. Forecasting enrollments with fuzzy time series [J]. Part I Fuzzy Sets System, 1993, 54(1): 1-9.

[3] SONG Q, CHISSOM B S. Forecasting enrollments with fuzzy time series [J]. Part II Fuzzy Sets System, 1994, 62(1): 1-8.

[4] LEE L W, WANG L H, CHEN S M. Temperature prediction and TAIEX forecasting based on high-order fuzzy logical relationships and genetic simulated annealing techniques [J]. Expert Systems with Applications, 2008, (34): 328-336.

[5] CHEN S M, HWANG J R. Temperature prediction using fuzzy time series [J]. IEEE Transactions on Systems, Man, Cybernetics-Part B: Cybernetics, 2000, 30(2): 263-275.

[6] 王兆霞,孙雨耕. 基于模糊神经网络的网络业务量预测研究[J]. 通信学报, 2005,26(3):136-140.

WANG Z X, SUN Y G. Study of predicting network traffic using fuzzy neural networks[J].Journal on Communications, 2005,26(3):136-140.

[7] YU H K. Weighted fuzzy time-series models for TAIEX forecasting [J]. Physical A, 2004, (349): 609-624.

[8] 张韬, 冯子健. 模糊时间序列分析在肾综合征出血热发病率预测的应用初探[J]. 中国卫生统计, 2011, 2:146-150.

ZHANG T, FENG Z J. Application of fuzzy time series analysis in incidence of hemorrhagic fever with renal syndrome prediction [J].China Health Statistics, 2011, 2:146-150.

[9] 倪明. 模糊时间序列预测模型研究及其在污水处理上的应用[D]. 西南石油大学,2012.

NI M. Fuzzy time series forecasting model and its application in wastewater treatment[D]. Southwest Pe troleum University, 2012.

[10] ALADAG C H, EGRIOGLU E. A high order seasonal fuzzy time series model and application to international tourism demand of turkey[J]. Applications in Engineering and Technology, 2014, 26(1):295-302.

[11] HUARNG K. Effective lengths of intervals to improve forecasting in fuzzy time series[J]. Fuzzy Sets and Systems, 2001, 123(3): 387-394.

[12] LI S T, CHEN Y P. Natural partition-based forecasting model for fuzzy time series[C]//The IEEE International Conference on Fuzzy Systems Budapest. Hungary, c2004:25-29.

[13] CHEN S M, HSU C C. A new method to forecast enrollments using fuzzy time series [J]. International Journal of Applied Science and Engineering, 2004, 2(3): 234-244.

[14] TRAN T N, WEHRENS R, BUYDENS L. KNN-kernel density-based clustering for high-dimensional multivariate data [J]. Computational Statistics and Data Analysis, 2006, 51(2): 513-525.

[15] CHENG C H, CHANG J R, YEH C A. Entropy-based and trapezoid fuzzification-based fuzzy time series approaches for forecasting IT project cost [J]. Technological Forecasting and Social Change, 2006, 73(5): 524-542.

[16] HUARNG K, YU T H. Ratio-based lengths of intervals to improve fuzzy time series forecasting [J]. IEEE Transactions on Systems,Man, and Cybernetics-Part B: Cybernetics, 2006, 36(2): 328-340.

[17] LEE L W, WANG L H, CHEN S M. Temperature prediction and TAIFEX forecasting based on fuzzy logical relationships and genetic algorithms [J]. Expert Systems with Applications, 2007, (33): 539-550.

[18] CHENG C H, CHENG G W, WANG J W. Multi-attribute fuzzy time series method based on fuzzy clustering [J]. Expert Systems with Applications, 2008, 34(2): 1235-1242.

[19] YOLCU U, EGRIOGLU E, USLU V R. A new approach for determining the length of intervals for fuzzy time series [J]. Applied Soft Computing, 2009, 9(2): 647-651.

[20] EGRIOGLU E, ALADAG C H. Fuzzy time series forecasting with a novel hybrid approach combining fuzzy c-means and neural networks[J]. Expert Systems with Application, 2013, 40(3):854-857

[21] KHASHEI M. Fuzzy artificial neural network p, d, q model for incomplete financial time series forecasting[J]. Applications in Engineering and Technology, 2014, 26(2):831-845.

[22] CHEN S M, KAO P Y. TAIEX forecasting based on fuzzy time series, particle swarm optimization techniques and support vector machines[J]. Information Sciences, 2013, 247(15):62-71.

[23] BAS E, USLU V R, YOLCU U. A modified genetic algorithm for forecasting fuzzy time series[J]. Applied Intelligence, 2014, 41(2): 453-463.

[24] 曹盼盼, 阎春宁. 人类通信模式的幂律分布和Zipf定律[J]. 复杂系统与复杂科学, 2009, 6(4):51-56.

CAO P P, YAN C N. The power law and Zipf’s law in human communication patterns [J]. Complex Systems and Complexity Science, 2009, 6(4):51-56.

[25] CHEN S M, WANG N Y, PAN J S. Forecasting enrollments using automatic clustering techniques and fuzzy logical relationship [J]. Expert Systems with Applications, 2009, 36(8): 11070-11076.

[26] CHEN S M, TANUWIJAYA K. Multivariate fuzzy forecasting based on fuzzy time series and automatic clustering techniques [J]. Expert Systems with Applications, 2011, 38(8):10594-10605.

[27] MILLS T C. Time series techniques for economists[M]. Cambridge: Cambridge University Press, 1990.

[28] LI S T, KUO S C, CHENG Y C, et al. A vector forecasting model for fuzzy time series [J]. Applied Soft Computing, 2011, 11(3): 3125-3134.

[29] WANG W, LIU X. Fuzzy forecasting based on automatic clustering and axiomatic fuzzy set classification [J]. Information Sciences, 2015, 294(294): 78-94.

[30] NG A Y, JORDAN M I, WEISS Y. On spectral clustering: analysis and an algorithm [J]. Advances in Neural Information Processing Systems, 2002, 2(8):849-856.

[31] LUXBURG U V. A tutorial on spectral clustering [J]. Statistics and Computing, 2007, 17(4):395-416.

[32] LI M, LI Y C, LENG J X. Powertype functions of prediction error of sea le-vel time series[J]. Entropy, 2015, 17(7): 4809-4837.

[33] LI M, LI J Y. On the predictability of long-range dependent series[J/OL]. Mathematical Problems in Engineering, 2010, article ID 397454. http://datamarket.com/data/

High-order fuzzy time series self-adaption prediction method based on spectral clustering

ZHOU Chun-nan, HUANG Shao-bin, CHI Rong-hua, LI Ya, LANG Da-peng

(College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, China)

A fuzzy time series self-adaption prediction method based on spectral clustering and data characteristics was proposed. First, based on spectral clustering and the characteristics of data, the number and scope of the discourses was obtained to convert into fuzzy time series self- adaptively. Then, fuzzy relationships based on Markov probability model was presented, and the multi-steps, high-order and steady fuzzy relationship are gotten. Finally, proposed meted obtained the probable fuzzy states, and got its predicted values based on defuzzification methods. Experiments on real-world and synthetic time series data indicate the rationality and effectiveness of the proposed method.

fuzzy time series, spectral clustering, discourse partition, Markov probability model, fuzzy relationship

TP399

A

10.11959/j.issn.1000-436x.2016036

2015-05-11；

2015-09-16

中央高校基本科研业务专项基金资助项目（No.HEUCF100603, No.HEUCFZ1212）

The Fundamental Research Funds for the Central Universities (No.HEUCF100603, No.HEUCFZ1212)

周春楠（1971-），男，黑龙江哈尔滨人，哈尔滨工程大学博士生，主要研究方向为时间序列预测、数据挖掘、不确定性研究等。

黄少滨（1965-），男，黑龙江哈尔滨人，哈尔滨工程大学教授、博士生导师，主要研究方向为分布式计算与仿真、模型检测、数据集成等。

迟荣华（1981-），男，黑龙江哈尔滨人，哈尔滨工程大学博士生，主要研究方向为复杂网络、不确定性研究等。

李雅（1985-），女，黑龙江哈尔滨人，哈尔滨工程大学博士生，主要研究方向为模型监测等。

郎大鹏（1983-），男，黑龙江哈尔滨人，哈尔滨工程大学博士生，主要研究方向为模型监测等。