基于平均概率和停止准则的多元LDPC码加权符号翻转译码算法

郭锐，刘春于，王美洁，潘鹏，包建荣,2，郭春生



基于平均概率和停止准则的多元LDPC码加权符号翻转译码算法

郭锐1，刘春于1，王美洁1，潘鹏1，包建荣1,2，郭春生1

（1. 杭州电子科技大学通信工程学院，浙江杭州 310018；2. 东南大学移动通信国家重点实验室，江苏南京 210096）

为了提高多元低密度奇偶校验(LDPC, low density parity-check)码符号翻转译码算法的性能并降低译码的复杂度，提出了基于平均概率和停止准则的多元LDPC码加权符号翻转译码(APSCWSF, average probability and stopping criterion weighted symbol flipping)算法。该算法将校验节点邻接符号节点的平均概率信息作为权重，使翻转函数更加有效，提高符号的翻转效率，进而改善译码性能。并且通过设置迭代停止准则进一步加快算法的收敛速度。仿真结果显示，在加性高斯白噪声信道下，误符号率为10−5时，相比WSF算法、NSCWSF算法(=10)和NSCWSF算法(=6)，APSCWSF算法(=10)分别获得约0.68 dB、0.83 dB和0.96 dB的增益。同时，APSCWSF算法(=6)的平均迭代次数也分别降低78.60% ~79.32%、74.89% ~ 75.95% 和67.20% ~70.80%。

多元低密度奇偶校验码；加权符号翻转译码；平均概率；停止准则；翻转函数

1 引言

相比二元LDPC码，多元LDPC码具有更强的抗突发错误能力，但译码的复杂度相对较高，因而寻找译码性能好且复杂度相对较低的译码算法显得尤为重要[1,2]。多元LDPC软判决译码算法主要有GF()上的置信传播(BP, belief propagation)译码算法[3]、基于快速傅里叶变换的置信传播(FFT-BP, fast Fourier transform belief propagation)译码算法、最大置信传播算法(MAX-LOG-BP)及扩展最小和(EMS, extended min-sum)译码算法[4,5]。这些软判决译码算法虽然具有较好的译码性能，但译码迭代过程中涉及到的实数运算量较大，不利于硬件实现。多元LDPC硬判决译码算法主要是符号翻转(SF, symbol flipping)译码算法，该算法实现简单，因此比较适用于一些对译码速度要求较高的场合。在SF算法的基础上进行改进，形成WSF(weighted symbol flipping)算法[6~8]。该算法通过引入不同的可靠性度量值进而改善SF算法的译码性能。此后，又提出了基于新停止准则的WSF(NSCWSF, new stopping criterion weighted symbol flipping)算法[9,10]和多样投票的符号翻转(MV-SF, multiple-vote symbol flipping)算法[11]。

为了提高多元LDPC码符号翻转译码算法的译码性能并加快译码的速度，本文提出了基于平均概率和停止准则的多元LDPC码加权符号翻转译码(APSCWSF, average probability and stopping criterion weighted symbol flipping)算法。该算法将与校验节点邻接符号节点的平均概率信息作为权重，得到更加有效的可靠度软信息，提高符号的翻转效率，从而改善算法的译码性能并加快算法的收敛速度。与此同时，通过增加控制迭代次数的迭代停止准则进一步加快译码的收敛速度，进而降低译码的复杂度。

2 多元LDPC码符号翻转译码算法

多元LDPC码与二元LDPC码类似，可以用稀疏检验矩阵来描述，是校验矩阵的行数，每行代表一个校验方程，是校验矩阵的列数，每列则代表一个编码码字。对于()码，必须不小于。校验矩阵中的每个元素H都必须取值于有限域GF(=2)。校验矩阵中每行、每列中非零元素个数分别相等，称为规则码，反之称为非规则码。对于规则多元LDPC码，稀疏检验矩阵的行重记为d，列重记为d。与第个校验方程邻接的d个符号节点集合记为()，与第个符号节点相关联的d个校验方程记为()。对于任意一个长度为的向量如果满足T=0,则称向量是一个合法的码字。假设=[01x−1]为任一输入信息序列，其中中的每个元素x都取值于有限域GF(=2)，的长度为。经编码后的码字=[01c−1]GF(=2),采用BPSK调制方式，经过加性高斯白噪声(AWGN, additive white Gaussian noise)信道输出=[01r−1]。

2.1 符号翻转译码算法

SF算法是一种硬判决译码算法。首先，对信道输出的二进制序列序列进行硬判决，得到硬判决序列=[01b-1]。判决规则如下：若r≥0，将b判决为1；若r﹤0，则将b判决为0()。因为硬判决得到的是一个二进制序列，所以要根据二进制和进制的转换原则，将长度为的二进制序列转换成一个长度为的进制序列=[01y−1]，定义映射：,y=([b（+1）−1])()。这里得到的序列=[01y−1]就是SF算法的输出序列[12,13]。

2.2 加权符号翻转译码算法

为了改善SF算法的译码性能，在SF算法的基础上，WSF算法增加适量的可靠度软信息作为权重。硬判决后，WSF算法需要计算符号的初始化似然概率，为后面译码迭代过程中计算与校验方程邻接所有符号节点的平均似然概率做准备。定义GF0() ={}为除零元素之外的有限域，则符号概率对数似然比如式(1)所示。

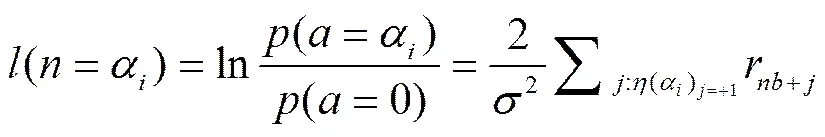
(2)

WSF算法是一种基于可靠度软信息的SF算法。为了确定要翻转符号的位置，首先计算每一个符号节点分别取每一个GF0()中元素的度量值，最后通过求和的方式得到每一个符号节点的可靠性度量值[15]，如式(3)所示。

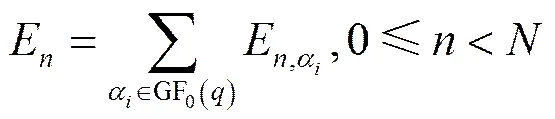
3 基于平均概率的加权符号翻转译码算法

3.1 APWSF算法描述

WSF算法只是将与校验节点邻接的符号节点（除去待翻转符号节点）的最小概率作为权重，而忽略了大量符号节点的可靠度软信息[16,17]，因此WSF算法的性能并不理想。为了使翻转函数获得更加准确的可靠性软信息，提高符号的翻转效率，从而改善算法的译码性能，本文提出了基于平均概率的加权符号翻转译码(APWSF, average probability weighted symbol-flipping)算法。该算法将与校验方程邻接符号节点的平均概率信息作为权重，从而把校验方程邻接的所有符号节点的可靠度软信息都考虑在内，同时引入加权因子，将信道直接提供给待翻转符号节点自身的可靠度软信息进行加权。

APWSF算法的具体流程如下。

步骤1 初始化参数，将迭代次数初始化为零，设置最大迭代次数max和加权因子。将排除符号序列初始化为空，比特翻转标识flip初始化为1。其中排除符号序列是用来存储那些不满足翻转条件的符号所对应的位置；比特翻转标识flip作为一个计数器使用，它的最大可取值为，即lb。flip的值决定待翻转符号中需要翻转比特的个数。

步骤2 计算初始硬判决输出序列，并将该序列作为=0时译码迭代的输出，记为(0)。

步骤3 获取与校验方程邻接所有符号节点的平均概率信息。首先利用式(1)计算概率矩阵=[]()，进而计算平均概率矩阵[]，其中。是一个行、1列的概率矩阵，表示与第个校验方程相邻接的所有符号节点取符号的平均概率信息，的计算式为

(4)

其中，d表示与第个校验方程邻接的符号节点的个数。

步骤4 计算伴随向量(k)，(k)=(k)T。若伴随向量(k)=0，则停止译码迭代，将此时的(k)和迭代次数输出；若伴随向量(k)≠0，且此时等于最大迭代次数max, 表明译码失败，停止译码迭代，输出此时的(k)和迭代次数；否则将迭代次数自动加1，进行下一次迭代。

步骤5 计算第次迭代时每一个符号节点的可靠度量值()。为了计算则首先需要计算符号节点分别取{} ()的可靠度量值

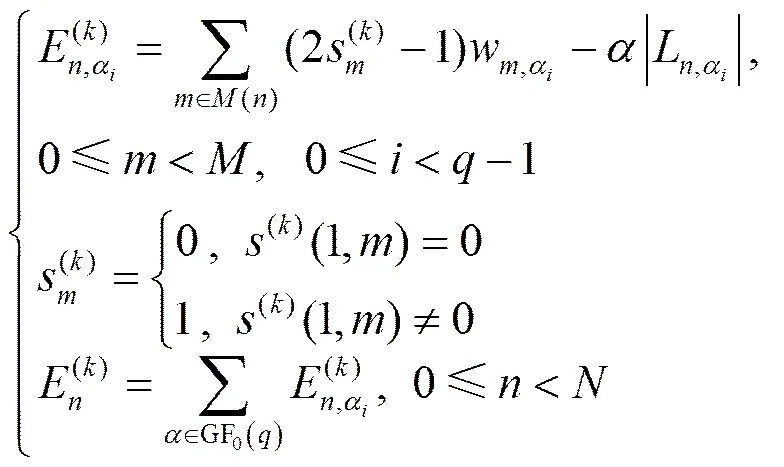
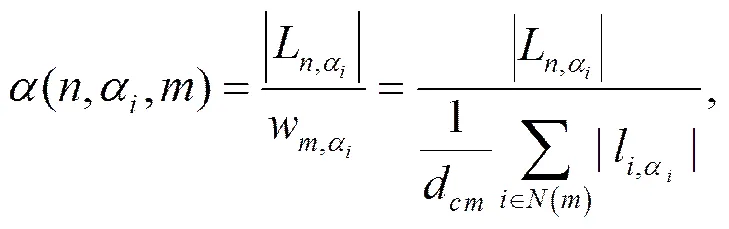
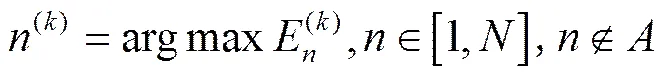
步骤7 确定待翻转符号需要翻转的幅度大小。符号位置中具体要翻转的比特位置是由经过AWGN信道传输后输出的二进制序列[01r−1]所决定。待翻转符号位置处的符号可以转换成个比特，这个比特与中的[rr+1(n+1)b−1]相对应。将|r|()进行从大到小排序，|r|越小，则对应比特的可靠性越低。因此根据比特翻转标识flip选取[r(n+1)b−1]中绝对值最小的flip个比特位置，并翻转对应位置的flip个比特，从而得到新符号序列(k)=[01y−1]。

步骤8 检测是否存在死循环。死循环的检测方法如下，首先定义输出符号序列矩阵(k+1)×N，如式(8)所示。

=(8)

接着定义一个死循环检测矩阵，如式(9)所示。

=(9)

只要死循环检测矩阵中存在一行元素全部为零，称检测到死循环。否则没有检测到死循环。

1) 如果检测到死循环且flip并未达到其最大值，将flip加1，然后返回到步骤7重新确定翻转符号要翻转的具体比特位置，并翻转对应位置的flip个比特。

2) 如果检测到死循环但flip已达到其最大值，将当前所选择的翻转符号位置存储到排除符号序列中，并将比特翻转标识flip置1。然后返回到步骤6重新寻找翻转符号的位置。

3) 如果没有检测到死循环，则将排除符号序列设置为空，比特翻转标识flip置1，返回步骤4。

3.2 对APWSF算法的改进

APWSF算法与WSF算法相比，在译码性能和译码速度方面都得到了很大程度的提高。为了进一步加快译码的收敛速度，对本文提出的APWSF算法做进一步的改进，称之为APSCWSF算法。该算法是在APWSF算法的基础上，通过增加控制迭代次数的迭代停止准则得到。

为了阐述APSCWSF算法，首先定义“可正确译码的码字”和“不可正确译码的码字”。所谓“可正确译码的码字”是指那些随着迭代次数的增加，不满足校验方程的个数迅速减少，即伴随向量(k)中的非零元素个数迅速减少的那些码字；而“不可正确译码的码字”是指那些随着迭代次数的增加，不满足校验方程的个数没有呈现明显减少趋势，而出现了反复振荡的那些码字。

迭代停止准则具体描述如下。

首先，定义检测反复振荡期的下限为1，上限为2；定义振荡计数器Count并赋初值0, Count的最大值为；定义检测窗口向量()，窗口的长度为l。其中，和l值可以先选取，再通过数据仿真检验调整[10]。计算第+1次迭代后不满足校验方程的个数(+1)，并与第次迭代后不满足校验方程的个数()作差得到差值()，如式(10)所示。

()=(+1)−() (10)

然后令检测窗口向量()=[()(+1)(+l−1)]，当迭代次数达到该窗口长度l的整数倍时，开始对检测窗口向量()的每一个元素(+)进行检测。如果对于检测窗口内的每一个元素(+)都满足，则说明不满足校验方程的个数处于振荡期，将振荡计数器Count加1。当振荡计数器Count达到它的最大值时，就认为该码字是不可正确译码的，提前停止译码迭代并输出此时的(k)和迭代次数。

3.3 复杂度理论分析

本节对复杂度进行定性分析，在4.2节中将对复杂度进行具体的定量分析，并详细比较各个算法所需的加法运算平均总次数。表1分别给出了WSF译码算法、NSCWSF译码算法、MV-SF译码算法以及本文提出的APWSF译码算法和APSCWSF译码算法所需的运算复杂度，其中A指各个算法所需的迭代次数，表示校验矩阵的行数，表示校验矩阵的列数，代表校验矩阵的行重，代表校验矩阵的列重。其中对于MV-SF译码算法，表示测试向量的长度，作为协调译码复杂度和译码性能的参数。

由表1可得如下结论。

1) APWSF算法的复杂度低于WSF算法。WSF算法和APWSF算法每次迭代的计算量相同，差别仅在于迭代次数。但APWSF算法的迭代次数要远小于WSF译码算法。

2) NSCWSF算法的复杂度低于WSF算法。虽然NSCWSF算法每次迭代所需的加法运算总次数(多出迭代停止准则的部分—)稍大于WSF算法，但是NSCWSF译码算法的迭代次数远小于WSF算法。MV-SF算法不仅需要大量加法运算，而且需要乘法运算。

3) APSCWSF算法的复杂度低于APWSF算法。APSCWSF算法每次迭代所需的加法运算总次数(多出迭代停止准则的部分—)稍大于APWSF算法，但APSCWSF算法的迭代次数远少于APWSF算法。

表1 5种不同译码算法实数运算的复杂度

4 性能仿真与分析

4.1 仿真参数设置

仿真所采用的码字具体参数如下。

1) GF(=24)的QC LDPC码[18](999,888)(简称码A)，码A的码率为，行重为27，列重为3。在码A的系统仿真中，将译码的最大迭代次数max设置为100次；对于NSCWSF算法和APSCWSF算法，检测窗口的长度l设置为10。2) GF(=26)的QC LDPC码(999,888)(简称码B)，码B的码率为，行重为27，列重为3。对码B的系统仿真中，将译码的最大迭代次数max设置为100次；对于NSCWSF算法和APSCWSF算法，检测窗口的长度l设置为10。3) GF(=26)的LDPC码(142,71)(简称码C)，码C的码率为，行重为4，列重为2。对码C的系统仿真中，将译码的最大迭代次数max设置为50次，对于NSCWSF算法和APSCWSF算法，检测窗口的长度l设置为4。4) GF(=25)的LDPC码(834,723)(简称码D)，码D的码率约为0.867，行重为27，列重为2。对码D的系统仿真中，将译码的最大迭代次数max设置为10次，对于NSCWSF算法和APSCWSF算法，检测窗口的长度l设置为2。5) GF(=25)的LDPC码(1455,1344)(简称码E)，码E的码率约为0.923，行重为27，列重为3。在码E的系统仿真中，将译码的最大迭代次数max设置为10次，对于NSCWSF算法和APSCWSF算法，检测窗口的长度l设置为2。

4.2 译码性能仿真与结果分析比较

本节主要对文献[7]中提出的WSF算法、文献[10]中提出的NSCWSF算法(=3、=6、=10)、文献[11]中提出的MV-SF算法，以及本文提出的APWSF算法和APSCWSF算法(=3、=6、=10)进行系统仿真，并对各个译码算法的误符号率(SER, symbol-error rate)、误帧率(FER, frame-error rate)和平均迭代次数这3个参数指标进行比较。其中，码A、码B、码C主要对WSF算法、NSCWSF算法、APWSF算法、APSCWSF算法进行系统仿真，误符号率曲线、误帧率曲线、平均迭代次数曲线分别如图1~图9所示。利用码D、码E对MV-SF算法、WSF算法、NSCWSF算法、APWSF算法、APSCWSF算法的误帧率进行了仿真，分别如图10、图11所示。

由仿真图可知，本文提出的新算法(APWSF算法和APSCWSF算法(=6,10))性能明显优于已有的WSF算法、NSCWSF(=6,10)算法和MV-SF算法。随着振荡计数器最大值的增大，带有停止准则的NSCWSF算法和APSCWSF算法的性能将分别越接近于WSF算法和APWSF算法。在信噪比较低时，NSCWSF算法和APSCWSF算法的性能分别略优于WSF算法和APWSF算法。因为在信噪比较低时，存在较多的“不可正确译码码字”，设置停止准则提前终止迭代反而会减少译码中错误的码字个数。由图3、图6、图9可知，在相同信噪比情况下，本文提出的新算法(APWSF算法和APSCWSF算法(=6,10))所需的平均迭代次数远少于已有的WSF算法和NSCWSF(=6,10)算法，其中APSCWSF算法(=6)在所有的算法中平均迭代次数最少。

表2给出了码A、码B、码C的误符号率为10−5时，本文提出的新算法相对于其他已有算法获得的增益。由表2可知，对于码A、码B、码C，在误符号率为10−5时，APWSF算法的性能是最好的，APSCWSF算法(=10)次之，NSCWSF算法(=6)最差。与WSF算法相比，本文提出的APSCWSF算法(=10)分别获得约0.72 dB、0.68 dB和0.42 dB的增益；与NSCWSF算法(=10)相比，分别获得约0.75 dB、0.83 dB和0.44 dB的增益；与NSCWSF算法(=6)相比，分别获得约0.83 dB、0.96 dB和0.50 dB的增益。

表3给出了码D、码E的误帧率为10−3时，本文提出的新算法相对于其他已有算法获得的增益。由表3可知，对于码D，相比MV-SF(=2,=6)算法，本文提出的APSCWSF算法(=3)分别获得约1.00 dB和0.95 dB的增益；相比 NSCWSF算法(=3)，获得约0.83 dB的增益；相比WSF算法(=3)，获得约0.75dB的增益；对于码E，相比MV-SF(=2,=6)算法，本文提出的APSCWSF算法(=3)分别获得约1.05 dB和1.00 dB的增益；相比 NSCWSF算法(=3)，获得约0.80 dB的增益；相比WSF算法(=3)，获得约0.70 dB的增益。

表4、表5分别给出了在码A情况下，各种译码算法的平均迭代次数和加法运算总次数。由表4统计可得，码A在2 dB和3 dB时，相对于WSF算法、NSCWSF算法(=10)和 NSCWSF算法(=6)，APSCWSF算法(=6)平均迭代次数分别降低60.66% ~79.32%、49.26%~75.95%和33.81%~ 70.80%。由表5统计可得，码A在2 dB和3 dB时,相比于其他算法，APSCWSF算法的译码复杂度最低，APSCWSF算法(=6)的平均加法运算总次数降低67.20%~79.32%。因此，与已有的WSF算法和NSCWSF算法相比，APSCWSF算法不但提高了译码性能，而且极大地减少了译码的迭代次数。

改善性能的主要因素为，构造翻转函数时，将校验方程邻接的符号节点的平均概率信息作为权重，获得了更加可靠的翻转信息，从而译码迭代过程中得到的待翻转符号更加精确。WSF算法和NSCWSF算法中，只是将校验方程邻接的符号节点的最小概率信息作为权重，MV-SF算法只是考虑了部分符号节点的概率信息，都忽略了大量信息节点的可靠度信息。迭代次数降低的主要因素有两方面，一方面仍然由于将校验方程邻接的符号节点的平均概率信息作为权重，翻转函数获得了更加可靠的信息，从而加速了译码迭代的收敛；另一方面，增加控制译码迭代次数的停止准则，从而大大减少了“不可正确译码码字”的翻转次数。

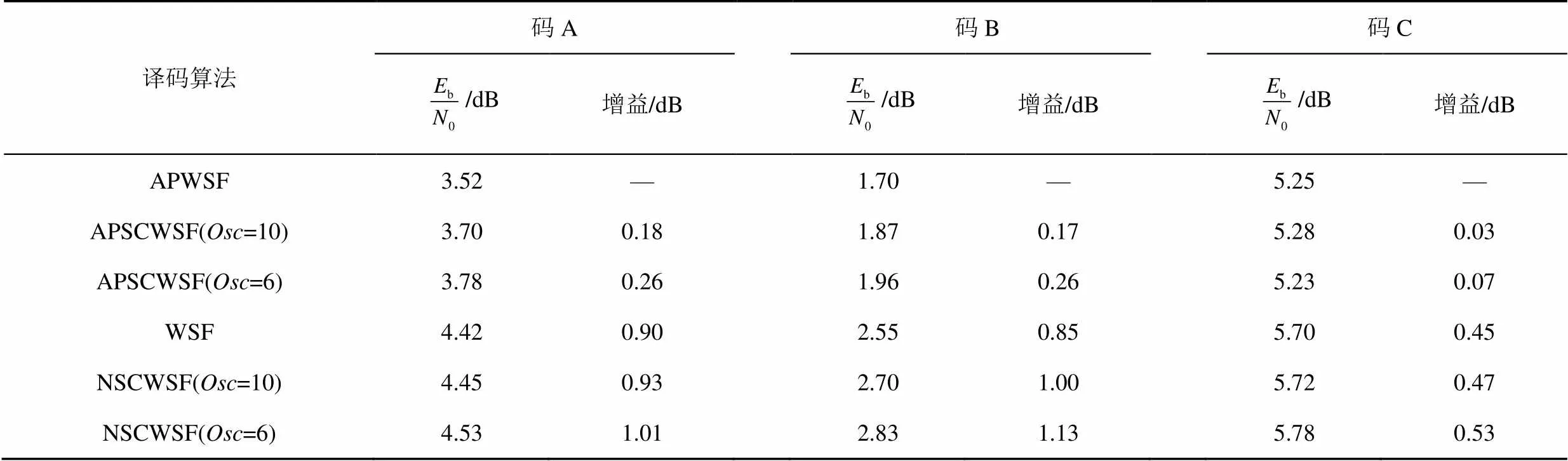
表2 SER=10−5时，相比已有的算法，本文提出的新算法获得的增益统计

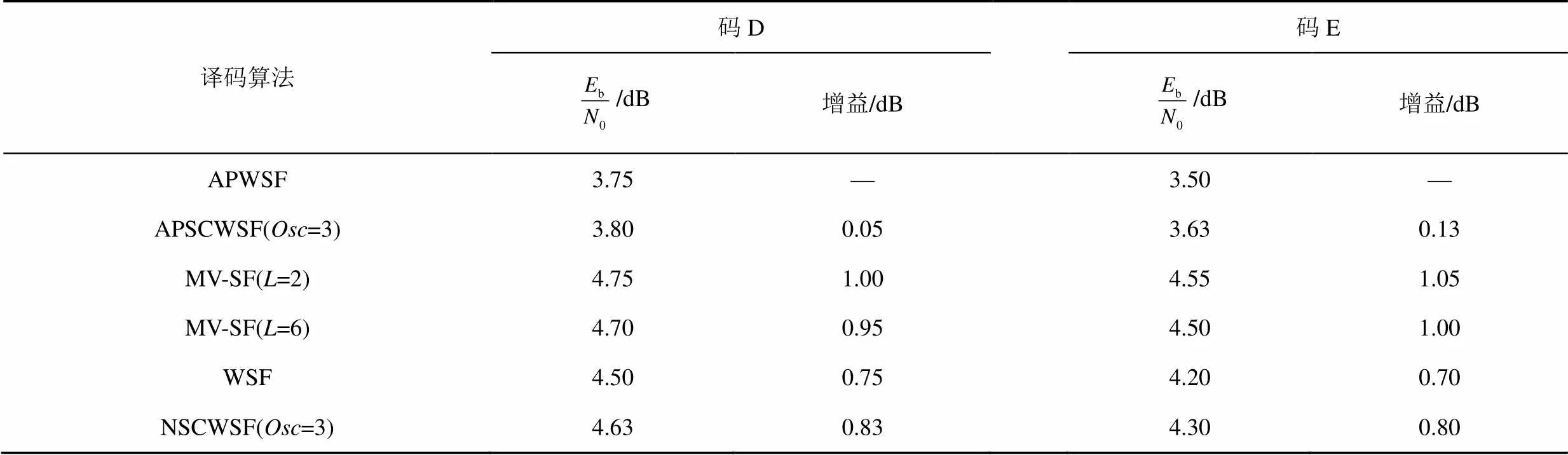
表3 FER=10−3时，相比已有的算法，本文提出的新算法获得的增益统计

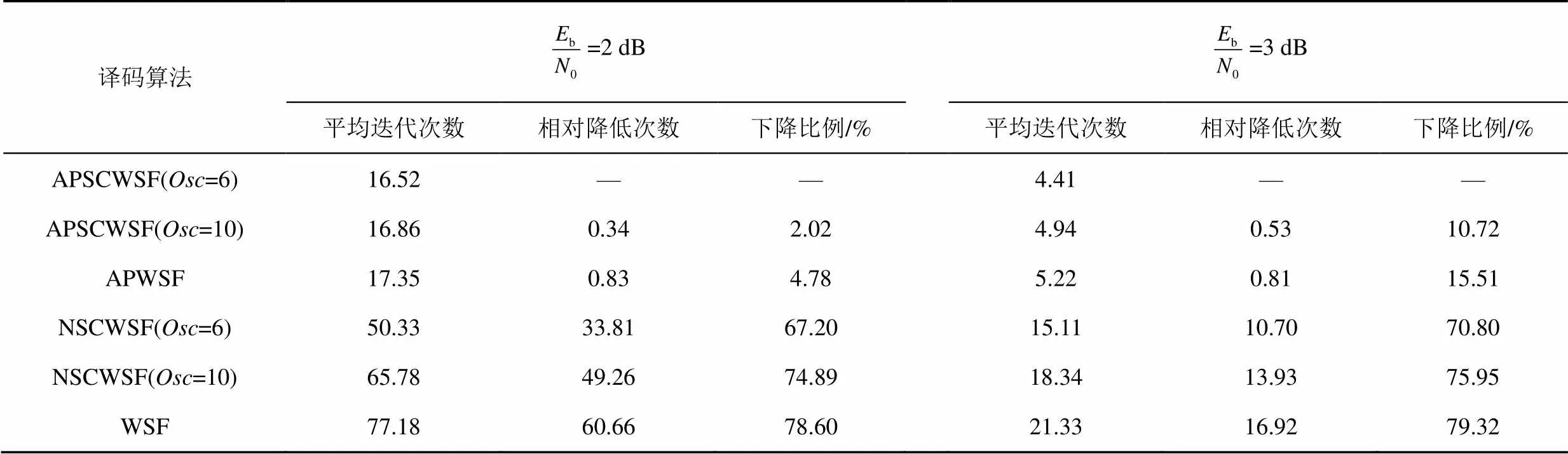
表4 码A在2 dB和3 dB时，APSCWSF算法(Osc=6, Osc=10)和其他算法的迭代次数比较

表5 码A在2 dB和3 dB时，各种译码算法所需的译码复杂度

5 结束语

本文提出了基于平均概率和停止准则的多元LDPC码加权符号翻转译码(APSCWSF)算法。该算法将校验节点邻接的符号节点的平均概率信息作为权重，得到更加有效的翻转函数，提高了符号的翻转效率，从而改善算法的译码性能，并通过增加迭代停止准则来进一步加快译码的收敛速度。仿真结果表明，与已有的WSF算法、NSCWSF算法和MV-SF算法相比，本文提出的APSCWSF算法可分别获得约0.75 dB、0.83 dB和1.00 dB的增益；相比WSF算法、NSCWSF算法，APSCWSF算法的加法运算的平均总次数分别降低76.58%~79.14%和67.17% ~70.81%。由此可见，本文提出的APSCWSF算法获得了性能和复杂度之间更好的匹配，可以更好地满足高速通信系统对译码算法的需求。

[1] PENG R, CHEN R. Design of nonbinary LDPC codes over() for multiple-antenna transmission[C]//IEEE Military Communications Conference. Washington, DC, USA, c2006:1-7.

[3] TENG M, LIU X, DENG Z. Improved BP decoding algorithm for nonbinary LDPC codes based on bit-flipping method[C]//International Conference on Computational Intelligence and Security. Suzhou, China, c2008:376-380.

[4] GUO X, FEI Y. Adaptive extended min-sum algorithm for nonbinary LDPC decoding[C]//IEEE Global Telecommunications Conference Houston, TX, USA, c2011:1-6.

[5] ZHAO S, LU Z, MA X, et al. A variant of the EMS decoding algorithm for nonbinary LDPC codes[J]. IEEE Communications Letters, 2013, 17(8): 1640-1643.

[6] LIU B, GAO J, DOU G. Majority decision based weighted symbol-flipping decoding for nonbinary LDPC codes[C]//The 2010 2nd International Conference on Future Computer and Communication. Wuhan, China, c2010: 223-226.

[7] LIU B, DOU G, TAO W, et al. Weighted symbol-flipping decoding for nonbinary LDPC codes[C]//The 2010 2nd International Conference on Networks Security, Wireless Communications and Trusted Computing. Wuhan, China, c2010: 223-226.

[8] LIU B, DOU G, TAO W, et al. Efficient stopping criterion for hybrid weighted symbol-flipping decoding of nonbinary LDPC codes[J]. IEEE Communications Letters, 2011, 15(3): 337-339.

[9] CHEN X, MEN A, ZHOU W. A stopping criterion for nonbinary LDPC codes over GF()[C]//The 2008 11th IEEE Singapore International Conference on Communication Systems. Guangzhou, China, c2008: 1312-1315.

[10] 刘冰, 陶伟, 窦高奇, 等. 基于新停止准则的多进制LDPC码加权符号翻转译码算法[J]. 电子与信息学报, 2011, 33(2): 309-314.

LIU B, TAO W, DOU G Q, et al. Weighted symbol-flipping decoding for nonbinary LDPC codes based on a new stopping criterion[J]. Journal of Electronics & Information Technology, 2011, 33(2): 309-314.

[11] GARCI-HERRERO F, LI E, DECLERCQ D, et al. Multiple-vote symbol-flipping decoder for nonbinary LDPC codes[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2014, 22(11): 2256-2267.

[12] ZHAO S, MA X, ZHANG X, et al. A class of nonbinary LDPC codes with fast encoding and decoding algorithms[J]. IEEE Transactions on Communications, 2013, 61(1): 1-6.

[13] CHAO C H, CHI J W, CHAO Y C, et al. Parallel symbol-flipping decoding for non-binary LDPC codes[J]. IEEE Communications Letters, 2013, 17(6): 1228-1231.

[14] GUO F, HANZO L. Reliability ratio based weighted bit-flipping decoding for low-density parity-check codes[J]. Electronics Letters. 2004, 40(21): 1356-1358.

[15] GARCIA-HERRERO F, DECLERCQ D, VALLS J. Non-binary LDPC decoder based on symbol-flipping with multiple votes[J]. IEEE Communications Letters, 2014, 18(5): 749-752.

[16] 张高远，周亮，文红. 基于幅度和的LDPC码加权比特翻转译码算法[J]. 系统工程与电子技术, 2014, (4): 752-757.

ZHANG G Y, ZHOU L, WEN H. Sum of the magnitude based weighted bit-flipping decoding algorithms for LDPC codes[J]. Systems Engineering and Electronics , 2014, (4): 752-757.

[17] 张高远，周亮，苏伟伟，等. 基于平均幅度的LDPC码加权比特翻转译码算法[J]. 电子与信息学报, 2013,(11): 2572-2578.

ZHANG G Y, ZHOU L, SU W W, et al. Average magnitude based weighted bit-flipping decoding algorithm for LDPC codes[J]. Journal of Electronics & Information Technology, 2013, (11): 2572-2578.

[18] MANKAR M V, PATIL A, ASUTKAR G M. Single mode quasi-cyclic LDPC decoder using modified belief propagation[C]//International Conference on Communications and Signal Processing, Melmaruvathur. India, c2014: 862-866.

Weighted symbol-flipping decoding for non-binary LDPC codes based on average probability and stopping criterion

GUO Rui1, LIU Chun-yu1, WANG Mei-jie1, PAN Peng1, BAO Jian-rong1,2, GUO Chun-sheng1

(1. Communication Engineering Institute, Hangzhou Dianzi University, Hangzhou 310018, China; 2. National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

In order to improve the decoding performance and reduce the decoding complexity of weighted symbols flipping decoding algorithm for nonbinary low density parity-check(LDPC) code, a weighted symbols flipping decoding for nonbinary LDPC codes based on average probability and stopping criterion was proposed. The algorithm puts the average probability of all the information nodes adjacent to the check node as weights to make the flipping-function more effectively and improve the efficiency of the flipping-symbols, and then improves the decoding performance. At the same time, the algorithm adds a stopping criterion controlling decoding iterations to further improve the decoding speed. Simulation results show that compared to WSF algorithm, NSCWSF algorithm(=10) and NSCWSF algorithm(=6), the new algorithm proposed(=10) is gotten about 0.68 dB, 0.83 dB and 0.96 dB gain at the symbol error rate of 10-5in the presence of additive white Gaussian noise(AWGN), meanwhile, the average number of decoding iterations is also reduced by 78.60%~79.32%, 74.89%~75.95% and 67.2%~70.8%, respectively.

non-binary low density parity-check codes, weighted symbols flipping decoding, average probability, stopping criterion, flipping-function

TN911.22

A

10.11959/j.issn.1000-436x.2016029

2015-04-07；

2015-07-30

郭锐，guorui@hdu.edu.cn

浙江省自然科学基金资助项目(No.LY16F010013)；浙江省重点科技创新团队基金资助项目（No.2013TD03）；国家自然科学基金资助项目(No.61471152, No.61401130, No.61001133); 浙江省公益性技术应用研究计划基金资助项目(No.2015C31103)；东南大学移动通信国家重点实验室开放研究基金资助项目(No.2014D02)

Zhejiang Provincial Natural Science Foundation of China (No.LY16F010013), Zhejiang Province Science and Technology Innovation Program Foundation (No.2013TD03), The National Natural Science Foundation of China (No.61471152, No.61401130, No.61001133), Zhejiang Province Public Welfare Technology Application Research Project Foundation (No.2015C31103), Foundation of State Key Laboratory of Mobile Communications. Southeast University (No.2014D02)

郭锐（1980-），男，湖北十堰人，博士，杭州电子科技大学副教授、硕士生导师，主要研究方向为无线通信、信道编码等。

刘春于（1992-），女，河南洛阳人，杭州电子科技大学硕士生，主要研究方向为无线通信、信道编码等。

王美洁（1991-），女，山东烟台人，杭州电子科技大学硕士生，主要研究方向为无线通信、信道编码等。

潘鹏（1983-），男，浙江丽水人，博士，杭州电子科技大学副教授、硕士生导师，主要研究方向为无线通信、多天线技术等。

包建荣（1978-），男，浙江杭州人，博士，杭州电子科技大学副教授、硕士生导师，主要研究方向为无线通信、信道编码等。

郭春生（1971-），男，甘肃武威人，博士，杭州电子科技大学副教授、硕士生导师，主要研究方向为视频分析与模式识别。