MapReduce框架下支持差分隐私保护的k-means聚类方法

李洪成，吴晓平，陈燕



MapReduce框架下支持差分隐私保护的-means聚类方法

李洪成1，吴晓平1，陈燕2

（1. 海军工程大学信息安全系，湖北武汉 430033；2. 解放军61062部队，北京 100091）

针对传统隐私保护方法无法应对任意背景知识下恶意分析的问题，提出了分布式环境下满足差分隐私的-means算法。该算法利用MapReduce计算框架，由主任务控制-means迭代执行；指派Mapper分任务独立并行计算各数据片中每条记录与聚类中心的距离并标记其属于的聚类；指派Reducer分任务计算同一聚类中的记录数量和属性向量之和，并利用Laplace机制产生的噪声扰动和，进而实现隐私保护。根据差分隐私的组合特性，从理论角度证明整个算法满足-差分隐私保护。实验结果证明了该方法在提高隐私性和时效性的情况下，保证了较好的可用性。

数据挖掘；-均值聚类；MapReduce；差分隐私保护；Laplace机制

1 引言

数据挖掘作为信息获取的一种重要方法，可以从体量巨大、快速更新、类型多样、价值量大的大数据中挖掘出有用的信息。聚类分析是一种典型的非指导学习数据挖掘方法，主要思想是将数据分为若干类，使各聚类中的数据差别最小、聚类之间的数据差别最大，该方法在网络入侵异常检测、大规模选址和市场细分等领域有重要应用。

在大数据的背景下，聚类分析技术主要面临以下2个问题。1) 随着大数据时代的数据体量越来越巨大，单个计算机难以在可接受的时间内对数据进行有效的聚类分析。因此，如何利用并行分布式计算资源进行快速聚类分析[1]是亟待解决的关键问题。2) 数据聚类分析的结果在提供有价值信息的同时，可能会泄露数据集中单个记录的信息，对数据隐私安全造成威胁。在大数据时代，攻击者所拥有的背景知识越来越多，使攻击者窃取数据隐私更加便利[2]。因此，研究应对任意背景知识的隐私保护聚类分析技术成为隐私保护领域的研究焦点。

国内外学者做了许多卓有成效的研究工作。其中，文献[3]在云计算平台上采用高效的MapReduce并行计算模型实现了-means聚类算法｡该算法首先利用MapReduce的映射函数计算各条记录到聚类中心的距离，并标记其属于的聚类中心，然后利用规约函数计算出新的聚类中心，最后启用新的MapReduce Job来进行-means算法的下一轮迭代，进而将-means算法每轮迭代中时间复杂度最高的步骤交由分布式计算资源处理，有效提高了-means算法的运行效率。在提高聚类分析时效性的同时，云平台的开放性使攻击者拥有大量的攻击背景知识[4]，攻击者可以通过关联背景知识和聚类结果来窃取数据隐私[5,6]。然而，传统的隐私保护方法只能应对特定背景知识下的攻击，针对此问题，文献[7]利用差分隐私保护的严格定义，提出了可以应对任意背景知识下攻击的-means聚类方法DP-means（differential private-means），该方法通过对-means算法每轮迭代中各聚类内记录之和和记录数等中间变量加入适量随机噪声来实现隐私保护。此外，文献[8,9]针对DP-means中初始聚类中心受随机噪声影响较大的问题，对DP-means算法的初始中心点选择方法进行了改进，有效提高了聚类分析的可用性。以上文献并没有研究将DP-means部署于分布式环境的具体方法，也就没有解决分布式环境下应对任意背景知识的数据隐私保护问题。

基于此，本文提出了一种MapReduce框架[10]下支持差分隐私保护的-means聚类方法，利用MapReduce框架提供的分布式计算功能来提高聚类分析的效率，并通过随机噪声添加使聚类的输出结果满足差分隐私。

2 差分隐私保护

差分隐私保护是一种基于部分信息隐藏的隐私保护技术，该技术通过随机响应或随机噪声添加来实现信息干扰，同时使干扰后的输出信息在一定程度上保持原有的统计特性，进而使数据挖掘结果的可用性保持在可接受的范围内。

差分隐私技术给出了一个严格且可证明的隐私保护定义，保证在数据集中改变任一条记录时，查询结果的变化量极小，攻击者在已知除目标记录外所有其他记录信息的条件下，仍然无法分析出这条记录的任何信息，因此该方法可以应对任意背景知识下的恶意分析[11]。差分隐私保护的基本原理如下。

用户从数据集中提取信息的操作被定义为查询，算法对查询的输出进行随机化处理，使之满足差分隐私保护的条件[12]。

定理1 假设数据集和完全相同或只相差一条记录，()为一个随机算法输出的值域，[]为事件发生的可能性，如果对于任意∈()，有

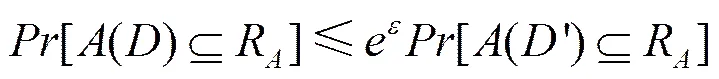
则随机算法提供-差分隐私保护，其中，参数称为隐私保护预算。

全局敏感度是查询函数的一条重要固有属性，反映单个记录变化对查询函数输出的影响。全局敏感度的定义如下。

定义1查询的全局敏感度为

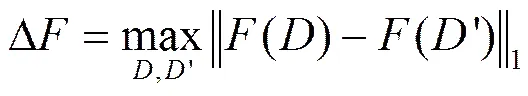
差分隐私保护的实现机制主要有Laplace机制与指数机制2种，分别利用随机噪声添加和随机响应的方式实现隐私保护。其中，Laplace机制适用于对数值型结果的保护[13]，是聚类分析中最常用的差分隐私保护机制，其原理如下。

定理2 对于查询，数据集，设查询输出为()，的全局敏感度为Δ，如果噪声服从尺度为的拉普拉斯分布，则算法满足-差分隐私[13]。

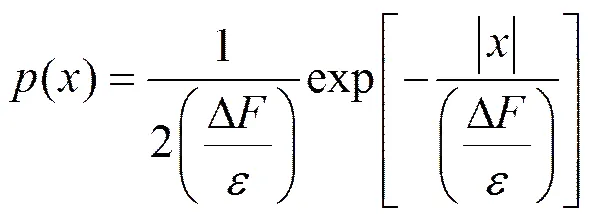
此外，差分隐私保护具有序列组合性和并行组合性2种组合特性，这些特性在证明算法是否满足差分隐私以及在隐私预算分配过程中起着重要作用[14]。

性质1 设有个随机算法1,…,A，算法A(1≤≤)提供ε-差分隐私保护，则对于同一数据集，{1,…,A}在上的序列组合算法提供-差分隐私保护，其中，。

性质2 设有随机算法和数据集，将分为不相交的子集1,…,D，若算法提供-差分隐私保护，则在{1,…,D}上的组合运算所构成的算法提供-差分隐私保护。

3 MapReduce框架下的DP k-means算法

本文算法的功能是在MapReduce分布式环境下，保证在数据集中改变任一记录时，每个聚类的质心以及记录数量所发生的变化不泄露隐私信息，即恶意分析者无法利用其拥有的与原数据集相似的数据集，通过挖掘得到原数据集中单个记录的隐私信息。算法应对的攻击模型如图1所示。

算法的基本思路是利用分布式计算节点上的Map分任务判断出各记录属于的聚类类别，利用Reduce分任务计算出聚类中的记录数量和对应属性之和，并加入适量Laplace噪声，使聚类分析的结果满足-差分隐私。

传统的差分隐私保护-means算法[7]存在聚类准确性较低的问题，其主要原因是随机选择的初始中心点导致算法收敛速度较慢，而算法迭代次数的增多导致了每轮添加的噪声增多，而且添加了噪声的初始中心点往往与原中心点偏离较远[9]，这些问题均导致了算法的聚类准确性较低，所以本算法在对差分隐私保护-means算法进行MapReduce并行化设计时，采用改进的初始中心点选择和加噪方法。

3.1 算法设计

设数据集中的记录总数为，各条记录记为a(1≤≤)，各记录的维数为；将这些记录分为个数据片，各数据片记为D(1≤≤)；算法要求的聚类数目为，各聚类中心记为u(1≤≤)。算法的步骤如下。

Step1 主任务Driver首先将各记录归一化到[0, 1]空间中。将条记录1,…,a平均分成个子集1,…,C，集合C中的记录数|C|≤，()为向上取整函数[8]。计算C中记录的数量和C中各记录的属性向量之和，分别对和加入随机噪声得到和，计算0，即为初始聚类中心点。

Step2 主任务将所有数据记录平均分为个数据片，并指派个分任务执行Map操作，指派个分任务执行Reduce操作。

Step4 Reducer分任务接收所有同属于一个聚类中心的<，>对，运行Reduce函数：计算该聚类中记录的数量和聚类内各记录的属性向量之和，对和加入随机噪声，然后计算加噪后的聚类中心点。

Step5 主任务接收各个Reduce节点的输出结果，计算本轮和上一轮中个聚类中心点的距离。若中心点属性向量差的距离范数小于阈值，则算法终止，输出各聚类中心和聚类内记录的数量；否则，重复Step3~Step5。

MapReduce框架下的DP-means算法流程如图2所示。

3.2 隐私性分析

由图2可以看出，MapReduce框架下DP-means算法的隐私性通过对每个Reduce操作中的num和sum加入Laplace噪声来实现。由于-means算法的每轮迭代相当于随机算法的序列组合，所以根据性质1可知，整个算法的隐私保护预算为

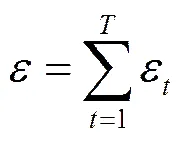
其中，为迭代的总次数，ε为第次迭代的隐私保护预算。在预算分配方面，本文采用文献[7]的策略，每次迭代消耗剩余隐私预算的一半，即第次迭代的隐私预算为ε=。

图2 MapReduce框架下的DP -means算法

在每轮迭代中，由于个Reducer分节点相互独立地执行操作，各轮迭代的结果相当于Reduce操作的并行组合[15]，所以根据性质2可知，要想第轮迭代满足ε-差分隐私，需要使分布式环境下每个Reducer分任务的操作满足ε-差分隐私。

由定义1可知，的全局敏感度Δnum=1，在维空间[0, 1]的点集中添加或删除一个点，各个属性和的最大变化量为1，由于点的维数为，则的全局敏感度Δsum=｡所以根据性质1可知，整个查询序列的全局敏感度Δ=+1。

因此，由定理2可知，在初始中心点计算过程中的0和0上分别加入随机噪声(1)，并在算法第轮迭代的num和sum上分别加入随机噪声(1)，可以保证MapReduce框架下DP-means算法满足-差分隐私保护。相比于传统的差分隐私保护-means算法，改进的初始中心点计算过程可以在相同的隐私保护预算下，减少算法的迭代次数，进而减少随机噪声添加量。

4 算法效率及可用性实验

由于本文算法的主要功能是利用MapReduce分布式计算框架提高聚类效率，并利用Laplace机制保护数据隐私，而算法的隐私性已经在上文中得到证明，因此本文的实验部分只考虑算法的运行效率，以及隐私保护聚类算法的输出结果可用性。

实验中云计算平台由1台主节点的计算机和3台分节点的计算机组成，每台计算机配置如下：操作系统为Linux，CPU为3.30 GHz，内存为2.99 GB。在集群上部署Hadoop0.20.2。聚类算法利用Java软件进行开发。

实验所选择的数据集为UCI Knowledge Discovery Archive database中的“Blood”数据集（记录数为748，属性数为5，数据类型为实值型）和“gamma”数据集（记录数为19 020，属性数为10，数据类型为实值型），这2个数据集中均给出了各记录的分类信息，因此可以用来检验聚类算法的性能。根据“Blood”和“gamma”数据集的标准分类结果，实验设定聚类中心数为2，相邻2轮中心点属性向量差的距离范数小于1时迭代终止。

4.1 算法运行效率实验

为反映MapReduce框架下算法运行效率受分布式计算节点数量的影响，本实验启动1个和3个分节点分别进行运算，并考察不同数据量情况下加速比的变化规律。首先，在“gamma”数据集上截取不同数量的记录作为待处理文件，分别上传至Hadoop的HDFS文件系统中。然后，将本文算法部署于MapReduce中，记录5次运行时间的平均值，得到1个和3个子节点分别参与运算的情况下算法的运行时间（如图3所示）。

由图3可以看出，系统启动3个子节点时算法的运行时间较启动1个子节点时显著减少，说明分布式集群可以有效提高本文聚类算法的运行效率。然而，随着数据集记录数量的增多，运行效率的提高比例逐渐降低。主要原因是记录数量的增涨导致算法迭代次数增加，而每轮迭代中都有主节点与子节点之间的数据传递操作，以及主节点进行的聚类中心距离比较操作，这些操作没有利用分布式集群的资源，因此操作用时随着迭代次数增加而增加，而不随子节点数目增加而减少。

另外，为反映本文算法引入隐私保护后对算法效率的影响，将本文算法与分布式计算框架下的-means算法进行比较。由于文献[3]算法将-means算法部署于MapReduce环境中，而没有引入隐私保护，所以选择文献[3]算法作为比较对象。首先，在包含1个主节点和3个分节点的分布式计算平台上，分别利用本文算法和文献[3]算法处理“gamma”数据集上截取的不同文件，记录5次运行时间的平均值，得到本文算法运行时间减去文献[3]算法运行时间的差值（如图4所示）。

通过比较图3和图4中数值的数量级，可以看出2种算法运行时间的差值比算法运行时间要小约4个数量级。因此，相比于文献[3]算法，本文算法在提高隐私性的情况下，并没有导致运行效率的明显降低。此外，由图4可以看出，2种算法运行时间的差值随着数据集记录数量的增涨而增大。主要原因是随着记录数量的增长，算法的迭代次数逐渐增加，而本文算法的每轮迭代都要进行Laplace随机噪声的产生和添加操作，每轮迭代中的这些操作直接导致了2种算法运行时间的差别。

4.2 聚类结果可用性实验

为衡量本文提出的MapReduce框架下差分隐私聚类算法的可用性，本实验选择以下参考标准与本文算法聚类结果进行比较：1)由于“Blood”和“gamma”数据集中的标准分类情况是在真实情况下调查得到的，因此选择“Blood”和“gamma”数据集的标准分类结果作为比较对象之一；2) 为了分析本文算法引入隐私保护后对聚类结果可用性的影响，本实验选择文献[3]算法的聚类结果作为可用性比较的另一个参考对象。

衡量数据挖掘结果可用性的指标主要有准确率（precision）和召回率（recall）等，而F-measure可以对准确率和召回率进行综合，因此本实验利用F-measure评价指标来衡量聚类可用性｡F-measure越大说明2个聚类结果的相似程度越强，即本文算法所添加的噪声对聚类可用性影响越小｡

F-measure的计算过程如下：用表示作为参考标准的聚类结果，表示本文聚类算法的聚类结果，聚类数为，U为中的第个聚类集合（1≤≤），V为中的第个聚类集合（设2次聚类的标记统一），cover为U和V重合的记录数目，|U|和|V|分别为U和V中的记录数目，记第个聚类的准确率为P，召回率为R，则

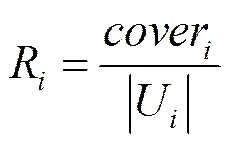
(6)

然后，计算P和R的加权调和平均，记为F，则

最后，对各聚类的F进行加权平均。设TOTAL为数据集记录总数，算得聚类结果的可用性度量

(8)

将本文算法的聚类结果与数据集中标准分类结果的相似程度记为F-measure1，并将本文算法的聚类结果与文献[3]算法聚类结果的相似程度记为F-measure2。由于算法每次运行时噪声的添加量服从Laplace随机分布，所以聚类结果具有一定的随机性，因此实验中的结果取10次运算的平均值。对于“Blood”和“gamma”数据集，当隐私保护预算变化时，F-measure1和F-measure2的变化情况如图5所示。

(a)“Blood”数据集聚类结果的F-measure变化情况

(b)“gamma”数据集聚类结果的F-measure变化情况

图5 各数据集的F-measure1和F-measure2随变化情况

由图5可以看出，当隐私保护预算大于3时，本文算法的聚类结果可用性达到较高水平，因此本文算法可以在实现隐私性的情况下，保证聚类结果具有较好的可用性｡另外，图4中当隐私保护预算较小时，聚类结果的可用性随着隐私保护预算的增加而显著增加，当增大到一定值时，聚类结果可用性的增加速度趋于平缓，而考虑到隐私保护预算与添加噪声的尺度参数成反比，因此用本文算法处理“Blood”和“gamma”数据集时，隐私保护预算取3~4有利于实现算法隐私性和可用性的平衡。

5 结束语

本文利用MapReduce计算框架实现了并行分布式-means聚类，并同时利用Laplace机制实现了算法的差分隐私保护，同时提高了-means算法的时效性和隐私性。下一步需要进行的研究工作主要有以下2个方面：1) 针对算法迭代次数对运行效率影响较大的问题，设计算法减少MapReduce Job的运行次数，并将-means中的迭代执行判断工作交由子节点执行；2) 为缓解算法隐私性和可用性之间的矛盾，研究如何在保证隐私保护水平的前提下，通过综合利用指数机制和Laplace机制，减少对每轮迭代实施的扰动。

[1] FLAVIO C, NILESH D, RAVI K. Correlation clustering in MapReduce[C]//The 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2014). New York, USA, c2014: 641-650.

[2] 孟小峰, 张啸剑. 大数据隐私管理[J]. 计算机研究与发展, 2015, 52(2):265-281.

MENG X F, ZHANG X J. Big data privacy management[J]. Journal of Computer Research and Development, 2015, 52(2):265-281.

[3] 江小平, 李成华, 向文, 等.-means聚类算法的MapReduce并行化实现[J]. 华中科技大学学报（自然科学版）, 2011, 39(S1): 120-124.

JIANG X P, LI C H, XIANG W, et al. Parallel implementing-means clustering algorithm using MapReduce programming mode[J]. Journal of Huazhong Univ of Sci & Tech(Natural Science Edition), 2011, 39(S1):120-124.

[4] ROY I, SETTY S T V, KILZER A, et al. Airavat: security and privacy for MapReduce[C]//The 7th USENIX Symposium on Networked Systems Design and Implementation. San Jose, USA, c2010:297-312.

[5] 肖人毅. 云计算中数据隐私保护研究进展[J]. 通信学报, 2014, 35(12):168-177.

XIAO R Y. Survey of privacy preserving data queries in cloud computing[J]. Journal on Communications, 2014, 35(12):168-177.

[6] SHI E, CHAN T H, RIEFFEL E G,. Privacy-preserving aggregation of time-series data[C]//The Network and Distributed System Security Symposium. San Diego, USA, c2011.

[7] DWORK C. A Firm Foundation for Private Data Analysis[J]. Communications of the ACM, 2011, 54(1):86-95.

[8] 李杨, 郝志峰, 肖燕珊, 等. 差分隐私DPE-means 数据聚合下的多维数据可视化[J]. 小型微型计算机系统, 2013, 34(7):1637-1640.

LI Y, HAO Z F, XIAO Y S, et al. Multidimensional data visualization using aggregation method of differential privacy equip partition k-means[J]. Journal of Chinese Computer Systems, 2013, 34(7): 1637-1640.

[9] 李杨, 郝志峰, 温雯, 等. 差分隐私保护-means聚类方法研究[J]. 计算机科学, 2013, 40(3):287-290.

LI Y, HAO Z F, WEN W, et al. Research on differential privacy preserving-means clustering[J]. Computer Science, 2013, 40(3): 287-290.

[10] 何清, 庄福振, 曾立, 等. PDMiner: 基于云计算的并行分布式数据挖掘工具平台[J]. 中国科学: 信息科学, 2014, 44(7):871-885.

HE Q, ZHUANG F Z, ZENG L, et al. PDMiner: a cloud computing based parallel and distributed data mining toolkit platform[J]. Chinese Science: Information Science, 2014, 44(7):871-885.

[11] MCGREGOR A, MIRONOV I, PITASSI T, et al. The limits of two-party differential privacy[C]//The 51st IEEE Annual Symposium on Foundations of Computer Science. Las Vegas, USA, c2010:81-90.

[12] 熊平, 朱天清, 王晓峰. 差分隐私保护及其应用[J]. 计算机学报, 2014, 37(1):101-122.

XIONG P, ZHU T Q, WANG X F. A survey on differential privacy and applications[J]. Chinese Journal of Computers, 2014, 37(1):101-122.

[13] 丁丽萍, 卢国庆. 面向频繁模式挖掘的差分隐私保护研究综述[J]. 通信学报, 2014, 35(10):200-209.

DING L P, LU G Q. Survey of differential privacy in frequent pattern mining[J]. Journal on Communications, 2014, 35(10):200-209.

[14] 张啸剑, 孟小峰. 面向数据发布和分析的差分隐私保护[J]. 计算机学报, 2014, 37(4):927-949.

ZHANG X J, MENG X F. Differential privacy in data publication and analysis[J]. Chinese Journal of Computers, 2014, 37(4):927-949.

[15] MCSHERRY F. Privacy integrated queries: an extensible platform for privacy-preserving data analysis[J]. Communication of the ACM, 2010, 53(9):89-97.

-means clustering method preserving differential privacy in MapReduce framework

LI Hong-cheng1, WU Xiao-ping1, CHEN Yan2

(1. Department of Information Security, Naval University of Engineering, Wuhan 430033, China; 2. No.61062 Troops of PLA, Beijing 100091, China)

Aiming at the problem that traditional privacy preserving methods were unable to deal with malign analysis with arbitrary background knowledge, a-means algorithm preserving differential privacy in distributed environment was proposed. This algorithm was under the computing framework of MapReduce. The host tasks were obligated to control the iterations of-means. The Mapper tasks were appointed to compute the distances between all the records and clustering centers and to mark the records with the clusters to which the records belong. The Reducer tasks were appointed to compute the numbers of records which belong to the same clusters and the sums of attributes vectors, and to disturb the numbers and the sums with noises made by Laplace mechanism, in order to achieve differential privacy preserving. Based on the combinatorial features of differential privacy, theoretically prove that this algorithm is able to fulfill-differentially private. The experimental results demonstrate that this method can remain available in the process of preserving privacy and improving efficiency.

data mining,-means clustering, MapReduce, differential privacy preserving, Laplace mechanism

TP301

A

10.11959/j.issn.1000-436x.2016038

2015-04-05；

2015-07-28

国家自然科学基金资助项目（No.61100042）；总后军内科研基金资助项目（No.AWS14R013）

The National Natural Science Foundation of China (No.61100042), The Military Scientific Research Project of the General Logistics Department (No.AWS14R013)

李洪成（1991-），男，河南商丘人，海军工程大学博士生，主要研究方向为信息安全、数据挖掘。

吴晓平（1961-），男，山西新绛人，海军工程大学教授、博士生导师，主要研究方向为信息安全、密码学。

陈燕（1975-），女，河北石家庄人，解放军61062部队高级工程师，主要研究方向为网络应用、信息系统。