VI-2类5维q元线性码的汉明重量谱的确定

胡国香，张焕国



VI-2类5维元线性码的汉明重量谱的确定

胡国香1,2，张焕国1

（1. 武汉大学计算机学院，湖北武汉 430072；2. 中南民族大学数学与统计学学院，湖北武汉 430074）

上线性码的汉明重量谱为序列，其中，d是的维子码的最小支撑重量。第VI类5维元线性码的汉明重量谱，按照新的必要条件可以分成6个子类。运用有限射影几何方法研究VI-2类的5维元线性码的汉明重量谱，确定VI-2类5维元线性码的几乎所有汉明重量谱。

汉明重量；线性码；差序列；射影几何

1 引言

通信系统中信息的传递离不开编码，而汉明重量是编码理论中非常重要的基本概念，与编码中码的检错以及纠错能力息息相关。编码理论的创始人之一汉明（Hamming）提出了汉明重量。广义汉明重量最初是由用于第2类窃密信道的线性编码方案所触动而提出的。假设发送者有bit信息被编成bit码后通过此信道传送给接收者。入侵者能够从信道码中随意窃取到其中的bit数据。传送的信道假设是无噪的，因而正确译码没有问题。问题的焦点是如何阻止入侵者获太多的信息，也就是设计出一种编码方案，使入侵者截取bit数据时，对于数据的可疑度(不确定度)尽可能得大。事实上，当一种线性码用于上述信道时，广义汉明重量可以完全表现出该码的特性。线性码的广义汉明重量谱是Wei[1]首次正式提出的，广义汉明重量是码的最小距离的推广。线性码是编码理论中一类非常重要的码，很多其他形式的码都可以和线性码找到一定的联系。汉明重量的另一种形式被Forney称作长度/维数轮廓，在线性码的格子复杂度分析[2~6]、译码分析[7~9]、检错分析[10]等方面都有非常重要的应用，文献[11]也详细讨论了其应用。重量谱的概念由Wei提出以后，立即成为编码理论的一个前沿研究热点。

1.1 基础知识

对于一个码，中的所有码字的非零位置的全体所构成的集合称为的支撑集，记为，即，支撑集的大小记为。

“如何确定线性码的汉明重量谱”一直是编码理论研究的核心问题。关于汉明重量谱的研究，第1个研究方向是关于具体的各类线性纠错码的。由于确定是编码理论中尚未完全解决的难题，因此的确定更加困难，目前仅有少数的几类码确定了重量谱。文献[12]确定了RM码、汉明码及其补码、扩展汉明码、极大距离可分码等的重量谱；文献[13~15]对广义汉明重量的上下限进行了研究；文献[16,17]中，重量谱的类别被扩展到线性等重码。第2个方向是关于一般线性码的。对于一般线性码的重量谱，传统的研究方法有组合方法与计算机搜索。但是随着线性码维数的增加，重量谱的类别也呈指数增加，对于高维数线性码重量谱的研究更加困难，这2种方法均不太适用。目前来看，有限射影几何方法对于高维数线性码重量谱的研究较为适用。

1.2 相关工作

1992年，密码学家Helleseth[18]提出了确定一般线性码的所有可能的汉明重量谱，这也是编码理论中一个非常有意义的理论问题。1996年，陈文德等[19]提出了有限射影几何方法，并第一次有效地用于确定4维元线性码的汉明重量谱。他们还把4维元线性码及其汉明重量谱分成了9类，用有限射影几何方法取得了丰富的分类研究成果，参见文献[20,21]等。文献[22]对4维元线性码的汉明重量谱进行研究，确定4维元线性码的几乎所有的汉明重量谱。文献[23]中把5维元线性码及其汉明重量谱分成6类，并对6类码中的II-1类进行了研究；文献[24]对II-2类进行了研究。文献[25]确定了5维元线性码V-1类的几乎所有的汉明重量谱。文献[26]确定了5维元线性码V-2类的几乎所有的汉明重量谱。在文献[27]中第VI类5维元线性码的汉明重量谱又被分成了6个子类，并对其中的VI-1类进行研究，确定该类的几乎所有的汉明重量谱。本文将对文献[27]中的VI-2子类进行研究，并确定其几乎所有的汉明重量谱。

本文主要研究了文献[27]中5维元线性码的第VI-2类的汉明重量谱。利用有限射影几何方法，通过往4维空间进行投影，把重量谱的确定转化为4维空间中的点、线、面、体的赋值函数的确定问题，使确定重量谱这一抽象的理论问题变得更为形象化。

2 预备知识

(1)

3 主要结果

文献[27]中把5维元线性码的第VI类的差序列的必要条件分成6个子类，并对其中的VI-1类进行了研究，其他5个子类的重量谱均未确定。相比VI-1类来说，VI-2重量谱的确定更为困难，因为当取得上界时，赋值函数的取值不完全为的整数倍，需要考虑将进行分数化处理。

本文研究这6类中的VI-2个子类。由文献[27]可得VI-2类差序列的必要条件如下。

下面将构造出VI-2类的几乎所有可能的汉明重量谱，即证明上述必要条件是几乎充分的，以下的引理1～引理4将给出各种条件下的详细证明与赋值函数的构造。

引理1 设

(3)

(4)

证明 把式(2)～式(5)代入后，得

定义下面这些符号为

点、线、面、体之间的关系说明如下。

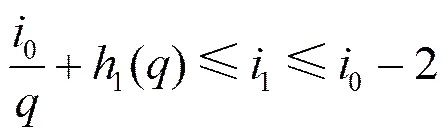
证明 定义以下一些符号（如图2所示）。

所以可令

证明 先定义以下一些符号（如图3所示）。

1) 由点的非负性，可得

又由

又由

又由

又由

3）由面之间的关系可得

又由

1) 由点的非负性，可得

又由

3) 由面之间的关系，可得

又由

所以，

由上述引理1～引理4，可得如下的定理。

所以，由引理1～引理4，该定理的充分性得证，也就得到了VI-2类的几乎所有的差序列。

4 结束语

本文对5维元线性码中的第VI-2类进行研究，运用有限射影几何方法通过对射影空间中的点进行赋值，得到不同条件下赋值函数的构造，从而得到第VI-2类5维元线性码的几乎所有的汉明重量谱。

[1] WEI V K. Generalized Hamming weight for liner codes[J]. IEEE Transactions Information Theory, 1991,37(5):1412-1418.

[2] FORNEY G D. Dimension/length profiles and trellis complexity of liner block codes[J]. IEEE Transactions Information Theory, 1994, 40(6):1741-1752.

[3] KASAMI T, TAKATA T, FUJIWARA T, et al. On the optimum bit orders with respect to the state complexity of trellis diagrams for binary linear codes[J]. IEEE Transactions Information Theory, 1993, 39(1): 242-245.

[4] MORELOS-ZARAGOZA R, FUJIWARA T, KASAMI T, et al. Constructions of generalized concatenated codes and their trellis-based decoding complexity[J]. IEEE Transactions Information Theory, 1999, 45(2): 725-731.

[5] SHANY V, BE’ERY Y. The preparata and goethals codes: trellis complexity and twisted squaring constructions[J]. IEEE Transactions Information Theory, 1999, 45(5): 1667-1673.

[6] VARDY A, BE’ERY Y. Maximum-likelihood soft decision decoding of BCH codes[J]. IEEE Transactions Information Theory, 1994, 40(2): 546-554.

[7] FOSSORIER M P C, LIN S. A unified method for evaluating the error-correction radius of reliability-based soft-decsion algorithms for linear block codes[J]. IEEE Transactions Information Theory, 1998, 44(2): 691-700.

[8] FOSSORIER M P C, LIN S, SNYDERS J. Reliability-based syndrom decoding of linear block codes[J]. IEEE Transactions Information Theory, 1998, 44(1): 388-398.

[9] GAZELLE D, SNYDERS J. Reliability-based code-search algorithms for maximum-likelihood decoding of block codes[J]. IEEE Transactions Information Theory, 1997, 43(1):239-249.

[10] KLØVE T. The worst-case probability of undetected error for linear codes on the local binomial channel[J]. IEEE Transactions Information Theory, 1996, 42(1): 172-179.

[11] 岳殿武,酆广增.广义Hamming重量,维数/长度轮廓及其应用[J].电子学报,1999,27(4):111-115.

YUE D W, FENG G Z. Generalized Hamming weight, dimension/length profile and their applications[J]. Chinese Journal of Electronics, 1999, 27(4):111-115.

[12] 罗守山,陈萍,杨义先.广义汉明重量下限函数L()的新证明[J].北京邮电大学学报,1996,19(4):67-70.

LUO S S, CHEN P, YANG Y X. A new proof of lower boundL() of generalized Hamming weights[J]. Beijing University of Posts and Telecommunications, 1996,19(4):67-70.

[13] 罗守山,杨义先,吴伟陵.线性码广义汉明重量的上限函数[J].通信学报, 1999,20(11):86-90.

LUO S S, YANG Y X, WU W L.The upper bound of generalized Hamming weight of linear codes[J]. Journal on Communications, 1999, 20(11):86-90.

[14] 岳殿武,胡正名.广义Hamming重量上/下界的对偶定理[J].通信学报,1997,18(7):76-78.

YUE D W, HU Z M. A dual theorem of upper and lower bounds on the generalized Hamming weights[J]. Journal on Communications, 1997, 18(7):76-78.

[15] 岳殿武,胡正名.关于BCH码的广义Hamming重量上下限[J].通信学报,1997,18(4):75-79.

YUE D W, HU Z M. Upper bounds and lower bounds on generalized Hamming weight for BCH codes[J]. Journal of Communications, 1997, 18(4):75-79.

[16] 岳殿武,胡正名.广义Hamming重量和等重码[J].电子科学学刊, 1997,19(4):553-557.

YUE D W, HU Z M. Generalized Hamming weights and equal weight codes[J]. Journal of Electronics, 1997,19(4):553-557.

[17] 岳殿武,江凌云,段冰娟.线性等重码格子复杂度的确定[J].应用科学学报,2000,18(1):68-71.

YUE D W, JIANG L Y, DUAN B J. The determination of trellis complexity of linear constant weight codes[J]. Journal of Applied Sciences, 2000,18(1):68-71.

[18] HELLESETH T, KLØVE T , YTREHUS Ø. Generalized Hamming weights of linear codes[J]. IEEE Transactions Information Theory, 1992, 38(3): 1133-1140.

[19] CHEN W D, KLØVE T. The weight hierarchies of-ary codes of dimension 4[J]. IEEE Transactions Information Theory, 1996, 42(7): 2265-2272.

[20] CHEN W D, KLØVE T. Bounds on the weight hierarchies of linear codes of dimension 4[J]. IEEE Trans Inform Theory, 1997, 43(6): 2047-2054.

[21] CHEN W D, KLØVE T. The weight hierarchies of-ary codes of dimension 4[J]. IEEE Transactions Information Theory, 1996, 42(7):2265-2272.

[22] HU G X, CHEN W D. The weight hierarchies of q-ary linear codes of dimension 4[J]. Discrete Mathematics, 2010, 310(24):3528-3536.

[23] 王丽君，陈文德.5维元线性码重量谱的分类与确定[J].系统科学与数学，2011，31(4)：402-413.

WANG L J, CHEN W D. The classification and determination on weight hierarchies of-ary linear codes of dimension 5[J]. Journal of Systems Science and Complexity, 2011, 31(4): 402-413.

[24] 王丽君, 陈文德.II2类5维元线性码的重量谱[J].数学的实践与认识, 2011, 41(21): 244-252.

WANG L J, CHEN W D.MathematicsinPracticeandTheory, 2011, 41(21):244-252.

[25] 王丽君，陈文德.一类5维元线性码重量谱的确定[J].科学通报，2011,56(25):2150-2155.

WANG L J, CHEN W D.

[26] 王丽君，陈文德. V2类5维元线性码的重量谱[J].数学的实践与认识，2012，42(5)：237-245.

WANG L J, CHEN W D. The weight hierarchies of-ary linear codes of dimension 5 in class V2[J]. Mathematics in Practice and Theory, 2012, 42(5):237-245.

[27] HU G X, ZHANG H G, WANG L J, et al. A class of the Hamming weight hierarchy of linear codes with dimension 5[J]. Tsinghua Science and Technology, 2014, 19(5):442-451.

VI-2 class of Hamming weight of-ary linear codes with dimension 5

HU Guo-xiang1,2, ZHANG Huan-guo1

(1. School of Computer, Wuhan University, Wuhan 430072, China; 2. School of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

The Hamming weight hierarchy of a linearcodeoveris the sequence, whereis the smallest support weight of an-dimensional subcode of. According to some new necessary conditions, the VI class Hamming weight hierarchies of-ary linear codes of dimension 5 can be divided into six subclasses. By using the finite projective geometry method, VI-2 subclass and determine were researched almost all weight hierarchies of the VI-2 subclass of weight hierarchies of-ary linear codes with dimension 5.

Hamming weight, linear codes, difference sequence, projective geometry

TN 911.2

A

10.11959/j.issn.1000-436x.2016035

2015-02-02；

2015-04-20

国家自然科学基金资助项目（No.61303212, No.61170080, No.61332019, No.U1135004）；湖北省自然科学基金资助项目（No.2014CBF440）

The National Natural Science Foundation of China (No.61303212, No.61170080, No.61332019, No.U1135004),The Natural Science Foundation of Hubei Province (No.2014CBF440)

胡国香（1978-），女，山东烟台人，武汉大学博士生，中南民族大学副教授，主要研究方向为密码学与信息全安全。

张焕国（1945-），男，河北元氏人，武汉大学教授、博士生导师，主要研究方向为信息安全、可信计算、容错计算与计算机应用等。