基于变分贝叶斯推断的新型全局频谱协作感知算法

吴名，宋铁成，胡静，沈连丰



基于变分贝叶斯推断的新型全局频谱协作感知算法

吴名，宋铁成，胡静，沈连丰

(东南大学移动通信国家重点实验室，江苏南京 210096）

为了实现多维动态频谱接入，首先给出了主用户的全局功率谱近似模型，并构建了新型全局频谱协作感知算法的总体流程，以获得主用户网络中占用频段、功率及位置等全局信息。接着利用变分贝叶斯推断技术，设计了相应的模型系数向量估计器。仿真结果表明，该方法采用的近似模型具有较好的准确性，相应的系数向量估计算法具有较高的有效性和收敛稳定性，同时指明了信噪比和泄漏总虚假功率的关系以及两者对均方误差性能的影响。此外，还证明了该方法通过利用系数向量的稀疏性，而在均方误差性能上具有较大优势。

认知无线电；全局频谱协作感知；变分贝叶斯推断；稀疏性

1 引言

目前，无线通信领域中存在频谱资源日益匮乏而现有频谱利用效率低下这一困境，认知无线电技术正是为解决这一问题而提出的。认知无线电技术的基础和关键是频谱感知技术，该技术主要用于判断授权频段是否被主用户占用。目前，其主要采取协作的方式进行频谱感知，以利用不同从用户的采样点在时间、空间上的独立性或不相关性，实现分集、增强感知性能，从而达到快速、可靠感知的目的[1~3]。

但是因为从用户网络覆盖范围较大，主用户通信范围通常只占据其中一部分。而在其他地方，由于距离主用户较远、主用户信号功率较弱、建筑物遮蔽等原因，从用户对授权频段的使用往往既不会对主用户通信产生有害的干扰，也不会受到主用户的有害影响。同时由于主/从用户一般存在移动性，导致主用户通信影响范围和频谱空洞所处位置也随时间不断变化。由此可知，为实现频谱在多维度上的动态复用，从用户网络如何感知整个覆盖范围中主用户发射机所使用的频段、功率及其所处位置等全局频谱信息成为必须首先解决的问题。文献[4]详细描述了这一问题，并进一步指出由于主/从用户天线所处位置不同导致的路径损耗差异会产生很大的动态频谱复用机会。而文献[5]则介绍了如何利用现代空间统计学来定量描述主/从用户频谱在大范围内分布的统计模型，并指出设计全局频谱分布信息感知算法是实现动态全局频谱共享的首要步骤。而传统的协作感知技术难以完成这种在具有移动性的认知网络中，有效感知其全局频谱信息的任务。因此最近出现多种考虑主/从用户移动性的协作感知算法以实现这一目标。为反映主/从用户移动性导致的频谱接入机会，文献[6]利用两态连续时间马尔可夫链构建信道可用性模型，并根据该模型联合优化频谱感知间隔等参数，以最大化时域/空域频谱接入机会。同时设计相应的信道接入策略，以利用主/从用户移动性导致的各种频谱接入机会。文献[7]利用主/从用户间信道特性、感知数据间相关度和主从用户运动行为构建接近真实的移动性模型，并基于该模型，设计出一种新型的感知节点选择方法，以选择出低相关性、高感知性能的感知节点子集。文献[8]考虑主用户移动性导致的频谱接入机会，由此扩展出新的空时频谱感知模型，并定义一种新的性能评价指标，即受感知参数和移动性影响的从用户可达传输容量。该性能评价指标同时指明了感知机制不完美时，感知机制的精度对信道接入概率的影响，并由此得出最优感知时长，以最大化从用户可达传输容量。文献[9]在不考虑阴影衰落影响的情况下，利用贝叶斯分层先验建模技术设计了新型的协作频谱感知方法，以得到主用户信号的功率谱分布估计值。

本文利用新出现的变分贝叶斯推断技术，设计了一种新型的全局频谱信息协作感知算法。通过最小化全局功率谱模型系数后验函数的K-L（Kullback-Leibler）散度，得到该后验的近似值，然后根据最大后验概率准则得到各主用户发射机占用频段、功率和所处位置3种信息的最优值，由此得到指定区域内全局频谱分布，获得频谱在时间、空间、频谱上的多维信息，使从用户网络可以高效复用空闲频谱。与上述文献相比，这种机制拥有不易受较小局部最优值影响、得到的表达式易于处理等优点。

2 系统建模

假设认知无线网络中有N个主用户发射机正在通信，其位置坐标集合为。在时刻，网络中任意位置x处的从用户接收到的信号y()可以表示为

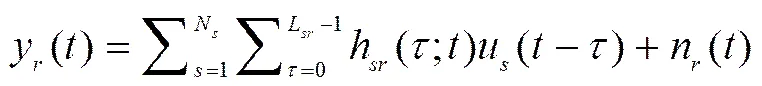
其中，h(;)和u()分别表示第个传输路径上的信道冲激响应和主用户的发射信号，n() 是方差为的加性高斯白噪声，L是主用户和从用户间的传输路径数。

在不考虑噪声的情况下，假设信道h(;)和信号u()都是平稳的，则从用户接收到的单个主用户信号的自相关函数可以表示为。由于信道h()在相干时间内保持不变，所以，则自相关函数可表示为，而接收功率谱可表示为。虽然上式中的信道增益能够通过训练方式获得，但这需要主用户的配合，并拥有区分各主用户信号的能力。因此本文采用一种替代的方法，即路径损耗模型，其中，0、是预先选定的常数。值得强调的是，路径损耗仅影响信道统计量，所以本文考虑的信道冲激响应h(;)都是频率选择性的。

而当存在N个主用户和噪声时，假设信道h(;)和信号u()都是不相关的，从用户的接收功率谱可以表示为

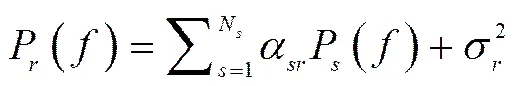
由于感知机制不需要知道功率谱的准确值，所以可利用基扩展模型[10]近似主用户信号的功率谱。如图1所示，带宽为的主用户信号功率谱的基扩展模型由N个不重叠的单位矩形函数γ()组成，其表达式可写为

(3)

其中，θ是模型系数。将式（3）代入式（2）可得

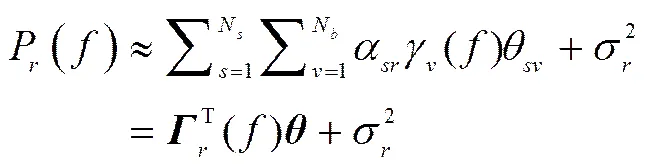
图1 信号功率谱的基扩展近似模型

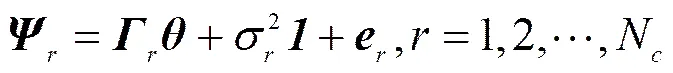
其中，矩阵由构成，表示全1向量，而N表示从用户数量。当每个从用户将自己感知到的功率谱信息和自身的位置发送给融合中心后，融合中心可利用其构建从用户系统接收信号的全局功率谱模型，具体表达式为

(6)

其中，向量、和矩阵是将各从用户的、和按顺序堆叠而成的NN×1维向量和NN×NN维矩阵；而式中，。假设每个从用户可估计出本地噪声功率σ2，由此可改为发送修正后的功率谱信息′=−σ2，所以全局功率谱模型可进一步简化为

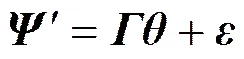
图2 基于全局参考系统的虚拟网络模型

综上所述，全局频谱协作感知算法的核心任务是估计出全局功率谱模型的系数，以求得主用户发射机所使用的频段、功率及其所处位置，其整体流程如图3所示。需要注意的是，由于从用户对主用户的情况一无所知，所以每个从用户必须同时感知所有授权频段。而与传统数据融合方案不同的是，本文的数据融合方案中各从用户发送到融合中心的是其感知到的修正功率谱信息，而不是其接收信号能量信息；融合中心不是对这些信息进行简单加权求和以构成判决统计量，而是直接利用这些信息，构建主用户信号的全局功率谱模型，然后再利用下文所提迭代算法进行求解。而下文所提迭代算法本质上是对各从用户感知信息的一种联合优化，所以其求解出的主用户发射机所使用的频段、功率及其所处位置对于整个认知网络来说是统计意义上最优的。

3 算法描述

变分贝叶斯推断技术是新近出现的一类近似方法，其主要通过观测数据，利用泛函方法近似出复杂的统计模型中不可观测变量的后验概率。因为其采用的也是最大后验估计，即用单个最有可能的参数值来代替完全贝叶斯估计，所以也可以看作是EM算法的扩展。所以其提供的是一种次优，但具有确定解的近似后验估计方法。目前该方法广泛地应用于信号重构、神经元定位等领域[12,13]。本文拟利用该技术设计一种基于变分贝叶斯推断的模型系数求解算法，以给出模型系数的近似后验概率，并利用最大后验概率准则得到模型系数的最优值。

为了表示方便，本文将全局功率谱模型中未知的模型系数向量和模型误差精度参数统一用向量来表示。然后，将全局功率谱模型的对数边缘概率密度函数做如下分解

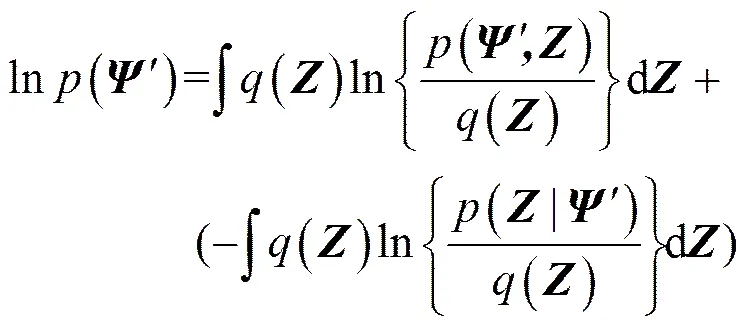
(8)

其中，()表示联合后验概率密度函数(|′)的某种近似，()表示()下的下限，而(||)表示()下的K-L散度。

由于各未知变量和参数互相独立，所以()可以实现因子化，分解为各未知变量和参数的近似后验概率密度函数的乘积，即

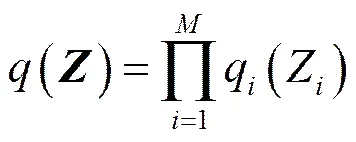
其中，Z表示模型中各未知变量和参数。将式（9）代入()，可得

(10)

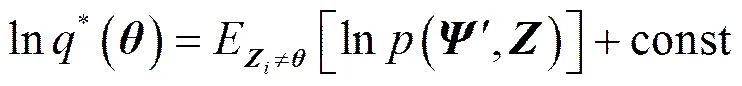
由式（11）可知，求解最优()必须知道模型的联合概率密度函数(′,)，所以如何确定其具体形式成为本文必须首先解决的问题。

由式（7）可知，全局功率谱模型的联合概率密度函数(′,)的具体形式可表示为

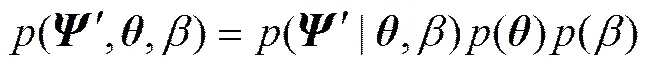
由于模型的误差向量是高斯型噪声，相应协方差矩阵为−1，所以模型的似然函数也是高斯的，具体表达式为

(13)

由此可知，模型系数的共轭先验()也是高斯的，而模型误差精度参数的共轭先验()是伽马分布，因此有

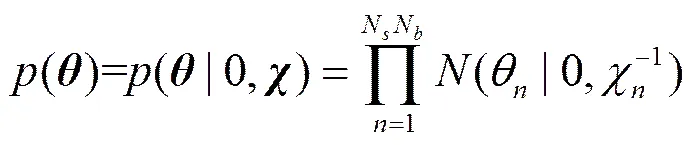
(15)

其中，向量是模型系数的误差精度参数向量；0、0是2个超参数。需注意的是，因为认知网络中存在2种稀疏性：一种是主用户信号占用的频段相对于可利用频谱很窄；另一种是在网络覆盖范围内，存在的主用户数量有限、密度很小。所以模型系数向量也是稀疏的，因此可将式（14）中的均值假设为零向量。

此外，由于也是未知的，所以将向量进一步扩展，加入系数误差精度参数向量，用向量′来表示。则全局功率谱模型的联合概率密度函数(′,)可扩展为(′,′)，其具体形式可表示为

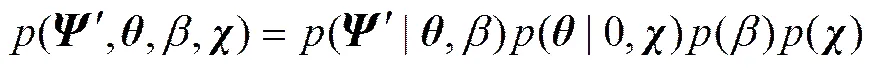
(17)

其中，所有的c、d也都是超参数。由于和以及都是相互独立的，所以式（9）也具体表示为(,)=()()()。由上述可知，()、()和()分别是高斯分布、伽马分布和伽马分布，所以其近似值() 、()和()也应分别是高斯分布、伽马分布和伽马分布，因此有，，。

根据式（11）可得到，()最优值*()的计算式为

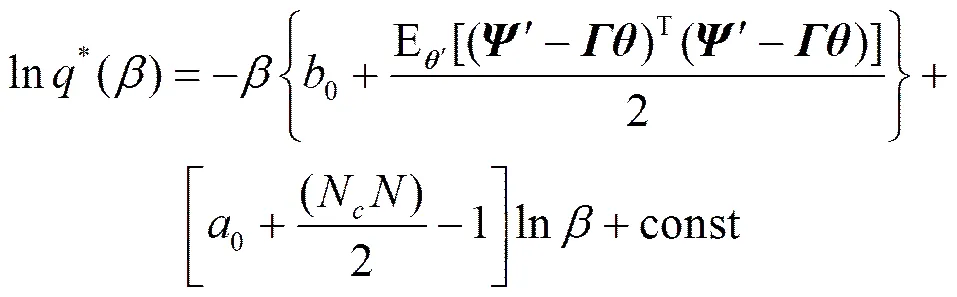
(19)

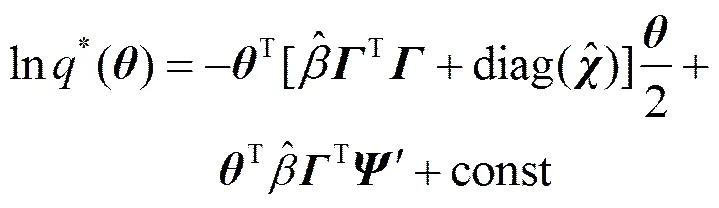
由于该式是高斯分布的对数形式。所以()中的，，其中，的均值，而向量的各元素均值。

由上述公式可知，求解最优()必须依赖其他近似后验()和()，所以在实际使用中，()的最优值难以直接得到，需利用迭代算法进行求解，即每次指定一个近似后验q(Z)，固定其他近似后验为上次计算得到的最优值，利用式（11）求得该q(Z)的本次最优值，如此反复直到得到()的全局最优值，其具体流程如图4所示。

4 仿真结果及分析

本文利用Matlab软件构建了所提方案的仿真平台，并根据基于估计值的真实全局功率谱模型和由式（7）所示的高斯型近似全局功率谱模型分为2种仿真环境，以验证近似模型的准确性和所提算法的有效性。同时本文还比较了2种环境下不同信噪比（SNR, signal noise ratio）时的算法性能，分析了其收敛性，讨论了不同信噪比时估计的准确性和虚假功率泄漏的情况。最后，本文选择了基于非负最小二乘（NNLS, non-negativity least square）准则的全局频谱协作感知算法与所提算法进行了对比，验证了所提算法在均方误差（MSE, mean square error）性能上的优势。

本文仿真条件如下：假设认知网络中存在N=8个连续可用频段，每个可用频段宽度为1 MHz，每个主用户通信占据1个频段，发射功率为1 W。而从用户在感知时扫描的频点数为=64，即从用户在每个可用频段上采样8个点。本仿真中认知网络的参考系统是一个由5×5个点构成的正方形，也就是说认知网络中有N=25个候选位置。而其中假设存在2个主用户，其位置坐标分别为（2，2），（3，5），所占用频段分别为6号频段和7号频段。同时假设存在N=4个从用户，其位置坐标分别为（1，1）、（2，5）、（4，2）、（5，4）。仿真所用的路径损耗相关参数为0=10 m，=4，而参考系统单位坐标代表的实际距离为20 m。由该仿真条件可知，模型系数向量中有N×N=200个元素，但是非零的只有2个，因此系数向量具有较强的稀疏性。而这2个非零元素在向量中的具体位置序号可由主用户的位置坐标和所占用频段换算出来，其换算公式为元素序号=[（横坐标−1）×5+（纵坐标−1）]×8+占用频段号。也就是说，2个非零元素分别在54号和119号位置上，大小为1，所以本文仿真通过考察系数向量的估计精确度来验证算法对主用户发射机所使用频段、功率及其位置的估计能力。

本文先仿真并对比了真实模型和高斯模型2种不同仿真环境下所提算法的性能差异，以验证近似模型的准确性及所提算法的有效性。如图5所示，当系统信噪比=−6 dB时，真实模型下算法的迭代次数为119次，系数向量和其估计值的欧式距离为0.047 1。而在高斯模型下，算法的迭代次数为93次，系数向量和其估计值的欧式距离为0.039，两者差异不大。由此可知，在2种模型下，算法的估计准确度比较接近。这是因为随着增大，估计误差越来越小，也就是误差向量的协方差矩阵中的元素越来越小。这导致2种模型下误差向量的值都主要分布在其均值附近，散布很小，所以此时的2种模型总体上比较接近，因此2种模型下所提算法的性能也比较接近。这一点可由图6进一步证明，当从−10 dB变化到−6 dB时，随着增大，2种模型的吻合程度越来越高，算法性能也越来越接近。尤其是当接收=−6 dB时，两者的均方误差分别是−26.547 8 dB和−28.184 2 dB，仅相差1.6 dB。但是当继续增加时，2种模型下MSE曲线间的差异却仍然保持在1.5 dB左右。这是因为虽然算法泄漏出的虚假功率会随着的下降而减少，但算法在真实环境下总会泄漏出更多的虚假功率。这点可以由图7证明，即当接收=−6 dB时，算法泄漏出的归一化总虚假功率分别为0.028 4和0.011 9，两者相差3.7 dB。而当接收=0 dB时，虽然算法泄漏出的归一化总虚假功率分别下降为0.008 8和0.004 1，但两者仍相差3.3 dB。

本文还仿真并对比了2种仿真环境下不同信噪比时的所提算法性能，并对其收敛性进行了相应分析，同时讨论了不同信噪比时估计的准确性和虚假功率泄漏的情况。由图8可知，当系统信噪比分别等于0 dB、−6 dB和−10 dB时，真实模型下算法的迭代次数分别为91次、119次和129次，系数向量和其估计值的欧式距离分别为0.019 4、0.047 1、0.165 2。而由图9可知，对应的高斯近似模型下算法的迭代次数分别为89次、93次和105次，系数向量和其估计值的欧式距离分别为0.016 1、0.039 0、0.099 7。将上述两图中各迭代次数进行对比可以发现，当由−10 dB变化到0 dB时，2种模型下算法的迭代次数差异都不是很大，也就是说算法的收敛性在2种模型的各种下的稳定性都比较好。但当小于−6 dB时，其估计准确性都开始明显变差。这是因为当变小时，接收的主用户信号功率不变，因此主要是本地噪声功率变大，导致算法的估计准确性明显下降。这点从系数向量的119号元素估计值的准确度也可以看出。例如，真实模型下119号元素估计值在=−10 dB时是0.893 6，在=0 dB时是0.994 7。而高斯近似模型下的估计值在= −10 dB时是0.927 0，在=0 dB时是0.991 9。由此可以明显地看出估计准确性随变小而快速下降。同时将图8和图9进一步对比可知，真实模型下的算法收敛速度在不同信噪比时都要略慢于高斯近似模型下的算法收敛速度，而对应的估计准确性也是高斯近似模型下的准确度都略高于真实模型下的准确度。但两者相差不大，这也再次证明了本文基于高斯近似模型推导出的算法总体上可以较好的适用于真实模型。此外，由图10可知，当系统信噪比分别等于0 dB、−6 dB和−10 dB时，真实模型下算法泄漏出的总虚假功率分别为0.008 8、0.028 4、0.086 7。而由图11可知，对应的高斯近似模型下算法泄漏出的总虚假功率分别为0.004 1、0.011 9、0.033 4。由上述两图可知，的减小不仅影响估计准确度，还导致算法泄漏出的总虚假功率也随之增加。而且由图10可以看到，当=−10 dB时，算法收敛时泄漏出的总虚假功率已经不是其最小值，而是出现了偏离的现象。这是因为较大噪声功率影响了估计的准确性，其收敛值偏离真实值较远，导致泄漏出了更多的总虚假功率。同时将图10和图11进一步对比可知，当接收=−10 dB时，所提算法泄漏出的总虚假功率相差4.1 dB，这再次证明了MSE曲线间存在的差异受到在真实环境下算法泄漏出更多的虚假功率的影响，而这种影响基本不随而变化。

最后，由于传统的协作频谱感知算法仅检测了主用户在授权频段中是否存在，而没有指明主用户所处位置及其发射功率等全局频谱信息，所以难以直接与本文所提算法进行性能对比，为此本文选择了基于NNLS准则的全局频谱协作感知算法与所提算法进行对比。该算法采用的准则为

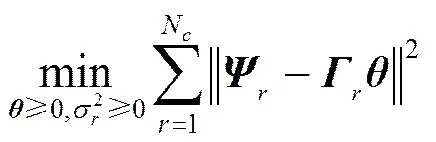
根据利用该准则，本文仿真并对比了在真实模型下NNLS算法和所提算法的MSE性能。如图12所示，当从−10 dB增大到0 dB时，所提算法和NNLS算法的均方误差分别从−15.639 4 dB和9.456 6 dB逐渐减小到−34.232 8 dB和−18.401 0 dB，也就是说两者MSE性能间隔从25.096 dB缩小到15.831 9 dB。由此可见，虽然随着的增加，所提算法的MSE性能领先NNLS算法的程度有所减小，但是仍保持着较大的优势。这是因为所提算法利用了系数向量存在稀疏性这一隐含条件，所以其估计向量中除了54号和119号元素比较接近真实值1外，其他元素估计值都非常接近真实值0。而NNLS算法没有利用这一稀疏性条件，所以其估计向量中除54号和119号元素外，还存在数量较多、数值较大的非零元素，这严重影响了NNLS的估计精度。因此通过该仿真对比，本文证明了利用系数向量稀疏性的所提算法在MSE性能上具有较大的优势，其估计精确度较高，可以通过忽略功率谱模型系数中较小的元素，直接利用较大非零元素来得到主用户发射机所使用的频段、功率及其所处位置的真实值。

图12 本文所提算法和NNLS算法性能对比

5 结束语

首先，本文利用接收到的主用户信号构建了时间域和频率域上的全局功率谱近似模型，并在此基础上设计了一种新型的全局频谱协作感知算法的整体流程。接着，利用认知无线网络中存在的稀疏性，设计了基于变分贝叶斯推断技术的估计器，以求得该模型系数向量的近似后验概率密度函数，从而利用最大后验概率准则得到系数向量的最优值，由此揭示出主用户发射机所使用的频段、功率及其所处位置。最后，本文建立了2种分别基于真实模型和高斯近似模型的仿真环境，以验证近似模型的准确性及所提算法的有效性。同时还比较了2种环境下不同信噪比时的算法性能，分析了其收敛性，讨论了不同信噪比时估计的准确性和虚假功率泄漏的情况。另外，在真实模型下，本文通过将所提算法和NNLS算法的MSE性能进行仿真对比，证明了利用系数向量稀疏性的所提算法在MSE性能上具有较大的优势。

[1] GOLDSMITH A, JAFAR S, MARIC I, et al. Breaking spectrum gridlock with cognitive radios an information theoretic perspective[J]. Proceedings of the IEEE, 2009, 97(5): 894-914.

[2] LU L, ZHOU X W, ONUNKWO U, et al. Ten years of research in spectrum sensing and sharing in cognitive radio[J]. Eurasip Journal on Wireless Communications, 2012, 28: 1-16.

[3] ZENG Y H, LIANG Y C, HOANG A T, et al. A review on spectrum sensing for cognitive radio: challenges and solutions[J]. Eurasip Journal on Advances in Signal Processing, 2010, ID 381465.

[4] NISHIMORI K, TARANTO R D, YOMO H, et al. Spatial opportunity for cognitive radio systems with heterogeneous path loss conditions[C]//IEEE 65th Vehicular Technology Conference VTC.c2007: 2631-2635.

[5] RIIHIJARVI J, MAHONEN P. Exploiting spatial statistics of primary and secondary users towards improved cognitive radio networks[C]// IEEE 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications CrownCom.c2008:1-7.

[6] MIN A W, KIM K H, SINGH J P, et al. Opportunistic spectrum access for mobile cognitive radios[C]//IEEE INFOCOM Conference.c2011: 2993-3001.

[7] CASO G, NARDIS L D, HOLLAND O, et al. Impact of spatio-temporal correlation in cooperative spectrum sensing for mobile cognitive radio networks[C]//The 10th International Symposium on Wireless Communication Systems ISWCS. c2013: 1-5.

[8] PAURA L, SAVOIA R. Mobility-aware sensing enabled capacity in cognitive radio networks[C]//2013 IEEE International Workshop on Measurements and Networking Proceedings M&N.c2013:179-183.

[9] LI F, XU Z B. Sparse bayesian hierarchical prior modeling based cooperative spectrum sensing in wideband cognitive radio networks[J]. IEEE Signal Process Lettes, 2014, 21(5): 586-590.

[10] GIANNAKIS G B, TEPEDELENLIOGLU C. Basis expansion models and diversity techniques for blind identification and equalization of time-varying channels[J]. Proceedings of the IEEE, 1998, 86(10): 1969-1986.

[11] CEVHER V, DUARTE M F, BARANIUK R G. Distributed target localization via spatial sparsity[C]//European Signal Processing Conference EUSIPCO.c2008.:1-5.

[12] GIROLAMI M. A variational method for learning sparse and overcomplete representations[J]. Neural Computation, 2011, 13(11): 2517-2532.

[13] WIPF D, OWEN J, ATTIAS H, et al. Robust Bayesian estimation of the location, orientation, and time course of multiple correlated neural sources using MEG[J]. NeuroImage, 2010, 49(1): 641-655.

Novel cooperative globalspectrum sensing algorithm based on variational Bayesian inference

WU Ming, SONG Tie-cheng, HU Jing, SHEN Lian-feng

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China）

To realize multi-dimensional dynamic spectrum access, an approximate model was proposed for the global power spectral density (PSD) of primary users (PU). Based on the proposed model, a novel cooperative spectrum sensing algorithm was proposed, and its overall flow was also built to obtain global information in the network of PU. The global information included locations, occupied frequency bands and transmitting powers of the PU. Then, an estimator of model coefficient vector was designed by utilizing the theory of variational Bayesian inference (VBI). Simulation results show that the proposed approximate model has good accuracy, and the corresponding estimation algorithm of model coefficient vector has good convergence and stability. Meanwhile, the relationship between SNR and the leakage of aggregate spurious power (LASP) was pointed out, and the influence of SNR and LASP on MSE performance was also discussed. Furthermore, it is proved that the proposed algorithm has better MSE performance than another algorithm since the sparsity of model coefficient vector is utilized.

cognitive radio, cooperative global spectrum sensing, variational Bayesian inference, sparsity

TN914

A

10.11959/j.issn.1000-436x.2016037

2015-04-08；

2015-08-08

国家自然科学基金资助项目（No.61271207, No.61372104, No.61201248）

The National Natural Science Foundation of China (No.61271207, No.61372104, No.61201248)

吴名（1981-），男，江苏南京人，东南大学博士生，主要研究方向为认知无线电系统、协作通信、传感器网络等。

宋铁成（1967-），男，江苏张家港人，博士，东南大学教授、博士生导师，主要研究方向为移动通信理论与技术、认知无线电、物联网等。

胡静（1975-），女，江苏扬州人，博士，东南大学副研究员，主要研究方向为短距离无线通信、泛在网络等。

沈连丰（1952-），男，江苏邳州人，东南大学教授、博士生导师，主要研究方向为宽带移动通信、短距离无线通信与泛在网络等。