Hilbert空间连续K-框架的冗余与扰动性
2016-10-14范丽兰舒志彪
范丽兰, 舒志彪
(福州大学数学与计算机科学学院, 福建 福州 350116)
Hilbert空间连续K-框架的冗余与扰动性
范丽兰, 舒志彪
(福州大学数学与计算机科学学院, 福建 福州350116)
基于连续K-框架的定义, 给出了Hilbert空间连续K-框架的两个等价刻画. 在连续K-框架中挖去部分元素还构成连续K-框架的两个充分条件和不构成连续K-框架的一个充分条件, 利用合成算子和两个连续Bessel映射的有界线性算子SF, G去刻画连续K-框架. 最后讨论Hilbert空间连续K-框架的扰动.
连续K-框架; Hilbert空间; 冗余; 扰动
1 引言
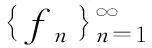
目前学者对连续K-框架研究甚少, 而连续K-框架比K-框架更一般, 因此在K-框架中成立的命题在连续K-框架不一定成立. 所以, 很有必要对连续K-框架进行更深入的研究. 本文讨论了在Hilbert空间连续K-框架的两种等价刻画, 讨论了连续K-框架的扰动和冗余性.
本文采用的记号如下: H表示一个可分复Hilbert空间, Ω表示一个测度空间, 其上的测度记为μ. 对两个Hilbert空间H1, H2, 用L(H1, H2)表示所有H1到H2的有界线性算子的集合. 设T∈L(H1, H2), K∈L(H), 用R(T)表示T的值域, FK(H)表示H中所有连续K-框架集合.
定义1设(Ω,μ)为测度空间, 且μ是σ-有限测度,K∈L(H), 映射F:Ω→H称为H中的连续K-框架, 若满足以下两个条件:
1)F是弱可测的, 即对任意的f∈H,φ:Ω→C,φ(ω)=〈f,F(ω)〉,ω∈Ω,φ是Ω上的可测函数.
2) 存在正数A,B使得
(1)
A, B分别是连续K-框架的下界和上界. 如果(1)式中右边的不等式成立, 则称F为H中的连续Bessel映射, 简称Bessel映射.
注1若有界线性算子K=I, 则连续K-框架就变成了连续框架(见文[5]).
注 2在下文如无特别说明, 都假定K具有闭值域, 因为这样才能保证K+的存在.
本文中还经常用到有界线性算子的伪逆, 为此给出伪逆的定义.
定义2设H1,H2是两个Hilbert空间,Q∈L(H1,H2), 称Q+:H2→H1为Q的伪逆算子, 如果Q+满足QQ+Q=Q. 特别地, 若y∈R(Q), 有QQ+y=y.
引理1[14]设H1,H2为可分Hilbert空间,T1∈L(H1,H2) ,T2∈L(H1,H2). 则下面的论述等价.
1)R(T1)⊂R(T2);
3) 存在有界线性算子X∈L(H1,H2)使得T1=T2X.
2 主要结论
定理1设K1,K2∈L(H), 则当且仅当R(K1)⊃R(K2)时, FK1(H)⊂FK2(H).
证明1) 充分性. 设R(K1)⊃R(K2), 则利用引理1, 可得对∀f∈H有

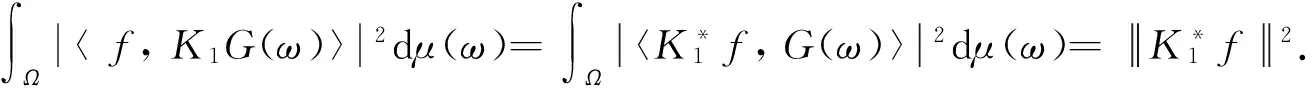
下面的定理比文献[9]中命题2.5更一般, 即当K=I时即命题2.5.
定理2设(Ω,μ)为测度空间, 且μ是σ-有限的,K∈L(H), 则{F(ω)}ω∈Ω⊂H是连续K-框架且界为A,B的充要条件是
(2)
对任意的f∈D都成立, 其中D是H的一个稠密子集.
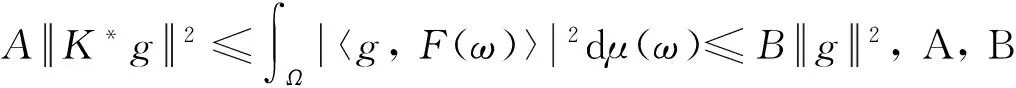
2) 必要性. 先证明F是以B为界的Bessel映射.
那么存在m∈N, 使得
(3)

(4)
两边同时取和可得
(5)
这与式(3)矛盾, 所以F是以B为界的Bessel映射.
下面再证F的下界为A.

(6)
因此
(7)
利用式(6), (7)和三角不等式, 可得
因为ε的任意性, 故结论得证.
接下来讨论Hilbert空间连续K-框架的冗余性, 即在连续K-框架中删除一些元素后是否还构成连续K-框架. 一般情况下, 在连续K-框架的基础上删除某些元素后不能确定是不是连续K-框架. 下面给出删除某些元素后还构成连续K-框架的两个充分条件和一个不构成连续K-框架的一个充分条件.
引理 2[15]设(Ω,μ)为测度空间,μ是σ-有限测度,H是n维的Hilbert空间,F:Ω→H是一个Bessel映射, 则
定理3设(Ω,μ)为测度空间, 且μ是σ-有限测度, {F(ω)}ω∈Ω为n维的Hilbert空间H中的连续K-框架, 且界为A,B. 设ΩI⊂Ω,I是指标集, 且R(K)⊂H是闭的, 则下面的叙述成立.

由此可得
(8)
又{F(ω)}ω∈Ω为H中的连续K-框架, 且界为A,B, 即有
(9)
联合式(8)和(9)得
(10)
另一方面, 设f∈R(K)⊥⊂H, 对任意的g∈H, 有〈K*f,g〉=〈f,Kg〉=0, 所以
(11)


(12)

定义5[9]设(Ω,μ)为测度空间,μ是σ-有限的,F,G是Ω→H的连续Bessel映射, 上界分别为B,D>0, 定义算子
(13)

定理4设(Ω,μ)为测度空间,μ是σ-有限测度,F,G是Ω→H的连续Bessel映射, 且上界分别为B,D>0.
2) 如果存在λ1,λ2∈(-1, 1), 使得
(14)

2) 对∀f∈H, 由式(14)可得

(15)
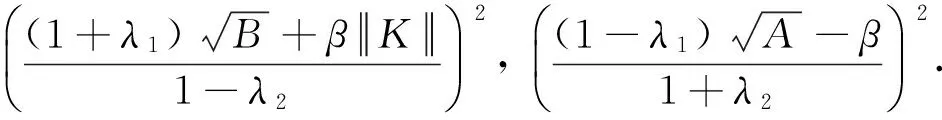
证明由三角不等式和式(15), 对∀f∈H有
所以
同理得
所以
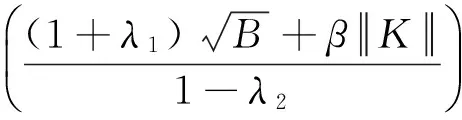
[1]DUFFINRJ,SCHAEFFERAC.AclassofnonharmonicFourierseries[J].TransactionsoftheAmericanMathematicalSociety, 1952, 72(2): 341-366.
[2]DAUBECHIESI,GROSSMANNA.MEYERY.Painlessnonorthogonalexpansions[J].JournalofMathematicalPhysics, 1986, 27(5): 1 271-1 283.
[3]KOVACEVICJ,CHEBIRAA.AnIntroductiontoframes[J].FoundationsandTrendsinSignalProcessing, 2008, 2(1): 1-94.
[4]ALIST,ANTOINEJP,GAZEAUJP.Coherentstates,waveletsandtheirgeneralizations[M].NewYork:Spring-Verlag, 2000.
[5]ALIST,ANTOINEJP,GAZEAUJP.ContinuousframesinHilbertspaces[J].AnnalofPhysics, 1993, 222(1): 1-37.
[6]ASKARI-HEMMATA,DEHGANMA,RSDJABALIPOURM.Generalizedframesandtheirredundancy[J].ProceedingsoftheAmericanMathematicalSociety, 2001, 129(4): 1 143-1 147.
[7]GABARDOJP,HAND.Framesassociatedwithmeasurablespaces[J].AdvancesinComputationalMathematics, 2003, 18(2/4): 127-147.
[8]FORNASIERM,RAUHUTH.Continuousframes,functionspaces,andthediscretizationproblem[J].JournalofFourierAnalysisandApplications, 2005, 11(3): 245-287.
[9]RAHIMIA,NAJATIA,DEHGHANYN.ContinuousframesinHilbertspaces[J].MethodsofFunctionalAnalysisandTopology, 2006, 12(2): 170-182.
[10]AZHIMIA,BEHESHTIM.SomeresultsoncontinuousframesforHilbertspaces[J].InternationalJournalofIndustrialMathematics, 2010, 2(1): 37-42.
[11]GǎVRUTAL.Framesforoperators[J].AppliedandComputationalHarmonicAnalysis, 2012, 32(1): 169-144.
[12]XIAOXC,ZHUYC,GǎVRUTAL.SomepropertiesofK-frames in Hilbert spaces[J]. Results in Mathematics, 2013, 63(3/4): 1 243-1 255.
[13] 丁明玲, 肖祥春, 曾晓明. Hilbert空间中的紧K-框架[J]. 数学学报(中文版), 2013, 56(1): 105-112.
[14] DOUGLAS R G. On majorization, factorization and range inclusion of operators on Hilbert spaces[J]. Proceedings of the American Mathematical Society, 1966, 17(2): 413-415.
[15] GAVRUTA L, GAVRUTA P. Ulam stability problem for frames[J]. Functional Equations in Mathematical Analysis, 2012, 52(2): 139-152.
(责任编辑: 林晓)
Excess and perturbation of continuousK-frames in Hilbert spaces
FAN Lilan, SHU Zhibiao
(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian, 350116, China)
Based on the definition of the continuousK-frames, we propose two kinds of equivalent characterizations for continuousK-frames. We also give two sufficient conditions for the remainder of a continuousK-frame after deleting some elements to be a continuousK-frame and a sufficient condition for the remainder to be not a continuousK-frame. We characterize the continuousK-frames by the synthesis operator and a bounder operatorSF, Gassociated with two continuous Bessel mappings. Finally, we discuss the perturbation of continuousK-frames in Hilbert spaces.
continuousK-frame; Hilbert spaces; excess; perturbation
10.7631/issn.1000-2243.2016.01.0006
1000-2243(2016)01-0006-06
2013-06-11
舒志彪(1958- ), 副教授, 主要从事小波分析、 图像处理、 信息隐藏等方面研究,szb@fzu.edu.cn
福建省自然科学基金资助项目(2012J01005); 国家自然科学基金数学天元基金资助项目(11226099); 福州大学科技发展基金资助项目(2012-XQ-29)
O177.1
A
