一种高清帧内预测单元快速选择算法
2016-10-14黄秋情杨秀芝郑明魁苏凯雄
黄秋情, 杨秀芝, 郑明魁, 苏凯雄
(福州大学物理与信息工程学院, 福建 福州 350116)
一种高清帧内预测单元快速选择算法
黄秋情, 杨秀芝, 郑明魁, 苏凯雄
(福州大学物理与信息工程学院, 福建 福州350116)
针对高效视频编码标准提出一种CU划分快速终止算法. 该算法选择图像纹理复杂度作为特征向量, 将HEVC帧内预测与k-means聚类方法相结合, 通过每种尺寸CU的聚类中心减少率失真优化的次数, 提前终止CU块的划分, 在达到降低编码复杂度的同时依然保持较好的编码效率. 测试结果表明, 本算法与参考算法HM10.0相比较, 视频图像质量基本不变, 而编码时间大幅减少.
高效视频编码标准;k平均算法; 帧内预测; 编码单元
0 引言
2010年1月, ITU-T和ISO/IEC成立JCT-VC(joint collaborative team on video coding)联合组织, 统一制定下一代视频编码标准HEVC(high efficiency video coding)[1-2]. HEVC主要针对高清和超高清视频图像, 其核心目标是在H.264标准的基础上, 把压缩效率提高一倍, 以支持高分辨率视频的压缩. HEVC采用了众多先进的改进和优化的工具, 主要包括更灵活的四叉树图像划分、 扩展的H.264/AVC帧内编码、 改进的运动矢量预测、 新的帧间预测模式-MERGE模式、 帧间预测非对称运动划分四叉树变换、 基于DCT的亚像素滤波器、 新的多参考帧管理方式、 简化的去块滤波(SAO,sample adaptive offset)和高吞吐量的熵编码(CABAC, context-adaptive binary arithmetic coding)等. 这些HEVC众多先进的编码技术能大幅提升视频编码效率, 但也使编码的计算复杂度和编码时间大幅增加. 在实际应用中, 编码速度的提高十分重要. 因此, 如何在保证编码质量不变的情况下降低HEVC的计算复杂度, 加快编码速度, 是推进和扩大HEVC实际应用所要解决的关键问题[3].
传统的HEVC快速算法思想可分为三类: 一是设置阈值提前终止CU块划分,具体表现为可利用当前CU和其四个子块的相关性、 当前CU与相邻CU间的相关性以及图像纹理复杂度等, 预判当前CU是否进行划分, 提高帧内编码速度; 二是 缩小预测模式选择的范围, 具体表现为利用图像处理的算子知识、 精简最有可能模式以及完善粗略模式选择(RMD)算法等, 缩小模式选择的范围, 提高帧内编码速度; 三是简化率失真优化计算. 目前有一种快速算法思想新方向是基于机器学习的思想, 例如文献[4]利用以CU纹理复杂度为特征向量的k-means聚类方法对CU逐层分析划分与否, 同时为了进一步减少编码时间提出基于像素方差阈值的快速CU单元选择. 文献[5]利用贝叶斯分类思想和支持向量机对CU是否划分做出快速判断, 通过统计各种类别的先验概率, 计算其后验概率, 然后根据最小经验风险进行分类.
基于k-means的快速算法与贝叶斯分类思想以及支持向量机的方法比较,k-means思路相对简单、 步骤简练、 结果准确. 但现有k-means方法[4]仍然存在许多不足, 其中最为突出的一点是将k-means完全替代率失真代价计算, 这种方法将图像纹理复杂度作为CU是否划分的唯一依据, 完全忽视了SAD计算、 SATD计算等其他因素的影响, 这势必产生较大的性能损失.
本研究利用k-means聚类算法的思想, 选择图像纹理复杂度作为特征向量, 对HEVC帧内预测算法进行改进. 将HM10.0最优划分CU的方差作为输入向量, 离线训练64×64、 32×32、 16×16和8×8 CU尺寸四种聚类中心, 获得CU尺寸与方差之间相关性的经验值, 最终与RDO(rate distortion optimization)计算相结合, 减少循环计算次数以达到降低编码复杂度的目的. 结果表明, 该快速算法能在保证视频图像质量几乎不变的情况下, 降低大量帧内预测时间.
1 图像纹理复杂度与CU分块的关系
对于视频图像, 通常使用小尺寸的CU块编码纹理复杂的区域, 而使用较大尺寸的CU块编码纹理相对简单的区域[6-7], 序列BasketballDrill第一帧编码(QP=32)时, CU划分如图1所示.
由图1可得, 地面等区域, 基本都采用了64×64和32×32 的大尺寸 CU 块进行编码, 这些区域通常图像平坦, 像素间差异也较小; 与此相反, 篮筐、 人物等具有细节丰富且像素间差异较大特点的区域, 则基本选用了 16×16 和 8×8的小尺寸 CU 块进行编码. 因此可认为, 纹理复杂度与CU尺寸有密切的关系. 本研究使用方差表示像素间的差异, 进而表示图像纹理复杂度. 算法定义方差表示为δM×N. Pel(i,j)表示图像坐标位置(i,j)上的像素值, Mean表示图像的平均像素值,M和N表示图像的长和宽,M、N=8、 16、 32和64.
(1)
(2)
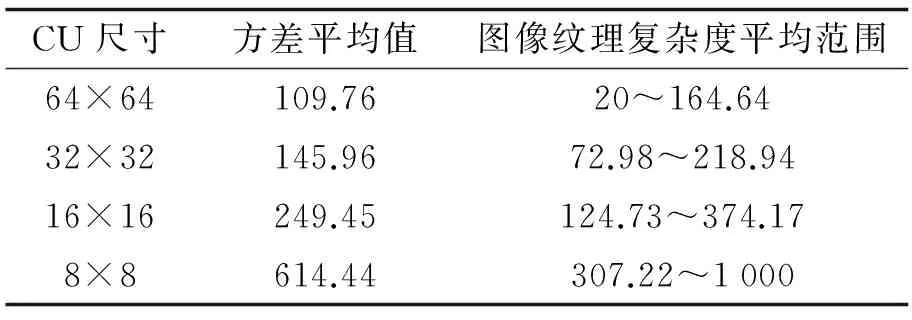
表1 CU方差平均范围Tab.1 CU mean variance
为了分析方差与LCU分块之间的关系, 选取多个测试序列[8]进行实验. 使用HM10.0对序列进行帧内预测编码, 将经率失真代价计算得到的所有LCU最优划分结果与其对应的方差进行比较, 如表1所示. 由表1可得, 方差平均值与CU尺寸成反比关系, CU尺寸越小, 方差越大. 反之, 若求出一个较大的方差值, 则该CU很可能被划分成小尺寸CU. 因此, 使用方差的特征可以较大程度上判别CU分块的尺寸.
2 基于k-means聚类算法的视频方差特征离线训练
现有k-means算法[4]认为, 当前CU是否进一步划分与子块方差有关. 使用4个子块复杂度构成四维输入向量, 每个64×64、 32×32和16×16块都对应一个四维向量, 每个块的划分情况都有划分和不划分两种, 离线训练两种聚类中心如表2所示. 通过判断待预测CU分别与两个聚类中心的最小距离, 得出该CU是否需要进一步划分的结论.
“好战的国王”是“文字的嘲弄者”,也是“灰色真理”和世界“不安”的始作俑者。世界的不安是因为人性的堕落和当时处于殖民统治下的多难爱尔兰的写照。接下来的第二节告诉我们:“故崇拜如尘之举不聪明,/也别试图——因这也是真实——/去千方百计地渴求真理,/以免你所有辛劳只催生/新梦,新梦;世上没有真理,/除了在你自己的心里”(ibid.)。牧羊人要世人不要“崇拜如尘之举”,也不要“千方百计地渴求真理”,因为这样只会在新的幻梦里催生更多的堕落。牧羊人道出了一个真相:真理只存在于“你”的内心。这个“你”是牧羊人,是读者,也是包括诗人在内的艺术家。

表2 文献[4]算法CU聚类中心Tab.2 CU cluster center for reference[4]
现有算法在CU划分过程中未进行率失真代价判断, 减少大量循环计算的时间, 降低编码复杂度, 但CU的正确划分与多种因素有关, 仅使用经验值和先验概率的方法将导致性能上损失较大, 同时, 使用四维向量进行分类增加了判断的难度.
针对这一缺点进行改进, 使用所有最优划分CU的方差作为输入向量. 从上一节实验统计结果可知, 同一尺寸CU的方差值较为接近, 不同尺寸CU的方差平均值相差较大, 因此, 可以直接使用各层的方差以一维向量形式进行聚类分析. 由于将图像纹理复杂度作为唯一的划分依据可能产生性能损失, 本研究在近似判断划分范围的基础上保留率失真代价计算, 在减少部分循环计算时间的同时也保证了编码性能.
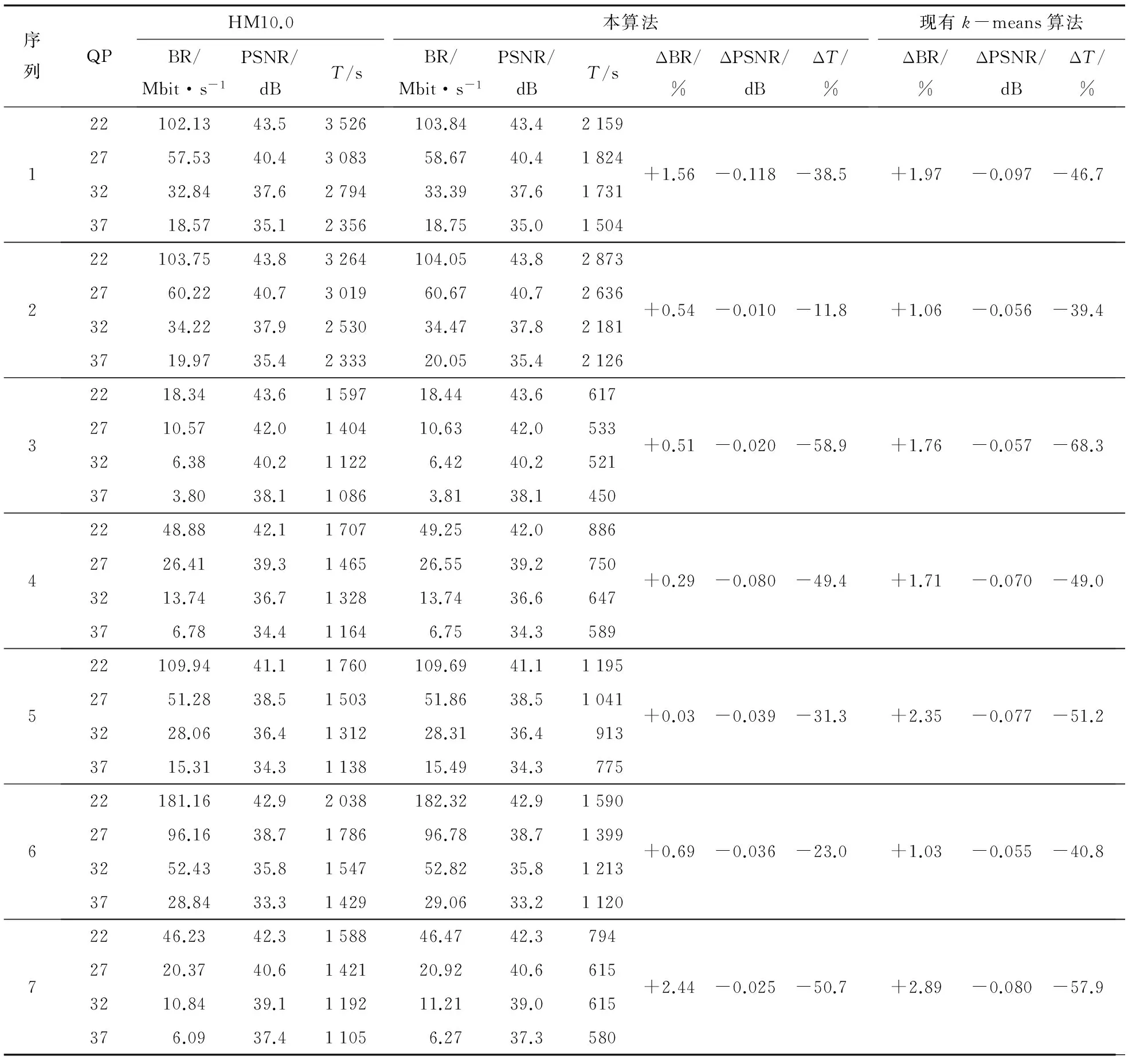
基于以上考虑, 在测试序列帧内编码后得到大量的方差, 为了得到不同尺寸CU与方差大小的对应关系, 利用k-means算法对这些方差进行分类.k-means聚类算法是一种高效的分类器, 也被称为k-平均, 它的目标是将n个输入向量分类到k(k (3) 其中: μi是每个聚类的中心点, xj是每个聚类中输入向量的索引值. k-means聚类的计算过程是一个迭代的过程[11], 具体过程如图2所示. 具体描述如下: 1) 选取比特深度为8的不同分辨率大小的测试序列, 获得测试序列按HEVC原有算法计算的CU最佳划分尺寸以及最优划分CU块的方差, 将这些方差作为输入向量. 2) CU最优划分的依据是RDO计算, 一个CU块有可能大部分平坦而有很小一块区域复杂, 但因RDO计算无需进一步划分, 此时该CU块的像素方差较同尺寸CU的平均情况而言会有极大的偏差, 因此需要计算每个尺寸CU块可用的图像纹理复杂度的平均范围. 另外,k-means算法对噪声和孤立点非常敏感, 因此, 在训练过程中去除复杂度小于20和大于1 000的数据. 3) 从剩下的可用数据中随机选择4个作为聚类的初始中心点. 5) 使用每个聚类中数据的均值作为新的聚类中心点, 重复执行步骤4), 直到两次迭代得到的聚类中心点一致. 利用Matlab软件进行多次离线训练以确保结果稳定可靠, 最后离线训练得出4个聚类中心, 如表3所示. 表3 CU聚类中心Tab.3 CU cluster centers 现有k-means方法[4]将当前CU的4个子块方差作为k-means算法的输入向量, 离线训练划分与不划分两种聚类中心, 最终通过比较两种尺寸方差之间的关系判断当前CU是否需要进一步划分. 该算法虽然能大量降低编码时间, 但由于其将k-means算法完全替代RDO计算, 会导致编码性能损失较严重. 本算法针对该算法的不足之处进行改进研究, 与该算法相比, 本算法先验证方差与LCU分块之间的关系, 获取不同分辨率大小的测试序列在HM10.0最优划分情况下的CU方差. 将这些方差都作为输入向量, 利用k-means算法聚类得到不同尺寸CU与方差大小的对应关系, 离线训练得到4种聚类中心(64×64、 32×32、 16×16和8×8), 获得CU尺寸与方差之间相关性的经验值. 由于图像纹理复杂度并不能作为CU是否划分的唯一标准, 因此将k-means算法与RDO计算相结合, 减少RDO循环计算次数, 该方法能在大量降低编码时间的同时更好地保证编码性能. 本算法流程分析如下, 流程图如图3所示. 1) 计算各尺寸CU的图像纹理复杂度. HM10.0对测试序列进行最优划分处理, 得出若干个8×8、16×16、32×32和64×64CU, 分别统计这些尺寸CU的方差; 2) 利用MATLAB计算各聚类中心. 由于k-means算法对噪声和孤立点非常敏感, 因此去除较方差平均值有极大偏差的数据以及复杂度小于20和大于1 000的数据; 3) 开始64×64尺寸的LCU块划分选择过程; 4) 计算当前LCU块的图像纹理复杂度; 5) 根据欧式距离对LCU的图像纹理复杂度进行分类. 由于前文验证方差与CU尺寸的对应关系并已获得8×8、 16×16、 32×32和64×64CU方差对应的聚类中心, 因此若当前LCU方差与其中某个聚类中心满足最小距离原则, 就可近似认为当前LCU可照聚类情况划分; 6) 根据分类结果对LCU进行前k次块划分选择. 由于图像纹理复杂度并不能作为CU是否划分的唯一标准, 因此本文将k-means算法与RDO计算相结合. 利用方差得出CU划分最可能的范围, 再在这个范围内进行RDO计算, 减少较多复杂的循环运算; 7) 完成64×64尺寸的LCU块划分选择过程. 本算法在HEVC编码标准参考代码HM10.0上进行试验, 亮度LCU大小为64×64, 最大深度为4, 测试配置以HEVC编码通用测试条件[8]为基础, 只对全I帧(AI, all intra)配置进行测试, 使用2个2 560×1 600(Traffic、 PeopleOnStreet)和5个1 920×1 080(Kimono1、 ParkScene、 Cactus、 BQTerrace、 BasketballDrive)大分辨率序列, 以上7个序列按Traffic、 PeopleOnStreet、 Kimono1、 ParkScene、 Cactus、 BQTerrace、 BasketballDrive顺序进行测试. 这些序列都具有不同特点: Traffic和PeopleOnStreet序列由多个运动缓慢物体组成, Kimono1序列由纹理复杂度高的背景组成, ParkScene序列由纹理复杂度高的运动物体组成, Cactus序列包含多种运动方式, BQTerrace序列中既有复杂纹理区域又有简单纹理区域, BasketballDrive序列由运动剧烈物体组成. 本次试验使用的量化参数QP(quantizer parameter)为22, 27, 32和37. 使用ΔPSNR和ΔBR来表示算法性能、 ΔT表示算法复杂度. 其中, 正值的ΔBR或负值的ΔPSNR表示本算法率失真性能损失, 负值的ΔT表示本算法复杂度降低. 实验结果如表4、 表5所示. 表4 不同QP下, HM10.0以及现有k-means算法[4]与本算法结果对比Tab.4 HM10.0 and existing k-means algorithm[4] comparison with the results of this algorithm under different QP (4) (5) (6) 从表4和表5可以得出, 相比于HM10.0, 本算法平均减少37.8%的编码时间, 编码性能几乎相同, 其中有0.87%BR增加和0.047 dB的PSNR减少. 本算法由于进行大量离线训练, 获得CU尺寸与方差之间相关性的经验值, 减少RDO循环计算次数, 大量降低编码时间. 其中, Kimonol序列效果最为明显, 这是由于该序列背景纹理复杂度极高, 方差与CU分块关系较其他序列更为密切; 而PeopleOnStreet序列效果不太明显, 这是由于该序列中有多个运动缓慢的物体, 整个序列纹理复杂度较低, 方差大小在CU是否分块的判断中只占很小部分. 同时, 与现有k-means算法相比, 考虑到图像纹理复杂度并不能作为CU是否划分的唯一依据, 本算法只是将k-means算法与RDO计算相结合, 在减少编码时间的前提下, 更好地保证编码性能, 从而改进现有k-means算法[4]在性能方面的缺陷, 性能损失减少一个百分点. 表5 优化对比Tab.5 Optimize contrast 将本算法测试所得的序列率失真性能与HM10.0的比较, 如图4所示. 从图4中可以看到, 所有序列的曲线几乎重叠, 这进一步说明了本算法能保持与HM10.0基本相同的率失真性能. 针对在保证HEVC编码性能的基础上, 减少HEVC编码时间的问题, 提出一种HEVC帧内编码单元快速划分算法. 该算法以图像纹理复杂度为特征, 选择最佳尺寸CU的方差作为一维输入向量, 通过k-means聚类算法离线训练得出4层CU尺寸对应的聚类中心, 以此为基础判断并排除多余的模式选择过程, 减少RDO循环计算次数. 由于帧内预测中的计算复杂度主要取决于RDO迭代运算, 减少RDO循环计算次数可极大提高HEVC编码速度. 考虑到CU是否划分是由多种因素共同决定, 为降低将图像纹理复杂度视为唯一划分依据可能产生的性能损失, 只将k-means聚类结果视为一个最为可能的值, 在可能的划分范围内仍进行基于RDO模式选择, 在达到降低编码复杂度的同时依然保持较好的编码性能. 实验采用ΔPSNR和ΔBR表示算法性能、 ΔT表示编码时间, 与现有k-means算法[4]相比, 改进了其性能损失过多的不足; 与参考算法HM10.0相比, 能够平均减少37.75%的编码时间, 同时保持与参考算法几乎相同的率失真性能. [1] OHM J R, SULLIVAN G J. High efficiency video coding: the next frontier in video compression standards in a nutshell[J].IEEE Signal Processing Magazine, 2013, 30(1): 152-158. [2] SULLIVAN G J, OHM J R, HAN W J,etal. Overview of the high efficiency video coding (HEVC)standard[J]. Circuits and Systems for Video Technology, 2012, 22(12): 1 649-1 668. [3] BOSSEN F, BROSS B, SUHRING K,etal. HEVC complexity and implementation analysis[J]. Circuits and Systems for Video Technology, 2012, 22(12): 1 685-1 696. [4] 周承涛. HEVC编码快速算法关键技术研究[D]. 杭州: 浙江大学, 2014. [5] 沈晓琳. HEVC低复杂度编码优化算法研究[D]. 杭州: 浙江大学, 2013. [6] 蒋洁, 郭宝龙, 莫玮, 等. 利用平滑区域检测的HEVC帧内编码快速算法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(3): 194-200. [7] 姬瑞旭. HEVC帧内模式决策和CU划分快速算法[D]. 西安: 西安电子科技大学, 2014. [8] BOSSEN F. Common test conditions and software reference configurations[C]// Proceeding of the JCT-VC 10thMeeting. Stockholm: [s.n.], 2012. [9] WU J J, LIU H F, XIONG H,etal.k-means-based consensus clustering: a unified view[J]. IEEE Transactions on Knowledge and Data Engineering, 2015, 27(1): 155-169. [10] GARCIA M L, RICARDO G R, GOMEZ A G.K-means algorithms for functional data[J]. Neurocomputing, 2015, 151(1): 231-245. [11] MALINEN M, FRANTI P.K-means: clustering by gradual data transformation[J]. Pattern Recognition, 2014, 47(10): 3 376-3 386. (责任编辑: 沈芸) A kind of high definition intra-prediction unit fast selection algorithm HUANG Qiuqing, YANG Xiuzhi, ZHENG Mingkui, SU Kaixiong (College of Physics and Information Engineering, Fuzhou University, Fuzhou, Fujian 350116, China) We proposed a CU fast selection algorithm for high efficiency video coding standard, we select the image texture complexity as the feature vector, combined the HEVC intra prediction withk-means clustering method, reduce times of the CU rate distortion optimization sizes and make early divided termination of CU blocks by each cluster centers, reduce coding complexity while still maintaining good coding efficiency. The test results show that the algorithm is compared with the reference algorithm HM10.0, video quality will remain basically unchanged, while significantly reducing encoding time. high efficiency video coding;k-means; intra-prediction; coding unit 10.7631/issn.1000-2243.2016.01.0057 1000-2243(2016)01-0057-07 2015-07-31 杨秀芝(1963-), 教授, 主要从事电子信息工程研究, yangxz@fzu.edu.cn 福建省科技重大专项基金资助项目(2014HZ0003-3); 福建省自然科学基金资助项目(2015J01251); 福建省教育厅科研资助项目(JA14065) TN941.3 A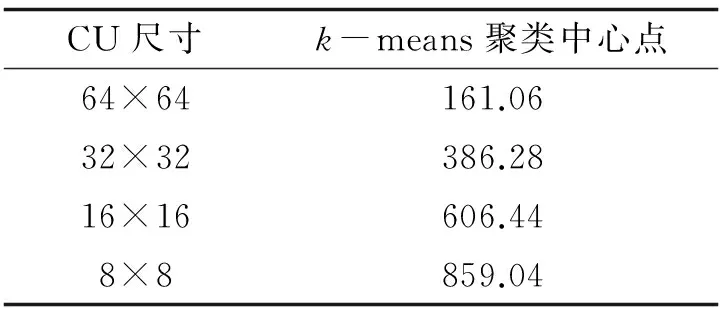
3 CU快速选择算法实现
4 实验结果与分析

5 结语
