基于非完全信息博弈竞标的无线传感器网络资源分配方法

张顺华， 刘漳辉, 2

(1. 福州大学数学与计算机科学学院， 福建 福州　350116; 2. 福建省网络计算与智能信息处理重点实验室， 福建 福州　350116)



基于非完全信息博弈竞标的无线传感器网络资源分配方法

张顺华1， 刘漳辉1, 2

(1. 福州大学数学与计算机科学学院， 福建 福州350116; 2. 福建省网络计算与智能信息处理重点实验室， 福建 福州350116)

针对无线传感器网络任务调度过程中造成的资源冲突问题， 将其考虑为节点间的非完全信息博弈竞标过程； 在参与竞标的节点进行决策时， 引入隐马尔可夫链预测其他竞争者的决策， 将资源分配过程中的多个优化目标， 分别由任务和节点进行优化， 并提出一种非完全信息博弈竞标算法； 在假设节点个人理性的前提条件下， 论证此非完全信息博弈竞标模型满足经济学原理中的激励相容性和最大化系统收益. 最后并从实验仿真证明其有效性.

无线传感器网络； 资源分配； 竞标； 博弈

0　引言

考虑到传感器节点的异构性和动态性， 近几年越来越多的学者研究结合经济学原理进行资源分配， 如分配过程中引入效益函数， 在自适应分配方法中将节点与任务虚拟成虚拟市场中的买家和卖家等等， 并取得了较好的成果. 如文献[1-4]提出一种基于市场机制的资源分配算法， 该算法实现自主分配无线传感器网络中的稀有资源， 以实现能量均衡和最大化网络生命周期. 文献[5-8]提出一种基于组合拍卖机制的无线传感器网络任务调度算法， 通过市场机制调节资源间的合作以提高网络的生命周期， 能有效实现传感器资源的动态分配. 文献[9-10]提出新的基于组合双向拍卖的资源分配模型. 前面文献中提出的市场模型和组合拍卖模型在竞标过程中只考虑到节点与任务之间的关系， 而忽略了节点与竞争节点间的关系， 缺乏对整体信息的利用， 如应用于现实场景， 很难做出最优决策. 文献[11]将博弈理论应用到资源分配中， 并论证资源分配博弈中Nash均衡点的存在性和唯一性以及Nash均衡解. 文献[12]将正比例资源共享的网格环境中多用户竞争同一计算资源问题形式化为一个多人序贯博弈， 在节点的决策过程中， 将前轮博弈结果作为下次博弈的预测， 相当于对整体信息的利用. 文献[13]针对网格计算环境动态、 异构和分布的特性以及网格资源分配中资源利用率低、 效益不均等问题， 结合微观经济学理论， 把资源分配看作一场非完全信息博弈过程， 在实验部分证明比文献[12]更优.

考虑到无线传感器网络与网格特征的相似性、 同为异构性、 动态性， 借鉴文献[13]中的模型， 提出一种非完全信息博弈竞标模型(non-complete information game bidding model, NCIGBM)应用于无线传感器网络资源分配. 针对无线传感器网络资源的特征， 构造相应的效用函数， 并在以节点个人理性的前提条件下， 从理论上论证了此模型满足经济学原理中的激励相容性和最大化整体收益， 最后也从实验仿真部分验证其有效性.

1　资源分配问题描述

假设一个无线传感器网络由m个传感器组成， 有n个独立任务要竞争使用传感器， 则资源管理的目标就是合理地把传感器资源分配给n个任务， 使任务的总完成时间最小， 传感器上所消耗的能量最小， 传感器能量均衡率最大. 任务在各传感器上的执行时间可以根据任务类型通过预测技术和实际历史处理来预测估计， 具体的估计执行时间可以用一个n×m的矩阵consume来表示， 其中的元素consumeij表示任务i在传感器j上的估计执行时间. 传感器Sj的执行时间为分配到该传感器上的所有任务执行时间之和， 具体表示如下：

(1)

由于各节点是并行工作， 因此所有任务的完成时间为节点中最大执行时间， 具体表示如下：

(2)

无线传感器网络完成时间描述了任务被分配到最佳或近佳传感器的程度， 它的值越小， 表示有越多的任务被分配到比较理想的传感器上运行， 可表示为：

(3)

此外， 传感器在处理任务中能量消耗可表示为：

(4)

pcost为节点的单位时间所需能耗， 则传感器的总能量消耗可表示为：

(5)

一个好的分配调度算法除了要保证传感器网络的总完成时间尽量短和所消耗的总能量尽可能少的同时， 还要保证传感器网络的能量平衡. 能量均衡率越高， 网络的生命周期越长， 能量均衡率可表示为：

(6)

式中: GAPmax=max{UEi}-min{UEi}， gapj=max{UEj}-UEj

综上， 传感器资源管理是一个多目标优化问题， 其数学模型表示为：

maxLP

minUT,TE

式中: UT， TE， LP如公式(2)、 (5)、 (6)定义， 如果任务i分配给j则xij=1， 否则xij=0.

2　非完全信息博弈竞标模型

2.1NCIGBM的结构

在无线传感器网络中， 任务是实时的、 动态的， 这是一个不确定的过程， 而每当有任务到来， 会有很多节点同时满足任务的要求， 会造成资源间的冲突. 应用经济学原理的观点， 这其实是一个博弈竞标的过程. 各节点为博弈的参与者， 节点根据自身的状态、 自身与任务的关系以及对竞争节点决策的预测， 做出最优决策; 在所有竞标者都提交竞标价后， 任务再根据自身的收益函数选择最优节点， 并将任务分配给竞标胜节点. NCIGBM结构主要由三部分组成： 任务管理模块、 竞标管理模块和节点管理模块， 如图1所示.

2.2非完全信息博弈竞标机制

由上节可知， 无线传感网络资源分配为一多目标优化问题， 其优化目标为任务的总执行时间、 节点总消耗能量和各节点能量均衡率. 文中主要考虑任务Agent和节点Agent， 其中目标任务的总执行时间交由任务Agent优化， 节点总消耗能量和节点能量均衡率作为节点Agent的优化目标. 非完全信息博弈竞标机制主要包括发标、 竞标、 评标和中标四个过程， 图2为非完全信息博弈竞标机制流程图.

1) 发标和竞标. 当任务到来时， 任务会将其需求提交至发标模块， 然后发标模块将此需求封装成消息广播至各节点. 而此时网络中会有很多传感器节点同时满足需求， 这时就会产生一个资源冲突问题， 如将传感器节点看成智能个体， 则冲突问题可以看成是竞争问题. 又因为传感器节点间信息了解的不全面性， 所以将节点间的竞标考虑为非完全信息博弈过程， 节点为博弈的参与者， 其主要问题是如何做出最优决策以使自身的收益最大. 这里节点的决策以竞标价的形式给出， 结合博弈理论及现实生活中竞标过程， 竞标者在做决策时会考虑自身与任务之间的关系， 自身与竞争者之间的关系， 而自身与任务之间的关系为已知条件. 所以, 主要是如何精确估计竞争者的决策， 以确定自身与竞争者之间的关系. 在此, 本文引入隐马尔可夫模型预测竞争者的决策.

当节点接收到发标模块广播的招标消息时， 节点会检查自身状态是否满足任务需求， 如不满足， 则不参与竞标; 如满足， 则首先对任务需求生成价值估计， 用Vij表示， 此值也体现节点的偏好. 再结合其自身状态、 竞争者历史竞标信息和全局信息， 使用隐马尔可夫模型预测此轮其他竞争者的策略， 然后得出本轮竞标胜的概率， 用Pij表示. 假设将竞标者的最优决策用GVij表示， 则竞标者的收益可表示为:

隐马尔可夫模型(HMM)包括隐含状态集(S)、 可观测状态集(O)、 初始状态概率矩阵(π) 、 隐含状态转移概率矩阵(A)和观测状态转移概率矩阵(B)五个元素.

竞标初期， 为每个节点生成一条隐马尔可夫链， 其中各任务在各个节点上执行所需要的能量为共同知识， 以各个任务在节点i上执行所需能量作为节点i的HMM中的可观测状态Y， 以竞标者的单位出价为隐含状态， 其中A, B元素随机分布于区间(0, 1)， 并保证∑πi=1， ∑jAij=1和∑jBij=1.

利用Baum-Welch算法训练出最优参数{π， A, B}通过Viterbi算法求出对于每个可观测状态对应的最大概率的隐含状态. 在每轮竞标过程中， 竞标者利用全局信息和历史信息， 再通过隐马尔可夫链对竞争者的单位出价进行预测， 然后推算出本轮胜标的概率， 可表示为：

式中： PB数组为节点对任务的单位竞标价.

假设各竞标节点都为理性节点， 即以最大化自身利益为目标， 竞标者为了达到最高收益， 计算E’=0, 最后可求得

(7)

式中:A=Rij×W,Rij为任务i在节点j上执行所需时间，W为其他竞争者预测竞标单价之和;V代表的是竞标者与任务之间的关系， 也体现了竞标者自身的状态；A代表竞标者与其他竞标之间的关系， 即竞标者与竞标者之间的关系， 也就是个体与整体的关系.

竞标者节点对任务的真实估价Vij， 可表示为：

(8)

2) 评标和中标. 在每轮竞标结束后， 竞标模块会将接收到的竞标price集合传给评标模块， 而评标模块会根据任务的偏好和提交的竞标价择出最优竞标者. 对于任务而言， 偏好于执行时间短和可靠性高， 这里的可靠性理解为节点剩余能量多. 从节点的效用函数可以看出， 节点的剩余能量越多， 竞价越高. 因此可将任务的偏好， 即效用函数表示为:

(9)

式中:Tij为任务i在节点j上预计的执行时间， 然后评标模块计算任务对各竞标节点的偏好值， 并按从大到小排序， 并选出最大值作为本轮的竞标胜者. 最后把竞标胜者传送给中标模块， 中标模块再将此消息传给相应的任务和广播给各节点， 节点接收到广播消息后, 如消息中的竞标胜者为自身， 则将任务列入自己的待执行任务列表， 并调整状态； 如不是， 则不作任何变化.

2.3NCIGBM的主要算法

非完全信息博弈竞标模型中主要算法步骤如下：

输入： 任务对传感器节点的需求矩阵consume数组, 节点单位时间所需能耗pcost数组, 节点对任务的竞标价price数组, 权值系数a，b，c，d.

输出： 任务的分配结果result数组.

步骤1初始化consume， pcost， price，a，b，c，d， result;

步骤2训练每个节点i的隐马尔可夫链;

步骤2.1通过HMM算法为节点i生成一条隐马尔可夫链;

步骤2.2通过Baum-Welch算法为节点i训练处最优参数{π，A,B};

步骤2.3通过Viterbi算法求出对于每个可观测状态对应的最大概率的隐含状态;

步骤3计算任务i的最优节点， 对于每个节点j;

步骤3.1判断节点j是否能满足任务i的需求， 如不满足则跳到步骤3， 如满足则转到3.2;

步骤3.2计算各竞争者的最大可能竞标单价之和W;

步骤3.3根据公式(8)求出Vij， 根据公式(7)求出GVij;

步骤3.4根据Vij和GVij+求出竞标价priceij;

步骤4将本轮各参与者提交的竞标价传给评标模块;

步骤5对每个节点根据公式(9)计算Eij;

步骤6选出最大Eij为竞标胜节点， 将此消息通知给任务并广播给各节点， 调整竞标胜节点状态.

4　性能分析

NCIGBM是无线传感器网络中以经济学理论为依托的模型， 本节将从激励相容和系统收益两个方面分析证明其效用.

2)最大化系统收益. 在无线传感器网络中， 系统收益为任务收益和节点收益之和， 假设系统总收益用E表示， 任务收益用TE表示， 节点收益用NE表示， 则E可表示为：

因为在竞标过程中， 节点总是最大化自身收益， 因此priceij为节点的最优值， 而在评标阶段， 任务是选取log(priceij/consumeij)值最大的作为胜标节点， 因此也为最优值. 综上， 在节点和任务都最大化自身收益的同时， 系统收益也最大化.

5　实验仿真

模拟实验选取GREED、 IPSO算法[14]和SMM算法[15]进行横向比较, 比较的主要性能指标有总执行时间、 总消耗能量和节点的能量均衡率.

5.1参数设置

由于现实生活中无线传感器网络大多为异构网络， 为了满足异构性， 本文将参数设置如下： 传感器节点随机分布在100 m×100 m的环境中， 任务对各资源节点的需求consume随机分布于[1 s, 10 s]， 值越大表示任务在此传感器节点上执行所需的时间越长， 节点的单位时间所需能耗随机分布于(0 MJ/s, 1 MJ/s]， 值越大表示节点执行单位时间需消耗的能量越多， 节点的初始能量值随机分布于[30 MJ, 50 MJ]， 对于节点效用函数参数β设为20，α设为0.9. 节点数和任务数值的设定分为5种情况： 节点数远少于任务数、 节点数略少于任务数、 节点数等于任务数、 节点数略大于任务数和节点数远大于任务数.

5.2实验分析

分别选取以能耗为贪心原则的GREED、 IPSO和SMM进行对比， 实验结果如表1和图3所示.

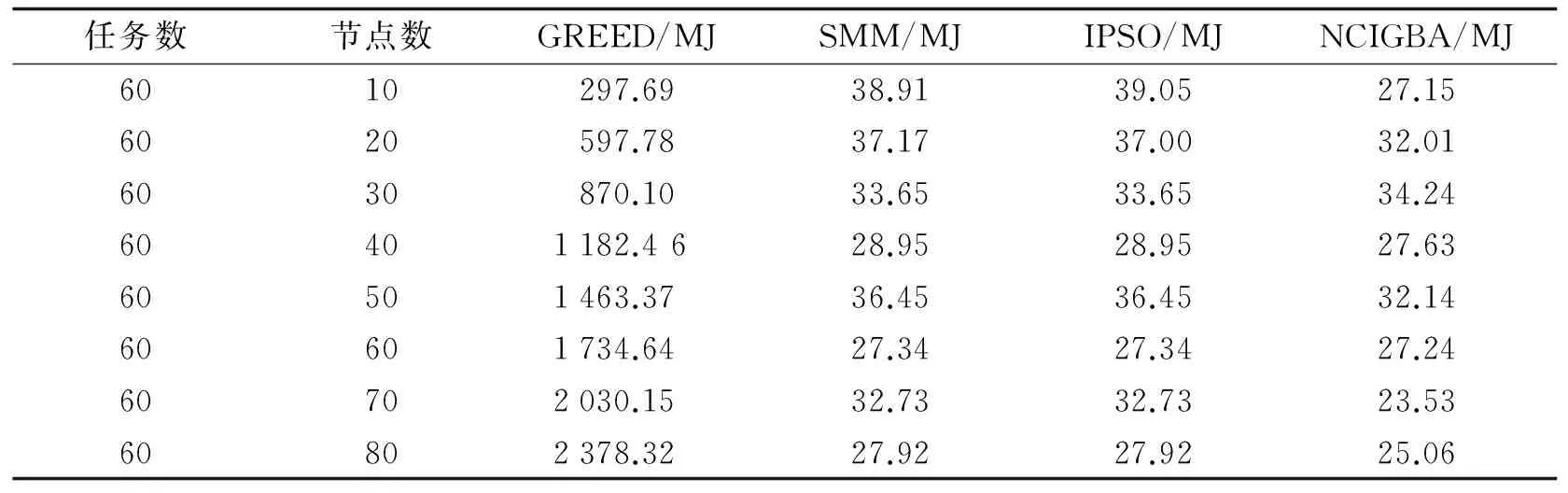
表1　GREED、 SMM、 IPSO和NCIGBA总消耗能量Tab.1　The total energy consumption of GREED、 SMM、 IPSO and NCIGBA

从表1可以看出， 随着节点数的增加， GREED算法得出的总消耗能量逐渐增加， 而SMM、 IPSO和NCIGBA得出的总消耗能量总体呈下降趋势， 因为随着节点数的增多， 任务的可选节点增多， 故能得到更优的分配. 对比SMM、 IPSO和NCIGBA的总消耗能量， 当节点数远小于任务数时， IPSO得出的总消耗能量低于SMM得出的总消耗能量; 随着节点数的增多， IPSO得到的总消耗能量逐渐与SMM得到的总消耗能量相同， 8组数据中， NCIGBA得出总消耗能量一直低于GREED、 SMM和IPSO得出的总消耗能量.

从图3(a)中可以看出， 总执行时间性能指标随着节点数的增加， NCIGBA、 IPSO和SMM得到的总执行时间慢慢减少， 并逐渐趋于稳定， 而GREED得到的总执行时间变化较大， 并远远大于NCIGBA、 IPSO和SMM得到的. 在节点数较少的时候， SMM得到的总执行时间略大于IPSO， 都大于NCIGBA， 随着节点数的增加， NCIGBA、 IPSO、 SMM得到的总执行时间基本相同， 趋于最优.

从图3(b)中可以看出， NCIGBA得到的能量均衡率值最大， IPSO和GREED次之， SMM最小， 由前面的分析结果可以看出GREED的总执行时间和总消耗能量远远大于NCIGBA、 IPSO和SMM. 因此， 结合总执行时间、 总消耗能量和能量均衡率3个性能指标， GREED最差， IPSO优于SMM， NCIGBA最优.

为了进一步验证本文方法的有效性， 对SMM、 IPSO、 NCIGBA进行更大规模的实验仿真， 任务数和节点数(n，m)的值分别取(50， 10)、 (50， 25)、 (50， 50)、 (50， 75)和(50， 100)， 分别对应任务数和节点数值之间关系的5种类型， 每种类型随机生成100组不同的数据进行实验， 然后得出各算法的总执行时间平均值(AT)、 总消耗能量平均值(AE)和能量均衡率平均值(ALP)， 实验结果如表2所示.

表2　SMM、 IPSO和NCIGBA实验结果Tab.2　The experimental results of SMM、 IPSO and NCIGBA

从表2可以看出， 随着节点数的增加， SMM、 IPSO和NCIGBA得到的平均总执行时间、 平均总消耗能量和平均能量均衡率值呈减少趋势， 并且下降的幅度慢慢减少. 对于任务数和节点数之间值大小的五种不同类型， IPSO总体优于SMM， 而NCIGBA的各项性能指标均优于IPSO和SMM.

6　结语

针对无线传感器网络任务调度过程中造成的资源冲突问题， 本文将其视为节点间的非完全信息博弈竞标过程， 并提出一种非完全博弈竞标算法进行资源分配， 此算法以一种自主的观点进行资源分配， 具有自适应特性， 同时也能很好满足于网络的动态性和异构性. 最后在实验仿真部分证明了NCIGBA得到的总执行时间、 总消耗能量和能量均衡率三个优化性能指标均优于GREED、 SMM和IPSO.

[1] ZIMMERMAN A T, LYNCH J P, FERRESE F T. Market-based resource allocation for distributed data processing in wireless sensor networks[J]. ACM Transactions on Embedded Computing Systems,2013, 12(3): 84:1-28.DOI:10.1145/2442116.2442134.

[2] SCHRAGE D, FARNHAM C, GONSALVES P G. A market-based optimization approach to sensor and resource management[C]//Intelligent Computing: Theory and Applications IV.Priddy:SPIE, 2006.DOI:10.1117/12.665153.

[3] LEE D H, HAN J H, KIM J H. Market-based multiagent framework for balanced task allocation[M]//Robot Intelligence Technology and Applications 2012. Berlin:Springer, 2013: 549-559.DOI:10.1007/978-3-642-37374-9_53.

[4] EDALAT N, XIAO W, THAM C K,etal. A price-based adaptive task allocation for wireless sensor network[C]// 2009 IEEE 6th International Conference on Mobile Adhoc and Sensor Systems. Macau: IEEE, 2009: 888-893. DOI:10.1109/MOBHOC.2009.5337039.

[5] KHAN M I, RINNER B, REGAZZONI C S. Resource coordination in wireless sensor networks by combinatorial auction based method[C]// 2012 IEEE 3rd International Conference on Networked Embedded Systems for Every Application. Liverpool:IEEE, 2012: 1-6. DOI:10.1109/NESEA.2012.6474012.

[6] VISWANATH A, MULLEN T, HALL D,etal. MASM: a market architecture for sensor management in distributed sensor networks[C]// Multisensor, Multisource Information Fusion: Architectures, Algorithms, and Applications 2005. Florida: SPIE, 2005: 281-289.DOI:10.1117/12.604074.

[7] BANGLA A K, CASTANON D. Asynchronous auction for distributed nonlinear resource allocation[C]// 2011 50th IEEE Conference on Decision and Control and European Control Conference. Orlando: IEEE, 2011: 4 467-4 472.DOI:10.1109/CDC.2011.6161247.

[8] LI Y, GAO Z, YANG Y,etal. An improved auction scheme for task allocation in wireless sensor network[C]// 2010 6th International Conference on Wireless Communications Networking and Mobile Computing. Chengdu: IEEE, 2010: 1-4.DOI:10.1109/WICOM.2010.5601143.

[9] 翁楚良, 陆鑫达. 一种基于双向拍卖机制的计算网格资源分配方法[J]. 计算机学报, 2006, 29(6): 1 004-1 009.

[10] 李立, 刘元安, 马晓雷. 基于组合双向拍卖的网格资源分配[J]. 电子学报, 2009, 37(1): 165-169.

[11] 陶军, 吴清亮, 吴强. 基于非合作竞价博弈的网络资源分配算法的应用研究[J]. 电子学报, 2006, 34(2): 241-246.

[12] 李志洁, 程春田, 黄飞雪, 等. 一种基于序贯博弈的网格资源分配策略[J]. 软件学报, 2006, 17(11): 2 373-2 383.

[13] 李明楚, 许雷, 孙伟峰, 等. 基于非完全信息博弈的网格资源分配模型[J]. 软件学报, 2012, 23(2): 428-438.

[14] XIA T, GUO W, CHEN G. An improved particle swarm optimization for data streams scheduling on heterogeneous cluster[M]//Advances in Computation and Intelligence. Berlin: Springer, 2007: 393-400.DOI:10.1007/978-3-540-74581-5_43.

[15] WU M Y, SHU W, ZHANG H. Segmented min-min: a static mapping algorithm for meta-tasks on heterogeneous computing systems[C]//Heterogeneous Computing Workshop. Cancun: IEEE, 2000.DOI:http://doi.ieeecomputersociety.org/10.1109/HCW.2000.843759.

(责任编辑： 蒋培玉)

A non-complete information game bidding method for resource allocation in wireless sensor networks

ZHANG Shunhua1, LIU Zhanghui1, 2

(1. College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China;2. Fujian Provincial Key Laboratory of Network Computing and Intelligent Information Processing, Fuzhou, Fujian 350116, China)

For the resource conflicts issue caused during task scheduling in wireless sensor networks, we consider it as the non-complete information game bidding process between the nodes. When the joined nodes make decisions, we introduce the hidden Markov chains to predict the decisions of other competitors. Meanwhile, we assign the optimization objectives of resource allocation problem to the task agents and node agents, and propose a non-complete information game bidding algorithm. Finally, under the assumption of joined node individual rationality, we demonstrate that this non-complete information game bidding model meet the principles of incentive compatibility and maximize system revenue. And its validity be proved from simulation experiments.

wireless sensor networks; resource allocation; bidding; game

10.7631/issn.1000-2243.2016.01.0045

1000-2243(2016)01-0045-07

2014-03-11

刘漳辉(1971-)， 副教授， 主要从事智能网络技术研究， lzh@fzu.edu.cn

国家自然科学基金项目(61103175); 教育部科学技术研究重点项目(212086); 福建省科技创新平台项目(2009J1007); 福建省高校杰出青年人才计划项目(JA12016); 福建省高校新世纪人才计划项目(JA13021)

TP393

A