一种由横波激发的特殊非线性声现象

张世功，吴先梅，张碧星，周红生



一种由横波激发的特殊非线性声现象

张世功1, 2，吴先梅2，张碧星2，周红生1

(1. 中国科学院声学研究所东海研究站，上海200032；2. 中国科学院声学研究所，北京100190)

目前对非线性超声的研究多集中在纵波激发的谐波性质以及对材料微观结构变化的实验检测上，横波激发的非线性声波性质少有研究。对横波激发的一维非线性声波方程入手，利用摄动法求解该方程，并改写为一阶偏微分方程，然后利用交错网格的有限差分形式进行数值求解。结果表明：采用横波激发，能产生线性横波和非线性纵波，且纵波的高次谐波内有两个信号，分别以纵波和横波两种速度传播。若采用较长的激发信号，纵波谐波能形成“拍”现象，成为一种奇特的声传播现象。

非线性声波；纵谐波；横波激发；摄动法

0 引言

有限振幅纵波激发的非线性声波具有以下特征[1-3]：在传播过程中畸变，变化为锯齿波或三角波等；在传播过程中，信号能量由基频波向谐波传递；波形畸变的程度由非线性声波的幅度决定，当然频率、非线性系数等一些物理参量也对畸变有较大影响；激波或冲击波产生；除了谐波产生之外，非线性声波还有一个性质就是能够对两个不同频率的输入信号进行调制，形成差频波(或称混频波、调制波等)等；纯纵波可以单独传播，但纯横波不能脱离纵波单独传播[2]；最后一个特点说明用横波激发时，不但会产生横波，还会产生纵波。

Landau和Murnaghan比较早地研究了固体介质中的非线性声学问题[4-5]，得到了各向同性介质内非线性声波方程，人们利用这一方程对介质的非线性进行了大量的研究，范围主要集中在固体介质微观变化的检测评估上，而这些应用都偏重于利用纵波进行检测，横波检测相对较少。但随着科技的发展，利用横波激发产生的纵谐波对材料进行评价也逐渐开展起来[6]。

在固体介质里，横波激发产生纵波是一个普通的正常现象，而如果是无限大固体材料，又是平面横波激发，还能产生纵波则有些不符合理论[7]，为此，本文对有限振幅横波激发产生的非线性声波进行了理论研究。

首先，将非线性声波简化，得到一维非线性声波方程，利用数值计算对该方程进行仿真，对得到的非线性声波信号进行分析，得到了一些由横波激发的非线性声波的性质：横波激发的非线性声波产生幅度略微下降的线性横波，但不产生横波的谐波信号。同时还产生了纵波的谐波，且纵谐波里包含两种速度的声信号，一种以纵波的速度传播，另一种以横波的速度传播，成为一种比较特殊的非线性声现象。

1 理论基础

考虑一维模型的二维振动问题，即声传播方向为方向，质点振动方向为、方向，对Goldberg推导的非线性声波进行简化[1-3]，得到一维的非线性声波方程：

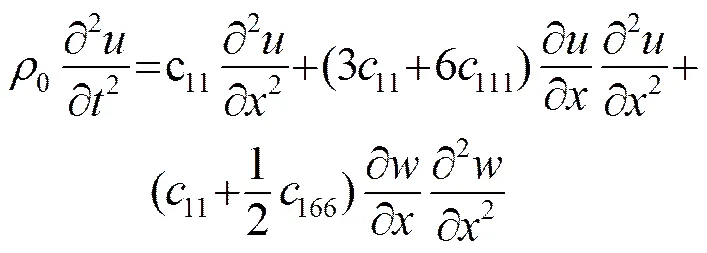
(1b)

式中：、为、方向的振动位移；11、44、111、166分别是二阶弹性系数和三阶弹性系数，为固体材料相应的线性和非线性弹性参数。

方程(1)可以采用摄动方法进行求解[3]，令，设其解为：

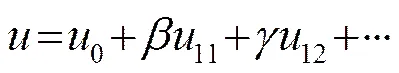
(2b)

将其代入方程(1)，可得：

(3b)

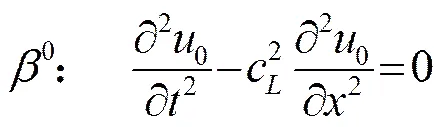
(4b)

对于横波激发的波传播问题，线性声波方程(4a)、(4b)相互不耦合，采用横波激发的方式不能获得纵波的线性信号，即，而线性横波方程的解为：；由于，方程(5a)、(5b)、(6b)中右侧的源信号为0，均不能产生有效的声信号。但对于方程(6a)，方程右侧的源信号中包含0，方程可写作：

(7)

该方程为非齐次方程，因为波动方程描述了方程的振动(纵波)，而非齐次项却含有横波的波数，这个非齐次方程的解需要利用波方程Duhamel原理来解[8-9]，得到的解为

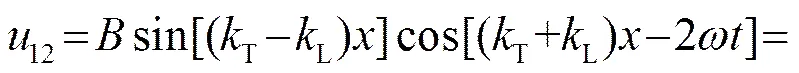
(8)

式中：为与纵波波速、横波速、声源以及介质参数有关的常数：

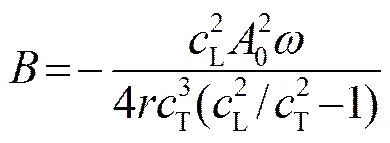
从方程的解式(8)中可以看出，横波激发的纵波解中有两个二次谐波，分别以纵波速度和横波速度传播，这是一个相对奇特的声学现象，由于摄动法并不能得到信号的瞬态解，为此对方程(1)开展了数值解的研究。

2 数值仿真

将方程(1)转换为一阶差分形式，然后利用有限差分方法对非线性方程进行计算，考虑到,，可写作：

(10b)

其中，设应变为

(10d)

方程(10)可以利用有限差分方法进行计算，其振动速度和应变的交错网格格式差分方程为：

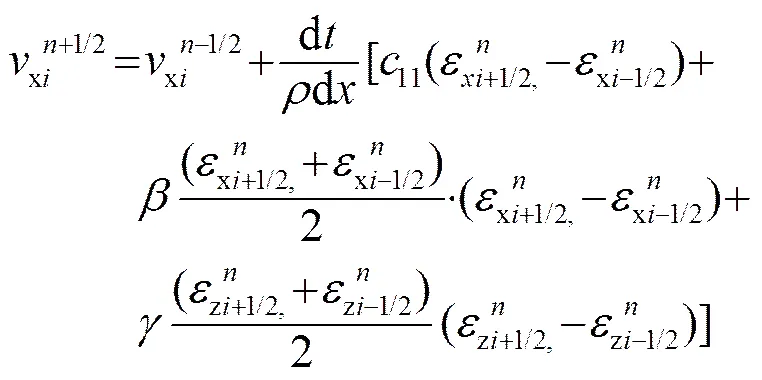
(11b)

(11c)

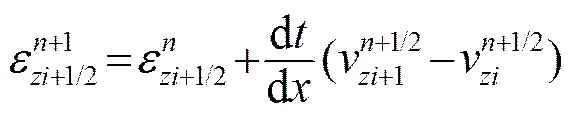
建立一维固体模型，材料为铝，其相应参数[10]见表1，相关文献[11]对材料非线性系数的正负进行过讨论，不同材料的非线性系数有正有负，在数值计算中非线性系数的正负也只是影响波形畸变的位置是出现在位移大于零还是小于零的部分，而实验信号中波形畸变出现的位置也不尽相同[12]。

表1 铝介质的声学参数

数值计算采用横波来激发，声源位于模型左侧节点上，取方向质点振动速度为声源信号，其幅度为19 m/s，形状为5个周期的正弦波加窗调制，频率为500 kHz。由于一维模型的计算量相对较少，将模型的长度设得较长(0.5 m)，只研究声波还没有到达右边界的情况，即可不必考虑右边界反射问题。空间和时间步长分别为52.4 μm和6.94 ns。

3 结果及讨论

计算得到某时刻的x方向传播的质点振动速度和方向的质点振动速度声场如图1所示。

计算结果中可以明显发现方向的振动速度幅度与声源相当，为线性信号或基频信号。而与传播方向平行的方向振动的纵波信号则幅度较小，与方向振动的线性信号比较，可以明显发现其为二次谐波信号。结果表明，即使是一维模型，横波声源激发也可以产生纵谐波，其幅度比线性信号小得多。但是较为奇特的是纵谐波信号中有两个信号，一个以纵波速传播，一个以横波速传播。沿方向传播并在方向振动的纵波信号竟然能以横波速度传播，这并不太符合传统声学中的理论。暂且称在方向振动并与横波速度相同的二次谐波为横波速纵波。对于非线性声学理论，虽然横波不能单独存在，它的传播必须要有纵波伴随，但在方向振动又在方向传播，却具有横波的传播速度，这有点难以理解。

一些文献[13-14]称采用横波激发时不会产生二次横谐波，但对数值计算中产生的横波信号进行频谱分析后却发现含有奇数次谐波，如图2所示。

数值计算时，方程(10)并未将谐波分阶次计算，所以计算的纵波(方向振动)和横波(方向振动)信号是所有的阶次都在一起的。横波激发既然产生了纵波谐波信号，方向就有相应的应变，又产生振动速度，而根据耦合情况就会产生横波的谐波。值得注意的是，由于方向的速度和应变都是较小的谐波信号，所以再次耦合出来的横波信号幅度较小，阶次更高，最小为三阶谐波，计算结果中仅有奇次谐波，原因还有待分析。

数值计算的纵波信号还有一个奇特的现象，由于计算的方向的振动速度中，以纵波速度传播的信号振动速度一直为正，而以横波速度传播的信号振动速度一直为负，这样会形成位移信号是一个包，这也与物理常识有出入。

上面解的形式和利用摄动法的解有所差异，摄动解中只是说明纵波解中有二次谐波和两种速度，两种速度的波耦合在一起形成“拍”现象。但数值计算的现象中未出现该现象，分析原因为：摄动解是一个稳定的解，而数值求解却是瞬态解，为此，采用连续波输入，将输入信号拉长，取中间较为稳定的解，方向振动信号见图3。可以看出，质点振动速度信号振幅被调制，同时具有纵波和横波成分，与摄动解形式完全一致。

邓明晰教授[14]在其专著中讨论了纵波和横波形成的“拍”现象，横波可以自作用产生二次谐波纵波并伴随横波，由于两种波相速度不同，存在一个异步的相互作用，并产生“拍”现象。这和上述讨论的问题有一定的吻合之处。

横波激发的非线性纵波有一定的复杂性，它比弦的大振幅横振动[15]更加复杂，并且不容易解释，同时，这种应用相对较少，所以本文不再加以讨论。

4 结论

横波激发的非线性声波，能产生线性横波和纵波谐波，且纵谐波以纵波和横波两种速度传播，并能形成“拍”现象。为非线性声波传播的基础研究提供了初步的理论指导。

[1] Green R E. Treatise on materials science and technology: ultrasonic investigation of mechanical properties[M]. NewYork: Academic Press, 1973: 73-126.

[2] Goldberg Z A. Interaction of plane longitudinal and transverse elastic waves[J]. Sov. Phys. Acoust, 1960, 6(3): 306-311.

[3] 钱祖文. 非线性声学[M]. 北京: 科学出版社, 2009, 332-400.

QIAN Zuwen. Nonlinear acoustics[M]. Beijing: Science Press, 2009: 332-400.

[4] 朗道, 栗弗席兹. 弹性理论[M]. 武际可, 刘寄星译. 北京: 高等教育出版社, 2011: 120-123. Landau L B, Lifshitz E M. Theory of elasticity[M]. WU Jike, LIU Jixing translate. Beijing: High Education Press. 2011: 120-123.

[5] Murnaghan F D. Finite deformation of an elastic solid[M]. New York: Chapman & Hall Limited. 43-95.

[6] Jiang W H., Li L L. Du G H. Nonlinear propagation characteristics of transverse waves in anisotropic solids[C]//Ultrasonics Symposium, 1995. Proceedings., 1995 IEEE (Volume:1).

[7] 张海澜. 理论声学[M]. 北京: 高等教育出版社, 2007: 434-439. Zhang Hailan. Theoretical acoustics[M]. Beijing: High Education Press, 2007: 434-439.

[8] 布利克, 科达斯. 基础偏微分方程[M]. 李俊杰译. 北京: 高等教育出版社, 2006: 309-324. Bleecker D, Csordas G. Basic partial differential equations[M]. LI Junjietranslate. Beijing: High Education Press. 2006: 309-324.

[9] 易卜拉欣莫夫. 非线性数学物理问题[M]. 卢琦译. 北京: 高等教育出版社, 2010: 162. Ibragimov, I. A. Nonlinear mathematical physics problem[M]. LU Qi translate. Beijing: High Education Press. 2010. 162.

[10] Thomas J. Third-order elastic constants of aluminum[J]. Physical Review, 1968, 175(3): 955-962.

[11] Stratoudaki T, Ellwood R,.Sharples S, et al. Measurement of material nonlinearity using surface acoustic wave parametric interaction and laser ultrasonics[J]. J. Acoust. Soc. Am., 2011, 129(4): 1721-1728.

[12] Breazeale M A, Philip J. Determination of third-order elastic constants from ultrasonic harmonic generation measurements in Physical acoustics[M]. Edited by W. P. Mason. Orlando: Academic Press. 1984: 1-60.

[13] NORRIS A N. Symmetry conditions for third order elastic moduli and implications in nonlinear wave theory[J]. J. Elasticity, 1991, 25(3): 247-257.

[14] 邓明晰. 固体板中的非线性兰姆波[M]. 北京: 科学出版社, 2006: 1-22. DENG Mingxi. Nonlinear lamb wave in solid plate[M]. Beijing: Science Press, 2006: 1-22.

[15] 莫尔斯. P M, 英格特 K U. 理论声学[M](下册). 杨训仁等译. 北京: 科学出版社, 1986: 991. Morse P M, Ingard K U. Theoretical acoustics[M]. YANG Xunren translate. Beijing: Science Press, 1986: 991.

A special nonlinear phenomenon excited bytransverse wave source

ZHANG Shi-gong1, 2, WU Xian-mei2, ZHANG Bi-xing2, ZHOU Hong-sheng1

(1.Shanghai Laboratory, Institute of Acoustics,Chinese Academy of Sciences, Shanghai 200032, China; 2.Institute of Acoustics,Chinese Academy of Sciences, Beijing100190,China)

Studies of nonlinear acoustics mostly concentrate on the problems relevant to the longitudinal harmonic waves generated by longitudinal waves at present. Nonlinear waves generated by transverse wave are seldom studied. In this paper, the nonlinear acoustic wave equation for the two dimensional oscillation propagating in one dimension direction is studied and solved by perturbation method. First the nonlinear acoustic wave equation is reformed intofirst order partial differential equation, and then the finite difference method in staggered grid style is performed to obtain the numerical solution. The results show that the linear transverse wave and nonlinear longitudinal wave can be observed with a transverse source; two signals in the longitudinal harmonic waves can propagate with longitudinal and transverse wave velocities respectively; and the clap phenomena of longitudinal harmonic waves can be seen in the nonlinear wave, which becomes a special acoustic propagation phenomenon. The results can provide a theoretical guidance for the basic study of nonlinear acoustic wave propagation.

nonlinear acoustics; longitudinal harmonic wave; excited by transverse wave; perturbation method

O422.7

A

1000-3630(2016)-03-0218-04

10.16300/j.cnki.1000-3630.2016.03.006

2016-01-10;

2016-03-10

国家自然科学基金资助项目(11274337)

张世功(1979－), 男, 河南鄢陵人, 博士, 研究方向为非线性声学, 超声检测, 激光超声。

张世功, Email: wuxm@mail.ioa.ac.cn