基于卡尔曼滤波的航姿参考系统设计*

吴　涛，白　茹，朱礼尧，钱正洪

（杭州电子科技大学磁电子中心，杭州310018）

基于卡尔曼滤波的航姿参考系统设计*

吴涛，白茹，朱礼尧，钱正洪*

（杭州电子科技大学磁电子中心，杭州310018）

针对传统的航姿参考系统AHRS（Attitude and Heading Reference System）中姿态角精度不高的问题，设计了一种新型的基于卡尔曼滤波的姿态检测系统。该系统采用了三轴磁传感器、三轴陀螺仪及三轴加速度计，用四元数的方法来描述载体运动的姿态，通过陀螺仪测姿态四元数，卡尔曼滤波算法融合加速度计和磁传感器数据，对姿态四元数进行修正，从而提高姿态解算精度。实验数据表明，系统能够较好修正陀螺仪漂移，且三个角度的均方根误差均优于0.25°，具有良好的噪声抑制能力。

传感器；航姿参考系统；卡尔曼滤波；四元数；陀螺仪；加速度计；磁传感器

EEACC:7230；7310Fdoi:10.3969/j.issn.1004-1699.2016.04.012

姿态检测系统是一种能够精确测量载体在三维空间中姿态角的惯性测量系统。在三维空间中一般用俯仰角、横滚角、航向角表示其姿态角信息。在军事、航空航天、航海等领域一般采用高精度的机械陀螺仪或激光陀螺仪［1］，但是价格昂贵；随着消费电子产品的智能化程度不断提高，姿态检测系统越来越多地应用于消费类的无人机、智能家电等领域，价格低廉的MEMS传感器得到了广泛应用［2，3］。然而，MEMS陀螺仪存在严重的零点漂移和随机误差，原始角速率在经过积分后解算的姿态角精度较低，难以独立应用。三轴加速度计可以测量重力场矢量在载体坐标系下的加速度值，由坐标系转换矩阵可以求出载体的俯仰角和偏航角；三轴磁传感器可以测量地磁场数据在载体坐标系下的磁场值，同样由坐标转换矩阵可以求出载体的航向角［4］。当这几个传感器分别独立工作时，都会由于各自的局限性而导致较大偏差。卡尔曼滤波可以利用陀螺仪来预测姿态角，用加速度计和磁传感器的数据来进行修正，将几个传感器优势互补，从而解算出高精度的姿态数据。

1　姿态四元数原理

设由运载体的机体轴确定的坐标系为b，惯导系统所采用的导航坐标系为n，则由b系到n系的坐标变换矩阵表示为，利用惯性器件的输出实时计算出便可进行姿态更新。由于n系和b系均为直角坐标系，且各轴之间始终保持垂直，因此，两坐标系的空间位置关系即可理解为刚体的定点转动。

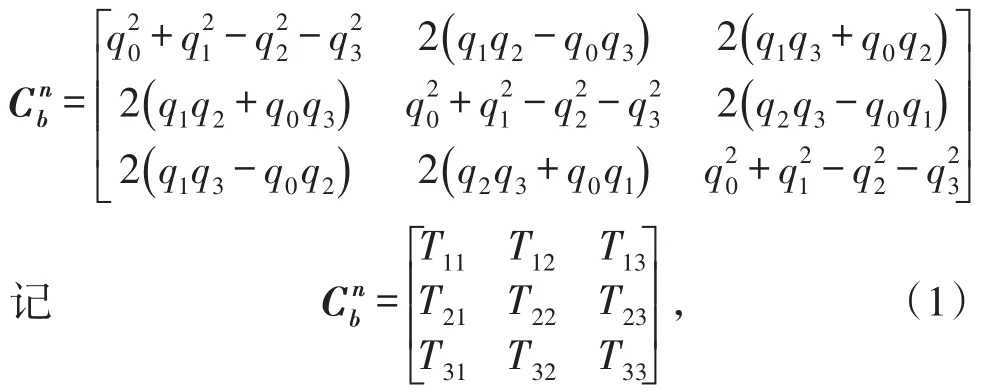
求解坐标变换矩阵的关键在于更新姿态四元数，四元数微分方程如下［5］:

以东北天坐标系为地理坐标系，ψ、θ、γ分别为运载体的航向角、俯仰角、横滚角，则用欧拉角表示的b系至n系的坐标变换矩阵为:

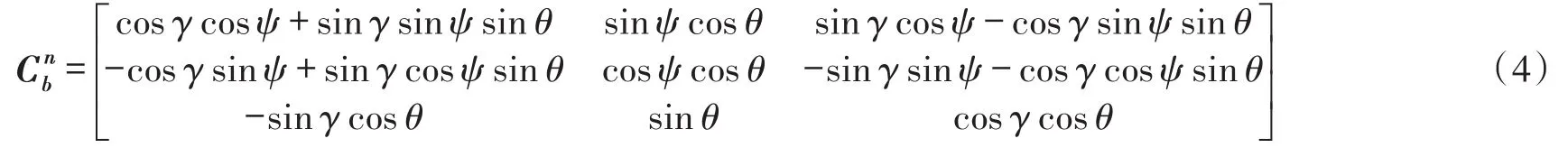
对比式（1）和式（4）即可得出姿态角如下:

2　卡尔曼滤波在姿态解算中的应用

在消费类的电子产品的设计中，MEMS传感器由于低廉的价格使其迅速占领了市场，但是其漂移的缺点也降低了传感器数据输出的精度。实际应用中需要设计合适的算法对误差数据估算，并将多个传感器数据进行融合，以提高数据的解算精度。对传感器数据进行融合的方法有多种，常用的有最速下降算法和卡尔曼滤波算法等。最速下降算法是利用负梯度方向来决定每次迭代的新的搜索方向，使每次迭代后待优化的目标函数逐步减小［6-7］。本文采用的卡尔曼滤波算法是一套由计算机实现的实时递推算法，所处理的对象是随机信号，利用系统噪声和观测噪声的统计特性，以系统的观测量作为滤波器的输入，以所要求的估计值（系统的状态变量）作为滤波器的输出，滤波器的输入和输出由时间更新和观测更新算法联系在一起，根据系统的状态方程和观测方程估算出所需要处理的信号［8］。

2.1姿态检测系统设计

姿态检测系统以加速度计、陀螺仪及磁传感器的输出数据进行校准后作为系统输入，经过卡尔曼滤波进行数据融合，并解算出姿态角输出。常用六位置校准法校准三轴加速度计［9］，建立硬磁和软磁模型并采用合适的补偿算法可以对磁传感器进行标定［10］。本文所采用的卡尔曼滤波算法中，将四元数以及陀螺仪漂移误差组成的七维向量作为状态向量。采用四元数的方法，与欧拉角的方法相比避免了大量的三角函数运算，提高了更新速率，保证了实时性，还不会出现奇异值；另外将陀螺仪的误差引入状态向量中可以实时预测陀螺仪的漂移误差，并及时校正。将磁传感器的输出和加速度计的输出分别校准后作为观测向量。卡尔曼滤波姿态解算系统框图如图1所示。

图1　卡尔曼滤波姿态解算框图

2.2状态方程

系统的状态方程表示为:

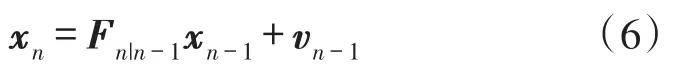
其中，xn表示系统n时刻的状态向量［11］，且为n-1时刻系统状态噪声，且

在陀螺仪数据输出率较高的情况下，在较短的时间间隔Δt内，可近似认为角速率不变，根据式（2）中的四元数微分方程，可以对角速率积分，以此对四元数进行更新，姿态四元数的更新方程为:

根据式（6）和式（7）可得，系统状态转移矩阵:

2.3观测方程

系统的观测方程表示为:

其中，zn表示系统 n时刻的观测向量，且为n时刻系统观测噪声，且

取东北天坐标系为地理坐标系，则地理坐标系下重力场矢量和地磁场矢量分别表示为:

其中mnx、mny、mnz分别为东北天坐标系下地磁场测量值，可通过GPS得到当地磁倾角以及磁偏角，由地磁场矢量求得。

以地理坐标系为导航坐标系，则将导航坐标系下的重力场矢量转换到载体坐标系，则可得出载体坐标系下的重力场矢量为［12］:

将导航坐标系下的地磁场矢量转换至载体坐标系，则有:

记

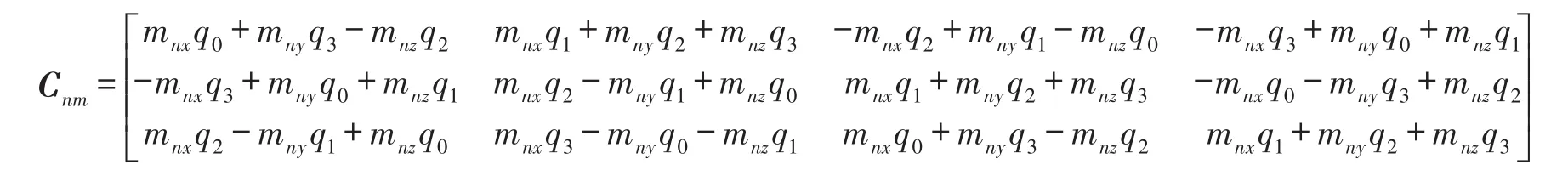
则

由式（11）和式（12）可得观测矩阵为:

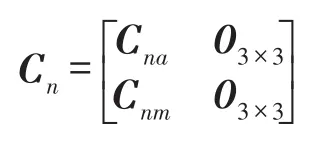
2.4卡尔曼滤波算法流程

由状态方程和观测方程均为离散方程，所以用离散卡尔曼滤波进行递推滤波计算［11］。在每一个滤波周期中，包括状态预测、状态估计流程和增益矩阵、误差自相关矩阵计算流程，其具体步骤如下［13］:

状态向量中对四元数的初始化应满足归一化，一般取［0001］T，误差自相关矩阵P0为非零的矩阵，可取nI，其中，n≠0，I为单位矩阵。

步骤3一步预测误差自相关矩阵。

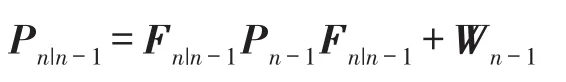
步骤4新息过程自相关矩阵。

步骤5卡尔曼增益计算。

步骤6状态估计。

步骤7状态估计误差自相关矩阵。

说明:在计算过程中由于积分误差、单片机精确度问题导致四元数出现误差，因此在每次更新之后都需要对四元数进行归一化，以保证下次更新之前数据的可靠性。

3　实验结果

3.1姿态检测模块静态测试

采用以上方法解算姿态角，对姿态检测模块进行静态测试，采集数据并分析。在测试过程中，将姿态检测模块固定，分析姿态数据。本次实验主要分析静态条件下姿态角的随机误差和漂移情况。将姿态检测模块固定之后采集15 000组（150 s）姿态数据，其结果如图2所示。

图2　卡尔曼滤波姿态角静态误差

由图2可看出在较长时间运行后，姿态曲线依然保持“水平”，而且没有出现漂移的趋势，证明此算法具有良好的漂移抑制能力。

将以上数据分析，计算其均方根误差如表1所示。

表1　姿态角静态均方根误差

3.2姿态检测收敛性测试

将姿态检测模块分别用最速下降算法和卡尔曼滤波算法解算，并进行收敛性测试对比。首先用最速下降算法进行姿态解算，将模块静止放置稳定后，将其旋转一个较小的角度，并采集姿态角输出如图3所示。用同样的方法对卡尔曼滤波算法进行收敛性测试，其姿态角输出如图4所示。

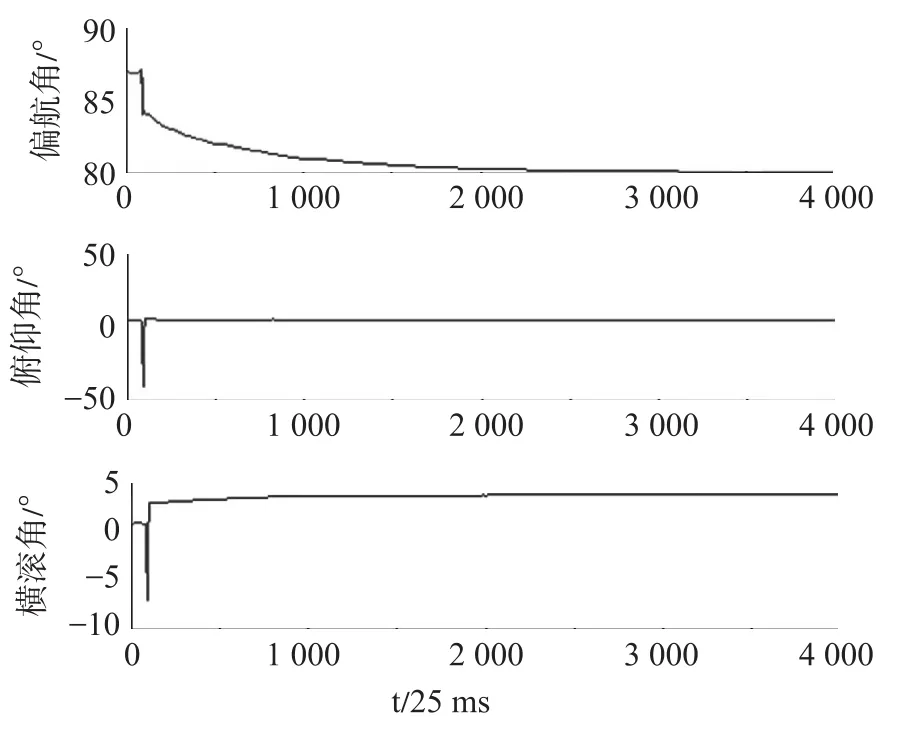
图3　梯度下降算法收敛性测试

图4　卡尔曼滤波算法收敛性测试

由图3、图4可知，最速下降算法中航向角收敛最慢，在37.5 s（1500）之后，数据收敛情况良好；而用卡尔曼滤波算法3个姿态角都在1.5 s（150）之内已经收敛，且数据稳定。由此得出结论，此卡尔曼滤波算法与最速下降算法相比，极大地提高了收敛速度，具有较好的动态响应。

4　结束语

本文基于卡尔曼滤波姿态解算方法对传统姿态测试系统进行了改进，获得了较传统的电子罗盘更高的动态性能，并且有效地修正了陀螺仪的漂移误差，提高了姿态解算精度。该系统可以用于与姿态控制有关的工业控制领域及消费电子产品的应用中。

［1］ 李荣冰，刘建业，曾庆化，等.基于MEMS技术的微型惯性导航系统的发展现状［J］.中国惯性技术学报，2004（6）:90-96.

［2］ 蔡春龙，刘翼，刘一薇.MEMS仪表惯性组合导航系统发展现状与趋势［J］.中国惯性技术学报，2009（5）:562-567.

［3］ 杨业飞，申文涛.惯性稳定平台中陀螺技术的发展现状和应用研究［J］.飞航导弹，2011（2）:72-79.

［4］ 杨续伟.基于微惯性组合的嵌入式航姿参考系统研究［Z］.上海交通大学，2012:硕士，79.

［5］ Kamnik R，Stegel S，Munih M.Design and Calibration of Three-Axial Inertial Motion Sensor:Power Electronics and Motion Control Conference，2006.EPE-PEMC 2006.12th International［Z］. 2006:2031-2036.

［6］ 孙金秋，游有鹏，傅忠云.基于共轭梯度法和互补滤波相结合的姿态解算算法［J］.传感技术学报，2014，27（4）:524-528.

［7］ 余星.基于捷联惯性的水下载体姿态检测系统研制［Z］.杭州电子科技大学，2013:硕士，92.

［8］ 杨淑洁，曾庆双，伊国兴.低成本无人机姿态测量系统研究［J］.传感器与微系统，2012，25（2）:15-18.

［9］ 宋丽君，秦永元.MEMS加速度计的六位置测试法［J］.测控技术，2009（7）:11-13.

［10］赵鑫炉，张晓明，白渚铨，等.基于磁阻传感器的航姿测量系统罗差补偿技术研究［J］.传感技术学报，2013，26（11）:1504-1507.

［11］盛汉霖，张天宏，刘冬冬.基于扩展卡尔曼滤波器的低成本航姿系统设计［J］.系统工程与电子技术，2013（10）:2158-2164.

［12］伊程毅.基于地磁和微惯性器件组合的姿态测量系统研究［Z］.哈尔滨工业大学，2013:硕士，77.

［13］Madrigal Sastre H，Durand S，Marchand N.Design and Implementation of an Attitude and Heading Reference System（AHRS），2011.CCE 2011.8th International Conference on［Z］.2011，1-5.

吴涛（1989-），男，杭州电子科技大学电子信息学院硕士研究生，主要研究方向为传感器应用和惯性导航；

钱正洪（1967-），男，杭州电子科技大学电子信息学院教授、博士生导师，从事磁电子材料和集成功能器件的研究，zqian@hdu.edu.cn。

Design of AHRS Based on Kalman Filter*

WU Tao，BAI Ru，ZHU Liyao，QIAN Zhenghong*
（Center for Integrated Spintronic Devices，Hangzhou Dianzi University，Hangzhou 310018，China）

A new attitude detecting system based on Kalman filter is designed for the problem of low precision of attitude angle in the tradition Attitude and Heading Reference System（AHRS）.Three-axis magnetic sensor，three-axis accelerometer and three-axis gyroscope are integrated in the system.An attitude estimation method based on quaternion is adopted to describe the attitude of carrier.Attitude quaternion is calculated by the gyroscope，and the data of accelerometer and magnetic are fused by Kalman filter to fix quaternion and improve the accuracy of attitude.The experimental data shown that the system could compensate the drift error of gyroscope better，the root mean square error of both three angles wrer better than 0.25°，and the ability of noise reduction was better than the tradition AHRS.

sensor；ahrs；kalman filter；quaternion；gyroscope；accelerometer；magnetic

TP212 6

A

1004-1699（2016）04-0531-05

项目来源:浙江省科学技术厅重大科技专项重点工业项目（2011C11047）；浙江省科学技术厅公益项目（2013C31073）

2015-10-28修改日期:2016-01-05