一种旋转角加速度传感器标定方法的研究*

赵　浩，冯　浩

（1.嘉兴学院南湖学院，浙江嘉兴314001；2.杭州电子科技大学自动化学院，杭州310018）

一种旋转角加速度传感器标定方法的研究*

赵浩1*，冯浩2

（1.嘉兴学院南湖学院，浙江嘉兴314001；2.杭州电子科技大学自动化学院，杭州310018）

针对旋转角加速度传感器标定困难这一问题，提出了一种能够校准旋转角加速度传感器的方法。角加速度激励源采用伺服电动机产生，被校准的传感器与激励源同轴连接，通过调节激励源的电参数，能够产生幅值可调的旋转角加速度量值，测取角加速度传感器的输出电压值后即可实现标定。本文详细阐述了激励源的角加速度产生机理，推导了角加速度量值的理论公式，给出了计算角加速度量值所需参数的测取方法，最后对感应式角加速度传感器进行了校准实验，验证了标定方法的可行性。

角加速度；旋转磁场；椭圆度；有效匝数比

EEACC:7230；7320Edoi:10.3969/j.issn.1004-1699.2016.04.006

旋转角加速度是一个非常重要的动态角参量，通过对角加速度的测量，就可以分析旋转系统转轴对各种激励的响应情况［1］。目前，旋转角加速度测量在汽车、军事、航空航天、工业、电子等多个领域得到了广泛的应用［2-5］。

由于旋转角加速度的测量精度很大程度上依赖于标定的准确度，因此旋转角加速度的校准技术也开始受到重视，国内外很多学者在这一方面进行了大量的研究。例如，薛景峰采用精密角度编码器和衍射光栅激光干涉仪，研制出频率范围为0.25 Hz～550 Hz、角加速度范围为0.1 rad/s2～1 760 rad/s2的角振动绝对法校准装置［6］；魏敏根据质量—转动惯量等效原理，提出了一种多维角加速度传感器的静态标定方法［7］；刘晓敏设计了一种基于伺服电机和单片机系统的角加速度标定装置［8］；高扬根据线加速度和角加速度的关系，对角加速度值进行了测定［9］；杨雪松采用正弦激励法对回转角加速度进行了测量［10］；德国联邦物理技术研究院在国际上率先建立了角振动国家标准装置［11］，美国、日本、韩国等许多国家的计量机构正在开展动态角运动校准技术研究［12］；此外还有通过对角位移或者角度进行微分处理后来校准角加速度的间接标定方法，但测量误差较大，不适于作为动态角运动量计量标准的溯源途径［12］。

本文提出了一种能够校准旋转角加速度传感器的方法，阐述了角加速度激励源的工作机理，推导了角加速度量值的理论公式，最后采用该方法对感应式角加速度传感器进行了标定实验，得到了传感器的性能指标。该方法能够对角加速度量值进行直接溯源，且激励源产生的角加速度量值具有较高的信噪比，能够保证标定结果具有较高的准确度。

1　角加速度激励源工作原理

角加速度激励源一般分为电磁式和电机式，本文采用的角加速度激励源为单相感应电动机，其定子绕组为主、副两相绕组，在空间上互相正交，且副绕组一般为串接电容后与主绕组并联。当主、副绕组通入交流电后，两相绕组分别产生脉振磁场，对两个脉振磁场在直轴和交轴这两个正交的方向进行分解，合成后分别为Φ1（t）和Φ2（t），一个周期的波形如图1所示，其数学表达式为:

图1　一个周期的脉振磁场波形图

根据磁场合成法则，幅值不同的两个脉振磁场，合成后为如图2所示的椭圆旋转磁场，其中φ（t）为t时刻旋转磁场转过的角位移。

图2　椭圆旋转磁场示意图

由图1和图2可知，当ωt从0增至90°时，磁场Φ1（t）幅值由0增至Φ1m，磁场Φ2（t）幅值一直为0；当ωt从90°增加时，开始形成旋转磁场，转向为顺时针方向，当 ωt从 90°到 180°变化时，0＜φ（t）＜90，且有:

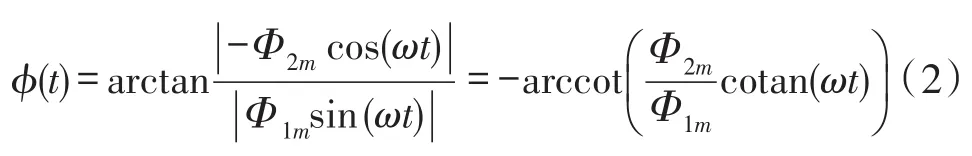
对一个周期内其余时间段磁场转过的角度φ（t）做类似推导，得到的结果均为式（2）所示。然后对式（2）进行二阶求导，即可得到任意t时刻椭圆旋转磁场的角加速度为:

式中αe=Φ1m/Φ2m≤1，定义为旋转磁场的椭圆度。

单相感应电动机理想空载运行时，转子电流为零，转子与旋转磁场同步转动，即转子的角加速度与椭圆旋转磁场的角加速度相同。假设交流电压的频率为50 Hz，则根据式（1）和式（3）可知，旋转磁场的角加速度变化频率为绕组通电频率的2倍，即为100 Hz，采用数值计算软件对αe=0.8时旋转磁场的角加速度进行仿真，结果如图3所示。

图3　旋转磁场角加速度波形图

由此可知，如果能够测取旋转磁场的椭圆度信息αe，就可以根据式（3）得到相应的转子旋转角加速度量值。

2　椭圆度αe的测量

椭圆度的获取需要得到直轴和交轴两个正交方向脉振磁场的幅值。忽略主、副绕组的漏阻抗，根据变压器公式，主绕组电压与产生的磁通量和副绕组电压与产生的磁通量，满足方程:

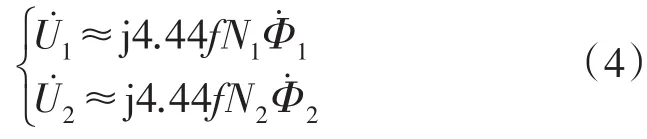
式中f为通电频率，N1和N2分别为主、副绕组的有效匝数。由于电动机工作时为副绕组串接电容后与主绕组并联，由此可知:

图4　电压-磁通关系相量图

将图中副绕组产生的磁通量进行分解，分量一与主绕组产生的磁通量方向一致，分量二与主绕组产生的磁通量方向垂直，由此可得:

式中K=N1/N2，为主、副绕组的有效匝数比。

3　主副绕组有效匝数比的测定

为了获取旋转磁场的椭圆度信息，需要测取主、副绕组的有效匝数比，测定方法如图5所示。首先对主绕组施加额定电压U1N，如图5（a）所示，产生的磁通量为Φ1，忽略主绕组的漏阻抗，则存在:

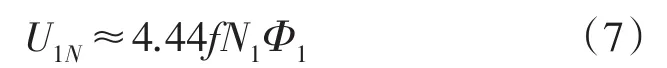
设转子的结构参数为常数Ce，电动机空载运行，转速为n1，则转子导条切割磁通量Φ1产生的动生电动势为:

电动势的方向可以根据右手定则判断，如图5（a）所示。设转子导条的等效电阻为R，则转子导条电流为:

假设电机磁路不饱和，磁化系数为K，则转子导条电流产生的磁通量为:

副绕组开路，则副绕组中的感应电动势为:

联立式（7）～式（11），可得:

图5　测定主、副绕组有效匝数比原理图

然后对副绕组施加电压U2，如图5（b）所示，产生的磁通量为Φ2，忽略副绕组的漏阻抗，则存在:

电机同样空载运行，设此时转子转速为n2，则转子导条切割磁通量Φ2产生的动生电动势为:

感应电动势的方向用右手定则判断，如图5（b）所示。此时转子导条中的电流为:

假设电机磁路不饱和，则转子导条电流产生的磁通量为:

主绕组开路，则主绕组中的感应电动势为:

联立式（13）～式（17），可得:

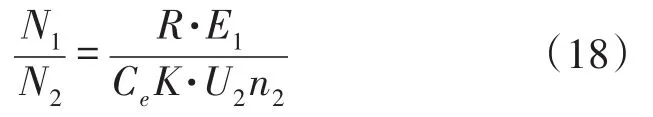
式（12）与式（18）相乘可得:

根据式（19）可以得到主、副绕组的有效匝数比。

4　角加速度传感器标定实验与分析

实验装置采用浙江大学求是科技的NMCL-II型电机及传动试验台，角加速度激励源的转轴通过刚性联轴器与角加速度传感器［1］同轴连接，此外还包括传感器电源和数字存储示波器，如图6所示。

图6　角加速度传感器标定实验装置

4.1主、副绕组有效匝数比的测定

根据文中阐述的主副绕组有效匝数比测定方法，首先主绕组施加电压U1N=220 V，副绕组开路，电动机空载，测得副绕组的感应电动势为E2=243.6 V，转速n1=1 481 r/min；然后主绕组开路，副绕组施加电压U2=310 V，电动机空载运行，测得主绕组的感应电动势E1=118.1 V，转速n2=1 477 r/min。将数据代入式（19）可得主副绕组的有效匝数比为K=N1/N2=0.587 4。

4.2传感器标定实验与分析

角加速度激励源施加电压后开始运行，角加速度传感器输出的电压波形如图7所示，波形的大致趋势与图3一致。由此可知激励源产生的角加速度量值，以及传感器输出信号都具有较高的信噪比，能够保证标定结果的准确度。

图7　角加速度传感器输出电压波形

改变激励源的电压信号，记录主、副绕组和电容两端的电压，根据式（6）得到旋转磁场的椭圆度信息，再根据式（3）得到角加速度量值。为了便于分析，实验时采用峰-峰值对应的方法进行标定，即角加速度峰值-传感器输出电压峰值对应。实验数据如表1所示，对应的标定曲线如图8所示，对表1的实验数据进行线性拟合，由此得到的角加速度传感器灵敏度约为10.1 mV/（krad/s2），线性误差约为1.7%。

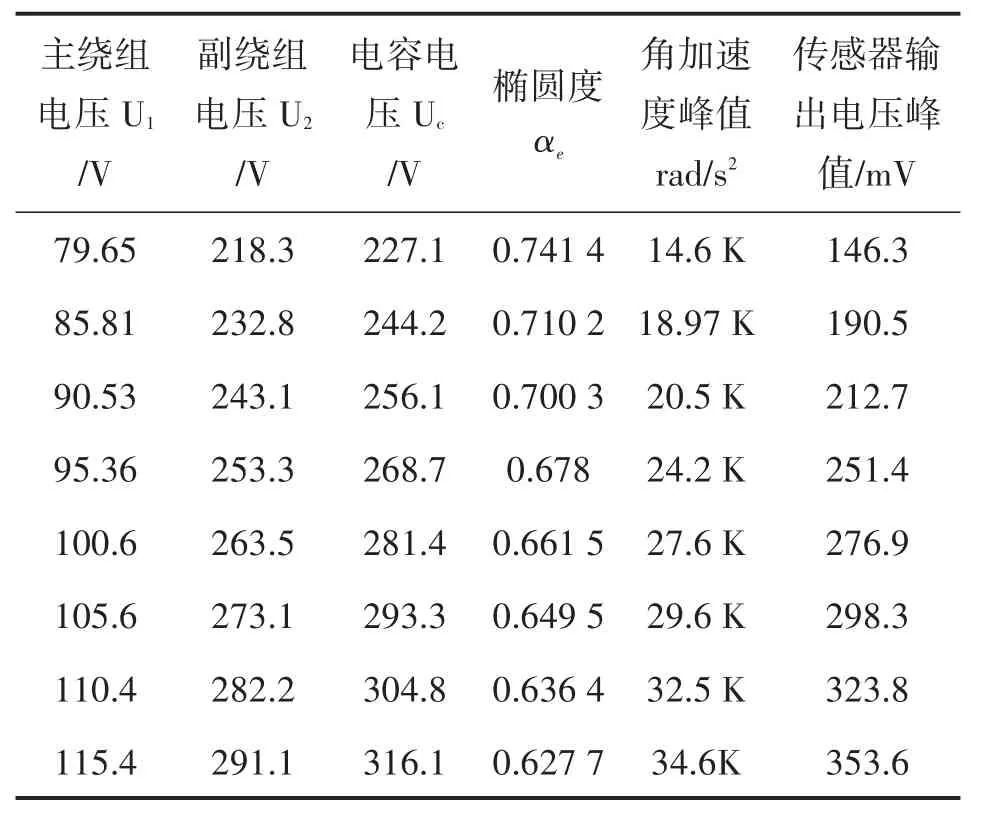
表1　传感器标定实验结果

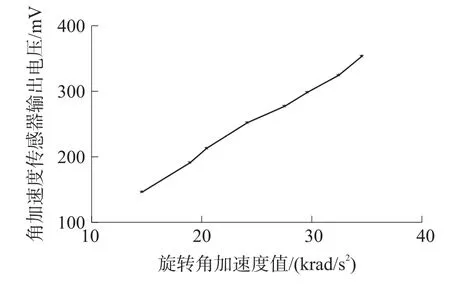
图8　角加速度传感器标定曲线

造成线性误差的原因主要源自角加速度量值的计算过程:椭圆度计算和主、副有效匝数比测量过程中，忽略了主、副绕组的漏阻抗；角加速度激励源实际空载运行时转子导条存在感应电流，产生的磁场与旋转磁场耦合作用；主、副绕组以及电容电压测量时产生的测量误差；采用式（3）进行角加速度量值计算时的小数位数取舍误差。

5　结论

本文提出了一种角加速度传感器的标定方法，详细阐述了激励源产生角加速度量值的工作原理，以及如何获取计算角加速度量值所需要的参数，最后对实际的角加速度传感器进行了标定，验证了该方法的可行性和有效性。该方法能够实现角加速度量值的直接溯源，相对比较法具有较高的准确度，可望得到推广和应用。

［1］ 赵浩，冯浩.基于电磁感应原理的永磁角加速度传感器研究［J］.传感技术学报，2012，25（9）:1257-1261.

［2］ Tran V H，Lee S G.A Stable Formation Control Using Approximation of Translational and Angular Accelerations Int［J］.Adv Robot Syst，201:1，65-75.

［3］ 于翔，李醒飞，徐梦洁.一种磁流体陀螺的设计研究［J］.传感技术学报，2013，26（11）:1483-1487.

［4］ Weenk D，van Beijnum B J F，Baten C T M，et al.Automatic Identification of Inertial Sensor Placement on Human Body Segments during Walking.［J］.Neuroeng.Rehabil，2013，10，doi:10.1186/ 1743-0003-10-31.

［5］ Rueterbories J，Spaich E G，Andersen O K.Characterization of Gait Pattern by 3D Angular Accelerations in Hemiparetic and Healthy Gait［J］.Gait Posture，2013（2）:183-189.

［6］ 薛景峰，彭军，李新良.角振动校准装置研究［J］.宇航学报，2015，36（3）:1-8.

［7］ 魏敏，吴忠城，戈瑜.多维角加速度传感器静态标定方法研究［J］.仪器仪表学报，2005，26（3）:286-289.

［8］ 刘晓敏，赵云伟.一种精确的小型运动传感器标定方法与应用［J］.长春大学学报，2015，25（10）:6-8.

［9］ 高扬，张新磊，麦吉.基于加速度计的旋转平台角加速度检测方法［J］.宇航计测技术，2015，35（2）:14-16.

［10］杨雪松，李长春，母东杰.正弦激励法在传感器校准中的新应用［J］.传感器与微系统2014，33（7）:154-156，160.

［11］Taubner A，Martens H.Measurement of Angular Accelerations，Angular Velocities and Rotational Angles by Grating Interferometry ［J］.Measurement，1998（24）:21-32.

［12］彭军，何群，孙丰甲.动态角运动校准技术综述［J］.计测技术，2008，28（5）:1-4，9.

赵浩（1983-），男，讲师，主要研究方向为新结构传感器的设计、旋转机械与传动系统振动特性分析及抑制方法研究。主持浙江省自然科学基金、浙江省教育厅科研项目和嘉兴市科技计划项目等多项课题，在Sensors、J VIBROENG和传感技术学报、计量学报等期刊上发表多篇论文，zhaohao204@163.com；

冯浩（1956-），男，教授，一直从事电机与检测、人工神经网络技术与应用方面的研究和开发工作。主持国家自然科学基金、浙江省重大科技专项、留学回国人员基金、浙江省自然科学基金等课题多项；已发表论文60余篇，其中有多篇论文被SCI、EI收录，zjhzfh@126.com。

Research of a Calibration Method for Rotating Angular Acceleration Sensor*

ZHAO Hao1*，FENG Hao2
（1.Nanhu College of Jiaxing University，Jiaxing Zhejiang 314001，China；2.Automation college of Hangzhou Dianzi University，Hangzhou 310018；China）

For the calibration problem of angular acceleration sensor，a calibration method is presented in this paper. The angular acceleration excitation source is generated by servo motor，and angular acceleration sensor is connected with the excitation source coaxially.The amplitude of angular acceleration can be adjusted by adjusting electrical parameters of excitation source，the characteristic of sensor is received after measuring the sensor output voltage.In this paper，the working mechanism of angular acceleration excitation source is described in detail，the theoretical formula of angular acceleration is deduced，and the parameters measuring method for calculating angular acceleration is given.Finally，a induction angular acceleration sensor is calibrated by this method，and the feasibility is verified.

angular acceleration；rotating magnetic field；ellipse；effective turns ratio

TP212

A

1004-1699（2016）04-0495-05

项目来源:国家自然科学基金项目（51541507）；浙江省自然科学基金项目（LQ14E050007）；嘉兴市科技计划项目（2015AY11018）

2015-10-29修改日期:2015-12-25