基于频域超分辨的高速目标参数估计算法

王 钊 王鹏毅 苏卫民 王 玮 杜冰馨



基于频域超分辨的高速目标参数估计算法

王 钊*①②王鹏毅①苏卫民②王 玮①杜冰馨①

①(中国电子科技集团公司第五十四研究所 石家庄 050081)②(南京理工大学电子工程与光电技术学院 南京 210094)

针对宽带噪声雷达高速目标探测中参数估计性能与运算复杂度无法兼顾的问题，该文提出一种基于频域超分辨的参数估计算法。该算法通过设置不同固定时延得到多组含有不同相位信息的组合噪声调频信号，并对每组信号进行不含尺度变换的匹配滤波运算，以此来构造多普勒相位差组。根据多普勒相位差组与阵列信号处理的相似性，利用现代谱估计算法得到目标的速度信息，构造多普勒补偿函数进行包含尺度变换的匹配滤波运算估计出目标的距离信息。该算法可以在无需考虑多普勒色散的情况下估计出目标速度，整个运算过程仅需1次时域重构运算；当多普勒相位差组的固定时延及分组数选择合适时，其运算复杂度及参数估计性能皆优于曲面拟合的宽带互模糊函数算法。仿真结果验证了该算法的有效性。

宽带噪声雷达；多普勒色散；多普勒相位差组；频域超分辨

1 引言

宽带噪声雷达具有低截获概率、良好的抗干扰和反电子对抗等性能，在现代化高技术战争中具有广阔的应用前景。然而宽带噪声雷达在探测运动目标时受到两方面影响，一方面来自于载波的多普勒频移，另一方面来自于包络的伸缩变换，也就是多普勒色散，这些均会导致常规匹配滤波算法的性能下降[5,6]。

针对这两方面问题很多学者提出了相应的解决方法，宽带互模糊函数(Wideband Cross Ambiguity Function, WCAF)算法凭借其近似最大似然的估计性能而受到更多的关注[7,8]。但是WCAF算法应用于噪声雷达时需要进行运算复杂度较大的时域重构运算，以及距离-速度的2维搜索过程，不利于工程实现[9]。为了弥补这一缺陷，文献[10]提出了一种组合噪声调频信号，在此基础上采用最小二乘(Least Squares, LS)算法对目标的距离及速度信息进行联合估计。这种算法虽然运算复杂度较低，但是却存在两方面缺陷：(1)当雷达场景中存在多个目标时，该算法需要先将相同目标的轨迹关联出来，然后再针对单个目标进行参数估计；(2)该算法虽然运算量很低，但是当多普勒色散积较大时，其参数估计性能较差。

MUSIC(MUltiple Signal Classification, MUSIC)是一种在阵列信号处理中估计非相关信源的超分辨空间谱估计算法。近年来，MUSIC算法在宽带雷达参数估计领域的应用屡见不鲜[11,12]。文献[11]将MUSIC算法运用到噪声雷达相干处理系统，来抑制多普勒色散现象所导致的频谱失真现象，但是这种算法仅适用于多普勒色散积较小的情况。文献[12]采用类宽带DOA算法在慢时间维估计多普勒频率，然后构造多普勒补偿函数并估计出目标时延，但是该算法仅能解决脉间距离走动的问题，而没有考虑脉内的多普勒色散现象。

结合MUSIC算法，本文提出了一种基于频域超分辨(Frequency Domain Supper-Resolution, FDSR)的高速目标参数估计算法。首先给出了组合噪声调频(Component Noise Frequency Modulation, CNFM)信号的多目标回波模型，然后通过设置不同的固定时延得到多组含有不同相位信息的CNFM信号，并对每组信号进行不含尺度变换的匹配滤波运算，以此来构造多普勒相位差组。接着根据多普勒相位差组与阵列信号处理的相似性，利用MUSIC算法估计出目标的速度信息，并进一步分析了该信号组中信源的相关性以及固定时延及分组数目的选取范围。最后构造多普勒补偿函数进行包含尺度变换的匹配滤波运算，通过高斯拟合估计出目标的时延信息。仿真结果给出了固定时延及分组数目不同时，目标参数估计的性能分析，验证了本文算法的有效性。

2 超分辨估计算法

2.1 多目标回波模型

(2)

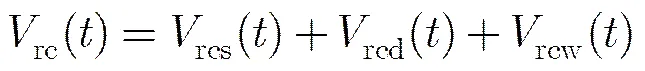
(4)

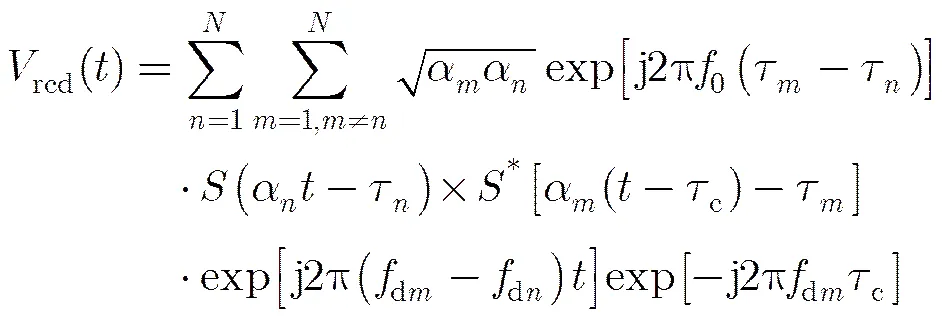
(6)

2.2 目标多普勒估计

分别对每组信号进行匹配滤波以后，可得

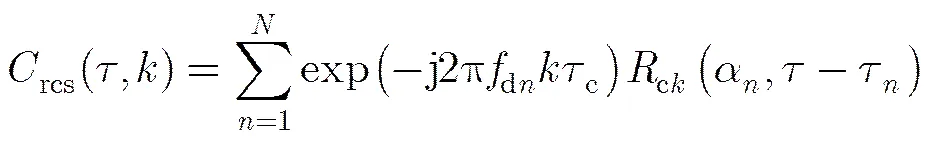
(9)

同时定义每组噪声调频信号的多普勒相位向量：

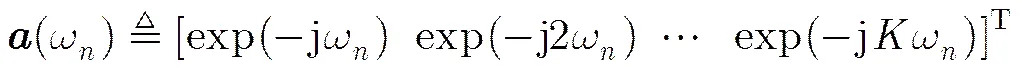
其中，

(12)

从式(11)中可以看出，该多普勒相位差组的结构与窄带阵列信号处理的结构完全一致，因此可以利用阵列信号处理中空间谱估计的方法，通过多普勒相位差组的多普勒向量估计出目标的速度。采用MUSIC谱估计算法[14]，可得

(14)

2.3 目标时延估计

抑制噪声雷达的窄带多普勒敏感特性可以通过构造多普勒补偿函数来实现，根据MUSIC算法估计所得的多普勒频率，多普勒补偿函数可以构造为。将回波信号与相乘可得载频多普勒补偿以后的回波信号，接着还需要抑制宽带多普勒敏感的部分。根据多普勒频率以及尺度因子与目标速度的关系，可以将尺度因子用表示为，接着对回波信号进行尺度因子为的伸缩变换，经过伸缩变换以后可得速度完全补偿的回波信号为。

2.4 估计算法流程

综上所述，估计算法的具体流程如下：

(2)重复(1)中步骤次，每次固定时延增加，构成组CNFM信号；

(3)每组信号分别进行匹配滤波，构成多普勒相位差组；

(4)利用构造的多普勒相位差组进行改进的MUSIC谱估计以求得目标的速度信息；

3 算法性能分析

3.1 信源相关性分析

上一节介绍的MUSIC算法只有在信源间相互独立时有效，当信源相关时MUSIC算法的估计性能会变差。当信源完全相关时，信源协方差矩阵会出现秩亏损，使得信号特征向量发散进噪声子空间，从而导致某些信源的信号子空间与噪声子空间不完全正交，影响谱估计性能。在空间谱估计中导致信源相关的原因主要是多径效应，本文算法涉及的信源相关类型与空间谱估计略有不同，具体分析如下：

从式(13)中可以看出本文涉及的信源为CNFM信号的宽带相关函数,仅在附近存在峰值，而在其他地方均为随机噪声。假设两目标信源分别为及，根据文献[15]中给出的宽带多普勒敏感特性，与仅存在时延位置以及主瓣宽度上的不同，当两目标的宽带相关函数发生重叠时，便会出现信源相关的情况。根据与的重叠程度，信源相关性存在以下几种情况：

可见，当两目标的参数相近时，也会出现信源相关的情况，导致MUSIC算法在估计多普勒频率时出现损失。改进的MUSIC算法是较常用的解决相关信源谱估计的算法[16]，该算法通过添加一个非相关的阵列向量来解决秩亏损的问题，具体算法本文不再赘述。

3.2 运算复杂度分析

本文提出的基于FDSR的高速目标参数估计算法的运算复杂度(复乘)分析如下。假设回波信号长度为，多普勒相位差组分组数为，观测的距离门数为，那么在构造多普勒相位差组时所需运算量为，计算正反协方差矩阵的运算量为，特征分解的运算量为，目标数为，采用求根MUSIC算法时构造求根多项式并求根的运算量为，多普勒补偿及时延估计时的运算量为，进而获得FDSR算法总的运算量为。由于在实际应用中，的取值通常为数万，而为30以下()，那么与的运算量也将远远小于，可以忽略分组数对时间复杂度的影响，那么FDSR算法的时间复杂度可以计为。根据文献[7]可得基于LS的估计算法总的运算量为,为短时相关分段数，取值通常为20左右，那么LS算法的时间复杂度可以表示为。二次曲面拟合-宽带互模糊函数(QSF-WCAF)算法总的运算量为,为互模糊函数速度搜索次数，为了获得较高的粗估计精度，的取值通常为数百以上，那么QSF-WCAF算法的时间复杂度为。对比3种算法的时间复杂度可以得出，LS算法的时间复杂度最低，FDSR算法次之，最高为QSF-WCAF算法。

3.3 信噪比损失

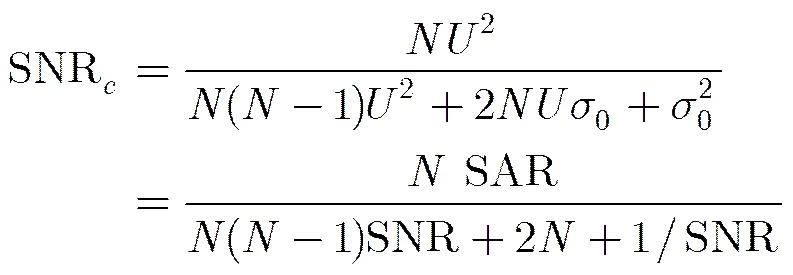
3.4 分组数目选取

在阵列信号处理中，阵元数越多，空间谱估计的性能也就越好。但是对于本文算法，情况并非如此。由于本文算法都是建立在假设成立的基础上，而CNFM产生时采用的固定时延为，随着信号组的增加，最大固定时延也会增加。当增大到一定程度时，的假设将不成立。下面将给出成立时分组数的取值范围分析。

(17)

3.5 固定时延选取

4 仿真及结果分析

下面将通过计算机仿真来验证本文所提理论及算法的有效性。假设雷达发射宽带噪声调频连续波信号，参数设置为：信号载频，带宽，时宽，采样频率, Monte Carlo实验次数同为100次。

图2给出了两目标信源相关程度不同时，采用MUSIC算法以及改进MUSIC算法进行谱估计的性能对比图。其中，多普勒相位差分组数，固定时延间隔, SNR为。当信源高度相关时，两目标参数分别设置为,,，图2(a)和图2(b)分别给出了MUSIC算法及改进MUSIC算法的频谱图。可以看出，此时MUSIC算法基本失效，而改进MUSIC算法仍然可以估计出信源的多普勒频率。图2(c)和图2(d)分别给出了MUSIC算法及改进MUSIC算法的特征值，可以看出MUSIC算法仅能估计出一个目标，而改进的MUSIC算法仍然可以估计出目标的真实数目；当信源完全独立时，两目标参数分别设置为,,,，图2(e)和图2(f)分别给出了MUSIC算法及改进MUSIC算法的频谱图。可以看出，改进MUSIC算法得到的谱峰高度要高于MUSIC算法。综上所述，在信源相关性较强时，MUSIC算法性能变差甚至失效，而改进MUSIC算法可以有效地改善相关信号的谱估计结果；在信源为非相关信号时，改进MUSIC算法也优于MUSIC算法的性能。

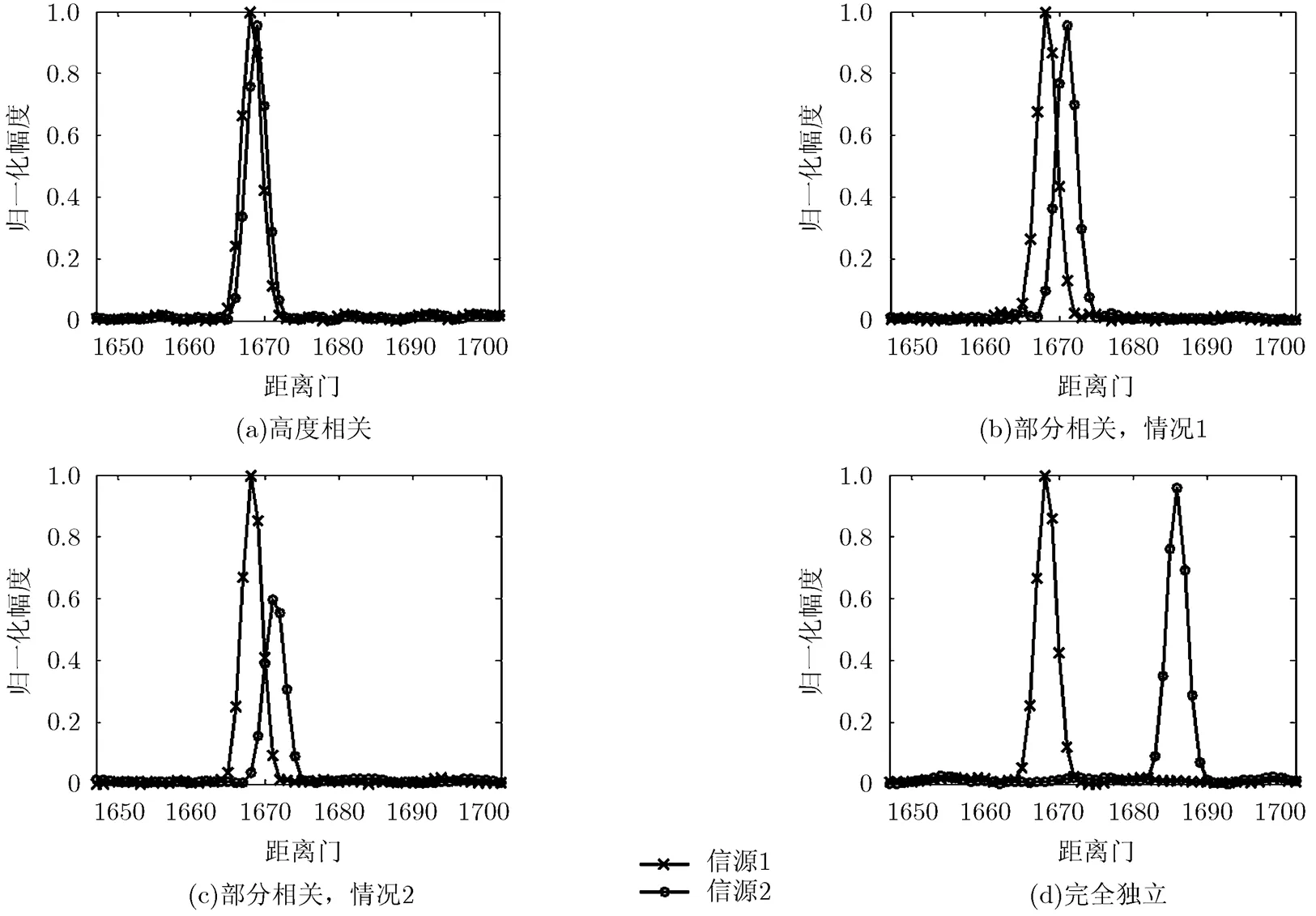
图1 信源相关性示意图

图2 MUSIC算法与改进的MUSIC算法谱估计结果对比图

图3(a)和图3(b)给出了固定时延间隔而改变多普勒相位差组分组数时，FDSR算法在相同SNR情况下与WCAF算法的均方根误差曲线对比图。其中SNR为0 dB，固定时延间隔相同为，多普勒相位差组分组数,由5增加至35且步进间隔为3, WCAF算法采用QSF-WCAF算法。可以看出，目标的速度估计误差会随着分组数的增加而减少，而距离估计误差变化较小，其原因是由于目标速度估计误差较多普勒敏感速度过小而对距离估计影响较小所致。同时，在分组数目变化的过程中，距离估计误差一直低于QSF-WCAF算法，而速度估计误差在分组数大于5时低于QSF-WCAF算法。图3(c)和图3(d)给出了固定多普勒相位差组分组数而改变固定时延间隔时，FDSR算法在相同SNR情况下与WCAF算法估计均方根误差曲线对比图。其中SNR为0 dB，这里与图3(a)和图3(b)设置相同的多普勒相位差组孔径，将统一为由增加至且步进间隔为，对应的固定时延间隔由增加至且步进间隔为，多普勒相位差组分组数固定为20。从图3(c)和图3(d)可以看出，目标的速度估计误差会随着固定时延间隔的增加而减少，与图3(a)和图3(b)的分析类似，此时距离估计误差基本没有变化。同时，在固定时延间隔变化的过程中，距离估计误差一直低于QSF-WCAF算法，而速度估计误差在固定时延间隔大于时低于QSF-WCAF算法。图3(e)和图3(f)进一步给出了相同孔径时，两种参数分别变化时FDSR算法的目标参数估计误差对比。可以看出，改变固定时延间隔对估计误差的影响要小于改变多普勒相位差组分组数，且相同孔径时，多普勒相位差组分组数越大估计误差越小。

图4给出了FDSR算法、LS算法及QSF-WCAF算法的均方根误差曲线。其中输入SNR从变化至且步进量为, FDSR算法的固定时延间隔为，多普勒相位差组分组数为20, LS算法的分段数目为16且每段信号的多普勒色散积为0.1, WCAF算法采用QSF细化方法。可以看出在距离及速度估计时，FDSR算法的估计性能都要明显优于QSF-WCAF算法及LS算法。

图5给出了FDSR算法及LS算法与QSF- WCAF算法运算时间比值的对比图。其中观察距离门数为100，样本点数的变化范围为到, QSF-WCAF算法的速度搜索次数为100, FDSR算法的多普勒相位差组分组数为20，为了保证多普勒色散较小，假设LS算法的分段样点数为，则分段数为由100至1000。可以看出，由于FDSR算法与QSF-WCAF算法时间复杂度的阶数相同，其运算效率改善不随样本点数变化，而LS算法的时间复杂度为线性阶，运算效率的改善较高，且随着样本点数的增加而愈加明显。

图3 分组数、固定时延和孔径对估计误差的影响

图4 3种算法的均方根误差曲线图           图5 算法的运算复杂度分析

5 结束语

采用最小二乘结合组合噪声调频信号的参数估计方法，可以有效地解决宽带噪声雷达在探测高速目标时存在的多普勒敏感及多普勒色散问题，但是该算法在探测多目标时面临目标配对的问题，且仅适用于多普勒色散积较小的情况。本文提出了一种基于频域超分辨的高速目标参数估计算法(FDSR)。该算法通过构造多普勒相位差组，在匹配滤波未尺度化的失配情况下，利用改进的MUSIC算法仍然可以预先估计出目标的速度信息，进而构造尺度匹配参考信号来估计目标的时延信息。然后详细分析了多普勒相位差组中的信源相关性情况，推导了固定时延间隔及分组数目的参数选择上限，并得出合理的设置固定时延可以有效抑制多普勒模糊的结论。仿真结果表明，(1)参数估计性能随着固定时延及分组数的增加而增加；(2)与最小二乘算法(LS)，以及基于二次曲面拟合的宽带互模糊函数算法(QSF-WCAF)相比，本文算法的参数估计性能最优，运算复杂度介于最小二乘算法与宽带互模糊函数算法之间。

参考文献

[1] ZHOU X L, WANG H Q, CHENG Y Q,. Statistical angular resolution limit for ultrawideband MIMO noise radar[J]., 2015: 440-443. doi: 10.1155.2015.906313.

[2] HERMAN J N, REINHARD F, and ANDREAS S. A fully-integrated 77-GHz UWB pseudo-random noise radar transceiver with a programmable sequence generator in SiGe technology[J].:, 2014, 61(8): 2444-2455.doi: 10.1109/ TCSI.2014.2309774.

[3] YANG Q L, ZHANG Y H, and GU X. Wide-band chaotic noise signal for velocity estimation and imaging of high-speed moving targets[J]., 2015, 63: 1-15. doi: 10.2528/PIERB15030402.

[4] SHASTRY M, NARAYANAN R M, and RANGASWAMY M. Sparsity-based signal processing for noise radar imaging[J]., 2015, 51(1): 314-325. doi: 10.1109/TAES.2014.130733.

[5] KELLY E J and WISHNER R P. Matched-filter theory for high-velocity, accelerating targets[J]., 1965, 9(1): 56-69. doi: 10.1109/TME. 1965.4323176.

[6] JIN Q, WONG K M, and LUO Z Q. The estimation of time delay and Doppler stretch of wideband signals[J]., 1995, 43(4): 904-916. doi: 10.1109/78.376843.

[7] SINTSYN R B and YANOVSKY F J. Wideband ambiguity function in radar and navigation systems[C]. IEEE 3rd International Conference on Methods and Systems of Navigation and Motion Control (MSNMC) Proceedings, Kiev, Ukraine, 2014: 66-71.

[8] GIUNTA G. Fast estimators of time delay and Doppler stretch based on discrete-time methods[J]., 1998, 46(7): 1785-1797. doi: 10.1109/78.700948.

[9] HO K C and CHAN Y T. Optimum discrete wavelet scaling and its application to delay and Doppler estimation[J]., 1998, 46(9): 2285-2290. doi: 10.1109/78.709507.

[10] 王钊, 顾红, 苏卫民, 等. 基于组合噪声调频信号的高速目标参数估计[J]. 系统工程与电子技术, 2015, 37(9): 1953-1959. doi: 10.3969/j.issn.1001-506X.2015.09.01.

WANG Zhao, GU Hong, SU Weimin,. Parameters estimation of high speed target based on component noise frequency modulation signal[J]., 2015, 37(9): 1953-1959. doi: 10.3969/j.issn.1001- 506X.2015.09.01.

[11] DAWOOD M, QURAISHI N, and ALEJOS A V. Superresolution Doppler estimation using UWB random noise signals and MUSIC[J]., 2013, 49(1): 325-340. doi: 10.1109/TAES.2013.6404106.

[12] YANG L, SU W, GU H,. High resolution velocity estimation and range profile analysis of moving target for pulse LFM UWB radar[J]., 2011, 91(10): 2420-2425. doi: 10.1016/j.sigpro.2011.04.022.

[13] WEISS L G. Wavelets and wideband correlation processing[J]., 1994, 11(1): 13-32. doi: 10.1109/79.252866.

[14] 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2002: 126-135.

ZHANG Xianda. Mordem Signal Processing[M]. Beijing: Tsinghua University Press, 2002: 126-135.

[15] 王钊, 顾红, 苏卫民, 等. 宽带高斯谱噪声雷达高速目标检测[J]. 系统工程与电子技术, 2015, 37(6): 1266-1272. doi: 10.3969/j.issn.1001-506X.2015.06.07.

WANG Zhao, GU Hong, SU Weimin,. Detection of high speed targets in noise radar with wideband Gaussian spectrum[J].,2015, 37(6): 1266-1272. doi: 10.3969/j.issn.1001-506X.2015.06.07.

[16] KUNDU D. Modified MUSIC algorithm for estimating DOA of signals[J]., 1996, 48(1): 85-90. doi: 10.1016/0165-1684(95)00126-3.

王 钊： 男，1985年生，工程师，研究方向为航天测控、噪声雷达的高速目标检测与跟踪.

王鹏毅： 男，1968年生，研究员，研究方向为测控总体技术研究.

苏卫民： 男，1959年生，教授，研究方向为雷达成像理论、随机信号处理.

王 玮： 男，1984年生，工程师，研究方向为航天测控、相控阵雷达信号处理.

杜冰馨： 女，1988年生，助理工程师，研究方向为航天测控、相控阵雷达信号处理.

Parameters Estimation of High Speed Targets Based on Frequency Domain Super-resolution

WANG Zhao①②WANG Pengyi①SU Weimin②WANG Wei①DU Bingxin①

①(54,050081,)②(&,&,210094,)

To solve the contradiction between estimation performance and computation burden, when detecting high speed target in wideband noise radar, a novel method based on Frequency Domain Supper-Resolution (FDSR) is proposed for parameter estimation. Firstly, a group of component noise frequency modulation signals with different phase information are obtained by setting different fixed delay, and the Doppler phase difference group is constructed through matched filtering without scaling transform. Then according to the similarity of Doppler phase difference group and array signal processing, the velocity is acquired through modern spectrum estimation algorithm, and the range is calculated by scaled matched filtering after Doppler compensation. In this method, the velocity is obtained without considering Doppler dispersion and the time-domain reconstruction is used only once in the whole algorithm. The computation burden and estimation performance both superior to wideband cross ambiguity function algorithm based on curve fitting, when the fixed delay and group number of Doppler phase difference group are appropriately selected. The effectiveness of this algorithm is validated by simulation results.

Ksy words: Wideband noise radar; Doppler dispersion; Doppler phase difference group; Frequency Domain Super- Resolution (FDSR)

TN957.51

A

1009-5896(2016)12-3034-08

10.11999/JEIT160058

2016-01-13；改回日期：2016-07-28；

2016-09-30

王钊 alife_numone@126.com

国家863计划项目(2013AA122105)

The National 863 Program of China (2013AA 122105)