基于多项式秘密共享的前摄性门限RSA签名方案
2016-10-13徐甫
徐 甫
基于多项式秘密共享的前摄性门限RSA签名方案
徐 甫*
(解放军信息工程大学 郑州 450002)(北京市信息技术研究所 北京 100094)
现有可证明安全的前摄性门限RSA签名方案均依赖加性秘密共享方法,存在每次签名均需所有成员参与,易暴露合法成员的秘密份额,签名效率低下等问题。该文以Shoup门限签名为基础,提出一种基于多项式秘密共享的前摄性门限RSA签名方案,并对其进行了详细的安全性及实用性分析。结果表明,在静态移动攻击者模型中,该方案是不可伪造的和稳健的,与现有同类方案相比,其通信开销更低,运算效率更高。
门限签名;RSA;多项式秘密共享;前摄性
1 引言
文献[7]最初提出的前摄性门限签名方案是基于离散对数问题的。在为资源受限型网络提供安全服务时,签名方案的运算效率非常重要,而基于离散对数问题的签名方案在该方面并无优势,其签名的验证速度通常比RSA签名方案慢几个数量级[8]。同时,由于RSA签名方案广泛应用于各种场合,研究前摄性门限RSA签名方案具有较大的现实意义和较高的实用价值。自从前摄性门限签名方案的概念提出以来,已出现多种前摄性门限RSA签名方案。其中大部分方案采用加性共享方法实现对私钥的共享,在对给定的消息实施签名时,需要所有个成员共同参与。当某一成员被攻击者捕获而不能产生正确的部分签名时,由其他成员合作恢复其私钥份额并生成合法的部分签名。然而,此类方案存在明显的不足:(1)签名请求者需要与所有个成员通信,增加了网络的通信负担,降低了签名的效率;(2)当某一成员由于通信信道中断等问题而暂时无法响应签名请求时,其他成员会认为其已被攻击者捕获,进而恢复其私钥份额,造成其私钥份额泄露。文献[8]分析指出,对加性共享方法的依赖是目前前摄性门限RSA签名方案存在的主要问题之一。
为了摒弃加性共享方法,使得前摄性门限RSA签名方案能够在移动Ad hoc网络中得到应用,文献[13]引入了多项式共享方法。此外,文献[14]提出的方案虽涉及加性共享方法,但以多项式共享方法为主。然而,文献[13]的方案后来被证明是不安全的[15];文献[14]的方案中,每次签名运算时,所有参与签名的个成员需合作产生一个一次性的加性共享份额,增加了网络的通信负担和节点的运算负担。
本文以采用多项式共享方法的Shoup门限签名方案[16](不具备前摄性)为基础,将其中的加法、乘法和除法运算转移至整数环中,以便于私钥份额更新协议的设计,进而提出一种简单,高效,且可证明安全的前摄性门限RSA签名(Proactive Threshold RSA Signature, PTS-RSA)方案。文章第2节简要介绍了背景及相关工作;第3节详细描述PTS-RSA方案;第4节对提出的方案进行安全性和实用性分析;第5节为结束语。
2 背景及相关工作
参照《中药新药临床研究指导原则》“中药新药治疗慢性肾功能衰竭临床研究指导原则”中的肾虚证及湿热证两种证候的诊断标准[9],拟定肾虚湿热证的标准。主症:腰酸膝软,口中粘腻,肢体困重,纳差,口干,口苦;次症:乏力,脘腹胀满不适,骨痛,恶心,呕吐;舌苔脉象:舌质红苔黄腻或黄厚,脉濡数;诊断条件:主症必备,次症或兼,结合舌脉。
2.1系统模型
(1)一般门限签名方案:一般门限签名方案(不具备前摄性)由密钥生成、签名和验证3个算法组成[2]。
定义1 适应性选择消息攻击:敌手可以在看到签名方案的公钥之后进行任意次的签名查询,而且可以根据已经观察到的签名选择新的消息进行签名查询。
(2)前摄性门限签名方案:前摄性门限签名方案不仅包括密钥生成、签名和验证3个算法,还包括时间段的概念和私钥份额更新协议。前摄性门限签名系统的生存期被划分为多个时间段,在每个时间段的起始阶段,所有成员共同运行私钥份额更新协议,以获得新的私钥份额。前摄性门限签名方案的安全性同样由不可伪造性和稳健性组成。
(3)系统假设:本文假设前摄性门限签名协议在如下通信环境中执行:各成员间时间同步,各成员通过弱同步信道连接,任意两个成员之间具备安全信道,各成员可向所有其他成员发送广播消息。
本文假设前摄性门限签名协议面临静态移动攻击者的攻击:在每个时间段内,攻击者可实施适应性选择消息攻击,最多能够捕获任意不多于个成员,且攻击者在签名协议运行之前预先确定每个时间段内将要捕获的成员。
2.2相关符号及含义
本文基本沿用文献[16]中的符号:
2.3离散对数恒等式协议
文献[16]中提出了一个离散对数恒等式协议。其具体细节如下:
2.4整数环上的拉格朗日插值公式
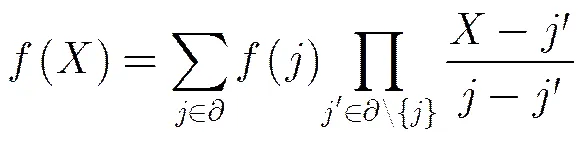
(2)
3 PTS-RSA签名方案
本文提出的PTS-RSA方案包括密钥生成、签名、验证和私钥份额更新4个阶段。
(1)密钥生成:可信中心选择并计算初始参数(各符号含义及相互关系见2.2节)。令,随机选择,,构成多项式。可信中心计算
秘密份额


步骤2 验证并合成部分签名:签名合成者首先验证对每个成员是否成立。如果都成立,则计算。令,由于,可使用扩展欧几里得算法得到满足的和,然后计算,即为信息的标准RSA签名。
(3)验证:验证过程与标准RSA签名方案的验证过程相同,即验证是否成立,如成立则认为群签名有效。
(4)私钥份额更新:在进行私钥份额更新时,采用“零共享”技术[17]:设成员在第时间段内的私钥份额为,则在第次私钥份额更新时,首先,(任一由个成员组成的集合)中的每一成员随机生成常数项为的次多项式,计算,并将通过安全信道发送给成员,如图1所示;然后,每一成员计算,作为其时刻的秘密份额。

图1 “零共享”技术
在实际运行中,私钥份额更新协议还需要验证各种信息的真实性,具体步骤如下:
4 对方案的分析
4.1安全性分析
定理1 (正确性) PTS-RSA方案是正确的。
证明 要证明签名方案的正确性,只要证明签名过程中产生的群签名为标准RSA签名,即即可。
证毕
定理2 (不可伪造性) 如果标准RSA签名方案是适应性选择消息攻击下不可伪造的,那么,面对静态移动攻击者实施适应性选择消息攻击时,PTS-RSA方案是不可伪造的。
证明 为了将PTS-RSA方案的不可伪造性归约至标准RSA签名方案的不可伪造性,我们将构建模拟器SIM,其输入为PTS-RSA方案的所有公开参数。其输出满足:从敌手E(具备适应性选择消息攻击能力的静态移动攻击者)的角度看,与PTS-RSA方案在运行过程中的输出信息是不可区分的。

(4)
(3)在模拟第1次私钥份额更新过程时,SIM首先随机选择集合,并明确与,的关系,假设如图2所示。根据系统模型,对于中的任一成员,攻击者能够掌握其私钥份额增量;对于中的任一成员,攻击者无法掌握其私钥份额增量,否则将导致攻击者在同一时刻掌握大于个成员的私钥份额,与系统模型不符。
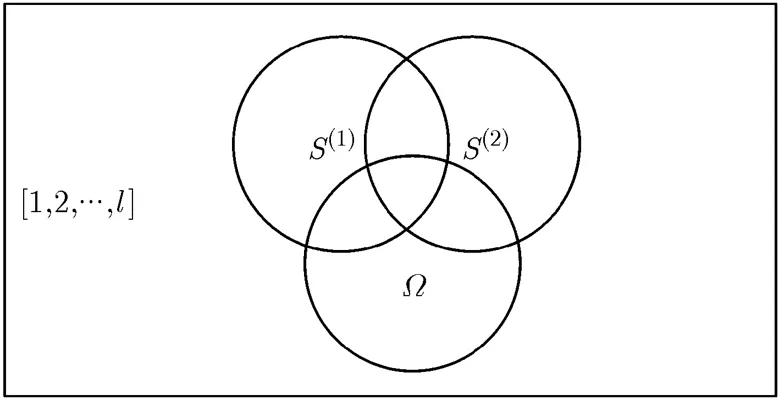
图2 集合关系
现在,假设敌手E能够伪造PTS-RSA方案的群签名,那么,对于PTS-RSA方案所依托的原始RSA签名方案,敌手在不知道其私钥的情况下,可通过向该RSA签名方案进行签名查询获得合法签名对,然后使用SIM模拟出PTS-RSA方案的输出,并调用敌手E攻击PTS-RSA方案的算法来产生新消息的合法群签名,这样,敌手就成功伪造了在原始RSA签名方案中的签名。
证毕
证明 为了证明PTS-RSA方案的稳健性,只需证明当恶意成员发送虚假信息时,能够被合理检测出来即可。这主要包括签名阶段对部分签名,以及私钥份额更新阶段对,和进行正确性验证。其中,对部分签名进行正确性验证的合理性可参阅文献[16]方案中的相关部分。
证毕
4.2 实用性分析
表1列出了现有的前摄性门限RSA签名方案的安全性和使用的秘密共享方法。其中,静态安全表示能够抵抗静态移动攻击者,动态安全表示能够抵抗动态移动攻击者。

表1前摄性门限RSA签名方案的安全性和使用的秘密共享方法
正如引言部分所述,基于加性共享方法的前摄性门限RSA签名方案存在诸多问题。文献[13]方案虽然使用多项式共享方法,但已经被证明是不安全的。文献[14]方案在签名时需要所有签名参与者合作生成一个临时的加性共享份额,增加了通信次数,延长了节点入网认证时间。由表1可知,PTS-RSA方案是目前唯一不依赖加性共享方法、可证明安全的前摄性门限RSA签名方案,由于其签名方法简单,仅需要签名请求者向个成员分别申请部分签名即可,而个成员之间无需任何信息交互,因而非常适合资源受限型网络。下面我们通过PTS-RSA方案与文献[14]方案在通信量和计算量方面的比较来说明PTS-RSA方案在该方面的优势。由于门限签名的密钥生成过程不会频繁进行,该过程所需的运算量及通信量对方案的实用性影响不大,因此,我们主要针对签名阶段和私钥份额更新阶段对两种方案进行对比。同时由于签名和私钥份额更新协议运行的频率也不相同,我们将对这二者进行分别对比。

表2两种方案通信次数
与模指数运算相比,模乘法、模加法和模逆运算的计算量几乎可以忽略,因此,我们通过比较签名方案所需进行的模指数运算次数来比较两种方案的签名效率。表3列出了文献[14]方案、PTS-RSA方案各阶段所需进行的模指数运算次数。当,,时(为文献[14]方案中的安全参数),文献[14]方案在签名和私钥份额更新阶段的所需的模指数运算次数分别为2365和2375,而PTS-RSA方案中相应的数值分别为82和1520。因此,PTS-RSA方案的运算效率高于文献[14]方案,签名效率的优势尤其明显。

表3两种方案模指数运算次数
5 结束语
本文针对现有可证明安全的前摄性门限RSA签名方案均依赖加性共享方法,不能满足资源受限型网络的应用需求这一问题,以文献[16]提出的门限RSA签名方案为基础,将其中的加法、乘法和除法运算均转移至整数环中,结合“零共享”技术,设计了合理的私钥份额更新协议,进而形成一种在通信开销和计算效率方面均优于现有方案的前摄性门限RSA签名方案。在静态移动攻击者模型中对方案的安全性进行了详细的证明。后续工作将集中于研究如何抵抗动态移动攻击者(此类攻击者可根据已掌握的私钥份额和签名来选择新的捕获对象,具有更强的攻击能力),进一步提高签名系统的安全性。
[1] 徐甫, 马静谨. 基于中国剩余定理的门限RSA签名方案的改进[J]. 电子与信息学报, 2015, 37(10): 2495-2500. doi: 10. 11999/JEIT150067.
XU Fu and MA Jingjin. Improvement of threshold RSA signature scheme based on Chinese remainder theorem[J].&, 2015, 37(10): 2495-2500. doi: 10.11999/JEIT150067.
[2] 王洁, 蔡永泉, 田有亮. 基于博弈论的门限签名体制分析与构造[J]. 通信学报, 2015, 36(5): 1-8.doi:10.11959/j.issn.1000- 436x.2015189.
WANG Jie, CAI Yongquan, and TIAN Youliang. Analysis and construction for threshold signature scheme based on game theory[J]., 2015, 36(5): 1-8. doi: 10.11959/j.issn.1000-436x.2015189
[3] 曹阳. 基于秘密共享的数字签名方案[J]. 重庆邮电大学学报(自然科学版), 2015, 27(3): 418-421. doi: 10.3979 /j.issn. 1673-825X.2015.03.021.
CAO Yang. Digital signature scheme based on secret sharing[J].(), 2015, 27(3): 418-421. doi: 10.3979/j.issn.1673-825X.2015.03.021.
[4] KAYA K and SELÇUK A A. Sharing DSS by the Chinese remainder theorem[J]., 2014, 259: 495-502. doi: 10.1016/j.cam. 2013. 05.023.
[5] 崔涛, 刘培玉, 王珍. 前向安全的指定验证者(t, n)门限代理签名方案[J]. 小型微型计算机系统, 2014, 35(5): 1061-1064.
CUI Tao, LIU Peiyu, and WANG Zhen. Forward secure (t,n) threshold proxy signature scheme with designated verifier[J]., 2014, 35(5): 1061-1064.
[6] 张文芳, 王小敏, 郭伟, 等. 基于椭圆曲线密码体制的高效虚拟企业跨域认证方案[J]. 电子学报, 2014, 42(6): 1095-1102. doi: 10.3969 /j.issn.0372-2112.2014.06.010.
ZHANG Wenfang, WANG Xiaomin, GUO Wei,. An efficient inter-enterprise authentication scheme for VE based on the elliptic curve cryptosystem[J]., 2014, 42(6): 1095-1102. doi: 10.3969/j.issn.0372-2112.2014.06.010.
[7] HERZBERG A, JAKOBSSON M S, JARECKI H,. Proactive public key and signature systems[C]. Proceedings of the 4th ACM Conference on Computers and Communication Security, Zurich, Switzerland, 1997: 100-110.
[8] JARECKI S and SAXENA N. Further simplifications in proactive RSA signature schemes[C]. Proceedings of TCC’05, Massachusetts, USA, 2005: 510-528.
[9] FRANKEL Y, GEMMELL P, MACKENZIE P D,. Proactive RSA[C]. Proceedings of CRYPTO’97, California, USA, 1997: 440-454.
[10] RABIN T. A simplified approach to threshold and proactive RSA[C]. Proceedings of CRYPTO’98, California, USA, 1998: 89-104.
[11] FRANKEL Y, MACKENZIE P D, and YUNG M. Adaptive security for the additive-sharing based proactive RSA[C]. Proceedings of PKC’01, Cheju Island, Korea, 2001: 240-263.
[12] ALMANSA J F, DAMGARD I, and NIELSEN J B. Simplified threshold RSA with adaptive and proactive security[C]. Proceedings of EUROCRYPT 2006, Saint Petersburg, Russia, 2006: 593-611.
[13] LUO H, KONG J, ZERFOS P,. URSA: Ubiquitous and robust access control for mobile ad hoc networks[J]., 2004, 12(6): 1049-1063. doi: 10.1109/TNET.2004.838598.
[14] FRANKEL Y, GEMMELL P, MACKENZIE P D,. Optimal-resilience proactive public-key cryptosystems[C]. Proceedings of the 38th Symposium on Foundations of Computer Science (FOCS), Miami Beach, USA, 1997: 384-393.
[15] JARECKI S and SAXENA N. On the insecurity of proactive RSA in the URSA mobile ad hoc network access control protocol[J]., 2010, 5(4): 739-749.doi: 10.1109/TIFS.2010. 2058104.
[16] SHOUP V. Practical threshold signatures[C]. Proceedings of EUROCRYPT 2000, Bruges, Belgium, 2000: 207-220.
[17] ZHOU L and HAAS Z J. Securing Ad hoc networks[J]., 1999, 13(6): 24-30.
Proactive Threshold RSA Signature Scheme Based on Polynomial Secret Sharing
XU Fu
(PLA Information Engineering University, Zhengzhou 450002, China)(Information Technology Institute of Beijing City, Beijing 100094, China)
All the existing provable secure proactive threshold RSA signature schemes rely on additive secret sharing, in which all players have to cooperate to produce a signature, valid players’ secret shares may be exposed, and the computing efficiency is too low. Based on Shoup’s threshold RSA signature scheme, a proactive threshold RSA signature scheme is proposed by usingpolynomial secret sharing, and its security and practicability are analyzed. Results show that the proposed scheme is unforgeable and robust under the model of static mobile adversary, and compared with the existing comparable schemes, its communication overhead is lower and computing efficiency is higher.
Threshold signature; RSA; Polynomial secret sharing; Proactiveness
TP309
A
1009-5896(2016)09-2280-07
10.11999/JEIT151164
2015-10-21;
2016-06-06;
2016-07-19
国家科技重大专项(2012ZX03002003)
The National Science and Technology Major Project of China (2012ZX03002003)
徐甫 xuphou@163.com
徐 甫: 男,1983年生,博士生,研究方向为信息安全.
