基于改进离散蜂群算法的车辆路径问题求解

姜 婷



基于改进离散蜂群算法的车辆路径问题求解

姜 婷1,2

(1.安徽经济管理学院 信息工程系，安徽 合肥 230059；2.合肥工业大学 管理学院，安徽 合肥 230009)

采用一种改进的人工蜂群算法(IABC)求解标准车辆路径问题. 针对基本人工蜂群算法易陷入局部极小、收敛较慢等缺陷，提出了6种邻域生成策略，并基于此设计了新的局部搜索算法. 引领蜂和跟随蜂根据该算法在邻域空间内更新当前解. 通过小规模和大规模算例的仿真实验，将本文算法与其它智能算法以及基本人工蜂群算法进行了比较，验证了本文提出的算法无论在有效性还是稳定性上都具有良好的效果.

车辆路径问题；离散蜂群算法；邻域生成策略；局部搜索算法

随着我国经济进入新常态，电子商务和物流业迎来了新一轮的发展机遇，物流配送是其中的重要环节. 车辆路径问题(Vehicle Routing Problem, VRP)是这一环节中非常关键的研究内容，属于组合优化领域和运筹学研究的热点和重点. 该问题是一个NP难题，问题规模较大时只能求得近似解，可以采用群智能优化算法进行求解. 很多学者在这方面取得一定的研究成果，如文献[1][2]采用粒子群算法，文献[3][4][5]采用遗传算法，文献[6][7][8]采用蚁群算法分别研究了物流配送中的车辆路径问题.

人工蜂群算法(Artificial Bee Colony Algorithm, ABC)由Karboga等模拟工蜂的采蜜行为提出[9]. 该算法参数较少、鲁棒性强、编码较简单，适用于绝大多数的目标优化问题[10-12]. 已有的研究表明，基本人工蜂群算法存在一些不足，如容易陷入局部极小、收敛较慢等[13]. 近几年，有学者将人工蜂群算法应用于车辆路径问题的求解中. 比如文献[14]采用改进了迭代策略和邻域构成的人工蜂群算法来求解最优路径选择；文献[15]提出了一种基于大规模邻域搜索的改进人工蜂群算法来求解带载重量限制的车辆路径问题；文献[16]采用基本人工蜂群算法对车辆路径问题进行了求解. 本文在已有研究基础上，提出了一种新的邻域构成方法，采用改进的蜂群算法(Improved Artificial Bee Colony Algorithm, IABC)求解标准车辆路径问题. 实验表明，本文提出的算法具有较快的收敛速度，并且能够稳定地得到车辆路径问题的可行解.

1 车辆路径问题的数据模型

标准的车辆路径问题一般是指带装载限制的车辆路径问题(Capacitated VRP，CVRP)，该问题可描述为：从某物流配送中心出发，使用辆车向个客户送货. 每个车辆载重为，每个客户的需求为，客户到客户的距离为，要求合理安排车辆配送路线， 使配送中心行驶距离最短. 定义变量：；. 则标准VRP数学模型[4-5]可描述如下：

其中公式(1)为目标函数，即所有车辆行驶距离最小；公式(2)保证每条配送路线上客户需求总量不超过每一台车辆的运载能力；公式(3)保证每一个客户只能被访问一次；公式(4)保证每个客户只被一辆车服务；公式(5)用来消除子回路；公式(6)和(7)表示变量的取值范围.

2 人工蜂群算法及其改进

2.1 基本人工蜂群算法

人工蜂群算法是群智能优化算法的一种，主要包含了蜜源和蜂群两个核心要素. 蜜源的位置对应于优化问题的可行解，其质量好坏由适应度决定. 蜂群包括引领蜂、跟随蜂和侦察蜂三种类型. 其中，引领蜂与蜜源一一对应，并以一定概率向其它蜜蜂分享蜜源的相关信息；跟随蜂根据引领蜂分享的信息选择一个蜜源，蜜源适应度越高，跟随蜂选择该蜜源的概率P越大；引领蜂和跟随蜂在所处蜜源的邻域内搜索新蜜源，如果新蜜源好于原来蜜源则替换之，否则保留原来蜜源；如果蜜源经次搜索未发生改变，则相应蜜蜂转换成侦察蜂，该侦察蜂将随机产生新的蜜源位置.

跟随蜂选择蜜源的概率公式如下：

其中，为蜜源个数，为第个蜜源的适应度.

引领蜂和跟随蜂的邻域搜索公式为：

2.2 邻域生成策略

基本人工蜂群算法与其它智能算法一样，在求解复杂问题时表现出收敛能力不足、易陷入局部最优等缺点. 为克服这些缺点，同时考虑到本文求解的车辆配送路径问题的离散特性，本文在文献[17-18]基础上提出了6种邻域生成策略，引领蜂、跟随蜂随机选择其中的一种策略更新解，描述如下：

1)交换邻域生成策略(One SWAP)，记为1：将原始解内两个位置数据进行互换；

2)前插邻域生成策略(One INSERT)，记为2：将原始解内某一位置的数据取出并插入到新的位置；

3)倒转邻域生成策略(One INVERSE)，记为3：将原始解内两个位置之间的所有数据逆序排列；

4)两次交换邻域生成策略(Two SWAPs)，记为4：原始解执行两次交换策略(One SWAP)；

5)前插邻域生成策略(Two INSERTs)，记为5：对原始解执行两次前插策略(One INSERT)；

6)倒转邻域生成策略(Two INVERSEs)，记为6：对原始解执行两次倒转策略(One INVERSE).

2.3 局部搜索算法

为了提高收敛能力、避免算法陷入局部最优，本文基于上述的邻域生成策略构建了新的局部搜索算法，用于引领蜂和跟随蜂更新解的过程中. 算法步骤如下：

焊接检验是通过采用调查、检查、度量、试验和监测等方法，把产品的焊接质量同其使用要求不断相比较的过程。目前在工业生产中所应用的焊接检验方法主要包括破坏性检验、非破坏性检验和声发射三大类。

1)建立一个指定长度的邻域列表(NeighborList NL)，如表1所示. 设原始解为，其邻域列表长度为，邻域生成策略. 邻域列表中的每行数据是对原始解随机选择生成策略产生，直到填满该列表，每行数据为一个新解.

2)计算邻域列表所有新解的适应度，选择适应度最高的新解与原始解比较. 如果大于原始解，则用适应度最高的新解替换原始解，反之则保持原始解不变.

3 求解车辆配送路径问题的人工蜂群算法

3.1 问题编码

本文采用自然数的编码方式[5]. 0表示配送中心，1～n表示客户. 每辆车从配送中心出发，最后返回配送中心，所以每辆车的运送路线以0作为开始和结束. 例如，对于有1个配送中心、6个客户、用2辆车完成配送任务的问题，可以用0-1-2-4-0-6-3-5-0表示一种配送方案. 即车辆1从配送中心出发，然后服务了客户1-2-4，最后返回配送中心；车辆2从配送中心出发，然后服务了客户6-3-5，最后返回配送中心.

3.2 本文采用的改进人工蜂群(IABC)算法

1) 设置算法基本参数，主要包括食物源规模、最大迭代次数和算法终止条件；

2) 随机初始化蜂群，计算每只蜜蜂对应的适应度；

3) 引领蜂根据本文2.3部分设计的局部搜索算法产生新解，如果邻域列表中所有新解的最大适应度优于原解适应度，则替换之，否则保持原解不变；

4)根据公式(8)计算跟随蜂选择蜜源的概率，然后根据本文2.3部分设计的局域搜索算法邻域范围产生新解，如果邻域列表中所有新解的最大适应度优于原解适应度，则替换之，否则保持原解不变；

6)记录到目前为止适应度最高的解；

7)判断是否满足终止条件，如果满足则输出最优解，算法结束，否则转步骤3.

4 算例验证及结果分析

为验证本文算法的有效性，本文以Matlab R2013a为开发环境，采用Intel Core i3 2.6GHZ、4GB的PC机，操作系统为Win7.

4.1 小规模算例

采用文献[3][5][16]选用的测试数据. 该实例描述如下：1个配送中心、8个客户数、2辆车. 每辆车载重量为8吨，每个客户点的需求量以及客户点与配送中心的距离详见文献[3]，要求合理安排车辆行驶路线， 使所有车辆总的行驶距离最小.

实验参数设置如下：种群规模设置为60，最大迭代次数为50，邻域列表长度为5，算法运行20次. 实验结果表明，本文算法每次运行都能得到最优解67.5，得到最优解所需迭代次数和需要花费的时间如表2所示. 此外，将相同种群规模和迭代次数的该实例采用不同算法运行的结果如表3所示，算法包括：标准遗传算法(GA) 和双种群遗传算法(DPGA)[19]、混合遗传算法(HGA)[20]、改进微粒群算法(MPSO)[1]、标准人工蜂群算法(ABC)[16]和本文算法.

由表3中的数据比较可以看出，在种群规模和迭代次数一致的前提下，本文提出的算法的无论从稳定性、可靠性还是速度方面都优于表中所列的其它算法. 人工蜂群算法作为一种新型的群智能优化算法，在求解车辆配送路径方面有一定优势，仍存在易陷于局部最优等缺陷. 基本人工蜂群算法中加入局部搜索优化后，该缺陷得到了一定改善，求解效果和效率都得以提升.

4.2 大规模算例

上述实例规模较小，不能有效验证算法对较大规模问题的适用性. VRP LIB是国际上通用的测试VRP问量的算例库，可用来检验算法的有效性与性能，在此，选用其中两个较大规模车辆路径问题基准测试算例：E-n22- k4.vrp(1个配送中心、21个客户、4辆车、最优解为375)和E-n33-k4.vrp(1个配送中心、32个客户、4辆车、最优解为835)进行仿真实验. 实验结果如表4所示. 表4中改进遗传算法实验数据来自文献[4]，人工蜂群算法实验数据来自文献[16]. 每个算法运行10次. 图1为算例E-n22- k4采用三种算法在不同种群规模和迭代次数下的收敛情况比较图.

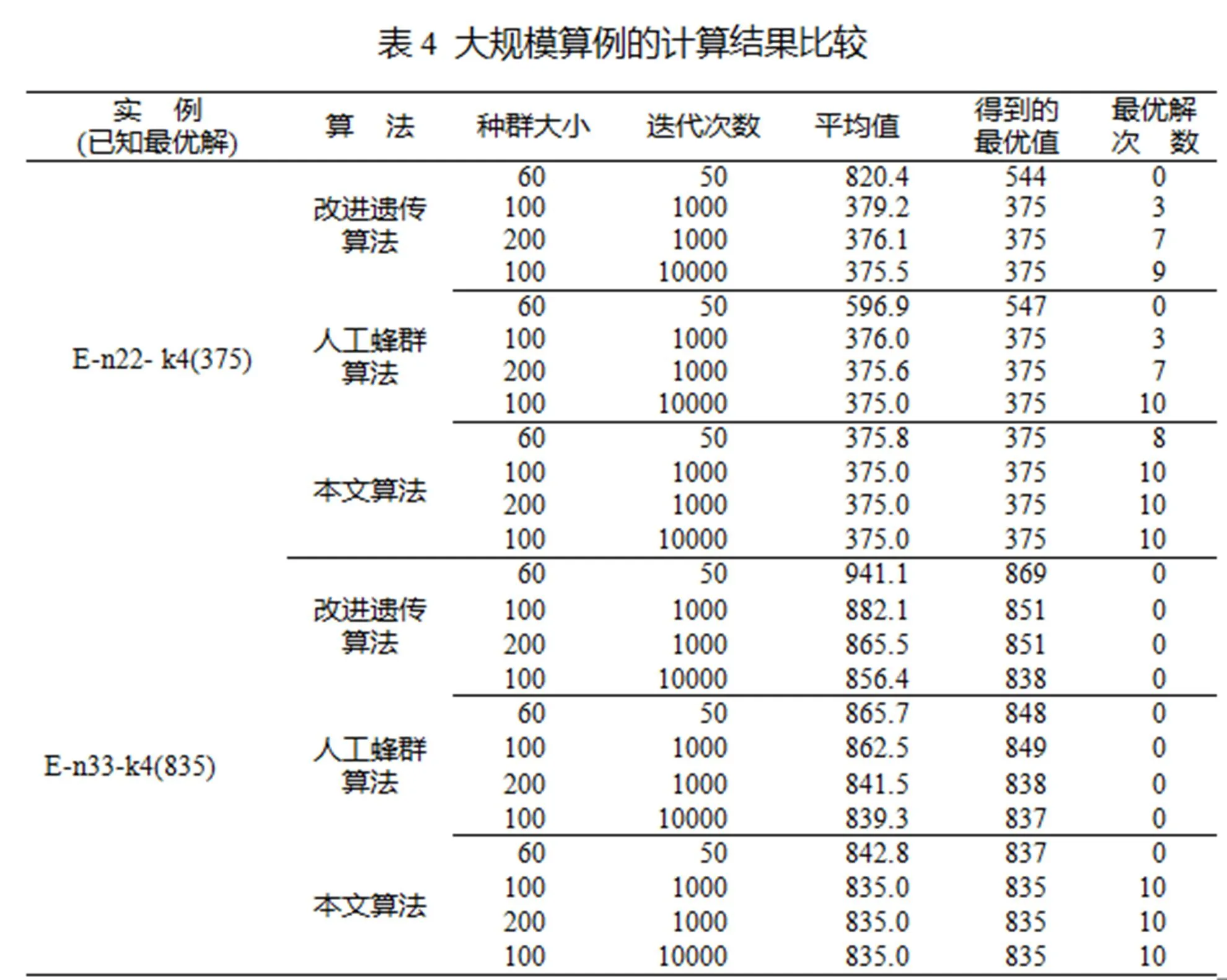
从表4的数据可以看出，种群和迭代次数越小，不同算法之间的效果差异越明显；种群规模和迭代次数越大，相同算法得到解的质量越高；当种群和迭代次数都增大到一定值时，二者对运行结果的影响变小. 本文算法在这两个算例下仍然保持了较好的有效性、稳定性和较高的运算效率. 在种群规模较小，迭代次数较少的情况下，本文算法相较另两种算法的优势更加明显，这意味着在计算资源较少和时间较紧的情况下，本文算法的有效性更高.

比较算例E-n33-k4和算例E-n22- k4的运行结果，前者比后者客户数增加了11，即问题规模增大，搜索空间相应增大. 此时，改进遗传算法和基本人工蜂群算法即使增大种群规模和迭代次数，效果也并不明显(如得到最优解的次数为0). 其原因是VRP属于NP-Hard问题，客户数增加导致搜索空间急剧增大. 本文算法由于设计了较为合理的邻域结构，提高了算法的收敛速度，同时避免了早熟，因而能在问题规模增大时仍能得到较优的求解效果.

从图1中可以看出，本文算法在不同种群规模和迭代次数中都可以稳定地得到较优的解. 没有邻域优化的基本蜂群算法相较于改进遗传算法，求解结果也有一定的优势. 实验结果验证了文献[9][13]的结论，即人工蜂群算法因其较好的全局搜索能力等特点，在求解优化问题相较于其它智能算法更具有竞争力. 同时，人工蜂群算法的开发能力较弱，需要构建较为合理的邻域搜索策略，以提高其局部寻优速度.

5 结语

本文提出了一种改进的离散人工蜂群算法，用于求解车辆配送路径问题. 为避免基本人工蜂群算法收敛速度较慢和陷入局部最优等问题，设计了新的邻域生成策略和局部搜索算法，用于更新引领蜂和跟随蜂的原始解. 通过小规模和大规模算例的实验，验证了本文算法的有效性和稳定性，以及人工蜂群算法在车辆配送路径问题求解中运用局部搜索算法进行优化的必要性.

[1] 肖健梅, 李军军, 王锡淮. 求解车辆路径问题的改进微粒群优化算法[J]. 计算机集成制造系统, 2005, 11(4): 577-581.

[2] 刘 娜, 雷秀娟. 免疫PSO算法求解多库房带时间窗VRP[J]. 计算机工程与应用, 2010, 46(5): 236-239.

[3] 刘芳华, 赵建民, 朱信忠. 基于改进遗传算法的物流配送路径优化的研究[J]. 计算机技术与发展, 2009, 19(7): 83-86.

[4] 周生伟, 蒋同海, 张荣辉. 改进遗传算法求解VRP问题[J]. 计算机仿真, 2012, 30(12): 140-143, 157.

[5] 周艳聪, 孙晓晨, 余伟翔. 基于改进遗传算法的物流配送路径优化研究[J]. 计算机工程与科学, 2012, 34(10): 118-122.

[6] 张泽彬, 郝志峰, 黄 翰, 等. 求解车辆路径问题的多邻域下降搜索蚁群优化算法[J]. 南京大学学报: 自然科学版, 2012, 48(1): 91-98.

[7] 孙 晶, 白艳萍. 改进的混合型蚁群算法在VRP问题中的应用[J]. 黑龙江大学自然科学学报, 2014, 31(3): 328-334.

[8] 徐洪丽, 钱 旭, 岳 训, 等. 一种新的基于logistic混沌映像的自适应混沌蚁群优化算法求解动态车辆路径问题[J]. 计算机应用研究, 2012, 29(6): 2058-2060.

[9] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri: Eroiyes University, 2005.

[10] SINGH A. An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem[J]. Applied Soft Computing, 2009, 9(2): 625-631.

[11] PAN Q K, TASGETIREN M F, SUGANTHAN P N, CHUA T J. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J]. Information Sciences, 2010, 181(12): 2455-2468.

[12] XU CHUNFAN, DUAN LLAIBIN. Artificial bee colony optimized edge potential function approach to target recognition for low-altitude aircraft[J].

Pattern Recognition Letters, 2010, 31(13): 1759-1772.

[13] AKAY B, KARABOGA D. A Modified artificial for real-parameter optimization[J]. Information Sciences, 2012, 192(6): 120-142.

[14] 张 涛, 陈 忠, 吕一兵. 求解最短路径问题的一种改进的人工蜂群算法[J]. 青海师范大学学报: 自然科学版, 2013(1): 5-7, 13.

[15] 林镇泽. 求解双层车辆路径问题的改进人工蜂群算法[D]. 广州: 华南理工大学, 2014.

[16] 王志刚, 夏慧明. 求解车辆路径问题的人工蜂群算法[J]. 计算机工程与科学, 2014, 36(6): 1088-1094.

[17] 桑红燕, 高 亮, 李新宇. 求解批量流水线调度问题的离散蜂群算法[J]. 中国机械工程, 2011, 22(18): 2195-2202.

[18] LI X, YIN M. A discrete artificial bee colony algorithm with composite mutation strategies for permutation flow shop scheduling problem[J]. Scientia Iranica, doi:10.1016/j.scient.2012.10.034: 1921-1935.

[19] 赵燕伟, 吴 斌, 蒋 丽, 等. 车.辆路径问题的双种群遗传算法求解方法[J]. 计算机集成制造系统, 2004, 10(3): 303-306.

[20] 姜昌华, 戴树贵, 胡幼华. 求解车辆路径问题的混合遗传算法[J]. 计算机集成制造系统, 2007, 13(10): 2047-2052.

(责任编辑：陈 丹)

Solving Vehicle Routing Problem by an Improved Artificial Bee Colony Algorithm

JIANG Ting1, 2

(1. Department of Information Engineering, Anhui Economic Management College, Hefei 230059, China;2. School of Management, Hefei University of Technology, Hefei 230009, China )

In this paper, we use an improved artificial bee colony algorithm(IABC)for solving standard vehicle routing problem. In order to avoid slow convergence and local optimum, we propose six neighborhood generating strategies. Meanwhile, we design a new local search algorithm based on the strategies. The leader bees and follower bees update the current solution in the neighborhood by this algorithm. Through the simulation experiment of large and small scale examples, the proposed algorithm was compared with some intelligent optimization algorithms and the basic artificial bee colony algorithm. Experimental results show that the proposed algorithm has good performance in both effectiveness and stability.

Vehicle routing problem; Improved artificial bee colony algorithm; Neighborhood generating strategy; Local search algorithm

TP391

A

2095-4476(2016)02-0009-06

2016-02-20;

2016-02-29

安徽省哲学社科规划项目(AHSKY2015D71); 安徽省社科创新发展研究课题(A2015020); 安徽省高校优秀青年人才基金重点项目(2013SQRL111ZD)

姜 婷(1976— ), 女, 安徽滁州人, 安徽经济管理学院信息工程系副教授, 合肥工业大学管理学院博士研究生, 主要研究方向: 决策支持系统, 群体智能.