一个超混沌纠缠系统的动力学分析

魏炎炎，杨淑菊



一个超混沌纠缠系统的动力学分析

魏炎炎，杨淑菊

(云南经济管理学院 工程学院，云南 昆明 650304)

采用正弦函数混沌纠缠的方法构造出一个新超Rabinovich混沌系统，绘制出其超混沌的吸引子，并对其进行动力学分析以验证这个系统是超混沌的．

超混沌系统；混沌纠缠；混沌吸引子；动力学分析

混沌系统作为非线性动力学与控制论等重要的交叉学科，在Lorenz系统的基础上，提取该混沌系统的机理及其复杂的动力学特征，进而衍生出众多类似Lorenz系统，如超混沌系统对Lorenz系统及其衍生的Lorenz族系统的新分支的研究，具有重要的实际意义.

目前，建构新的人工混沌系统这个活跃的话题[1-7]成为趋势. 文献[3]提出一个新的名词——混沌纠缠，基本原理是通过纠缠函数纠缠两个或多个稳定的线性子系统来产生一个人造的混沌系统，本文利用混沌纠缠的方法建构出一个新的超混沌系统，并验证该系统是混沌的.

1 超混沌系统提出

采用一些非线性函数对系统纠缠，如果两个或及其以上的线性子系统能产生混沌行为，就叫混沌纠缠．其中纠缠函数就是上述的非线性函数．

现考虑两个线性子系统，一个是三维系统，另一个是一维系统，如下：

现采用正弦函数来纠缠(1) 及线性化，再和(2)系统组合起来，得到如下的系统

其中，,,,,,是纠缠系数，且均大于零；sin()，sin()，sin()是纠缠函数. 当=2,=4,=4,=4,=1,=1时，有一个超混沌吸引子出现，相图如图1，相图如图2所示.

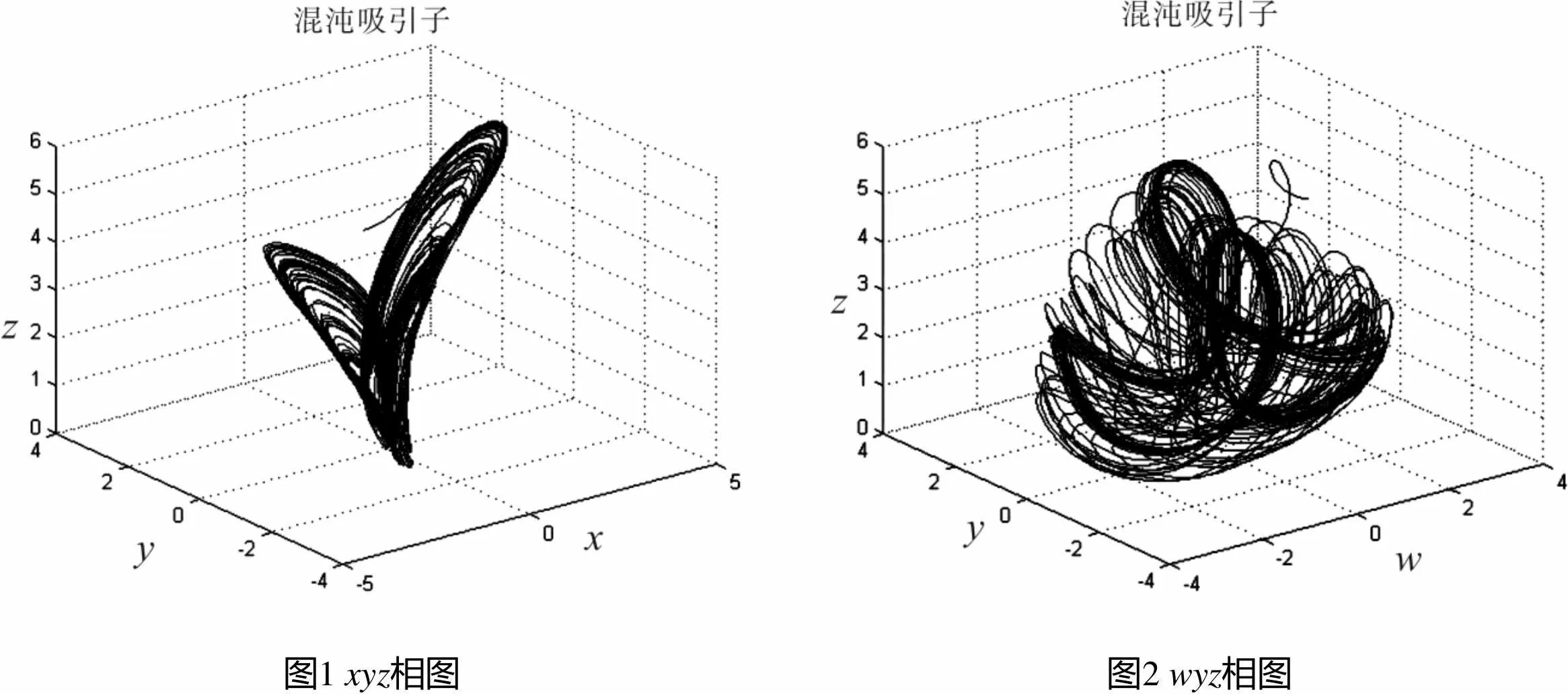
图1 xyz相图图2 wyz相图

2 系统混沌性

2.1对称性和不变性

现分析系统(3)，系统(3)具有自然对称性，对系统(3)做如下变换：

()®()

即在变换()®()下，对所有的参数,,,,,具有不变性，若+()是系统(3)的平衡点，则()一定也是系统(3)的平衡点；如果()是系统(3)的一条轨道线，那么()也是系统(3)的轨道线.

2.2 耗散性和吸引子的存在性

现作系统(3)的向量场散度

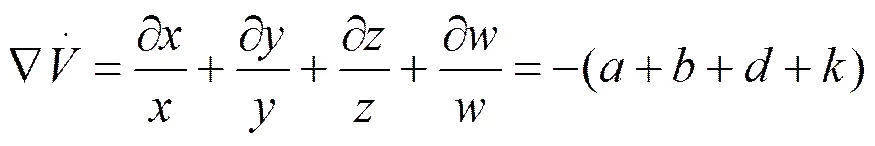
当+++>0时，系统(3)具有耗散性，且收敛到． 即一个为0的初始体积元，在时间时收敛为，当®¥时. 包含系统轨线的每个体积元都收缩到0．所有轨线限制在一个体积为零的极限子集上，系统的渐近行为会被固定到一个吸引子上，从而存在吸引子．

2.3 有界性

以上述对四维超Rabinovich纠缠系统的生成为基础，对系统(3)有界性的分析．

定理1 当,,,>0，系统(3)是有界的.

2.4 平衡点的稳定性

在所,,,,,均大于零的状态下，原点是(3)系统的平衡点，且是唯一的．系统(3)在0=(0, 0, 0, 0)处的Jacobian矩阵，其特征值方程为

由于存在=-，.

则得到其罗斯-霍维兹判别行列式为

则在平衡点0=(0, 0, 0, 0)是渐进稳定.

3 结论

本文是采用正弦函数混沌纠缠的方法，衍生出一个新超Rabinovich混沌系统，并利用Matlab软件绘制超混沌的一个吸引子，分析该超混沌系统的对称性、不变性、耗散性、吸引子的存在性、有界性、平衡点的稳定性等混沌特征，从而验证了这个系统是超混沌的. 对于混沌系统衍生模型，其动力特征的多样性及其复杂性，有待进一步深化.

[1] 刘秉正, 彭建华. 非线性动力学[M]. 北京: 高等教育出版, 2004: 120-131.

[2] 陈关荣, 金 虎. Lorenz系统族的动力学分析、控制与同步[M]. 北京: 科学出版社, 2003: 9-25.

[3] 熊诗波. 机械工程测试技术基础[M]. 北京: 机械工业出版社, 2008: 60-62.

[4] 张晓蓉, 吴成茂, 李文学. 基于多涡卷 Jerk-Chua 混沌和自编码的扩频码构造方法[J]. 系统工程与电子技术, 2015, 37(4): 936-941.

[5] 刘龙生, 康云莲, 赵俊玲. 广义符号动力系统中的Li-Yorke混沌集和ω-混沌集[J]. 广西师范大学学报:自然科学版, 2014, 32(2): 75-81.

[6] 魏炎炎. 超Rabinovich系统混沌现象及混沌同步的研究[D]. 西安: 西安建筑科技大学理学院, 2012.

[7]. Feedback and adaptive control and synchronization of a set of chaotic and hyperchaotic systems[J]. Chaos, Solitons & Fractals, 2007, 32(4): 1572-1582.

(责任编辑：饶 超)

Dynamical Analysis of a Hyper Chaos Entanglement System

WEI Yanyan, YANG Shuju

(School of Engineering, Yunnan College of Business Management , Kunming 650304, China)

A new hyper Rabinovich chaotic systems is proposed in this paper ,which adopts the method of sine function chaos entanglement. Then, it draws one attractor of the hyper system and analyzes the dynamical phenomena to finish the studies of phenomena of hyper chaos.

Super chaotic systems; Chaos entanglement; Chaotic attractor; Dynamical analysis

O415.5

A

2095-4476(2016)02-0019-03

2015-10-12

魏炎炎(1984— ), 女, 湖北随州人, 云南经济管理学院工程学院讲师.