对一道几何题证法的赏析与思考

杨昌义

对一道几何题证法的赏析与思考

杨昌义

一位勤学的学生问了我八年级上册某教辅资料上的一道题，题目是：已知：如图1，在△ABC中，AB=AC，点E在CA的延长线上，∠E=∠AFE。求证：EF⊥BC。

教科书上两直线垂直的定义是：两直线相交所成的四个角中，如果有一个是直角，那么这两直线叫做互相垂直。利用定义证明两直线垂直是基本的思维方法。但对刚学证明的学生来说，还是较为困难的。而本题待证的两条线段EF与BC不相交，更增加了难度。考虑到此题比较典型，我在接下来的课上将之作为例题给全班学生进行了详细的分析讲解，并板书了证明过程。

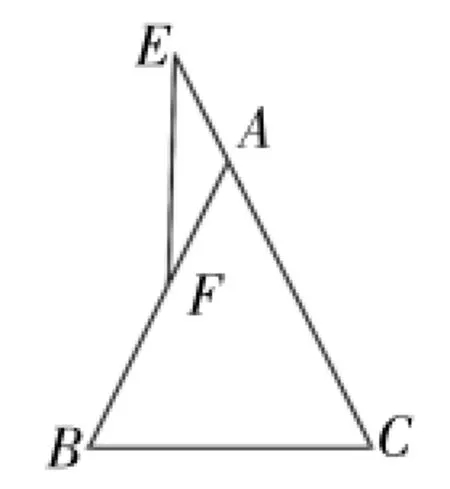
图1

证明：如图2，延长EF，交BC于G。因为∠BAC、∠EAF分别是△AEF和△ABC的外角，所以∠BAC=∠E+∠AFE，∠EAF=∠B+∠C。又因为AB=AC，所以∠B=∠C，且∠E=∠AFE，所以∠BAC=2∠E，∠EAF=2∠C。而∠BAC+∠EAF=180°，所以2∠E+2∠C=180°，所以∠E+∠C=90°，则∠EGC=180°-（∠E+∠C）=90°，所以EG⊥BC，即EF⊥BC。

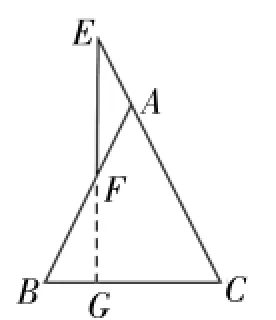
图2

我是利用三角形外角定理以及平角的定义得到∠E+∠C=90°，再利用三角形内角和定理得到∠EGC=90°，从而得到结论。这一证明方法层次清晰，学生很容易理解和掌握。随后，我让大家思考有没有别的证法。

大家一番沉思后，反应敏锐的生1给出了新的证法。

证法1：如图3（1），过点B作BD∥EF，交CA的延长线于D。则有∠D=∠AEF，∠ABD=∠AFE。因为已知∠AEF =∠AFE，所以∠D=∠ABD。又因为AB=AC，所以∠ABC=∠C。在△DBC中，因为∠D+∠DBC+∠C=180°，即∠D+∠ABD+∠ABC+∠C=180°，也即2∠ABD+2∠ABC=180°，所以∠ABD+∠ABC=90°，即∠DBC=90°，所以DB⊥BC。因为EF∥DB，所以EF⊥BC。

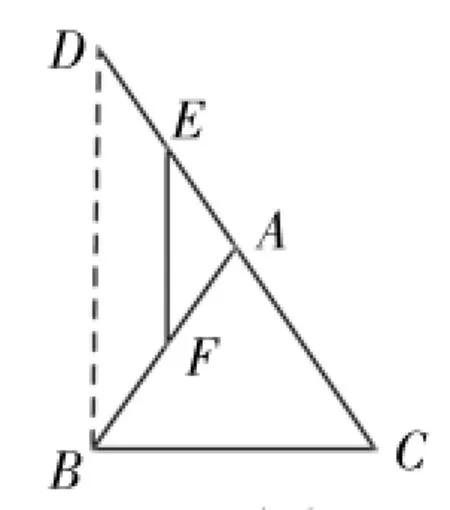
图3（1）

赏析：此证法值得称道的有两点。第一，学生能灵活地将辅助线作到了已知图形的外部，富有创新思维。而且这么添作辅助线后，我们从宏观上可以将本题看作是从Rt△DBC衍生出来的一道题，给人以“一览众山小”之感。第二，这种证法不直接证明EF⊥BC，而是先证DB⊥BC，由BD∥EF间接得到EF⊥BC。这种思维对于初学证明的初中生来说也是一种创新，值得点赞！（当然，此证法在得出∠D=∠ABD后，有AD=AB。又由已知AB=AC，所以AB= AD=AC。由此得出∠DBC为直角则更为简捷，但此知识点湘教版安排在八年级下册第一章，此时学生们尚未学过）

谁知一石激起千层浪，受作平行线辅助线的启发，学生思维的闸门一下子打开，作出了如图3（2）～图3（4）的辅助线，其证法本质上与证法2相同。但这种发散性思维对初学证明的学生来说是非常可贵的，值得赞赏。

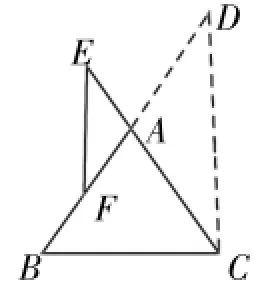
图3（2）

图3（3）

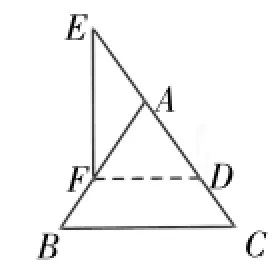
图3（4）

接着，喜欢独立思考的生2另辟蹊径，得到了新的证法。

证法2：如图4，过A作AG∥EF，交BC于G，则有∠E=∠CAG，∠AFE=∠BAG。因为∠E=∠AFE，所以∠CAG=∠BAG，即AG是∠BAC的平分线。又AB= AC，所以AG⊥BC。因为EF∥AG，所以EF⊥BC。

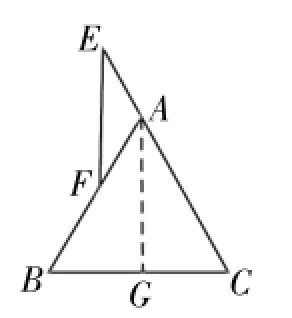
图4

赏析：此证法的思路与证法1类似，仍是利用“在同一平面内，一直线垂直于两平行线中的一条，必垂直于另一条”，但证明垂直时是利用等腰三角形“三线合一”性质完成的，不能不说是逻辑思维上一个创新的亮点，值得给他一个大大的赞！

受此启发，善于钻研的生3也想出一招，其证法如下。

证法3：如图5，过A作AD⊥EF于D。由于∠E=∠AFE，所以AE=AF，∠EAD=∠FAD。因为∠EAF=∠B+∠C，即∠EAD+∠FAD=∠B+∠C，而由AB=AC得∠B=∠C，所以2∠FAD= 2∠B，即∠FAD=∠B，所以AD∥BC。因为EF⊥AD，所以EF⊥BC。

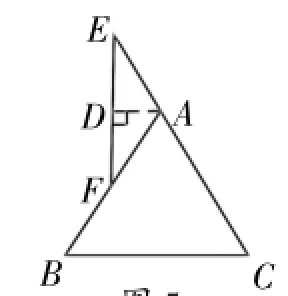
图5

赏析：此证法与上述证法思路实际上是一致的，但辅助线作法不同，作出的AD垂直于EF，再证AD与BC平行。这也算是一种新法吧，值得表扬！

思维活跃的生4又有了新法。她的证法是：

证法4：如图6，延长EF交BC于G，过点F作FH∥EC，交GC于H，则有∠GFH=∠E，∠FHG=∠C。而AB=AC，所以∠B=∠C，因此有∠FHG=∠B，△FBH是等腰三角形。

又∠E=∠AFE，所以∠GFH=∠AFE。而∠AFE=∠BFG，所以∠GFH =∠BFG，因而FG⊥BH，即EF⊥BC。

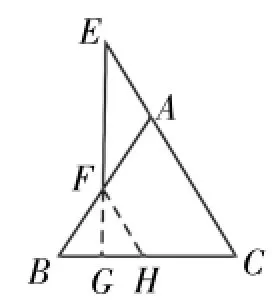
图6

赏析：此证法不仅直接证明EF⊥BC，也用等腰三角形“三线合一”性质来达到目的，实质上是上述各种方法的综合，既继承又发展，新颖别致，值得赞赏！这也是同学们之间合作交流的功劳。

见大家讨论得如此热烈，一向比较沉稳的生5坐不住了。他给出了自己的证法。

证法5：如图7，过点E作EG∥AB，交CB的延长线于G，则∠G=∠ABC，∠GEF=∠AFE。

因为AB=AC，所以∠ABC=∠C，所以∠G=∠C，△EGC为等腰三角形。又因∠AFE=∠AEF，所以∠GEF=∠AEF，EF是顶角∠GEC的平分线，所以EF⊥BC。

图7

赏析：这个证法尽管与证法4一致，但辅助线作得很妙，在原图形之外构造了一个大的等腰三角形，进而利用等腰三角形性质，使证明过程简捷而流畅。从宏观上看，本题也相当于是由等腰△EGC衍生出来的一道题目，使我们也有“登高远望”之感，确实值得点一个大大的赞！

下课了，学生们还兴致勃勃地切磋交流，想挖掘出更多更好的证法，教室里一片热烈的景象。我被学生活跃的思维和浓厚的探究氛围所感动。本节课，我只带领学生讨论了一道题，涉及的内容却如此丰富。学生们在交流各种证法的同时，规范了证明题的书写格式，训思维得到了发散，创新意识也被激发。要培养学生的解题能力，题目在精不在多，教师要结合教学的重点和难点，多选取具有启发性、典型性和规律性的题目。尤其要发挥一法多用和一题多解的作用，切实减轻学生的学业负担，充分激发学生的创新思维。

（作者单位：永州市柳子中学）