何处着手方能更善？——一次网络解题教学经历

陈永斌

何处着手方能更善？
——一次网络解题教学经历

陈永斌

平时，我喜欢利用QQ群跟学生讨论学习和人生，学生也非常喜欢这种交流形式。在他们看来，相遇在网络，暂时忘却了师生的角色，那种虚虚实实的感觉，在平常课堂上是无法体会得到的。于我来说，则可以通过网络化的教学方式，指引他们渐入会学习的佳境。

暑假的一个早晨，刚做完晨练回来，我习惯性地打开了电脑。“嘀嘀嘀——”企鹅图标闪动着它的身姿向我问好。“看看今天又有什么好消息。”我点开聊天界面，映入眼帘的是我的一个学生王桉福在群里传的一道题目：

当时，我认为这是一道极其简单的常规题，于是敲击键盘回复：“自己画图，然后很容易就算出来了。”接着就去吃早餐了。可是，我回到电脑前时，发现群里面讨论得沸沸扬扬。有很多学生抱怨道：“这图怎么画啊，万能的神啊？”学生有的画出如图1的 45°角，接着不知道该如何画，也有的估摸着画出AB=2（如图2和图3），但CD不知道如何求得。

图1

图2

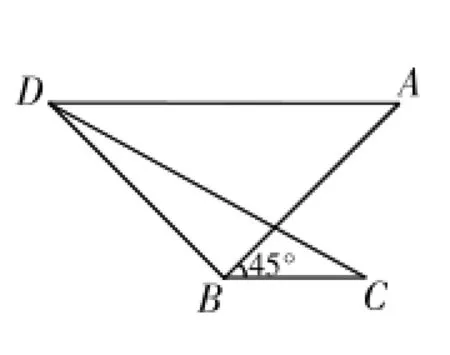
图3

就在大家一筹莫展的时候，平常不怎么说话的唐叠澜同学发言了：“这道题目的答案是无理数。哈哈，膜拜吧！”另一位同学廖一鸣问道：“你是怎么算的，别不是作业帮吧？”后面好几个同学也接着“飘”来疑惑的表情。此时，我估计作为课代表的唐靖同学该发言了。因为平时她最喜欢在大家的讨论陷入僵局时出现。果不其然，她指出了图2中BC与AD应该具备垂直这种特殊的位置关系。大家还在你一言、我一语的争论当中。群里的一位家长也积极发言，建议大家都先不要争，各自在自己的草稿纸上画图，把解题过程写在纸上，用手机拍了传上来进行比较。之后的几分钟，大家的QQ都一阵沉默。这时我的QQ又响起了，原来是王桉福同学想跟我视频。我接通了之后，只听他说道：“老师，这道题目其实我已经做出来了。在图2中，只要延长BC，交AD于点E，利用三线合一定理以及勾股定理就可以解出CD=。在图3中，只要过点C作DB的垂线，交DB的延长线于点E，就可以利用含45°角的等腰直角三角形三边的特殊比例关系以及勾股定理求出CD=。”

我听了后感到很是安慰。因为他熟练地运用了学过的基本几何模型，而且会构造辅助线顺利解决数学问题，表达也非常清楚。

其实，在他们讨论的时候，我在网上搜索出，本题是2013年哈尔滨中考试卷中的一道填空压轴题。网络上只有答案而没有过程。但在电脑屏幕前，我不能让他感觉到我的喜悦。对他这类数学基础比较好的学生来说，经历解题的过程，帮他们养成反思归纳的意识，比解出题目本身更重要。于是，我问道：“这道题从什么地方开始画才更有利于解题呢？”他停顿了一下，没想到我并没有表扬他，而是要求他做进一步的思考。此时我也没闲着，迅速地调出了几何画板软件，做起了动态演示，把每个过程通过QQ里面的截图功能即时展现给群里的学生观察（如图4、图5和图6）。

图4：先作出等腰直角三角形ABD。

图5：再作∠ABC =45°，有两种情况。

图6：连接CD，有两种情况。

群里的学生很快意识到，原来先画等腰直角三角形ABD可以较容易地找到本题的切入点，分类也更清晰。王桉福同学也在群里发表感叹：“原来先画基本图形可以更快地找到解题思路。开始我先画∠ABC =45°，画了好久才找到思路。经唐靖同学提醒BC与AD垂直，我才最终解决这道题。按老师这种画法就更容易上手了。”此时，我抓住时机，引导学生通过百度搜索出2015年哈尔滨中考试卷中一道类似的题目：

在矩形ABCD中，AD=5，AB=4，点E，F在直线AD上，且四边形BCFE为菱形，若线段EF的中点为点M，则线段AM的长为_____。

我要求他们动手实践，画出图形的同学可以单独与我视频，必须说出画图的过程。我在数学语言上帮他们进行规范，而解题过程则在QQ群内进行展示，同学们都可以参与评价。为了帮助那些还没有完全搞懂这类题目作图方法的同学加深理解，我在此之后做了一节微课《据题作图，依图析题》，上传到QQ群，供学生们观看（如图7、图8、图9）。

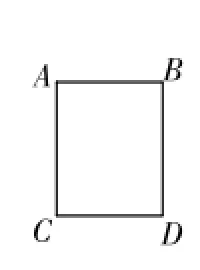
图7

图8

图9

在这个事件中，那位不怎么爱说话的同学数学基础并不好，但他能够利用网络搜索资料，虽然不求甚解，但作为网络时代的原住民，他的信息应用能力是毋庸置疑的。若引导得法，还是能有进步的。王桉福同学在大家都给前面这位同学白眼的时候能给予鲜花，唐靖同学毫无保留地展示自己的思路，又让我看到了学生之间的互助之情，家长主动参与学生的QQ群学习讨论，更让我看到了家庭教育与学校教育无缝对接的可能性。教师根据学生的学习需要适时安排教学内容，采用合理的知识呈现方式以及课堂组织形式，课后又能生成学习资源，体现了新时代教师应有的学科以及信息素养。

（作者单位：永州市冷水滩区京华中学）