对二年级数独教学的思考与实践
2016-10-13熊坤云
熊坤云
对二年级数独教学的思考与实践
熊坤云

一、初次实践,发现问题
下图所示是二年级下册“推理”中的例2。在教学时,可分三步引导学生进行推理。

第一步:观察A的位置,A所在的行和列,已经出现了1、2、3,则A不可能是1、2、3,只能是4。
第二步:A是4,B所在的行和列已经出现了2、3、4,所以B只能是1。
第三步:利用上述方法,推理出其他数,完善表格。
然而我在教学过程中发现,学生还是有点云里雾里。学生的学习障碍有以下四点。
1.学生在一年级学习的是有规律的一维表格填数游戏,即在某一行或某一列进行填数,而此例题是多行和多列的方阵表格,思维的跳跃性大,学生不能很快将行和列结合起来进行综合的分析与思考。
2.在题意不明、规则不清的情况下,学生容易将幻方与数独混为一谈。
3.找不出首先要填写的空格位置。让学生从某一行或列确定3个数,找出最后一个数是容易的。但是,当面对4×4的十几个方格的数独,到底哪一个空格所在的行和列已经出现了3个不同的数,学生感到很茫然。
4.不能用简洁、有条理的语言表述推理过程。
二、透过问题再思考
数独的教学该如何定位,如何展开才能引导学生推理呢?纵观二年级下册教材,“数学广角”这一单元的教学内容是简单推理,其编排目的主要是借助贴近学生的素材,让学生在活动中感受推理过程。教材内容的呈现符合螺旋上升的原则,其中例1是原实验教材的例3,例2“数独”是新增的内容。
其实,数独是训练观察能力和推理能力的游戏,推理方法多种多样。教材中介绍的是“唯余法”,即“利用空格所在的行和列已经出现了3个不同的数,只剩下唯一的数,进而确定空格只能填几”。这与例1的推理思想“不是……而是……”密切相联。然而,玩数独常用的方法是唯一法和排除法。相对“唯余法”而言,这两种方法较简单。一般来说,只有在使用基本的排除方法都失效的情况下,才会用“唯余法”解题。为何教材要舍近求远,其用意何在?能不能就用孩子们熟悉的排除法解决问题呢?
虽然教材通过多种方式降低了题目的难度,但是学生理解这样的问题仍存在一定的难度。让学生综合、全面地分析问题并解决问题,对二年级的学生来说是比较困难的。那么,像教材上一样给出提示是否会禁锢学生的思维,限制学生自主探究的欲望呢?如果真正放手让孩子自己玩数独,他们又能否很快找到突破口?
有很多二年级学生在经历推理过程的学习后,能够心知肚明,会做题、会填空,却是心明口不明,说不出具体的推理过程。怎样培养学生用简洁的语言有条理地表达推理过程的能力呢?
《数学课程标准》提出学生要“在参与观察、实验、猜想、证明、综合实践等数学活动中,发展合情推理和演绎推理能力,清晰地表达自己的想法”。那么,如何设计有效的推理活动,让学生自己尝试、大胆猜想、小心验证,从而找到方法,确定结论?
三、带着问题再实践
基于教材编排及真实学情,笔者整合教材资源,对教材进行调整,舍弃例题,从3×3的方格入手,引导学生由浅入深地理解和掌握推理的方法,渗透推理思想。
1.巧设情境,激活经验
学生还没有系统学习行和列等位置的知识,综合观察力不强,没有同时看空格所在行和列的意识。因此,课始教师让学生找一找自己所在的行和列,以游戏方式进行,全体学生参与。凡是处于一个中心点所在的行和列的学生均站起来,其他学生进行观察、判断。看似简单有趣的生活情境,实质体现了数学与生活的联系,让学生置身其中,对“空格所在的行和列”感受深刻,理解到位,为找“已经出现的数”开好头。
2.初次探索,总结方法
解决三阶方格对学生来说不难,此时的关键是训练他们用简洁的语言进行表达的能力,并结合行和列同时观察,初步感知怎样寻找突破口。
教师出示三阶方格(如图1),逐步提问:先填哪个空格?填几?为什么填它?怎样确定它?
填完两空后,对单格的判断让学生明确了游戏规则,感知到已知数的作用,在此基础上结合行与列综合判断就必不可少了。
填完表格后,教师引导学生总结解决问题的经验和方法,进一步明确说理。
为了让学生快速寻找到突破口,更准确、清晰地运用简洁的语言进行推理,继续巩固三阶方格(如图2)。学生先自己动手填,然后同伴交流,说说自己是怎么推理的。
3.运用方法,尝试挑战
正式进入四阶方格(如图3),可以以猜数字的游戏形式,像捉迷藏一样,引导学生积极投入到游戏中来。
由三阶方格到四阶方格,数独游戏的难度是成几何倍数增长的。在实际填数过程中,并不是所有空格都能一步填出,必然有先后。前面三阶方格解决了填数的先后问题,学生能很快基于行和列进行推理并找出能确定的空格。随着空格背后的答案一一揭晓,学生也在不断提炼数独的玩法,领悟推理思想,感受数学之美。

图1
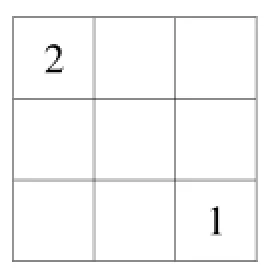
图2
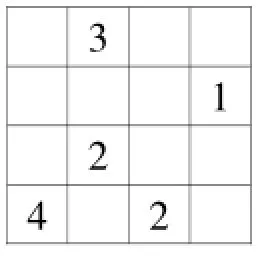
图3
4.意犹未尽,延伸课外
课末,教师出示数独王国的资料,介绍数独的来源,给学生看各种各样的变形数独,冲击学生大脑,激发学生思考,掀起新一轮的探究。在反复的实践应用中,学生逐步内化推理思想。
总之,推理这一数学思想方法的渗透不是一蹴而就的,数独只是一个载体。只有我们以生为本,根据学生的实际情况创造性地使用教材,准确定位,方能真正发挥数独的功效,实现推理思想的有效渗透。
(作者单位:湖南师范大学附属小学)
