分数教学研究报告

长沙市丁丽小学数学名师工作室潇湘数学教育工作室

分数教学研究报告

长沙市丁丽小学数学名师工作室潇湘数学教育工作室

小学阶段对分数教学的研究一直是个热点。无论是三年级的分数初步认识，还是五年级的分数再认识，抑或是六年级的分数乘除法及应用题的教学，都是一线教师及教学专家们研讨的重要内容。本文是我们在分数教学这一板块进行的一些研究尝试，试图在思考与实践层面均有所突破。

一、不可小看的分数

与自然数、小数的教学相比，分数无论是教还是学无疑都是比较难的。难在哪里？师生们的共同体会至少有这么四点。

1.分数“长”得就和别的数不一样。

孩子们的数学学习是从自然数（整数）开始的。后来接触的小数，是他们在数的认识里第一次数域的扩充。由于小数沿用整数的位值系统和十进制，很多教学问题可以通过整数知识的正向迁移得以克服。

引入分数是孩子数学学习过程中第二次数域的扩充。但无论是数的表现形式（书写）还是大小比较抑或是计算，分数都让孩子们觉得与之前所学的整数、小数太不一样，也就无法很好地从已学知识里获得足够多的经验来类比，从而造成了很多认知困难。

2.分数的意义多样。

张奠宙先生将分数的定义大致分为四种：

定义1（份数定义）：分数是把一个单位平均分成若干份之后其中的一份或几份。

定义2（商定义）：分数是两个整数相除（除数不为0）的商。

定义3（比定义）：分数是整数q与整数p（p≠0）之比。

定义4（公理化定义）：有序的整数对（p，q），其中p≠0。

如此丰富的内涵，对孩子来说，要能理解、掌握并能区分和应用，显然是个难题。唐彩斌老师（浙江省杭州市上城区教育学院）做过一个关于分数问题的研究。

3.分数教学中量与率难以区分。

这里有一道测试题：一根长2米的铁丝，将它平均分成5段，每一段是全长的（），每一段是（）米。学生的错误率之高让之成为经典检测题，一线教师看到这道题时都会会心一笑后再无奈一笑。

在分数教学中，对分数含义中量与率这两个方面的辨析是一个重难点。学生学习时总是因不得法而难以掌握，教师只得采用“分数后面是否带上单位”这一方法帮助学生进行区别，但是这种方法显得十分机械，难以让学生深入到含义层面的理解。

二、实例中找找难的源头

由上面的问题呈现我们可以看到，分数的难有其客观原因，即分数与生俱来就比之前学的数要难一些，同时也与教材编写和教学处理有关。

案例：对分数除法应用题的讲授，新教材回避了直接用除法的算术解法。比如这样一道题：甲数是乙数的，甲数是20，请问乙数是多少？这道题孩子能从等分意义上迅速找到答案是60，列式为20÷=60。至于列式为何用除法，一线教师讲得极其艰涩痛苦，孩子学得也非常困难。而对这一问题：甲数是乙数的3倍，甲数是90，乙数是多少？孩子会很轻松地列式并解说算理：求标准量（一倍量），用比较量（多倍量）除以倍数就可以了，即90÷3=30。对比一下这两道题，我们能反思到什么教学问题吗？很显然，倍与率是同一种数量关系。我们在三年级之前教学加减法都是基于差比的数量关系进行列式运算，三年级时为学习乘除法引入了倍比关系，并把乘除法与倍比关系从算法与算理两方面进行了对应。而引入分数之后，我们在教学分数的乘除法时竟然脱离了倍比运算的理解，取而代之的是我们研发的各种对算理的解释。如此看来，我们并没有保持原有的认知规律，把分数融入到原有数的系统中去认识，教材的呈现也没有保持原有的数的认识的编排。

如何解决这个问题？如何让分数的教学回到数的教学轨道上来？首先，所有的研究必须有一个共识：分数必须当作一类数来教！只有在一种正确的共识下，大家的研究才能垒土成台，而非散沙千里，才能有效，从而实现质的飞跃。很多专家和老师都作过尝试。比如分数意义的学习，有老师从率引入改为从量引入，然后进行量与率的对比，在此基础上进行数的抽象。还有老师从分数的其他意义切入，比如从商的定义入手教分数，做了很好的突破。大量的实践与反思让我们看到了教学改变之后学生身上发生的可喜改变。这些都是国内的研究交出的最新答卷。

数来自于数（shǔ）。我们反思整数教学，孩子第一次对数有了整体认识是什么时候？是父母或者老师教会孩子0～9，然后教孩子数出十几的数，再数二十几的或更大一点的数之后，孩子会突然自己数到100，稍加提示，还能知道1000以内数的排列规律。这个时候孩子对自然数（非负整数）的整体建构就有了第一次的整体把握。而后教材中安排了若干次大数的认识，细化和扩充、完善了对自然数范围内数域的若干问题的认识。数数成为了体会一类数的累计规则的最常见、最有效的学习方式。但是分数教学中我们几乎摒弃了这个最有力的“武器”。

基于这样的思考，我们以五年级分数的意义教学为契机，尝试了一次关于分数的数数教学。课中就如何数数、如何突破其中的若干教学难点作了相应的教学尝试。

三、教学实践

片段一：

老师在黑板上手绘3个圆圈（如图1所示），同时解释：由于是手绘，大小形状一定是有区别的，老师的本意是画一模一样的圆，大家就当作是完全一样的圆好了。然后提问：你们能在我画的图里找到1吗？3

图1

图2

图3

图4

师：很好，只要每一片都是等大的，这是关键对吧？那我将每一片都变成对应的圆形（如图4所示），现在能看到吗？生2：明白了！每一个圆都是这一堆圆的。

师：很厉害！我们不再需要考虑是否分割，只要能找到等量的一份又一份就能找到。那再来看看这幅图（如图5所示）里有吗？

图5

图6

图7

学生答能看到，老师请一生在黑板上画一画，让大家能看得更清楚。生画图如图6所示。

学生表示看不到。老师请一个女生上台，拿出3根粉笔交给女生展示，抽出其中的1根问道：这根粉笔是这个同学手里粉笔的几分之几？生3：。

老师放回这根粉笔，抽出第二根继续问：这根粉笔是这个同学手里粉笔的几分之几？

生4:。

老师用手提电脑的屏幕遮挡住学生和老师的手，然后去掉1根粉笔继续问：这根粉笔是这个同学手里粉笔的几分之几？生5：。

老师同时把学生手里的3根粉笔和自己手中的粉笔都举高再问：我这根粉笔是这个同学手里粉笔的几分之几？生6：。

图8

生7：甲的圆圈数是乙的圆圈数的。

师：说得很好！那么乙的圆圈数与甲的圆圈数有什么关系？

生8：乙的圆圈数是甲的圆圈数的3倍。

师：很好！看来倍数关系和我们学的分数也是有联系的，只要每一份的大小一样，它们之间的关系就能用分数和倍数表示。

教学意图：这一部分的教学设计将分数意义进行了倍率关系的沟通。强调平均分的含义是每一份的均等，而不是切分的过程。将单位“1”的强调转移到分数单位（一份）的认识上。这样一来，确立了一份（一倍）的标准，分数（倍数）就有了产生的可能。这样的一份在分数里被称为分数单位，分数单位的认识是数数的前提。任何一类数的累积都是有前提的，分数也必须由分数单位按照数的规则进行累积才能成为一类数。这部分教学是一个数数的预备动作，同时也是在分数意义教学上实现倍率关系的沟通。

片段二：

师：分数和整数一样都是数，都能应用到我们的生活实际当中。那你们现在帮我解决一个实际问题吧。（将一根长3.8米的塑料水管放置在讲台上）给你一根尺子，你能帮我把这根水管截成1米1米的长度吗？

一生上台用米尺量出1米长的水管，老师按照预先截好的缺口将1米的水管截下。

师：再请一个同学帮我截第二根。

另一生上来，并索要米尺，老师不给。学生索要刚截好的1米长水管。老师帮忙截下第二根1米长的水管。

师：他用这根刚截好的水管截第二根，这个做法好吗？

生（表示支持）：第一根水管已经是1米了，可以用它当尺子用。

师：是的，他的做法不但好，而且这在数学里也很高级。这个用来打样的水管我们在数学里叫做“标准”。（板书：标准）

老师按照学生的截取方法截下第三根1米长的水管。

师：好了，我们一起数数有多少米长吧。1米，2米，3米。孩子们，刚才我们拿来做标准的这个1米的“1”，就是这些整数的计数单位（板书：计数单位），计数单位就是计数时的标准。有了1，才会数得出2、3、4……

师：现在我们这还剩下一节边角料，很显然已经不能截成1米1米的了，为了不浪费，我们可以怎么截取？

生1：截成1分米一段的。

生2：截成10厘米一段的。

师：还可以用小数和分数表示为多少米？

生3：0.1米或者米。

师：那请一个同学上台来截一下吧。

老师协助学生截下数根0.1米长的水管，并且数出0.1米，0.2米，0.3米，0.4米……

师：这个时候0.1米就是我们截取的标准，也就是我们数数的计数单位。若是我们想继续分割剩下的这节更小的边角料，你们会怎么办？

生4：用厘米、毫米来截。

师：很好，我们也可以表示为0.01米，0.001米，等等。孩子们，人类是很聪明的，在度量时遇到原来的单位不能计量的时候，我们往往有两个方式来解决：一是改变度量的单位，二是改变计数单位。现在有一个真正难的问题需要大家帮助我解决，哪位同学愿意来尝试？（请两个孩子上台）请帮我截出0.3米。（板书：0.3米）

孩子们迅速用米尺找出了相应长度，准备截取。

师：别着急，还要多一点。（板书：0.33米）

孩子们又迅速地找到了相应长度，准备截取。

师：别着急，别着急，还要多一点。（板书：0.333米）

孩子们有些迟疑，因为米尺上没有毫米的刻度。

师：其实我是想要截出0.33333……米长的水管。（板书：0.33333……米）

台上的孩子开始冥思苦想，下面的孩子开始议论，有孩子说不能截出来。

师：孩子们，这个长度确实难以用米尺测量，哪怕是给你一根更加精确的尺子，也难以完成任务。其实这根尺子是这样来的：我将1米平均分成3份（板书：1÷3=_____米），用计算器一算，结果就是0.333……米。我那个计算器最多显示15位数，实际上这个数小数部分的3有无穷多个，我们把这种小数叫做无限循环小数。这个数是一个无法通过测量得到的小数。但是，你们知道1米被平均分成3份，每1份是多少米吗？生：米。

老师拿出三种颜色的橡皮圈，简单套拴成一条橡皮筋并拉伸，交给两个孩子。孩子通过拉伸橡皮筋至水管等长，找到米处，将米长的水管截下。

师：他们做得很棒，其实通过增加或减少橡皮圈的个数，我们还能找到其他分母的分数。现在我们截好了一个分数——米，用这个标准我们截出下面的长度，大家一起数数。

师：你们有些担心是吗？数起来有些不踏实？1 3米就是30多厘米，米是多少？米是多少？再加1个米有多长了，比1米多吧，米这个数用对了！现在心里踏实了吧！好，我们来数一遍：、、、米是多长？

生5：米是10米长。

生6：米是20米还多30多厘米。

师：说得很对！其实数学里存在这样的分子比分母大的分数，我们称之为假分数。但并非这些分数不真实，而是它确实和原来的分数不太一样。那好吧，谁来帮我解释一下个月饼是多少？

生7：个月饼是1个月饼还多一小块。

师：月饼不是被分成了3块吗？如何取出4块来了？

生8：1个月饼取完了，再取了第二个月饼的一部分，也就是个。

教学意图：这一部分的教学是数分数的开始，力图解决以下两个问题。

第一个是分数单位。整体认识任何一类数时，计数单位这个概念的教学总是一个难以处理的问题。本节课从整数的数数开始，到小数的数数，再到分数的数数，利用类似的问题情境告诉孩子们什么是度量的标准。这个标准其实在计数系统里就是计数单位。通过问题情境的类比体验，孩子会觉得分数中的数数就像自然数和小数一样自然。至于什么是分数单位，那就只是一个统一累计的标准而已。

我们认为，橡皮筋这个学具是一个非常经典的分数模型的原型。橡皮筋的原型有线段模型的特点，其伸缩性对不同的单位“1”有了不言而喻的直观诠释。后面的教学环节有橡皮筋这个原型的数学提炼模型：可以缩放的线段模型。这个模型是个全新的更接近分数本质的创造。

片段三：

师：孩子们，请看屏幕（如图9所示），老师这里有一根带箭头的线，线上已经标上了起点，还定好了一段线段长是“1”。请你们帮我找一找在哪。

图9

老师在数轴下面的分格刻度线上截取3整格，通过橡皮筋的拉伸与缩放，将数轴上的单位“1”等分成3份。再请孩子指出所在的点并标示。

学生表达不一，有的认为可以，有的认为不可以。

生1：。

师：下一个点呢？

生2：。

生3：就等于1。

师：这个不是已经标好了“1”吗？

老师一直未示意停止数数，但是学生慢慢停止了。

师：怎么了？你们怎么停止数数了？

生（笑）：这是数不完的，后面有无穷多个数。

师（竖起大拇指）：不错，像整数一样，分数也是数不完的。那你们能告诉我是多大吗？

生4：是3还多。

生5：是100。

生6：600是200。

3

师：他们说得都很好。在三分之几的这条数轴上，我们可以标示出三分之几，这里面其实包含所有整数。三分之几我们会在数轴上标示了，那四分之几呢？谁来帮我找找怎么标示？

师：接下来四分之几的其他分数怎么标示就很简单了吧。老师这里还有一些标示其他分数的数轴，（课件出示图10）大家认真看看这些分数数轴，是不是感觉数越来越密，分数单位越来小啊？假如我们继续这样将分母扩大，那在数轴上标示出来的分数是不是会更加密集？事实上，只要你的分母足够大，分数单位就会足够小，那在数轴上标示出来的分数就会越来越密。大家能想象得出吗？

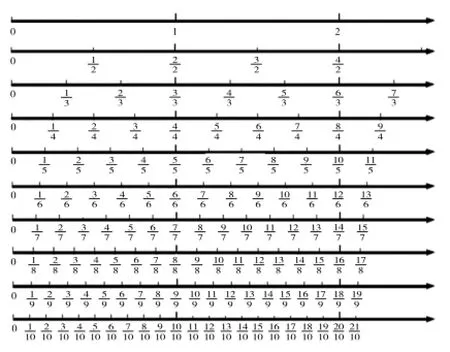
图10

师：好了，我现在把三分之几的数轴和六分之几的数轴（如图11所示）留下了，大家仔细对比一下，看看有什么发现。

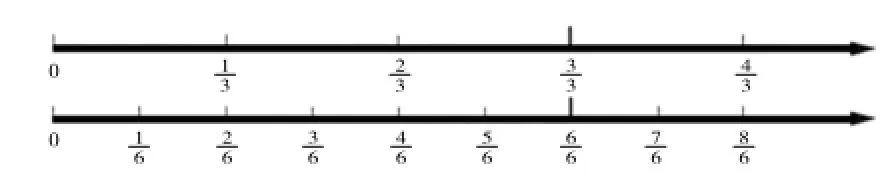
图11

生7：有一些点是公共的，比如和。

师：很好，那我们把两条数轴合并成一条（如图12所示），大家再观察。请问和谁会大一些？

图12

生8：会大一些，因为它在1的后面。

6

生8：。

师：这个你都知道，真不错。最后我们讨论一个问题。请看：我手里有3根橡皮筋。其中一根可以用什么分数表示，另外两根呢？

生9：分别用、表示。

生10：2倍。

师：那反过来怎么说呢？

生11：是的。

师：你的回答太完美了！这节课大家的表现太棒了，下课！

教学意图：笔者认为，只有将一类数“站”到数轴上，才能说在数的概念上取得了实质性的进展。所以这个环节中，当孩子们找到所对应的线段长之后，从0开始增长，找到等对应点就变得非常规范、自然。孩子在取的时候是在的基础上再增加一个的线段长，这说明孩子们已经淡化了分数意义里的等分过程，在做有关数的有序累积，这是一个有效的教学体现。

四、不得不说的后话

1.关于橡皮筋这个分数模型的原型

我们之前的分数教学中，分数模型大多采用面积模型。张奠宙教授曾经非常精辟地论述了分数模型：在数直线上对分数作几何解释是非常重要的。这是一个半抽象的模型。线段模型是圆模型和其他平面模型的再抽象，可以充当分数的“份数模型”向“除法的商”定义过渡的几何载体。用线段的长度表示分数的大小，无论大饼、蛋糕有多大，这里的单位都是1。对于切下来的1份或2份，学生的脑子里不再局限地呈现1或2，而是一个新的数。这样表示的好处有很多。首先，它的单位是抽象的“1”。虽与圆形、三角形相比要抽象，但仍然是几何直观，可以帮助学生感知分数的含义。其次，这是数轴的雏形，早在学习自然数的时候，已经用过这样的表示方法。再次，通过操作可以看到分数是填在自然数之间的新数，位置在两个相邻的自然数之间，并和分数大小比较、约分、通分以及运算相呼应。

2.关于分数上数轴

分数上数轴这个教学环节，有几个教学细节值得跟大家分享。

一是将同分母的分数完整地标示到数轴上。这个教学动作与之前有教师将不同分母的分数统一标示在同一条数轴上让孩子观察体验是有区别的。后者实际上造成了学生的认知困难，他们会认为分数是一类极其混乱、难以判断大小和次序的数。而按同分母的分类标准将分数标示在数轴上，孩子们通过数数认知到了一列又一列分数的有序，能直接感知分数的大小，对分数的数的认知形成了统一准确的表象。这节课在试教阶段甚至有孩子有这样的体会：分数是一类比整数大的数！孩子的意思是整数可以看作分母都是1的一列分数，整数是包含在分数范畴里的一类数而已。这是多么深刻的认识！这个教学动作实际上是异分母分数上数轴之前的一个必要和有效的教学动作分解，是让学生建立完整的分数的数认识的一个非常关键的构建过程。

二是分数上数轴有一个小小的技术难题。很多教师直接把分数墙进行压缩，成为一根数轴，用这个教学动作完成分数上数轴的意图。这样做不能回答一个问题，在数轴上，数是与数轴上的点集形成一一对应的。如何才能实现线段的线长到数轴上的点集的转化？要完成这个转化的过程，我们必须知道数轴建立的原则，数轴是一根规定了起点、方向和单位长度的直线（数轴的三要素）。所以我们可以看作所有数都是从原点0开始增长相应长度之后所到的点表示为该点所对应的数。

这节尝试的课堂里容量非常大。比如，分数意义的沟通就可以好好上一到两个课时；关于自然数、小数、分数的比较认识，用一整节课来让学生感受估计都会觉得有些匆忙；数轴这个话题也有很多有趣的游戏可以和学生一起玩。但是这并非一节常规课，而是一堂教研课，想以“数一数”分数的形式带领孩子体验分数这一类数。数数并不是一件简单的事情。为了能数得起来，数得顺利，数出感觉，这堂课在这三个方面都必须做到位。数数对整个分数教学单元来说，只是其中一个非常小的教学动作。本文尝试从这个角度讲清如何从数的概念的高度落实到具体的教学环节，以达抛砖引玉的意愿。

分数的教学是很多有识之士研究的对象，每一个研究者的成果都是见仁见智的。我们之前的分数教学对分数这一类数的特殊属性强调过多，而对它有关数的共同属性却认识不够，导致学生对分数的认识产生割裂，学习分数的难度加大。把分数当作一类数来教，希望能成为研究这一类教学问题的基本共识，这是原有分数教学中一个需要调整的基本问题，也应该成为今后此类问题研究的一个核心和方向。分数教学是时候回归数的本质进行审视了。

分数教学的研究是个系统工程，我们需要在数的教学的大前提下做好分数教学整体编排的重新建构，在这个建构下再落实知识点突破的细化。比如从分数意义的初步认识到多种意义的沟通，从分数的认识到小数、自然数的比较学习，从分数比较大小到四则运算再到解决问题。这些都需要我们做更加精细、更加科学的实验和论证。

由于自身素养和认识水平的问题，我们的研究中难免存在问题，希望得到大家的批评与指正。但是我们意图通过这种有限发声吸引更多有关分数研究的新的声音，渴望看到更有力的研究呈现，期待分数的教学出现更好、更新的面貌。

（执笔：汪松浩、徐旺、李闯）