基于改进教与学优化算法的配电网重构

邱骁奇，胡志坚



基于改进教与学优化算法的配电网重构

邱骁奇，胡志坚

(武汉大学电气工程学院，湖北 武汉 430072)

正常运行工况下的配电网重构能降低配电网损耗。近年来新兴的教与学算法具有自有参数少、简单易懂、收敛迅速等优点，十分适合多目标、多约束的配电网重构优化问题求解。以网损最小和开关操作次数为目标，并考虑运行经济成本，将教与学算法引入到配电网优化重构中，对基本教与学算法中的教学因子进行了自适应改进，给出了算法的编码策略、迭代过程中“学生”信息的修改原则。PG&E 69节点系统以及一个实际城区配电网的优化重构仿真结果表明所提改进算法的有效性。

配电网重构；网络化简；改进教与学算法；教学因子

0 引言

配电网最显著的特点是闭环设计、开环运行，网络中装配了数量众多的开关，其中分段开关占绝大多数而联络开关数量很少。正常运行时，闭合分段开关而断开联络开关。配电网重构的本质即通过改变网络中开关的开闭状态从而改变网络拓扑，实现网络各运行参数的优化，最终达到降低配电网损耗这一最重要的目的[1-3]。此外，配电网重构还能实现平衡负荷、消除系统过载及提高供电电压质量[4]等目标。

配电网重构是一个复杂的非线性组合优化问题，其具有多目标、多组合、多约束的特点，优化的目的就是要在所有可行的开关组合中找到一组最优解使得目标函数值最优。目前，配电网重构的方法基本可以分为以下几类：1) 传统的数学优化技术算法[5-6]，此类方法在对配电网的重构时引入了数学优化法，其有着很好的数学基础。但网络规模较大时，算法耗时长、难以得到最优解。2) 最优流模式算法[7]，用潮流计算优化问题来替代开关组合问题，算法简单，易收敛；但计算过程复杂，重构结果可能出现孤立节点。3) 支路交换算法[8]，引入了启发式规则对开关组合进行筛选，通过估算开关操作前后的网损变化迅速得到最优的开关组合。但其单次优化结果易陷于局部最优，且原始网络的拓扑会对重构结果产生较大影响。4) 人工智能算法，如遗传算法[9-10]、蚁群算法、人工神经网络算法[11]、粒子群优化算法[12-14]等。近年来，人工智能算法因其能保证得到全局最优解而被广泛应用于配电网重构，但也存在着自身参数较多，参数的设置和组合会对结果产生直接的影响等缺陷；同时，还存在全局搜索性和计算时间耗费的矛盾。因此，上述智能算法在配电网重构问题上的应用效果并非很理想。

教与学算法[15-17](Teaching-Learning-Based Opt- imization，TLBO)是Rao等人于2011年提出的一种新的群体智能优化算法，它实现了课堂上教师给学生的教学过程和学生的学习过程的模拟，学生学习成绩的提升是通过教师的“教”和学生之间的相互“学习”两个阶段来实现的。教与学算法与上述的人工智能算法相比，其具有简单易懂、算法自有参数少、求解精准、收敛迅速且收敛性能好等优点。本文将教与学算法引入到配电网重构问题中，取得了较好的效果。

1 配电网重构数学模型

正常运行时进行配电网重构一般以有功功率损耗最小为研究目标。但仅以有功损耗最小的重构研究中，往往没有考虑开关的操作次数。一方面，开关操作会影响系统的安全性和稳定性；此外，过多的开关操作也会增加运行成本。因此需要考虑开关操作次数，此时的重构目标函数为式(3)。

以网损最小为目标的配电网优化重构目标函数ploss可表示为

式中：为网络中元件总数；c表示元件的状态，0代表停运，1代表投运；Pin和Pout表示元件注入有功和输出有功。

开关操作次数的计算式sc为

式中：为网络中可操作开关的总数；sc为重构前第个开关的状态；scr为重构后第个开关的状态，0表示打开，1表示闭合。

重构优化的研究目标函数(综合损耗)为

式中，、分别表示开关操作次数和网损对于综合损耗的权重系数。

配电网重构必须满足的约束条件为

式中，S、Smax分别表示节点的视在功率和最大允许功率。

式中，U、Umax及Umin分别表示节点的实际电压值和电压的最大限值、最小限值。

式中：g代表重构后第个网络结构；为所有可行的辐射状网络结构集合。

2 配电网拓扑结构简化模型

配电网的拓扑结构并不复杂，从实际的连接关系中抽象出其本质就是由节点和支路相互连接所形成的辐射状网络，而且还具有闭环设计、开环运行的特点。将实际的配电网抽象成点与线组成的图对配电网重构十分重要，其遵循以下的模型建立规则：用图的各边表示原网络的各开关，而图的节点则表示原网络中的各设备。将配电网的实际接线图按照上述规则抽象为简单的拓扑图，就把配电网拓扑转化成了一个点和线组成的图的问题[18]，从而使实际配电网的拓扑结构的数学意义更为明确，研究起来更为简单。

智能算法初始解的产生随机性很强，在初始化及迭代过程中会出现大量的不可行解。不可行解的含义是指经过解码还原得到的备选方案的拓扑结构无法满足网络拓扑约束条件，即备选网络中出现了“孤岛”或“环网”。不可行解的出现会使算法的搜索效率极大降低，故尽量避免不可行解的产生是十分重要的。除此之外，实际配电网规模庞大，节点、支路数众多，待优化变量数很多，会造成应用智能算法时编码难度很大，因此对原有配电网络进行化简是必要的。

本文将图论中的同胚图理论[19]与配电网自身的特点结合，对配电网拓扑进行化简。简化原则如下：

1) 编码时，只选取能形成环路的支路(开关)开闭状态当作优化变量，而忽略那些不在回路中的节点(电源节点除外)和支路(连接电源节点的支路除外)。

2) 删除网络中出线数为2的节点，将其所关联的支路合并成一条简化支路，简化支路实质上包含了原有网络中的数条支路。

上述化简原则也即网络化简的两个步骤：首先删去环路以外的节点、支路；然后再对支路进行处理，形成简化支路。

以IEEE 16节点配电网为例，说明配电网化简的基本过程，如图1。

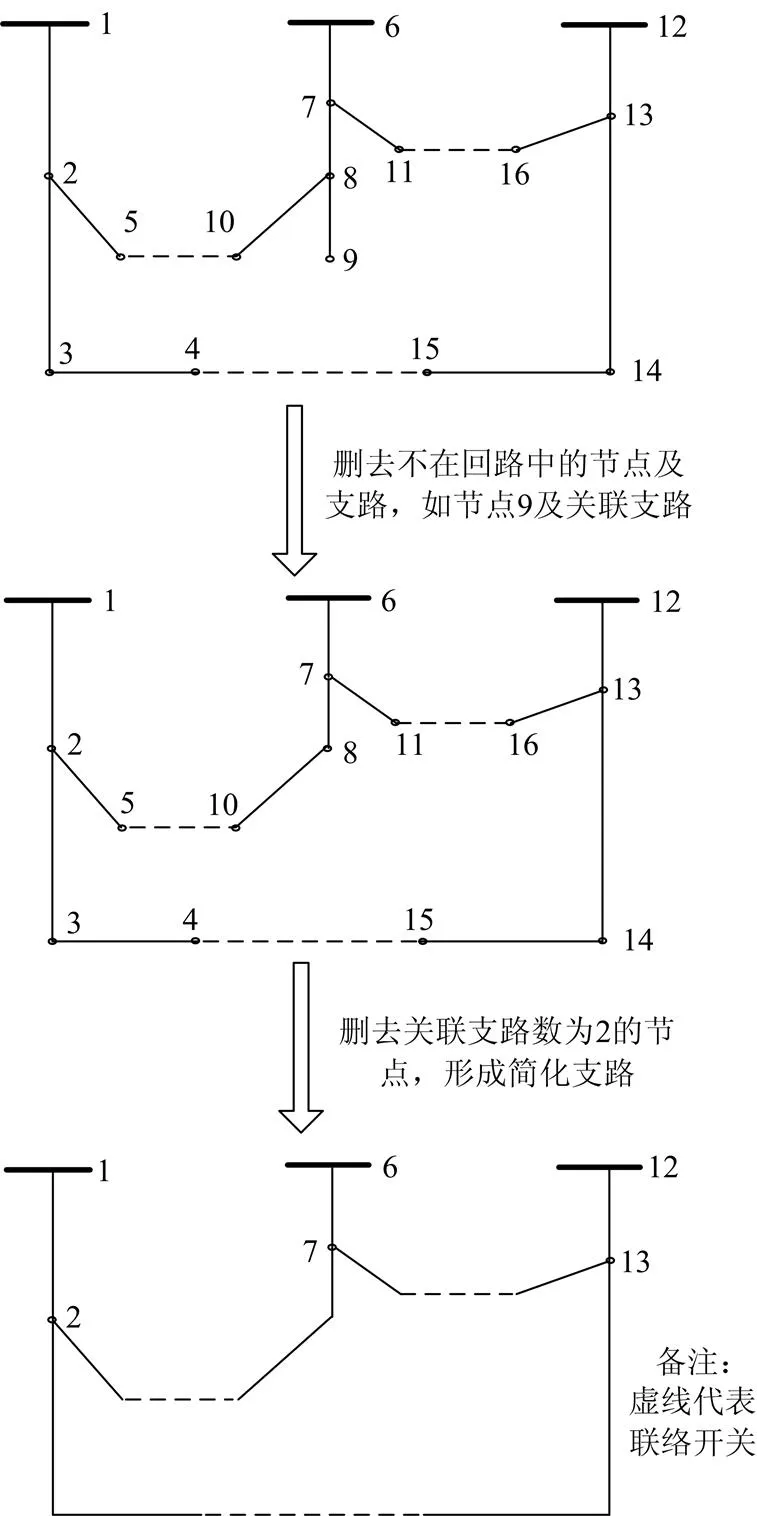
图1配电网简化过程

网络化简后与化简前相比，节点数仅为6个，支路数仅为7条。经过化简处理后待优化变量大大减少，不可行解的数量也大大减少产生，从而极大地提高了算法搜索效率。

3 教与学算法配电网重构

3.1 教与学算法

教与学算法(Teaching-Learning-Based Optimi- zation，TLBO)模拟实际教学过程中的“教”与“学”模式，其具有自有参数少、无需进行参数设定[20]等优点，因此非常适用于求解非线性、强约束的多目标优化问题。

TLBO算法中，班级(class)(搜索空间)由学生X(1, 2,,)组成，学生X的各科成绩(X,1,X,2,, X)代表各决策变量，从班级中选出成绩最优的学生best担任教师Teacher。其中，为总的学生数，为课程科目数(决策变量个数)。

TLBO算法的基本步骤可以分为以下几步：

1) 搜索空间初始化。为所有班级中的“学生”初始化

2)“教”阶段

在“教”阶段结束之后，比较“学生”在此阶段前后各科的成绩，若更优，则更新“学生”信息。

3)“学”阶段

从全部学生中随机抽取一个学生作为学习对象X(≠)，此阶段学生成绩的提升是通过学生之间的相互学习来完成。对于求解最小值问题，“学”阶段可以描述为

式中：Xold、Xnew分别表示学生X在“学”阶段学习前后的表现；r是0到1之间的随机数。

在“学”阶段结束之后，比较“学生”在此阶段前后各科的成绩，若更优，则更新“学生”信息。

4) 若满足迭代结束条件，则结束优化；否则转到步骤2)继续迭代。

3.2 编码策略

配电网正常运行必须满足辐射状，当任意一个联络开关闭合时，配电网将形成一个回路。为满足配电网的运行约束条件，就必须断开回路中的一个开关。配电网中支路数量众多，要进行优化计算就必须首先对支路进行合理的编码。本文采用基于回路的十进制编码策略[21]。采用这种编码方式能缩小搜索空间的范围，加快寻优速度，易于找到最优解。

基于回路的十进制编码策略，其将配电网中所有的开关闭合时形成的网孔定义为回路，按照从小到大的次序对各个回路中的全部开关取从1到该回路总的开关数的整数依次进行编码，并称其为回路编号。根据被选为联络开关的开关所对应的回路编号组成学生。一个回路中必须但也只能包含一个联络开关，因此学生信息中的科目数(决策变量数)为回路数，也即联络开关的总数。

以图2中的IEEE 33标准网络中回路1为例，说明配电网重构编码策略。

表1为图2中回路1的开关编码。其余回路的编码跟回路1的编码策略完全一致，在此不再赘述。

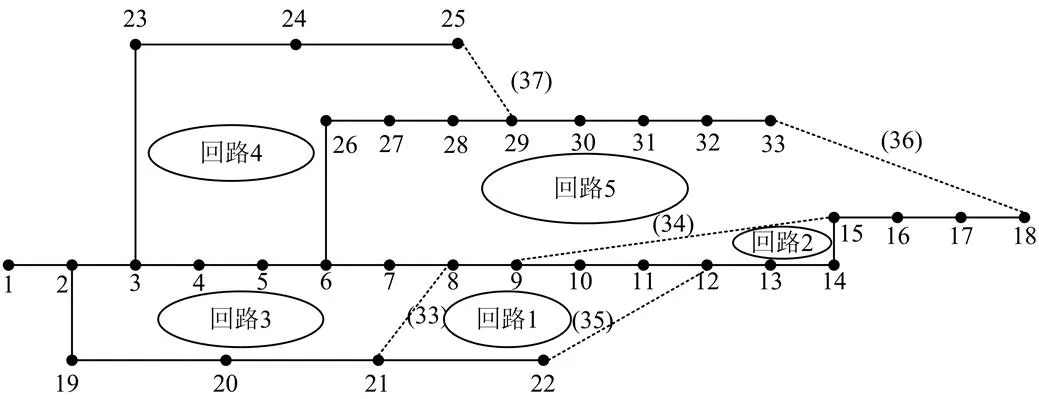
图2 IEEE 33节点标准网络

表1支路编码

Table 1 Coding of branches

对于IEEE 33标准网络，支路总数为37，每条支路都有开关，不考虑处在环路外的支路1上的开关，状态可改变的开关数为36。采用基于环路的十进制编码，科目数为5，搜索空间容量为。如若采用二进制编码，科目数则为36，搜索空间容量则为236。显然，采用基于环路的十进制编码能极大地缩小搜索范围，显著提高算法搜索效率。

3.3 教学因子自适应改进

基本教与学算法中教学因子表示“学生”对“教师”教学的学习效果的优劣，教学因子的取值一般取整数1或2。这样的取值表示学习的效果只有两种极端的情况，其一是对“教师”的教学全盘否定，此时的=1；其二是对“教师”的教学全盘接受，此时的=2。但在实际的学习过程中，每个“学生”的学习能力存在差异，上述的取值情况并不能反映出“学生”学习效果的真实性，因此，提出一种自适应的教学因子对原有的教与学算法进行改进是十分必要的。

在TLBO 算法中，教学因子是“成绩”平均值变化程度的决定性因素，会对算法结果产生较大的影响。较大的能实现算法的快速搜索，但会降低搜索能力；相反地，较小的改善了搜索的搜索效果，但会牺牲算法的收敛速度。

实际学习过程中，学生依据自己的学习能力向教师学习，“教”阶段前期，“学生”与“教师”之间的水平差异明显，学生的学习效果较好；在“教”阶段后期，“学生”与“教师”的水平差异逐渐缩小，学习成绩提升速度变慢。

本文将教学因子对算法的影响与实际的学习过程相结合，提出在迭代过程中自适应改变教学因子的值，将改进后的TLBO算法称为改进教与学算法(Improved Teaching-Learning-Based Optimization，ITLBO)。自适应教学因子表示为

式中：max、min分别表示教学因子的最大值和最小值；为总的迭代次数；为当前的迭代次数。

根据上述教学因子改进方法将式(9)修正为

3.4 教与学配电网重构流程

基于改进教与学优化算法的配电网重构流程如图3所示。

4 算例分析

本文选取PG&E 69节点标准系统和某市实际配电网络这两个算例进行仿真分析。

4.1 标准算例分析

本文所选取的标准算例为美国PG&E 69节点配电网，网络参数见文献[12]。取基准容量为100 MVA，基准电压为12.66 kV。将网络化简后形成五个回路，则“学生”所学科目数为5。正常运行条件下，权重系数设为=0，=1；表示只考虑网络有功损耗。

对此标准算例，分别采用TLBO、ITLBO和粒子群优化(Particle Swarm Optimization, PSO)算法对其进行配电网重构优化。优化结果如表2所示。三种算法中的种群数均设为50个，均迭代50次。

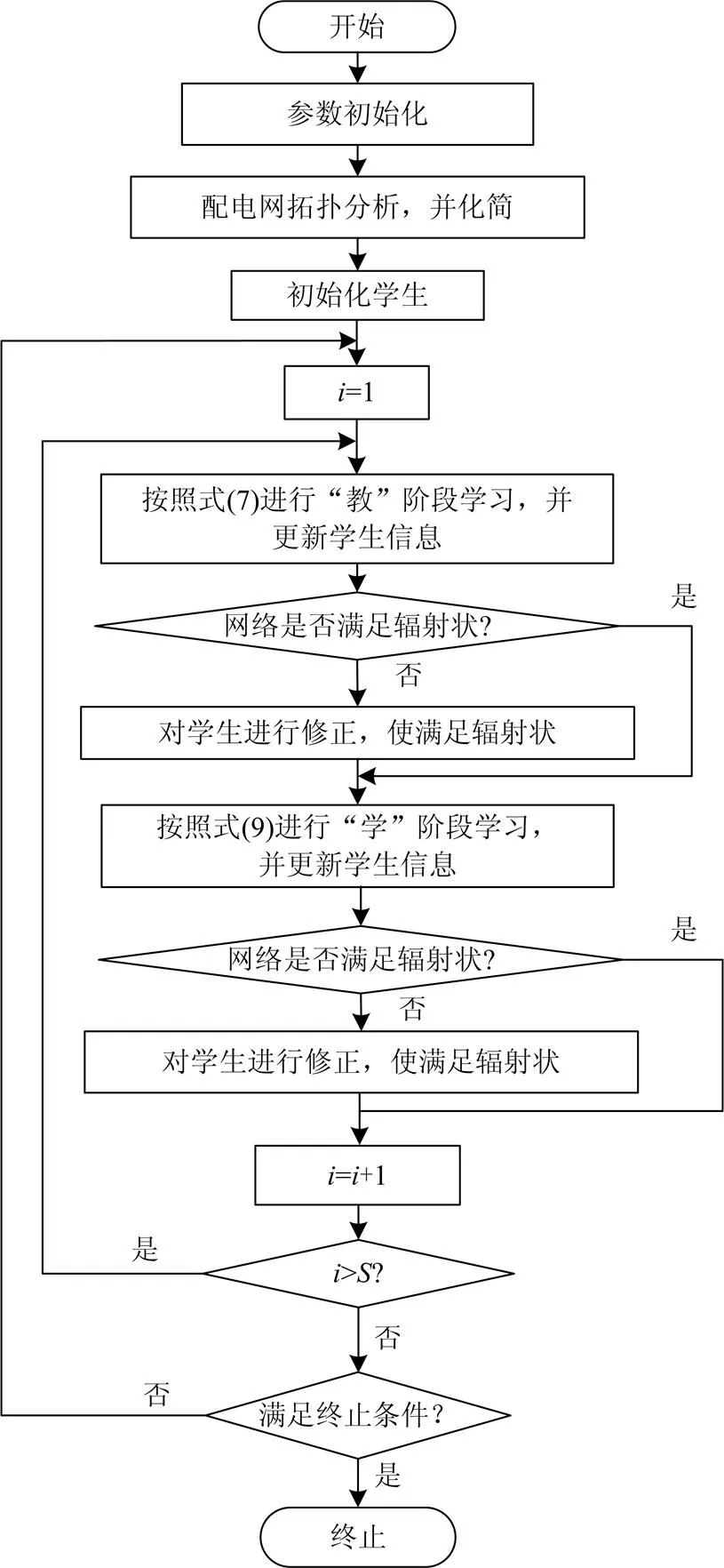
图3 基于改进教与学优化算法的配电网重构流程图

表2 PG&E 69节点配电网重构结果比较

由表2可以看出：采用上述三种算法对配电网进行优化重构后，网络的有功损耗相比于原网络的有功损耗大幅降低，网络中节点的最低电压得到大幅提升，且ITLBO的优化效果更优于TLBO、PSO。

分别用TLBO、ITLBO和PSO算法对PG&E 69节点配电网进行重构优化的迭代过程如图4所示。

图4 PG&E 69节点配电网重构迭代过程

从图4可以看出：ITLBO和PSO比TLBO迭代结果的网损值更小；ITLBO算法的收敛更迅速，收敛过程更平稳。

分别采用TLBO和ITLBO对PG&E 69标准算例进行重构优化，重构前后系统中各节点电压的标幺值分别如图5所示。

图5 PG&E 69节点配电网重构前后节点电压

由表2以及图5可以看出：采用TLBO和ITLBO对配电网进行重构优化后，系统中节点的最低电压得到了提升，且绝大多数节点的电压都得到了提高，配电网供电质量得到显著提升。

分别采用TLBO、ITLBO和PSO算法对标准算例进行20次独立运算，算法每次运算的迭代次数都设为50次，比较结果如表3所示。

表3PG&E 69节点系统算法优化性能比较

Table 3 Comparison of the optimization performance of the algorithm of PG&E 69

由表3可以看出：当测试的硬件条件和参数条件均相同时，ITLBO最优解均优于TLBO与PSO算法；且ITLBO算法的稳定性最好。

4.2 实际配电网计算分析

本文的实际算例选自某市主城区配电网。配电网中共有153个节点、201条支路数。该系统中包含四个电压等级，分别为220 kV、110 kV、35kV和10kV，总负荷为523.29 MW+105.33 Mvar。分段开关和联络开关主要分布在10kV线路上，数目分别为65个和46个，但联络开关中有5个不参与重构，故可操作开关数为41个。

由于重构时需要操作的联络开关和分段开关都是与电压等级为10kV的母线相连，故在进行重构优化时选取10kV为基准电压，将各电压等级下的负荷归算至基准电压下。系统基准容量设为1 000MVA。算法各参数设置如下：“学生”数(种群数)设为100个，科目数(变量数)设为41，最大迭代次数设为100次。

实际算例中联络开关数目较多，大量的开关操作会影响系统的安全性和稳定性，因此本节在考虑降低网损的同时，还考虑了开关操作次数的影响。本节考虑了开关操作的经济效益，以综合损耗为目标，按式(3)进行优化重构。此时的重构优化，目标函数式(3)中开关操作次数和有功损耗的设置权重系数设为=0.01，=0.99。

重构前，断开网络中所有的联络开关，计算出系统网损为4.111 3 MW。在系统正常运行条件下，对算例分别采用TLBO、ITLBO和PSO算法进行重构优化。假设实时电费为0.5 $/kWh，开关操作一次的等价损失费用为$20[22]。计算重构一小时内网络的综合损耗如表4所示，表中还给出了仅考虑网损最小的情况(*)。

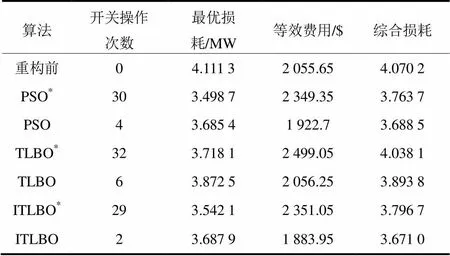
表4 重构结果比较(a=0.01, b=0.99)

由表6可以看出：考虑开关操作次数情况下进行重构优化，配电网的综合损耗较大幅度地降低；1小时内，等效费用也得到降低。三种算法中，ITLBO和PSO算法的优化效果优于TLBO，且采用ITLBO算法优化后综合损耗与等效费用最低。本文所提的综合损耗考虑了开关操作次数，与仅考虑网损时相比，虽然重构结果中网损增大，但开关操作次数少，能有效提高系统运行安全性和稳定性并减少运行成本，综合效益更优，实现最优经济运行。

采用TLBO、ITLBO和PSO算法对实际算例进行重构优化的迭代过程分别如图6~图8所示。

图6实际配电网算例重构网损迭代过程(a=0.01, b=0.99)

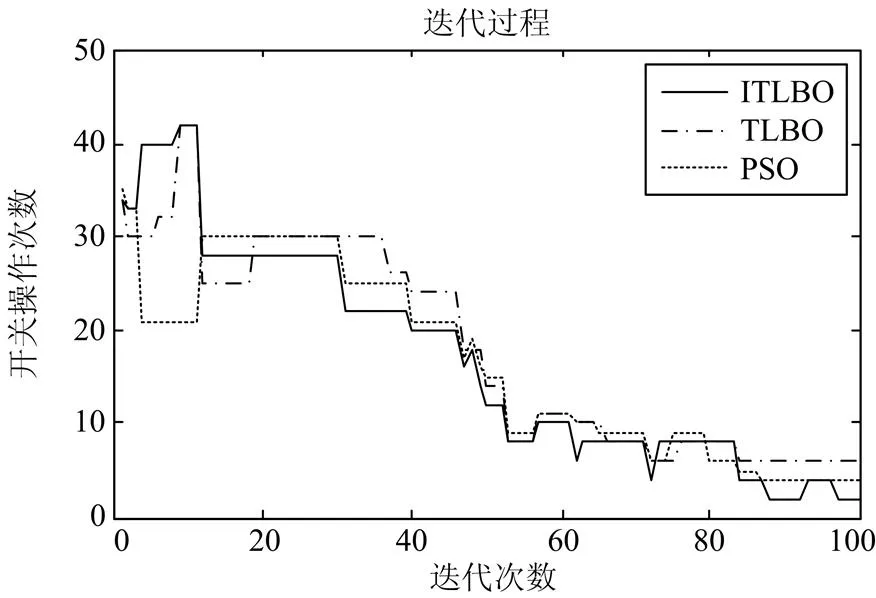
图7开关操作次数迭代过程

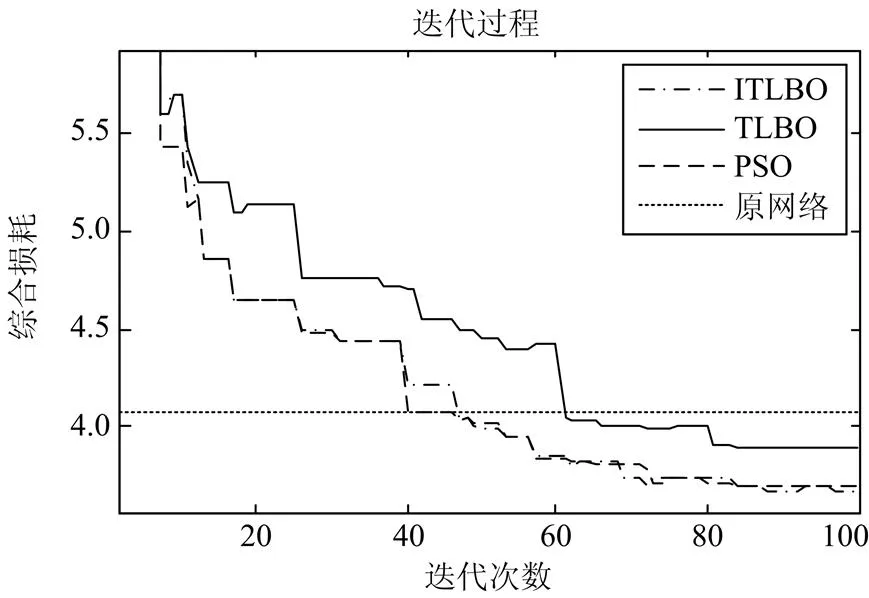
图8实际配电网算例重构综合损耗迭代过程(a=0.01, b=0.99)

5 结论

本文将教学因子进行自适应改进后的教与学优化算法引入到配电网重构问题中，通过对标准算例和实际配电网的重构进行仿真，并与粒子群算法进行对比分析，得到如下结论：

(1) 采用ITLBO、TLBO和PSO算法对配电网进行重构优化，均能达到降低网损的目标；且ITLBO与TLBO相比，求解出的系统网损更小；与PSO算法相比，收敛更加迅速，稳定性更强。

(2) 采用ITLBO、TLBO和PSO算法对配电网进行多目标重构优化，综合损耗不仅低于原网络，而且还优于单目标优化结果；系统运行成本更低，综合效益更好，且采用ITLBO算法后系统的综合损耗与等效费用均更低。

[1] 陈芳, 张利, 韩学山, 等. 配电网线损概率评估及应用[J]. 电力系统保护与控制, 2014, 42(13): 39-44.

CHEN Fang, ZHANG Li, HAN Xueshan, et al. Line loss evaluation and application in distribution network[J]. Power System Protection and Control, 2014, 42(13): 39-44.

[2] 王璟, 金尧, 黄泽华, 等. 考虑间歇性电源不确定性的配电网经济效益风险评估[J]. 电器与能效管理技术, 2015(13): 14-18.

WANG Jing, JIN Yao, HUANG Zehua, et al. Risk assessment of distributed network integrated with intermittent energy[J]. Electrical & Energy Management Technology, 2015(13): 14-18.

[3] 颜庆国, 孟学阳, 崔玉, 等. 基于微电网与配电网互动的综合效益评估[J]. 电器与能效管理技术, 2014(21): 47-52.

YAN Qingguo, MENG Xueyang, CUI Yu, et al. Comprehensive benefit evaluation based on interaction of micro-grid and distribution network[J]. Electrical & Energy Management Technology, 2014(21): 47-52.

[4] BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(4): 1401-1407.

[5] MERLIN A, BASK H. Search for a minimal-loss operating spanning tree configuration in urban power distribution system[C] // Proc of 5th Power System Computation Conf, Cambridge (UK), 1975: 2-6.

[6] CHIANG-HSIAO D, RENEJEAN J. Optimal network reconfiguration distribution systems part I: a new formulations and a solution methodology[J]. IEEE Transactions on PWRD, 1990, 5(4): 1902-1909.

[7] SHIRMOHAMMADI D, WAYNE H H. Reconfiguration of electric distribution network for resistive line losses reduction[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1492-1498.

[8] CIVANLAR S, GRAINGER J J, YIN H, et al. Distribution feeder reconfiguration for loss reduction[J]. IEEE Transactions on Power Delivery, 1988, 3(3): 1217-1223.

[9] 李振坤, 刘俊, 杨帆, 等. 有源配电网的综合供电恢复及改进遗传算法[J]. 电力系统保护与控制, 2014, 42(17): 24-30.

LI Zhenkun, LIU Jun, YANG Fan, et al. Restoration of distribution network containing DG and a refined genetic algorithm[J]. Power System Protection and Control, 2014, 42(17): 24-30.

[10] 颜湘武, 段聪, 吕正, 等. 基于动态拓扑分析的遗传算法在配电网重构中的应用[J]. 电网技术, 2014, 38(6): 1639-1643.

YAN Xiangwu, DUAN Cong, LÜ Zheng, et al. Application of dynamic topological analysis based genetic algorithm in distribution network reconfiguration[J]. Power System Technology, 2014, 38(6): 1639-1643.

[11] 韩祯祥, 文福拴. 人工神经元网络在电力系统中应用的新进展(一) [J]. 电力系统自动化, 1993, 17(1): 53-59.

HAN Zhenxiang, WEN Fushuan. The new development of artificial neural networks application to power system[J]. Automation of Electric Power Systems, 1993, 17(1): 53-59.

[12] 卢志刚, 董玉香. 基于改进二进制粒子群算法的配电网故障恢复[J]. 电力系统自动化, 2006, 30(24): 39-43.

LU Zhigang, DONG Yuxiang. Distribution system restoration based on improved binary particle swarm optimization[J]. Automation of Electric Power Systems, 2006, 30(24): 39-43.

[13] 李振坤, 陈星莺, 余坤, 等. 配电网重构的混合粒子群算法[J]. 中国电机工程学报, 2008, 28(31): 35-41.

LI Zhenkun, CHEN Xingying, YU Kun, et al. Hybrid particle swarm optimization for distribution network reconfiguration[J]. Proceedings of the CSEE, 2008, 28(31): 35-41.

[14] 吕林, 罗绮, 刘俊勇, 等. 基于多种群分层粒子群优化的配电网络重构[J]. 电网技术, 2009, 39(19): 56-60.

LÜ Lin, LUO Qi, LIU Junyong, et al. Reconfiguration of distribution network based on hierarchical structure poly-particle swarm optimization[J]. Power System Technology, 2009, 39(19): 56-60.

[15] RAO R V, SAVASNI V J, VAKHARIA D P. Teaching- learning-based optimization: a novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011, 43(3): 303-315.

[16] RAO R V, SAVASNI V J, BALIC J. Teaching-learning- based optimization for unconstrained and constrained real parameter optimization problems[J]. Engineering Optimization, 2012, 44(2): 1447-1462.

[17] RAO R V, SAVASNI V J, VAKHARIA D P. Teaching- learning-based optimization: an optimization method for continuous non-linear large scale problems[J]. Information Sciences, 2012, 183(1): 1-15.

[18] 刘健, 程红丽, 毕鹏翔, 等. 配电网的简化模型[J]. 中国电机工程学报, 2001, 21(12): 77-82.

LIU Jian, CHENG Hongli, BI Pengxiang, et al. A simplified model for distribution system[J]. Proceedings of the CSEE, 2001, 21(12): 77-82.

[19] 郭志忠. 电力网络解析论[M]. 北京: 科学出版社, 2008: 1-13.

[20] 贺建波, 胡志坚, 刘宇凯. 大规模多目标水-火-风协调调度模型的建立及求解[J]. 电力系统保护与控制, 2015, 43(6): 1-7.

HE Jianbo, HU Zhijian, LIU Yukai. Establishment and solution of the large-scale multi-objective hydro-thermal- wind power coordination optimization dispatching model[J].Power System Protection and Control, 2015, 43(6): 1-7.

[21] 彭先胜. 基于粒子群算法的配电网络重构研究[D]. 西安: 西安理工大学, 2010.

PENG Xiansheng. The research of distribution network reconfiguration based on particle swarm optimization[D]. Xi’an: Xi’an University of Technology, 2010.

[22] 孙惠娟, 彭春华, 袁义生. 综合开关次数分析的配电网多目标动态重构[J]. 电力自动化设备, 2014, 34(9): 41-46.

SUN Huijuan, PENG Chunhua, YUAN Yisheng. Multi- objective dynamic distribution network reconfiguration considering switching frequency[J]. Electric Power Automation Equipment, 2014, 34(9): 41-46.

(编辑 葛艳娜)

Reconfiguration of distribution network based on improved teaching-learning-based optimization algorithm

QIU Xiaoqi, HU Zhijian

(School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

The reconfiguration of distribution network can reduce the loss of positive power in normal condition. There are many optimization algorithms for the reconfiguration of distribution network. As an emerging algorithm, Teaching-Learning-Based Optimization (TLBO) Algorithm has some advantages. For example, the algorithm has less algorithm-specific parameters, and is easy to understand and converge quickly. So TLBO is very suitable for the reconfiguration of distribution networks which is a multi-objective and multi-constraint problem. This paper chooses the minimization of the net loss and the switch operation times as the objectives, considers the costs of operations, and introduces TLBO into the research of distribution network reconfiguration. It elaborates on the coding strategy and the principle of modification of individual during iterations and self-adaptive modification of teaching factor in TLBO algorithm. The simulation results of PG&E 69 and a practical distribution network of a city validate the effectiveness of the improved TLBO proposed.

This work is supported by Research Fund for the Doctoral Program of Higher Education of China (No.20110141110032).

distribution network reconfiguration; network simplification; improved Teaching-Learning-Based Optimization; teaching factor

10.7667/PSPC151271

2015-07-22；

2015-09-19

邱骁奇( 1990-)，男，通信作者，硕士研究生，研究方向为配电网重构优化与故障恢复；E-mail: 770166368@ qq.com

胡志坚( 1969-)，男，博士，教授，博士生导师，研究方向为互联电力系统鲁棒协调控制、输电线路参数带电测量、智能电网。

高等学校博士学科点专项科研基金项目(20110141110032)